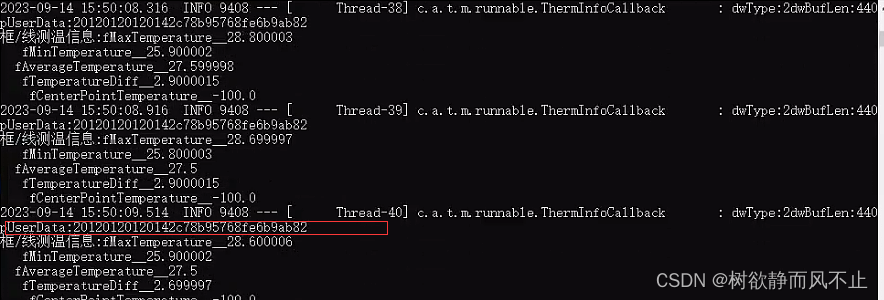
文章目录
- 1. 频率
- 2. 累计直方图
- 3. 取整
- 4. 得到对应关系
- 5. 累加对应关系,得出结果
- 6. 画出均衡化后的直方图
1. 频率
一般题目会给出各个灰度级的概率分布,如果没有给概率,而是给了频率,比如:
- 在 8x8 的图像中,0 出现了 8次,那么概率就是 8 / 64 = 1 / 8
- 以此类推可以求出所有的概率

2. 累计直方图
通过上面的图标,我们先计算出累计直方图:
- 0 的累计直方图 = 0 的概率
- 1 的累计直方图 = 0 的累计直方图 + 1 的概率
- 2 的累计直方图 = 1 的累计直方图 + 2 的概率
- 3 … 以此类推
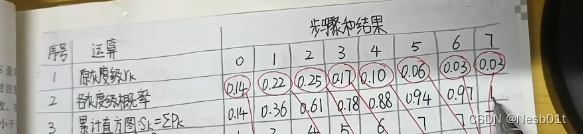
像这样,左边的加上面的即可

3. 取整
通过公式 (L - 1) x S,然后四舍五入取整:
- L 就是 8,因为从 0 ~ 7 有 8 个灰度级
- S(k) 就是我们上面计算出来的东西
- 举例,坐标 0 的结果 = 7 x 0.14 = 0.98,四舍五入是 1
- 举例,坐标 1 的结果 = 7 x 0.36 = 2.52,四舍五入是 3
- 以此类推…
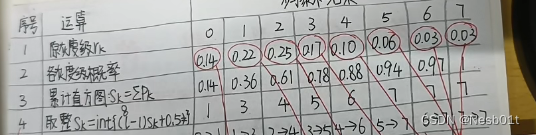
4. 得到对应关系
通过上面的取整,我们这样写来得到一一对应的关系:
- 0 指向 1
- 1 指向 3
- 2 指向 4
- 3 指向 5
- 4 指向 6
- 567 指向7
看图中的红色箭头作为示例:
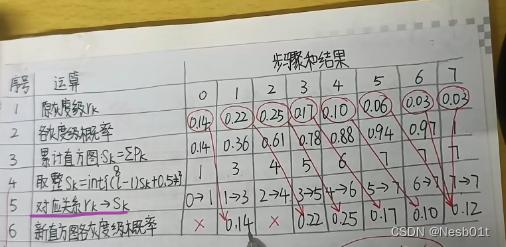
5. 累加对应关系,得出结果
可以看到 0 和 2 没有被指向,他们就没有了
- 由于 0 -> 1 所以 1 这里是 0.14
- 由于 567 -> 7 所以 7 这里是 0.06 + 0.03 + 0.03
计算结束后这就是结果:
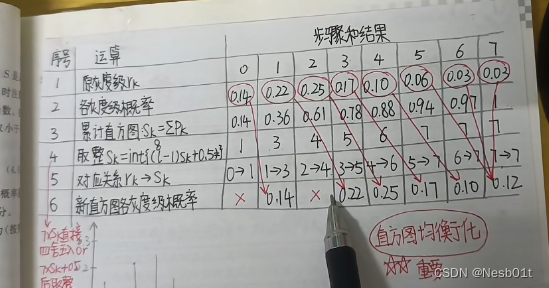
6. 画出均衡化后的直方图
根据上面的数据重新画直方图,需要注意的是:
- 下面的 X 轴变成了 0、1/7、2/7 … 1
- 如果上面数据有的是空的,就是 0










![VCP-DCV VMware vSphere:安装、配置和管理[V8.x]](https://img-blog.csdnimg.cn/d411ff8169bc4e6883a328b07f076f47.png)