背景

诺贝尔奖 在他逝世的前一年，立嘱将其遗产的大部分(约920万美元)作为基金，将每年所得利息分为5份，设立物理、化学、生理或医学、文学及和平5种奖金(即诺贝尔奖)，授予世界各国在这些领域对人类作出重大贡献的人。其中炸药为最为出名的一项。人造元素锘(Nobelium)就是以诺贝尔命名的。（1968年又增设经济学奖），每年在诺贝尔逝世日12月10日颁发，以表彰在以上各个领域对人类作出难以磨灭的伟大贡献的人们。

 【模型假设】

1. 每年奖金金额一定，一次性在年底支出
2. 基金经营期间，基金的年收益率不变
3. 当年年初的基金额等于上年基金额的本息减去奖金额
4. 基金的累计按照复利计算

【符号说明】

 【建立模型】

根据假设（1）-（4），第t年年末有基金额为At，第t+1年基金收益为At(1+r)，再支出奖金金额B，就是第t+1年年末基金额At+1，即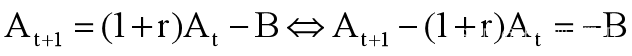【22】

这是一个一阶常系数非齐次差分方程，其对应的齐次方程的通解为【23】

易观察【22】的一个特解为所以【22】的通解为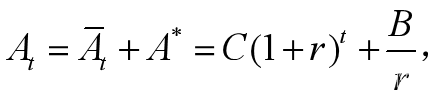

又由初值条件A0，得到【22】的特解为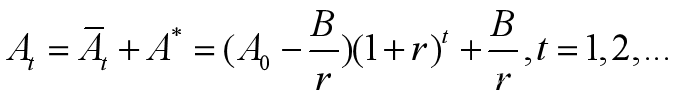【24】

其中，A0,B,r,At中只要知道三个，就可以求出剩下一个。 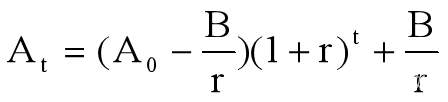【24】

【模型应用】 

某企业以该企业命名建立一项奖励基金，计划每年年终发放一次，奖金为一万元，如果基金的年收益率为15%，奖金发放年限为10年，则以复利计算，原始基金应为多少？如果是永续基金，原始基金又为多少？

1、发放年限10年，初始基金如何？

发放年限为十年，意味着第10年末基金余额为0，即A10=0, r=0.15，B=10000，代入【24】，得 

 

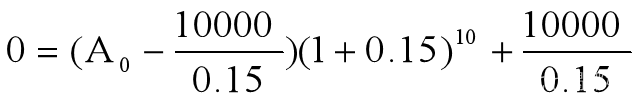
解之得：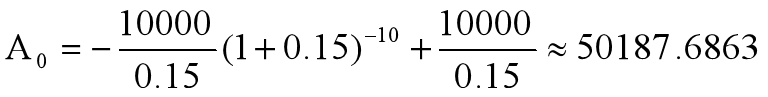 

2、若做成永续系基金，又如何？ 

  如果是永续基金，意味着每一年年末发放奖金后，基金余额不低于年初基金的数值，即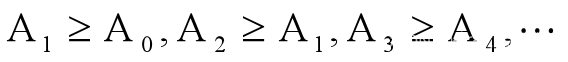 

不妨取A1>=A0，即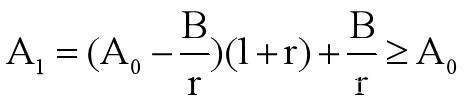

 等价变形得（即所发奖金不能超过年利息）

将B=10000，r=0.15代入上式， 得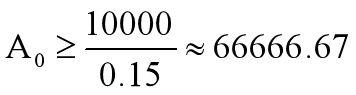

 为了管理层普通人员便于管理，现将10年期限基金和永续基金的逐年运作数据列于表1和表2。

                                  表1 10年基金运作一览表：r=0.15  单位（元） 

年份	年初基金	年底末基金	发放奖金	基金余额
1	50187.68	57715.84	10000	47715.84
2	47715.84	54873.22	10000	44873.22
3	44873.22	51704.20	10000	41704.20
4	41604.20	47844.83	10000	37844.83
5	37844.83	43521.55	10000	33521.55
6	33521.55	38549.78	10000	28549.78
7	28549.78	32832.25	10000	22832.25
8	22832.25	26257.09	10000	16257.09
9	16257.09	18695.65	10000	8695.65
10	8695.65	10000.00	10000	0.00

                                     表2   永续基金运作一览表：r=0.15  单位（元）

年份	年初基金	年底末基金	发放奖金	基金余额
1	66666.67	76666.67	10000	66666.67
2	66666.67	76666.67	10000	66666.67
3	66666.67	76666.67	10000	66666.67
…	…	…	…	…
10	66666.67	76666.67	10000	66666.67
…	…	…	…	…

 3、模型推广

基金的创始者如果考虑到通货膨胀，考虑每年发放的奖金不是固定的，而是每年递增5%，该如何运作这项基金？

设初始奖金金额为B，并且每年递增的比例为5%。假设每年的通货膨胀率为r。

1. 第一年后，奖金金额为B。
2. 第二年后，奖金金额为B + B * 0.05 - B * r。
3. 第三年后，奖金金额为B + (B + B * 0.05 - B * r) * 0.05 - (B + B * 0.05 - B * r) * r。
4. 以此类推，第n年后的奖金金额为前一年奖金金额加上前一年奖金金额乘以0.05，再减去前一年奖金金额乘以通货膨胀率r。

这个差分方程可以写成递推式的形式：

B(n) = B(n-1) + B(n-1) * 0.05 - B(n-1) * r

其中，B(n)表示第n年后的奖金金额，B(n-1)表示第n-1年后的奖金金额。

使用这个递推式，你可以计算每年的奖金金额并进行预测。需要注意，通货膨胀率r可能会每年变化，所以在实际运作中，你需要根据实际情况进行调整。

4、模型对比

将基金管理模型与还房贷模型对比，有何异同？

相似之处：

1. 都是基于数学模型来进行管理和规划的。
2. 都涉及到资金的增长或减少，通过规划和决策来实现长期目标。
3. 都需要考虑时间价值的因素，如利息、回报率等。

差异之处：

1. 对象不同：基金管理模型是应用于投资基金等金融工具的管理，而房贷模型是应用于购房者贷款还款的模型。
2. 目标不同：基金管理模型的目标通常是实现资金的增值，从而使投资者获得回报；房贷模型的目标是管理借款人的还款计划，确保按时偿还贷款。
3. 风险和收益：基金管理涉及更多的投资风险和回报预期，需要管理人员进行投资决策和风险控制；房贷模型更多地关注还款能力和管理风险，以确保按时还款而不会陷入经济困境。
4. 时间尺度：基金管理模型通常用于长期投资，涉及更长的时间尺度，可能需要考虑更多的市场波动和周期性因素；房贷模型通常涉及中长期还款计划，通常以月或年为单位。

尽管基金管理模型和房贷模型有相似之处，但由于它们的不同目标和应用领域，其模型和方法有所不同。对于每种模型，都需要根据具体情况进行定制和调整，以满足特定的管理需求。