任务描述
Python 中存在着一个特殊的函数:生成器。生成器是一个“函数对象”,它与函数的定义在形式上完全相同,具有“函数名”与“参数列表”,不同之处在于它可以以yield方式“暂时返回”。
本关的任务是让学习者掌握 Python 中生成器的使用方法,然后利用生成器实现一个计算 π 的具有 O(N) 复杂度的算法。
相关知识
生成器的特点
当从别处调用的生成器暂时返回后,生成器会记住上次的返回点;当对该生成器再次调用(使用next()方法)时,它会从生成器上次的返回点继续执行,而不是从头开始执行该被调函数;此外,上次调用返回时的“上下文”在下次调用时也会恢复。
恰当的使用生成器,可以有效地降低使用标准函数时的计算复杂度。下面以斐波那契函数为例介绍如何使用生成器来实现。
基于生成器的斐波那契函数实现
斐波那契数列中的第 n 项 F(n) 可由下面的递推公式计算获得:
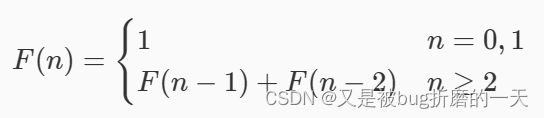
如果要计算 ∑i=0nF(i) 的值,大致有下面两种方法。
第一种方法,按表达式通过定义函数计算:定义一个函数计算 F(i) ,而后用一个循环将这些计算结果累加。因为计算 F(i) 需要 O(i) 次加法,这使得整个运算的复杂度为 O(n2) 。
第二种方法,使用全局变量:将当前的 i、F(i)、F(i+1) 分别保存在全局变量 i、a、b 中,可以获得时间开销为 O(n) 的算法。然而,这种方法不具有扩展性 —— 当需要存储的全局变量非常多的时候,会破坏程序的数据封装性。
我们可以使用一个生成器,在避免使用过多全局变量的情况下获得开销为 O(n) 的算法,代码如下。
def fib():
a = 1
b = 1
yield a # 第一次的返回值
yield b # 第二次的返回值
while True:
a,b = b, a+b
yield b # 后面项的返回值
s = 0
f = fib
n = input()
for i in range(n+1):
s += next(f)
print s利用一个跟踪调试器,理解上述代码的执行,并弄明白为什么只需要 O(n) 次计算。
基于韦达公式的圆周率计算方法
在微积分诞生之前,法国数学家韦达于 1593 年发表了关于 π 的一个计算公式,也就是 Vieta(韦达)公式 :

那么就有 2π≈∏i=0Nai 。
使用该公式,我们可以计算出 π 的值。
编程要求
本关的编程任务是利用生成器,基于韦达公式给出计算 π 的具有 O(N) 复杂度的算法。
具体实现的代码框架如下:
# coding:utf-8
from math import sqrt
def Vieta():
#请在此输入代码
#********** Begin *********#
a = sqrt(2)/2.0
while True:
yield a
a = sqrt((1.0+a)/2.0)
#********** End *********#
N = int(input())
v = Vieta(); p = 1.0
for i in range(N+1):
# 请在此输入代码
# ********** Begin *********#
p = p*next(v)
# ********** End *********#
print ("%.6f"%(2.0/p))
本实训测试样例如下:
测试输入: 20
预期输出: 3.141593
提问:上述代码中为什么要用while true呢,意义在哪里,如果不加while true能行吗
在上述代码中,使用
while True创建了一个无限循环,这是为了生成器函数leibniz_generator()能够无限产生项的值。这是因为韦达公式中的级数是无限的,所以我们需要一个无限循环来不断生成这些项。如果不使用
while True,而是使用某个固定的循环次数,那么就无法得到π的精确值,因为你无法确定需要多少项才能达到所需的精度。通过使用while True,我们可以根据需要生成尽可能多的项,直到满足精度要求为止。一旦某一项的值小于所需的精度,我们就可以在calculate_pi()函数中使用break语句来退出循环,从而计算出近似值。因此,
while True在这里的意义是创建一个无限循环,使得生成器能够按需生成无限多的项,以便在满足精度条件时停止。如果不使用无限循环,代码将会限制了项数,无法获得所需的精确度。