位图原理及实现
- 位图概念
- 位图实现
- 构造函数
- set成员函数
- reset成员函数
- test成员函数
- 位图的应用
位图概念
给40亿个不重复的无符号整数,没排过序。给一个无符号整数,如何快速判断一个数是否在这40亿个数中。
对于上面这道题大多数人都会想到用遍历和二分查找的方法去解决,但是会存在一个问题,40亿个unsigned int类型的整数,所占内存空间大约在16G左右了,这样大的空间内存当中是放不下的,那么应该怎么办呢?
我们可以用位图来解决这个问题:
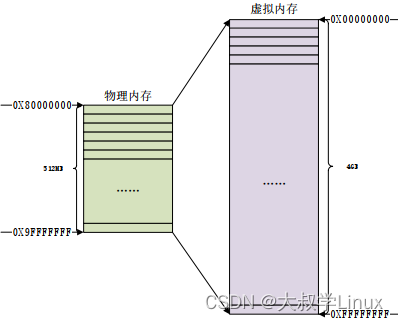
我们会发现无符号整数有2^ 32 个,而我们如果以bit位来计量的话,就只需要 2^32个bit位,也就是512MB的空间,内存当中是可以进行存储的,那么我们该如何进行操作呢?
我们需要判断的是一个数在不在,我们就假设存在bit位就是1,不存在bit位就是0,我们以char类型来进行划分,一个char类型数据就占8个bit位,如下图所示:

位图实现
构造函数
一个char类型型有8个比特位,因此N个位的位图就需要用到N/8个,但是实际我们所需的整型个数是N/8+1,因为所给非类型模板参数N的值可能并不是8的整数倍。
例如:N=27,N/8+1 = 3+1 = 4;

template<size_t N>
class bitset
{
public:
//构造函数
bitset()
{
_bits.resize(N / 8 + 1, 0);
}
private:
vector<char> _bits;
};
set成员函数
set成员函数用于设置位,设置位的方法如下:
- 计算 x 位所在的第 i 个位置所占的第 j 个bit位;
- 将1左移 j 位后与第 i 个位置进行 | 运算即可;

void set(size_t x)
{
size_t i = x / 8;
size_t j = x % 8;
//计算x位所在的第i个位置所占的第j个bit位
_bits[i] |= (1 << j);
//将该设置为1
}
reset成员函数
reset成员函数用于清空位,清空位方法如下:
- 计算 x 位所在的第 i 个位置所占的第 j 个bit位;
- 将1左移 j 位再按位取反后与第 i 个位置进行 & 运算即可。

void reset(size_t x)
{
size_t i = x / 8;
size_t j = x % 8;
//计算x位所在的第i个位置所占的第j个bit位
_bits[i] &= ~(1 << j);
//将该设置为0
}
test成员函数
test成员函数用于获取位的状态,方法如下:
- 计算x位所在的第 i 个位置所占的第 j 个bit位;
- 将1左移 j 位后与第 i 个位置进行 & 运算得出结果。
- 若结果非0,则该位被设置,否则该位未被设置。
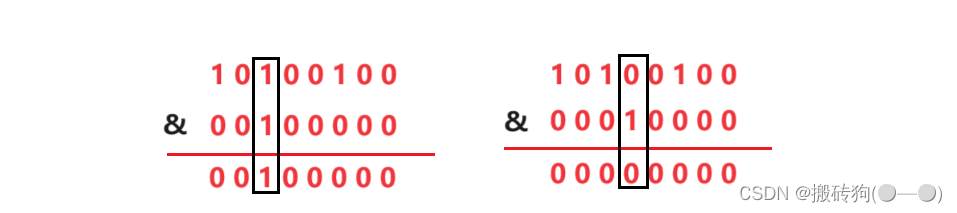
bool test(size_t x)
{
size_t i = x / 8;
size_t j = x % 8;
//计算x位所在的第i个位置所占的第j个bit位
return _bits[i] = (1 << j);
}
位图的应用
- 快速查找某个数据是否在一个集合中;
- 排序 + 去重;
- 求两个集合的交集、并集等;
- 操作系统中磁盘块标记。
我们来看几道题目:
- 给定100亿个整数,设计算法找到只出现一次的整数?
我们可以将整数标记为3种状态:
- 出现0次;
- 出现1次;
- 出现2次或者2次以上。
一个位只能表示两种状态,而要表示三种状态我们至少需要用两个位,因此我们可以开辟两个位图,这两个位图的对应位置分别表示该位置整数的第一个位和第二个位。
我们可以将着三种状态分别定义为00、01、10,此时当我们读取到重复的整数时,就可以让其对应的两个位按照00→01→10的顺序进行变化,最后状态是01的整数就是只出现一次的整数。
template<size_t N>
class twobitset
{
public:
void set(size_t x)
{
bool insert1 = bt1.test(x);
bool insert2 = bt2.test(x);
//00
if (insert1 == false && insert2 == false)
{
//->01
bt2.set(x);
}
else if (insert1 == false && insert2 == true)
{
//->10
bt1.set(x);
bt2.reset(x);
}
}
void print_once_num()
{
for (size_t i = 0; i < N; i++)
{
if (bt1.test(i) == false && bt2.test(i) == true)
{
cout << i << endl;
}
}
}
private:
bitset<N> bt1;
bitset<N> bt2;
};
- 给两个文件,分别有100亿个整数,我们只有1G内存,如何找到两个文件的交集?
方案一:(一个位图需要512M内存)
- 依次读取第一个文件中的所有整数,将其映射到一个位图。
- 再读取另一个文件中的所有整数,判断在不在位图中,在就是交集,不在就不是交集。
方案二:(两个位图刚好需要1G内存,满足要求)
- 依次读取第一个文件中的所有整数,将其映射到位图1。
- 依次读取另一个文件中的所有整数,将其映射到位图2。
- 将位图1和位图2进行与操作,结果存储在位图1中,此时位图1当中映射的整数就是两个文件的交集。
- 一个文件有100亿个整数,1G内存,设计算法找到出现次数不超过2次的所有整数。
该题跟题目一的做法一样,我们将数据标记为4种状态:
- 出现0次。
- 出现1次。
- 出现2次。
- 出现2次以上。
template<size_t N>
class twobitset
{
public:
void set(size_t x)
{
bool insert1 = bt1.test(x);
bool insert2 = bt2.test(x);
//00
if (insert1 == false && insert2 == false)
{
//->01
bt2.set(x);
}
else if (insert1 == false && insert2 == true)
{
//->10
bt1.set(x);
bt2.reset(x);
}
else if (insert1 == true && insert2 == true)
{
//->11
bt1.set(x);
bt2.set(x);
}
}
void print_twice_num()
{
for (size_t i = 0; i < N; i++)
{
if ((bt1.test(i) == false && bt2.test(i) == true) || (bt1.test(i) ==true && bt2.test(i) == true))
{
cout << i << endl;
}
}
}
private:
bitset<N> bt1;
bitset<N> bt2;
};