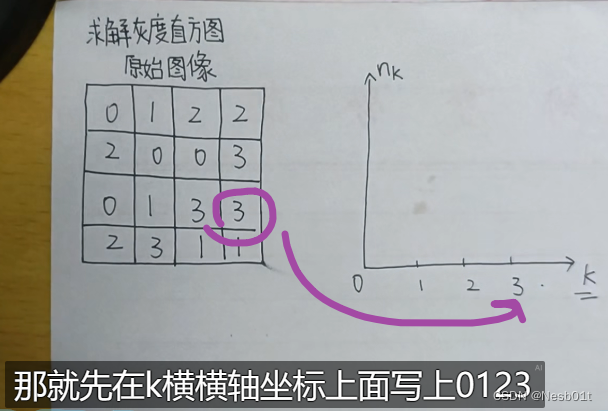
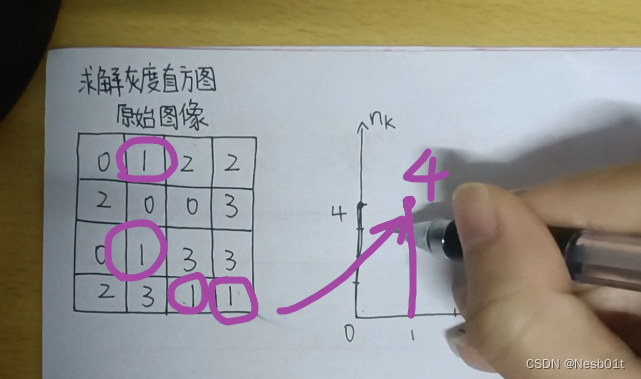
求解灰度直方图，如何绘制灰度直方图（数字图像处理大题复习 P1）
news2025/1/11 20:50:16
本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1017174.html
如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！相关文章
element -ui table表格内容无限滚动 使用插件vue-seamless-scroll
使用插件
一、安装组件依赖 npm install vue-seamless-scroll
二、引入组件
import vueSeamlessScroll from "vue-seamless-scroll";
components: { vueSeamlessScroll }, <div class"table-list "><vue-seamless-scroll :class-option"…
JavaWeb概念视频笔记
学习地址：102.尚硅谷_Tomcat-Tomcat服务器和Servlet版本的对应关系_哔哩哔哩_bilibili 目录
1.JavaWeb的概念
2.Web资源的分类
3.常用的Web服务器
4.Tomcat服务器和Servlet版本的对应关系
5.Tomcat的使用
a.安装
b.目录介绍
c.如何启动 Tomcat 服务器
另一…
【C语言】指针和数组笔试题解析（1）
指针是C语言的灵魂，他的玩法多种多样，这篇文章带来指针的笔试题详解，可以帮助我们更好的理解与巩固指针的知识 目录 预备知识：题目：一维数组：二维数组： 题目比较多，但切记戒骄戒躁&a…
Selenium常用操作之单选复选框、下拉列表、键盘、截屏、断言、(显式隐式)等待
目录
1. 窗口最大化
2.单选框操作
3. 复选框操作
4. 下拉列表
5. selenium 三种等待
6. 键盘操作
7.截屏
8.断言
9. Selenium操作JS弹窗控件
10.鼠标悬停与释放 1. 窗口最大化
driver.maximize_window()
2.单选框操作 driver.find_element_by_xpath("//input[…
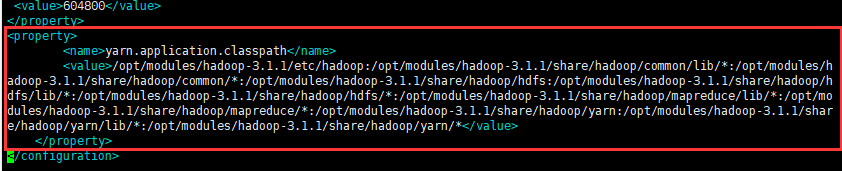
Hdoop伪分布式集群搭建
文章目录 Hadoop安装部署前言1.环境2.步骤3.效果图 具体步骤（一）前期准备（1）ping外网（2）配置主机名（3）配置时钟同步（4）关闭防火墙 （二）…
Linux学习第13天：嵌入式LinuxLED驱动开发：一字一符总见情
在正式写这篇笔记前，有一个事情必须要说一下。昨天更新的基于API函数的字符设备驱动开发按照正常的教程来说应该在本笔记后一天更新才对。但是由于我一时的疏忽，跳过了本笔记。在昨天学习基于API函数的时候造成了一定程度的困扰。今天重翻教程的时候才发…
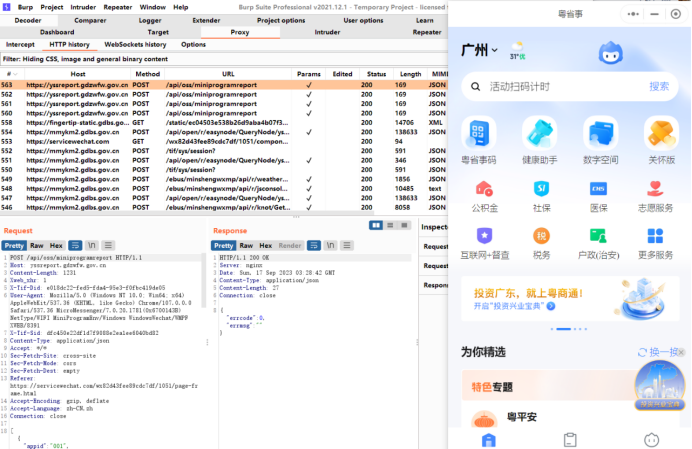
burp+IE 微信小程序抓包教程
文章目录 一、BURP里新增监听端口二、BURP导出证书三、导入证书四、IE代理设置五、小程序抓包实际测试 一、BURP里新增监听端口
找一个没用的端口，使用以下方式新增
二、BURP导出证书
选择刚才新增的监听端口，点击证书导入导出
将其存出来即可&…
Maven知识点总结
Maven 基础课程第一天 第1章 Maven 介绍
1.1什么是 Maven
1.1.1什么是 Maven
Maven 的正确发音是[ˈmevən]，而不是“马瘟”以及其他什么瘟。Maven 在美国是一个口语化的词语，代表专家、内行的意思。 一个对Maven 比较正式的定义是这么说的࿱…
notepad++ 配置 python 以及Anaconda中的python（已解决）
说明，无论是自己的电脑单独安装的python 还是Anaconda虚拟环境安装的python都是一样的。区别就是 独立安装的python 的exe文件路径添加的环境变量了，不需要制定它的路径直接运行下面的命令就可以，而Anaconda中的python.exe的文件夹并没有在虚…
endnotes插入文献突然变得格式不对，而且也不是按照正常的顺序来插入解决办法
今天插入文献突然变成了endnotes里面的文献序号，而且也不导入了，多了作者和序号信息
解决办法： 更新一下，然后在进行的导入就ok了，能够按照以前的格式插入了，序号也能自动排开，而且也能导入文献…
从CNN（卷积神经网络），又名CAM获取热图
一、说明 卷积神经网络（CNN）令人难以置信。如果你想知道它如何看待世界（图像），有一种方法是可视化它。 这个想法是，我们从最后的密集层中得到权重，然后乘以最终的CNN层。这需要全局平均…
想要精通算法和SQL的成长之路 - 戳气球
想要精通算法和SQL的成长之路 - 戳气球 前言一. 戳气球1.1 记忆化搜索 前言 想要精通算法和SQL的成长之路 - 系列导航 一. 戳气球
原题链接
首先我们看一下题干：对于超出了数组边界的，就当做它是一个数字为1的气球。遇到这种的，我们可以考…
论文解读-DeepEdit：使用纳米孔直接RNA测序对A - to - I RNA编辑事件进行单分子检测和阶段划分
DOI： 10.1186/s13059-023-02921-0
期刊 ：Genome Biology
中科院分区：1Q
影像因子：12.3
作者 Longxian Chen; Liang Ou; Xinyun Jing; Yawei Kong; Bingran Xie; et al
出版日期 2023-04-17
网址： https://genome…
Jetpack系列 -- LiveData源码原理解析（解决黏性问题）
一、LiveData是什么？
注意：一般情况下，LiveData要配合ViewModel一起使用的，但是今天是单独使用LiveData，作为学习的话，我们可以只关注LiveData了。
LiveData是一种可观察的数据存储器类。与常规的可观察类…
python-保留小数位数的3种方法
在python实际运用中，需要对小数位数进行截取保留。 以下是，python保留小数点位数的3种方法。
方法一
方法：’%.nf’ % num n代表保留的小数位数，num表示需要截取的目标数 用法如下：
old_num 1.23456
new_num %.2f…
![[NLP] LLM---＜训练中文LLama2(四)方式一＞对LLama2进行SFT微调](https://img-blog.csdnimg.cn/bec50e7544ad455fba2cd4cfac385af9.png)
[NLP] LLM---＜训练中文LLama2(四)方式一＞对LLama2进行SFT微调
指令精调
指令精调阶段的任务形式基本与Stanford Alpaca相同。训练方案也采用了LoRA进行高效精调，并进一步增加了可训练参数数量。在prompt设计上，精调以及预测时采用的都是原版Stanford Alpaca不带input的模版。对于包含input字段的数据，采…
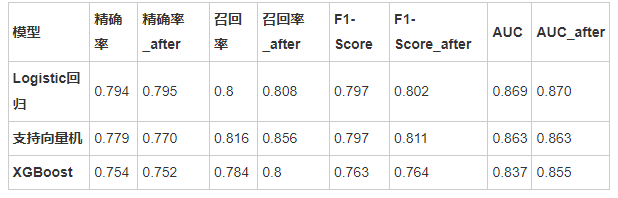
竞赛 基于机器学习与大数据的糖尿病预测
文章目录 1 前言1 课题背景2 数据导入处理3 数据可视化分析4 特征选择4.1 通过相关性进行筛选4.2 多重共线性4.3 RFE（递归特征消除法）4.4 正则化 5 机器学习模型建立与评价5.1 评价方式的选择5.2 模型的建立与评价5.3 模型参数调优5.4 将调参过后的模型重…
yolov5在rk3588上加速
不采用fastdeploy等三方框架，使用rknn-lite2或者rknpu在rk3588上加速，测试加速的是rknn自带的yolov5模型。
备注：
1.测试视频：多人，帧:3000，时长:2min，分辨率:1920x1080，fps:25
2…
傅里叶变换应用 （02/2）：频域和相位
一、说明 到目前为止，在我们的讨论中，我已经交替使用了“傅里叶变换”和“快速傅里叶变换（FFT）”。在这一点上，值得注意的是区别！FFT 是“离散”傅里叶变换 （DFT） 的有效算法实现。“…
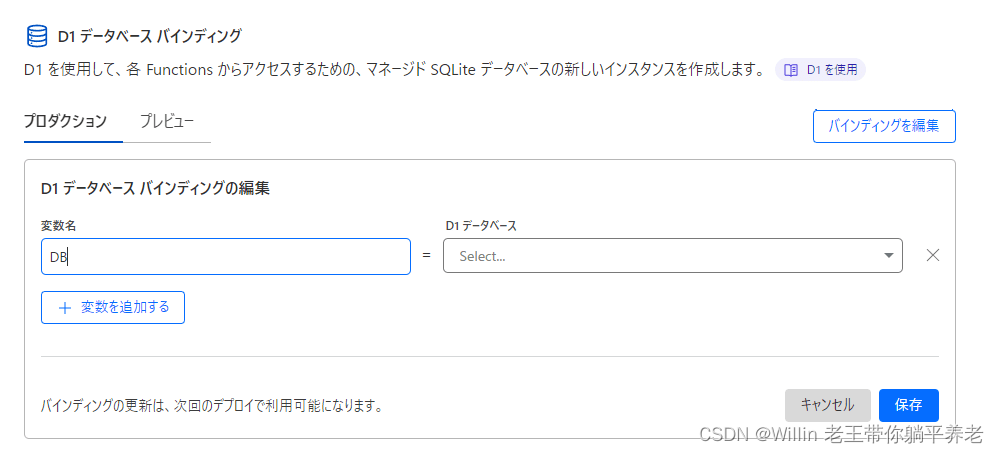
Remix+Cloudflare Pages+D1 快速上手
我们最近听到越来越多的关于Cloudflare的服务。
我对Clouflare D1特别感兴趣，所以我决定研究一下。
与这次我想使用的 Remix 一起，我想介绍 Remix Cloudflare Pages D1 的第一步。
我只是稍微地了解一下，但我所做的在下面的仓库中&#…