能够可视化的查看对于理解图神经网络(gnn)越来越重要，所以在这篇文章中，我将介绍传统GNN层的实现，然后展示ICLR论文“图注意力网络”中对传统GNN层的改进。

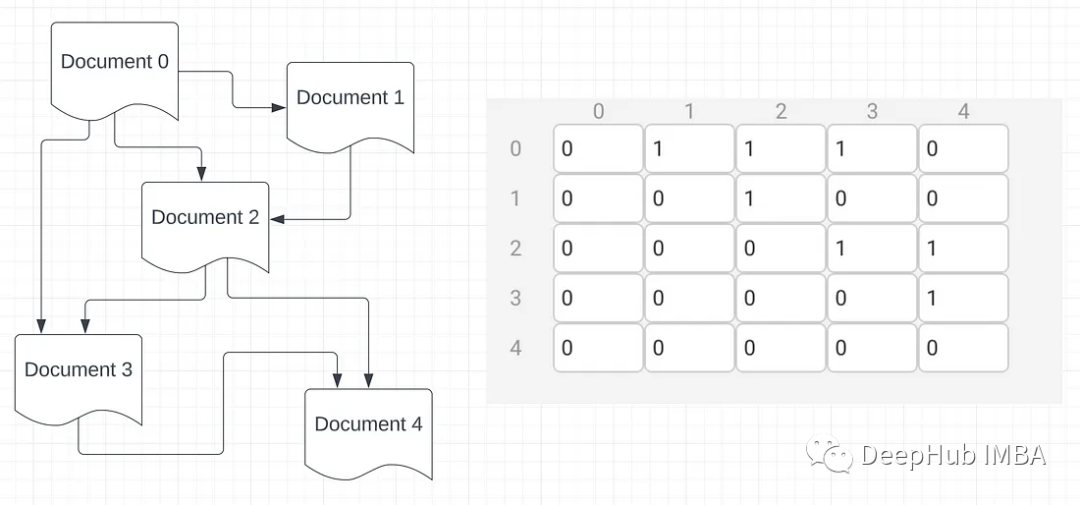
假设我们有一个表示为有向无环图(DAG)的文本文档图。文档0与文档1、2和3有一条边，为了实现可视化，这里将使用Graphbook，一个可视化的人工智能建模工具。

我们还为每个文档提供了一些节点特征。将每个文档作为单个[5] 1D文本数组放入BERT中，这样就得到了一个[5,768]形状的嵌入。

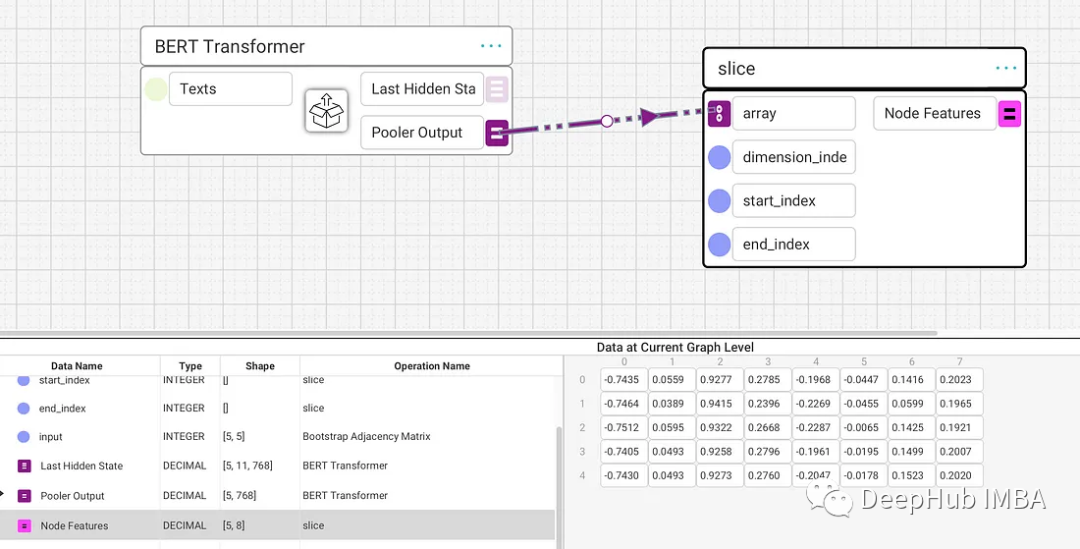
为了方便演示，我们只采用BERT输出的前8个维度作为节点特征，这样可以更容易地跟踪数据形状。这样我们就有了邻接矩阵和节点特征。

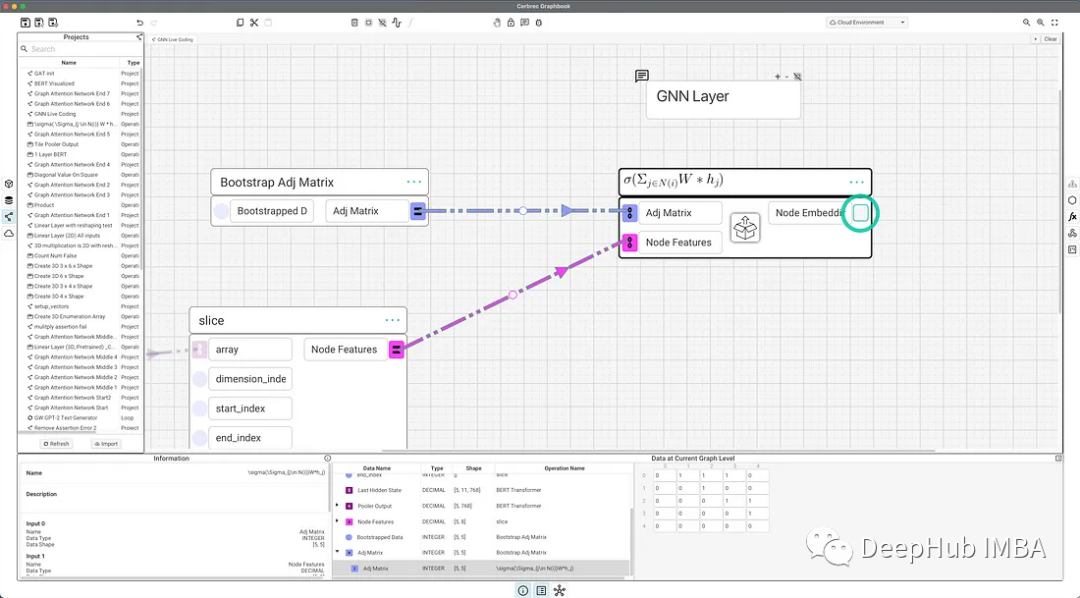
GNN层

GNN层的一般公式是，对于每个节点，我们取每个节点的所有邻居对特征求和，乘以一个权重矩阵，最后通过一个激活函数得到输出结果。所以这里创建一个以这个公式为标题的空白块，并将其传递给Adj矩阵和节点特征，我将在块中实现上面说的公式。

我们将节点特征平铺(即广播)为3D形状，也就初始的[5,8]形状的节点特征，扩展成有[5,5,8]形状，其中第0维的每个单元格都是节点特征的重复。所以现在可以把最后一个维度看作是“邻居”特征。每个节点有5个可能的邻居。

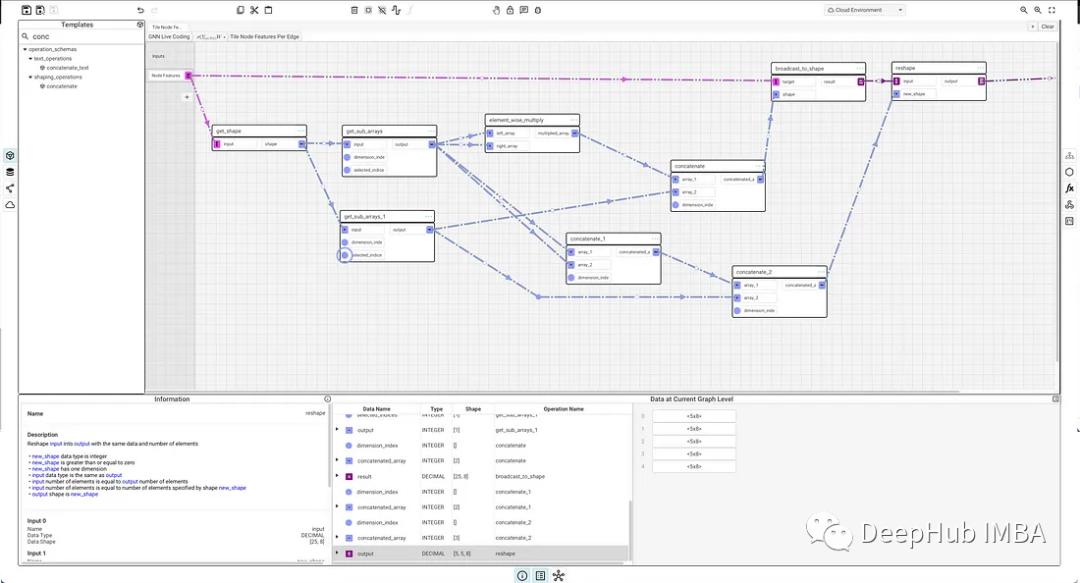
因为不能直接将节点特征从[5,8]广播到[5,5,8]，我们必须首先广播到[25,8]，因为在广播时，形状中的每个维度都必须大于或等于原始维度。所以得到形状的5和8部分(get_sub_arrays)，然后乘以第一部分得到25，然后将它们全部连接在一起。将结果[25,8]重塑回[5,5,8]，结果可以在Graphbook中验证最终2维中的每个节点特征集是相同的。

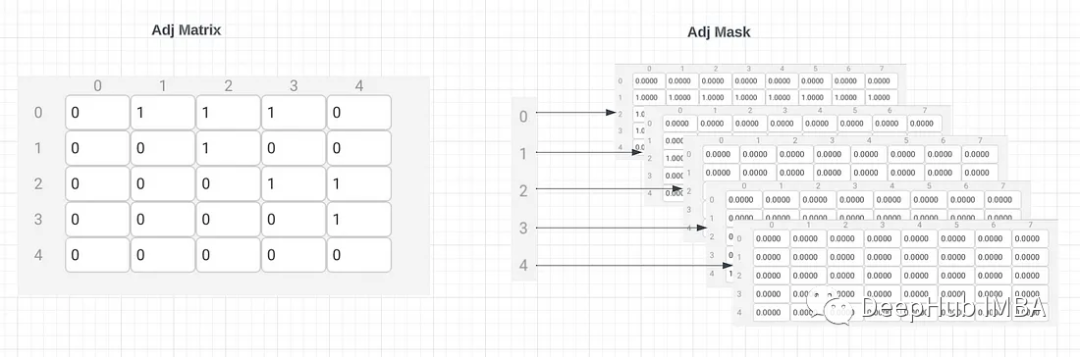
下一步就是广播邻接矩阵到相同的形状。对于第i行和col j的邻接矩阵中的每一个1，在维数[i, j]上有一行1.0的num_feat。所以在这个邻接关系中，在第0个单元格中第1、2和3行有一行num_feat 1.0(即[0,1:3，:])。

这里的实现非常简单，只需将邻接矩阵解析为十进制并从[5,5]形状广播到[5,5,8]。将这个邻接掩码与平铺节点邻居特征相乘。

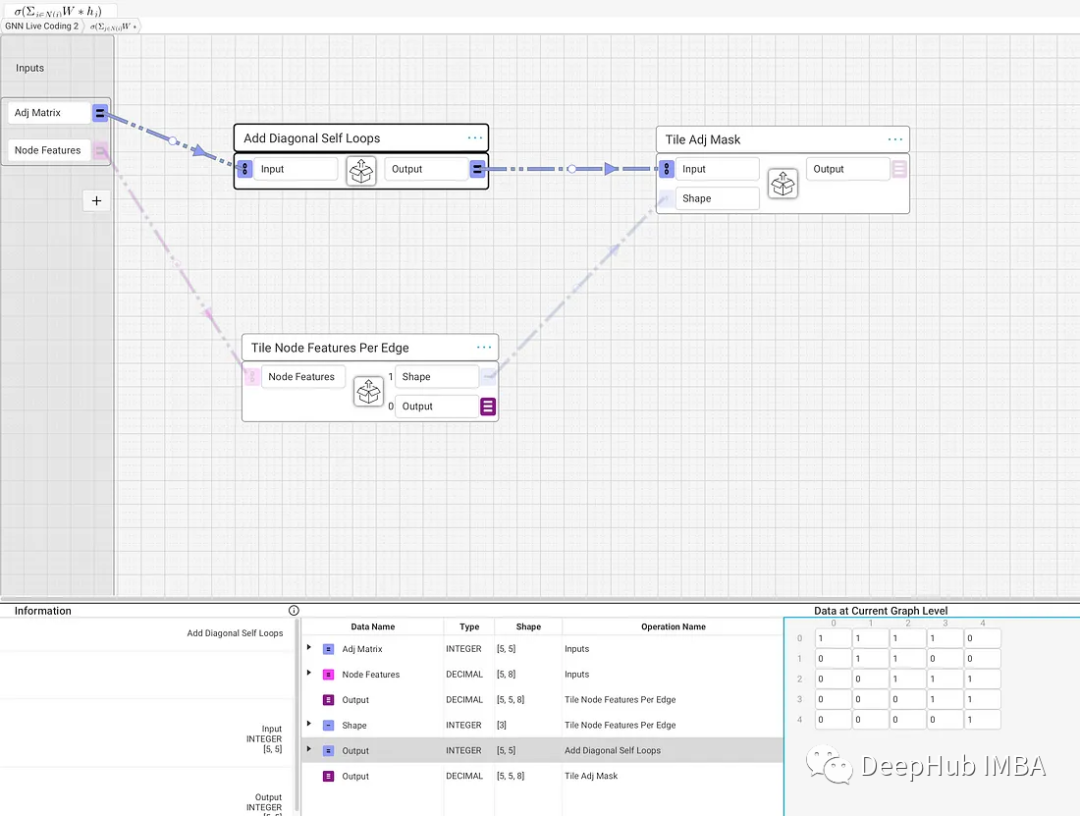
我们还想在邻接矩阵中包含一个自循环，这样当对邻居特征求和时，也包括了该节点自己的节点特征。

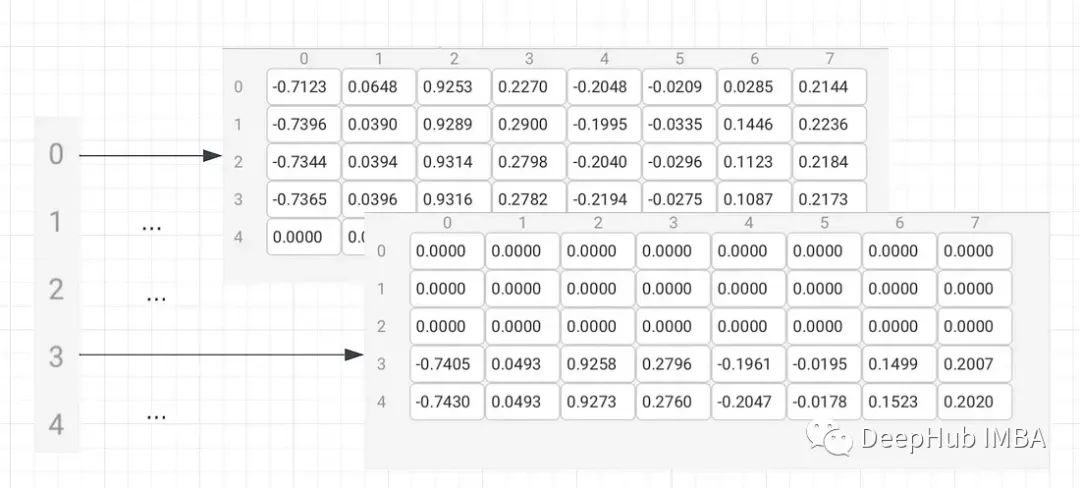
这样就得到了每个节点的邻居特征，其中没有被一条边连接的节点(不是邻居)的特征为零。对于第0个节点，它包括节点0到3的特征。对于第三个节点，它包括第三和第四个节点。

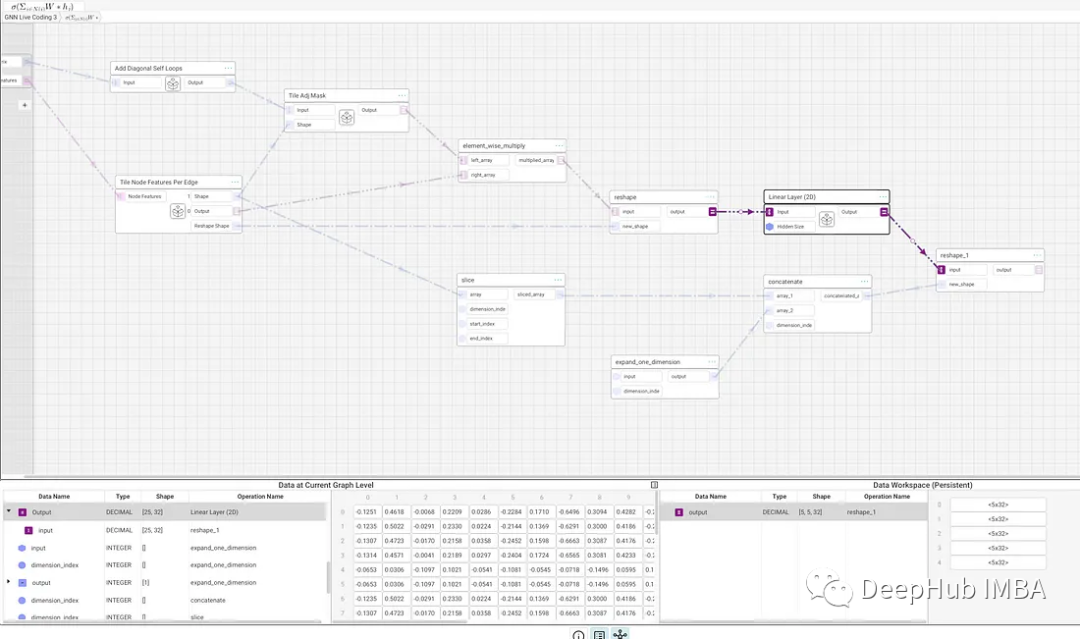
下一步就是重塑为[25,8]，使每个相邻特征都是它自己的行，并将其传递给具有所需隐藏大小的参数化线性层。这里隐藏层大小是32并保存为全局常量，以便可以重用。线性层的输出将是[25,hidden_size]。所以经过重塑就可以得到[5,5,hidden_size]。

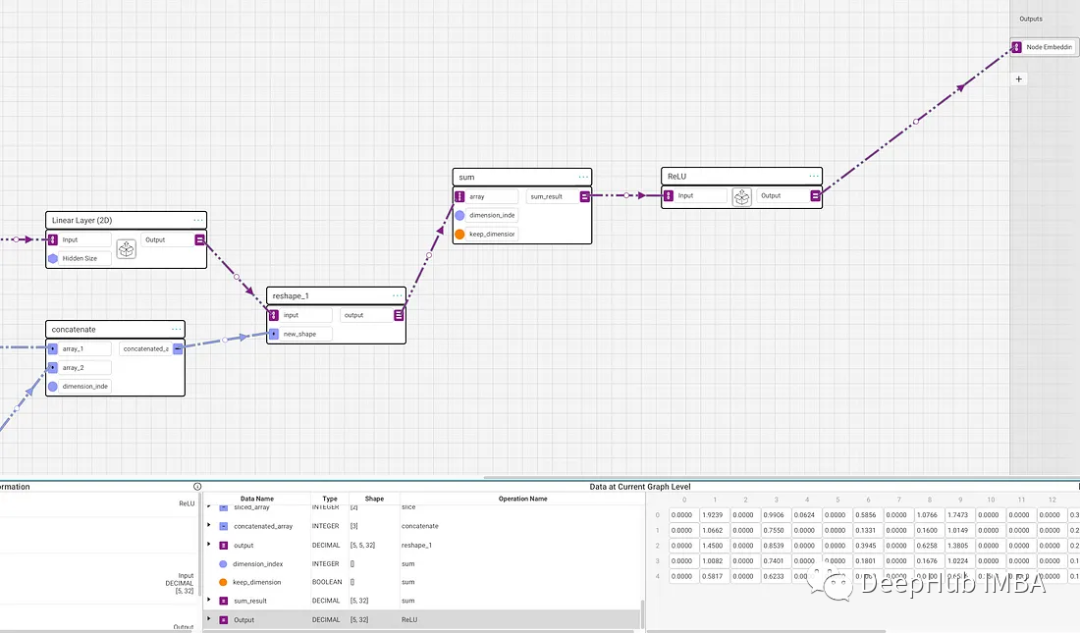
最后对中间维度(维度索引为1)求和，对每个节点的相邻特征求和。结果是经过1层的节点嵌入集[5,hidden_size]，得到了一个GNN网络。

图注意力层

图注意层关键是注意力系数，如上式所示。从本质上讲，在应用softmax之前，我们将边缘中的节点嵌入连接起来，并通过另一个线性层。

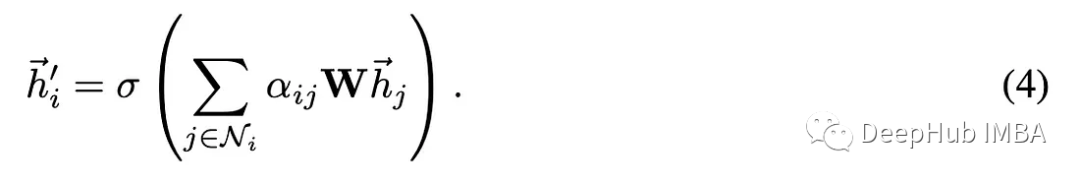
然后使用这些注意系数来计算与原始节点特征对应的特征的线性组合。

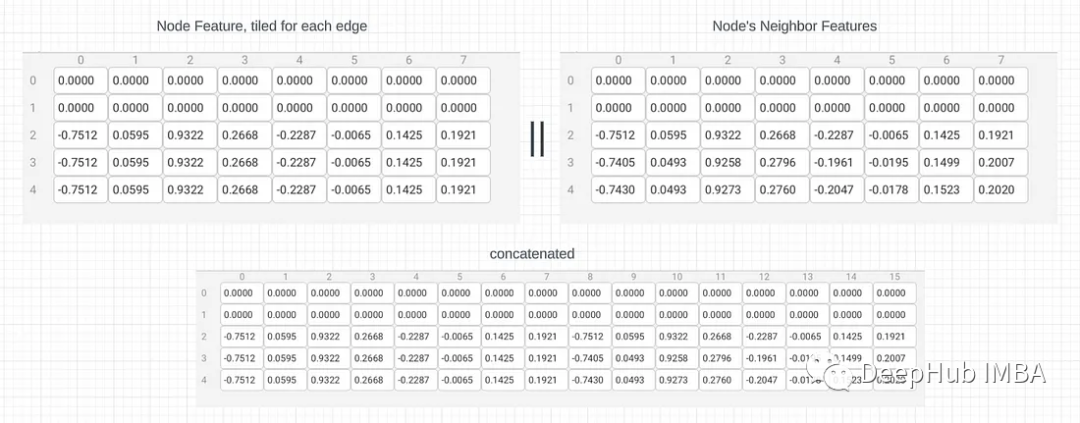
我们要做的是为每个邻居平铺每个节点的特征，然后将其与节点的邻居特征连接起来。

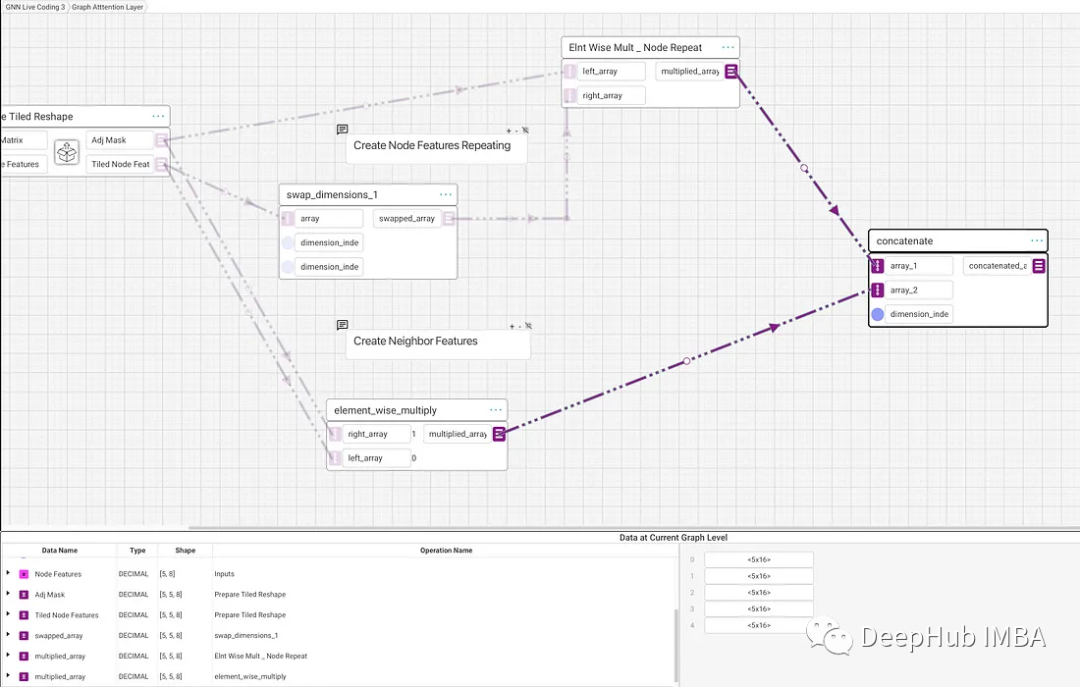
这里需要注意的是mask掩码需要在平铺节点特征之前交换0和1维。

这用结果仍然是一个[5,5,8]形数组，但现在[i，:，:]中的每一行都是相同的，并且对应于节点i的特征。然后我们就可以使用乘法来创建只在包含邻居时才重复的节点特征。最后就是将其与上面的GNN创建的相邻特征连接起来，生成连接的特征。

现在我们有了连接的特征，需要把它们输入到一个线性层中，所以还需要重塑回到[5,5,hidden_size]，这样我们就可以在中间维度上进行softmax产生我们的注意力系数。

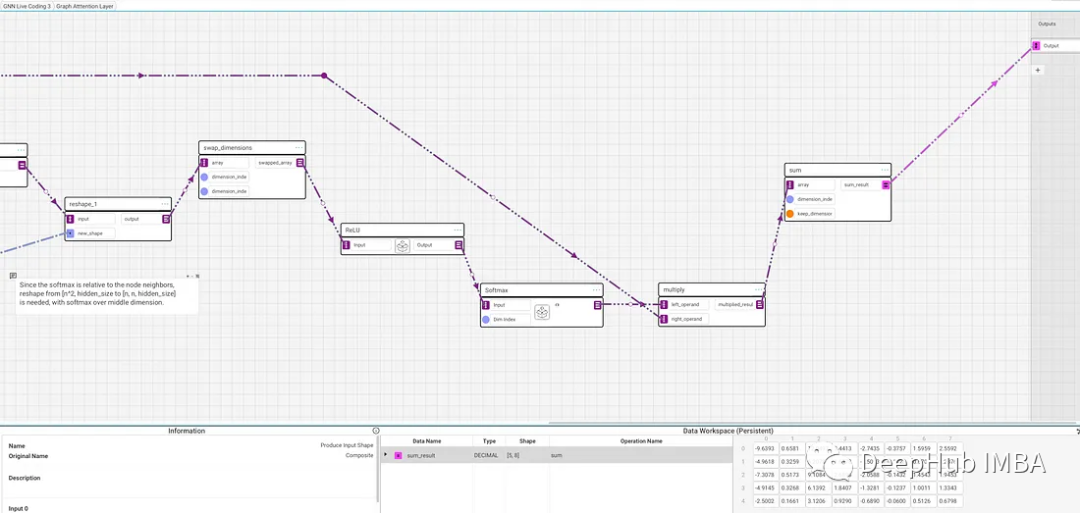
得到了形状为[5,5,hidden_size]的注意力系数，这实际上是在n个节点的图中每个图边嵌入一次。论文说这些应该被转置(维度交换)，我们在ReLU之前已经做过了，现在我对最后一个维度进行softmax，这样它们就可以沿着隐藏的尺寸维度进行每个维度索引的标准化。

将[5,hidden_size, 5]形状乘以[5,5,8]形状得到[5,hidden_size, 8]形状。然后我们对hidden_size维度求和，最终输出[5,8]，匹配我们的输入形状。这样就可以把这个层串起来多次使用。

总结

本文介绍二零单个GNN层和GAT层的可视化实现。在论文中，他们还解释了是如何扩展多头注意方法的，我们这里没有进行演示。

Graphbook是用于AI和深度学习模型开发的可视化IDE，Graphbook仍处于测试阶段，但是他却是一个很有意思的工具，通过可视化的实现，我们可以了解更多的细节。

https://avoid.overfit.cn/post/3cb8ab327fe3416d8b459ad9bc004b0d

作者：David Winer