基于WIN10的64位系统演示

一、写在前面

从这一期开始，我们开始基于python构建各种机器学习和深度学习的时间序列预测模型，本质上就是调用各种模型的回归分析的属性。所以很多模型其实之前都介绍过，比如说决策树、SVM等等。

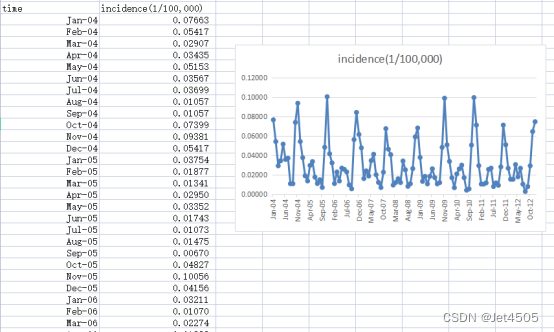
同样，这里使用这个数据：

《PLoS One》2015年一篇题目为《Comparison of Two Hybrid Models for Forecasting the Incidence of Hemorrhagic Fever with Renal Syndrome in Jiangsu Province, China》文章的公开数据做演示。数据为江苏省2004年1月至2012年12月肾综合症出血热月发病率。运用2004年1月至2011年12月的数据预测2012年12个月的发病率数据。

首先，我们从最简单的决策树开始。建模是其次，主要是介绍时间序列预测的一些常见策略和方法。

二、时间序列预测的策略：单步滚动预测

（1）滞后期（lag）

假设我们有一组时间序列数据：1,2,3,4,5,6,7,8，这是一个由8个数字构成的序列。我们的目标是基于这个1至8的序列来预测接下来的6个数字，也就是9,10,11,12,13,14。

在机器学习建模的过程中，我们需要确定模型的“输入”和“输出”。因此，我们面临的首要问题是：在训练模型时，时间序列数据的输入和输出应该是什么？

这个问题可以被重新表述为：你计划使用前几个数字来预测下一个数字？

例如，如果我们选择使用一个数字来预测下一个数字，那么就会是1预测2，2预测3，以此类推。

输入	输出
1	2
2	3
3	4
...	...

或者，我们可以选择使用四个数字来预测下一个数字，那么就会是1,2,3,4预测5，2,3,4,5预测6。

输入	输出
1,2,3,4	5
2,3,4,5	6
3,4,5,6	7
...	...

简单来说，我们正在尝试从时间序列数据中分解出输入和输出，以便将其输入到模型中进行训练。这里的“一”和“四”被称为滞后期（lag），它们代表了我们用于预测的历史数据的长度。

因此，我们需要中Python干这件事：

使用的咒语：读取data.csv文件的数据，使用决策树建立一个时间序列预测模型。使用2004年1月至2011年12月的数据进行训练，采用2002年1月至2012年12月的数据作为验证集。滞后期（lag）暂时设置为6，也就是使用前6个数字预测地7个数值。决策树模型采用网格搜索进行参数寻优。

请一步一步进行，每一步运行好用保存好结果，我说继续，你再继续。

代码如下：

# 读取数据
import pandas as pd

data = pd.read_csv('data.csv')
data.head()

# 将时间列转换为日期格式
data['time'] = pd.to_datetime(data['time'], format='%b-%y')
# 显示转换后的前几行数据
data.head()

#拆分输入和输出
lag_period = 6

# 创建滞后期特征
for i in range(1, lag_period + 1):
    data[f'lag_{i}'] = data['incidence'].shift(i)

# 删除包含NaN的行
data = data.dropna().reset_index(drop=True)

看看输出：

原始数据被拆分成这种矩阵，大家仔细看肯定能看出规律，比如，对角线的数值都是一致的。

（2）数据集拆分

代码如下：

# 划分训练集和验证集
train_data = data[(data['time'] >= '2004-01-01') & (data['time'] <= '2011-12-31')]
validation_data = data[(data['time'] >= '2012-01-01') & (data['time'] <= '2012-12-31')]
train_data.shape, validation_data.shape
# 定义特征和目标变量
X_train = train_data[['lag_1', 'lag_2', 'lag_3', 'lag_4', 'lag_5', 'lag_6']]
y_train = train_data['incidence']
X_validation = validation_data[['lag_1', 'lag_2', 'lag_3', 'lag_4', 'lag_5', 'lag_6']]
y_validation = validation_data['incidence']
X_train.shape, X_validation.shape

但是，这其实有一个问题：验证集是不能用的。

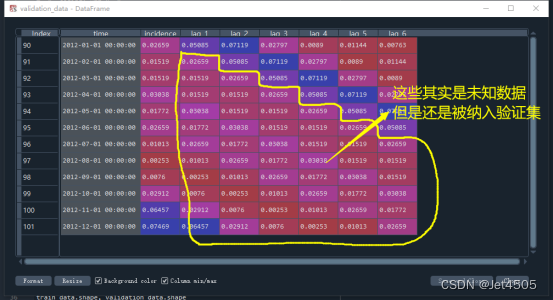
让我们以一个具体的例子来阐明另一个概念：

假设我们有一组时间序列数据：1,2,3,4,5,6,7,8，其中滞后期设定为3。

在训练集中，我们使用前三个数据点（1,2,3）来预测第四个数据点（4），然后使用（2,3,4）来预测第五个数据点（5），以此类推，直到使用（3,4,5）来预测第六个数据点（6）。

接下来，我们面临的问题是如何构建验证集。请注意，在这个阶段，我们只知道数据点1,2,3,4,5,6，而数据点7和8对我们来说是未知的。

首先，预测第七个数据点相对简单，我们可以使用已知的数据点（4,5,6）来预测7。但是，当我们尝试预测第八个数据点时，就会遇到问题。如果我们试图用（5,6,7）来预测8，问题在于，这里的7是未知的。

正确的做法应该是，首先使用（4,5,6）预测出一个估计的第七个数据点，记作7#。然后，我们再使用（5,6,7#）来预测第八个数据点。这个过程被称为滚动预测，希望这样的解释能帮助大家理解。

因此，划分的验证集，其实就第一行的数据可以用！

（3）建立模型和滚动预测

（3.1）决策树回归模型

#建立模型
from sklearn.tree import DecisionTreeRegressor
from sklearn.model_selection import GridSearchCV

# 初始化决策树模型
tree_model = DecisionTreeRegressor()

# 定义参数网格
param_grid = {
    'max_depth': [None, 3, 5, 7, 9],
    'min_samples_split': range(2, 11),
    'min_samples_leaf': range(1, 11)
}

# 初始化网格搜索
grid_search = GridSearchCV(tree_model, param_grid, cv=5, scoring='neg_mean_squared_error')

# 进行网格搜索
grid_search.fit(X_train, y_train)

# 获取最佳参数
best_params = grid_search.best_params_
best_params

import numpy as np
from sklearn.metrics import mean_absolute_error, mean_squared_error

# 使用最佳参数初始化决策树模型
best_tree_model = DecisionTreeRegressor(**best_params)

# 在训练集上训练模型
best_tree_model.fit(X_train, y_train)

解读：

（a）其实吧，也就是换了一个函数：DecisionTreeRegressor()；这个是决策树的回归函数，我们之前最分类用的是它的分类函数，仅此而已。

（b）其次，在拟合模型的时候：grid_search = GridSearchCV(tree_model, param_grid, cv=5, scoring='neg_mean_squared_error')，scoring换成均方误差的负值。为什么使用负值呢？因为GridSearchCV的默认行为是认为分数（score）越大越好，而对于均方误差来说，值越小表示模型越好。通过使用负值，我们可以使GridSearchCV在优化时选择最小的均方误差。其他可选的还有：

--neg_mean_squared_error: 负均方误差

--neg_mean_absolute_error: 负平均绝对误差

--neg_median_absolute_error: 负中位绝对误差

--r2: R^2（决定系数）

（3.2）滚动预测

看代码：

# 对于验证集，我们需要迭代地预测每一个数据点
y_validation_pred = []

for i in range(len(X_validation)):
    if i == 0:
        # 使用最后一个训练集的数据预测验证集的第一个数据点
        pred = best_tree_model.predict([X_validation.iloc[0]])
    else:
        # 使用前面预测出的数据构建新的特征，然后预测下一个数据点
        new_features = list(X_validation.iloc[i, 1:]) + [pred[0]]  # 将前面的特征向前移动，并使用上一次的预测作为最新的特征
        pred = best_tree_model.predict([new_features])
    y_validation_pred.append(pred[0])

y_validation_pred = np.array(y_validation_pred)

解读：

上面已经说了原理，这个只是代码实现。大家看注释，基本也看得懂了。

（4）模型评价

代码如下：

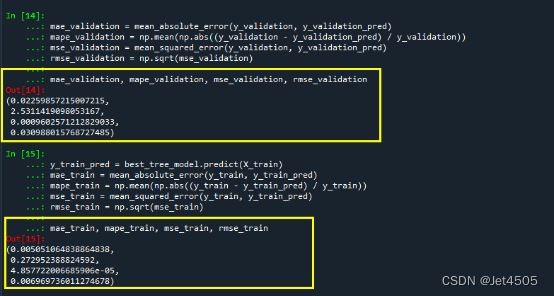
# 计算验证集上的MAE, MAPE, MSE和RMSE
mae_validation = mean_absolute_error(y_validation, y_validation_pred)
mape_validation = np.mean(np.abs((y_validation - y_validation_pred) / y_validation))
mse_validation = mean_squared_error(y_validation, y_validation_pred)
rmse_validation = np.sqrt(mse_validation)
mae_validation, mape_validation, mse_validation, rmse_validation

# 计算训练集上的MAE, MAPE, MSE和RMSE
y_train_pred = best_tree_model.predict(X_train)
mae_train = mean_absolute_error(y_train, y_train_pred)
mape_train = np.mean(np.abs((y_train - y_train_pred) / y_train))
mse_train = mean_squared_error(y_train, y_train_pred)
rmse_train = np.sqrt(mse_train)
mae_train, mape_train, mse_train, rmse_train

直接看结果吧：