一、卷积神经网络简介

在这里插入图片描述

卷积神经网络（Convolutional Neural Networks，简称CNN）是一种具有局部连接、权值共享等特点的深层前馈神经网络（Feedforward Neural Networks），是深度学习（deep learning）的代表算法之一，擅长处理图像特别是图像识别等相关机器学习问题，比如图像分类、目标检测、图像分割等各种视觉任务中都有显著的提升效果，是目前应用最广泛的模型之一。

卷积神经网络具有表征学习（representation learning）能力，能够按其阶层结构对输入信息进行平移不变分类（shift-invariant classification），可以进行监督学习和非监督学习，其隐含层内的卷积核参数共享和层间连接的稀疏性使得卷积神经网络能够以较小的计算量对格点化（grid-like topology）特征，例如像素和音频进行学习、有稳定的效果且对数据没有额外的特征工程（feature engineering）要求，并被大量应用于计算机视觉、自然语言处理等领域。

二、卷积神经网络的数学原理

计算机视觉中的图像是一种三维矩阵，三维矩阵中的大小是由图像的长、宽、深度决定的，长和宽容易理解，它们表征着像素点的个数；深度代表着几种颜色通道，我们所看到的彩色的图像都有红绿蓝三色光组成，就是R、G、B三种颜色通道组成，每个颜色通道数的取值范围为 $[0 ， 255]$ ，不同的RGB排列组合后可以构成 $2^{24}$ 种色彩

在这里插入图片描述

1、卷积层

卷积层由一组滤波器组成，滤波器为三维结构，一个滤波器可以看作由多个卷积核堆叠形成。这些滤波器在输入的图像数据上滑动做卷积运算，从输入数据中提取特征。在训练时，滤波器上的权重使用随机值进行初始化，并根据训练集进行学习，逐步优化。

卷积核是二维的权重矩阵，而滤波器（Filter）是多个卷积核堆叠而成的三维矩阵。卷积的运算方式就是从左往右、从上往下，选取图像中与卷积核大小一致的图像矩阵，按对应位进行乘积并求和，然后将所求和保存到输出的对应位置，接着按照滑动的步长，依据上述方式遍历整张图像，得到输出层

在这里插入图片描述

$Y_{i,j,k} = f\left(\sum_{m=0}^{C-1} \sum_{p=0}^{H_k-1} \sum_{q=0}^{W_k-1} X_{i+p, j+q, m} \cdot W_{p,q,m,k} + b_k\right)$

其中， $Y_{(i,j,k)}$ 表示输出特征图中位置 $(i, j)$ 上通道 k 的值， $X_{(i+p, j+q, m)}$ 表示输入特征图中位置 $(i + p, j + q)$ 上通道 $m$ 的值， $W_{p,q,m,k}$ 表示卷积核中位置 $(p, q)$ 上输入通道 $m$ 到输出通道 $k$ 的权重， $b_k$ 表示偏置项。ReLU是最常用的激活函数之一，由于其简单性和良好的性能，被广泛用于卷积神经网络中的卷积层。

卷积核的实质是一种特征提取算子，卷积能够更好提取区域特征，使用不同大小的卷积算子能够提取图像各个尺度的特征。类似人眼在处理视觉信号时，大脑皮层会先对视觉图像进行初步处理（大脑皮层某些细胞发现边缘和方向），接着再将事物抽象（大脑判定，眼前的物体的形状，是圆形的），最后在具象化（大脑进一步判定该物体是只气球）。通过卷积的运算，重要的特征的权值会越大，越有可能被提取出来。

2、池化层

池化层通常紧跟在卷积层之后，对卷积层输出的特征图进行下采样操作。常见的池化层包括平均池化和最大池化，通过采用最大值池化（Max Pooling）或平均值池化（Average Pooling）等操作，池化层可以从每个池化窗口中提取出最显著的特征值或特征平均值。这有助于保留图像中的主要特征，并降低对噪声或细节的敏感性。

通过池化操作，池化层可以减小特征图的空间尺寸，从而减少模型中的参数数量。这有助于降低计算复杂度，并减少过拟合的可能性。通过减小特征图的维度，模型可以更快地进行训练和推断。
在这里插入图片描述

$\max_{p, q} \left( x[i \cdot s + p, j \cdot s + q, k] \right)$

其中， $x$ 是输入特征图， $y$ 是池化后的输出特征图， $i$ 、 $j$ 和 $k$ 分别表示输出特征图的空间位置和通道索引， $s$ 是池化操作的步幅stride， $p$ 和 $q$ 是池化窗口内的位置索引。

无论物体在特征图上的位置如何变化，池化层可以保持对物体的检测或识别具有一定的不变性。这对于处理图像中的平移变化非常有用，因为物体的位置可能会发生变化，但它们的特征仍然是相似的。

3、感受野

感受野（Receptive Field）是指在输入数据上，卷积层中的一个神经元对应的输入区域大小。感受野的大小可以用来理解神经网络中神经元对输入数据的感知范围，就像人用眼睛观察外界，关注点不同视野会不一样。

感受野的大小取决于卷积层的结构，包括卷积核（Filter）的大小和步幅（Stride），以及之前层的结构。一般而言，感受野随着网络的层数增加而增大。

在一个卷积神经网络中，每个卷积层的感受野大小可以通过以下方式计算：

$\text{{Receptive Field}} = (\text{{Receptive Field of Previous Layer}} - 1) \times \text{{Stride}} + \text{{Filter Size}}$

在这里插入图片描述
其中，“Receptive Field of Previous Layer” 是上一层的感受野大小，“Stride” 是卷积操作的步幅，“Filter Size” 是当前卷积层的卷积核大小。

通过逐层计算，可以得到每个卷积层神经元的感受野大小。这个感受野大小表示了神经元对输入数据的局部信息感知范围。在深层网络中，感受野会逐渐增大，使得神经元可以捕捉到更广阔的上下文信息。

三、Python实战卷积神经网络

1、LetNet-5网络

LetNet-5网络包含两个卷积层、一个池化层和一个全连接层，先加载一下mnist手写数据集，接着构建网络框架，其中卷积核大小使用3x3矩阵，激活函数使用Relu，最大池化窗口使用2x2矩阵，调用dropout方法降低模型复杂度，然后在输出层用softmax函数映射图像属于每个类别的概率，最后在编译网络时设定分类交叉熵损失函数和优化器类别，最后开始训练

import keras
import tensorflow as tf
from keras.datasets import mnist
from keras.models import Sequential
from keras.layers import Dense, Dropout
from tensorflow.keras.optimizers import SGD
from keras.layers import Conv2D, MaxPooling2D, Flatten
import matplotlib.pyplot as plt

(X_train, y_train), (X_valid, y_valid) = mnist.load_data()
n_classes = 10
y_train = tf.squeeze(y_train)
y_train = tf.one_hot(y_train, depth=10)
y_valid = tf.squeeze(y_valid)
y_valid = tf.one_hot(y_valid, depth=10)

X_train = X_train.reshape(60000, 28, 28, 1).astype('float32')
X_valid = X_valid.reshape(10000, 28, 28, 1).astype('float32')

model = Sequential()
model.add(Conv2D(32, kernel_size=(3, 3), activation='relu', input_shape=(28, 28, 1)))

model.add(Conv2D(64, kernel_size=(3, 3), activation='relu'))
model.add(MaxPooling2D(pool_size=(2, 2)))
model.add(Dropout(0.25))
model.add(Flatten())

model.add(Dense(128, activation='relu'))
model.add(Dropout(0.4))

model.add(Dense(n_classes, activation="softmax"))

model.compile(optimizer='adam',
              loss='categorical_crossentropy',
              metrics=['accuracy'])
history = model.fit(X_train, y_train, batch_size=32, epochs=10, validation_data=(X_valid, y_valid))


#C:\python3.11\python.exe C:\Users\11863\Documents\Python机器学习\卷积神经网络\venv\AlexNet.py 

1875/1875 [==============================] - 52s 27ms/step - loss: 0.4479 - accuracy: 0.9172 - val_loss: 0.0770 - val_accuracy: 0.9750

2、Resnet 残差网络

残差网络（Residual Network，通常缩写为 ResNet）是一种深度学习神经网络架构，旨在解决深度神经网络训练过程中的梯度消失和梯度爆炸问题。

在传统的神经网络中，通过堆叠多个层来构建深度网络，但当网络变得更深时，训练过程变得更加困难。梯度消失和梯度爆炸是由于层间信息传递时的退化问题，导致训练过程难以收敛或效果不佳。

残差网络通过引入“残差块”（Residual Block）的概念来解决这个问题。在残差块中，输入与输出之间添加了一个“跳跃连接”（Skip Connection），允许信息在不同层之间直接传递。这个跳跃连接绕过了一些层，将输入的信息直接添加到输出中，形成了一个残差映射（Residual Mapping）

在这里插入图片描述
其中， $x$ 表示的是输入的特征矩阵；网络主路的输出 $F (x)$ 是残差函数；网络的支路就是我们所说的捷径连接（Shortcut Connection），其中 $x i d e n t i t y$ 表示的是恒等映射，也就是：直接将输入的特征矩阵 $x$ 本身跳层传递到输出。直接将主路和支路输出相加得： $H (x) = F (x) + x$ ，最后再加上一个 $re l u$ 激活函数就得到残差模块的输出

Python封装残差模块思路也很简单，先封装卷积层，卷积层包括卷积核、归一化、Relu激活函数，再封装残差模块，两个卷积层形成的残差计算和一个卷积层的同等映射，最后加和一起输出

from tensorflow.keras.layers import Conv2D, BatchNormalization, Activation, Add


def Conv_BN_Relu(filters, kernel_size, strides, input_layer):
    x = Conv2D(filters, kernel_size, strides=strides, padding='same')(input_layer)
    x = BatchNormalization()(x)
    x = Activation('relu')(x)
    return x


# ResNet18网络对应的残差模块a和残差模块b
def resiidual_a_or_b(input_x, filters, flag):
    if flag == 'a':
        # 主路
        x = Conv_BN_Relu(filters, (3, 3), 1, input_x)
        x = Conv_BN_Relu(filters, (3, 3), 1, x)
    
        # 输出
        y = Add()([x, input_x])

        return y
    elif flag == 'b':
        # 主路
        x = Conv_BN_Relu(filters, (3, 3), 2, input_x)
        x = Conv_BN_Relu(filters, (3, 3), 1, x)

        # 支路下采样
        input_x = Conv_BN_Relu(filters, (1, 1), 2, input_x)

        # 输出
        y = Add()([x, input_x])

        return y

3、VGGNet 迁移学习

迁移学习（Transfer Learning）是指将在一个任务上训练好的模型的知识（通常是权重参数）应用到另一个相关任务上的技术。在卷积神经网络中，迁移学习可以通过以下方式应用：

微调全连接层：将预训练的卷积神经网络模型应用于新任务时，可以保持底层卷积层的权重不变，只训练顶部的全连接层。这是因为底层卷积层学习到的特征提取器通常具有较好的通用性，可以迁移到新任务中。通过仅训练顶部的全连接层，可以快速适应新任务的特定需求。

转移卷积层特征：除了微调全连接层，还可以将预训练的卷积层的特征输出作为新任务的输入。即保持卷积层的权重不变，将其作为特征提取器，然后在顶部添加新的全连接层或其他结构，用于新任务的分类或回归。这种方法特别适用于新任务与预训练任务具有相似的特征表示需求的情况。

迁移学习的主要优势在于它可以通过利用预训练模型的参数和特征表示来加快新任务的训练过程，尤其在数据集较小或相似性较高的情况下表现良好。它可以减少训练时间和数据需求，并提高模型的泛化能力。通过迁移学习，可以从一个任务中学习到的知识迁移到另一个任务上，从而加速模型的收敛和提高性能。

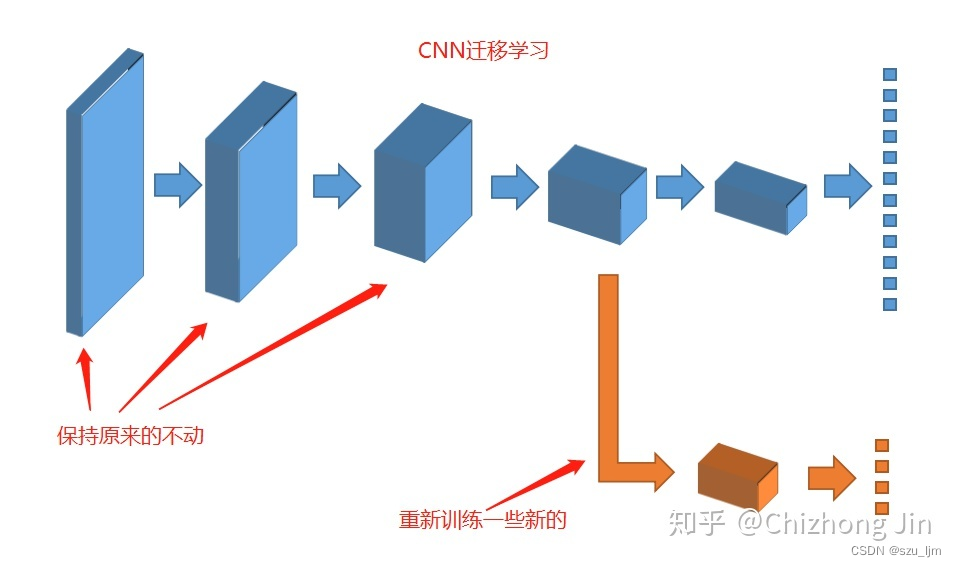
在这里插入图片描述
下面我们借助预训练好的VGG19模型进行迁移学习，将VGG19的网络架构嵌入自己的CNN网络中，只需要再经过少量数据训练即可到达比较好的效果。在网络结构最后加入softmax层并进行剪枝，输出图像分类的概率

from keras.applications.vgg19 import VGG19
from keras.models import Sequential
from keras.layers import Dense, Dropout, Flatten
from keras.preprocessing.image import ImageDataGenerator
from keras.datasets import cifar10
import tensorflow as tf

(X_train, y_train), (X_valid, y_valid) = cifar10.load_data()
n_classes = 10

X_train = X_train.astype('float32')
X_valid = X_valid.astype('float32')


vgg19 = VGG19(include_top=False, weights='imagenet', input_shape=(32, 32, 3), pooling=None)

for layer in vgg19.layers:
    layer.trainable = False

model = Sequential()
model.add(vgg19)

model.add(Flatten(name='flattened'))
model.add(Dropout(0.5, name='dropout'))
model.add(Dense(2, activation='softmax', name='predictions'))

model.compile(optimizer='adam', loss='categorical_crossentropy', metrics=['accuracy'])
history = model.fit(X_train, y_train, batch_size=32, epochs=10, validation_data=(X_valid, y_valid))