一)位图:

首先计算一下存储一下10亿个整形数据，需要多大内存呢，多少个G呢？

2^30=10亿，10亿个字节

byte kb mb gb

100000000个字节/1024/1024/1024=1G

所以10亿个字节就是1G，所以40亿个字节就是4G，也就是10个整形数据

给定40亿个不重复的无符号整数，没有排过序，给定一个无符号整数，如何可以快速地判断出一个数是否在这40亿个数中？

解法1:哈希表，10亿个字节，大概是1G，一个int型占4字节，10亿就是40亿字节很明显就是4GB，也就是如果完全读入内存需要占用4GB，40亿个整数是16G，一般运行内存存不下，所以说使用哈希表进行遍历时间复杂度是O(N)

解法2:排序+二分查找，O(N+logN)，内存也是存不下的，二分查找必须是在内存中进行二分查找

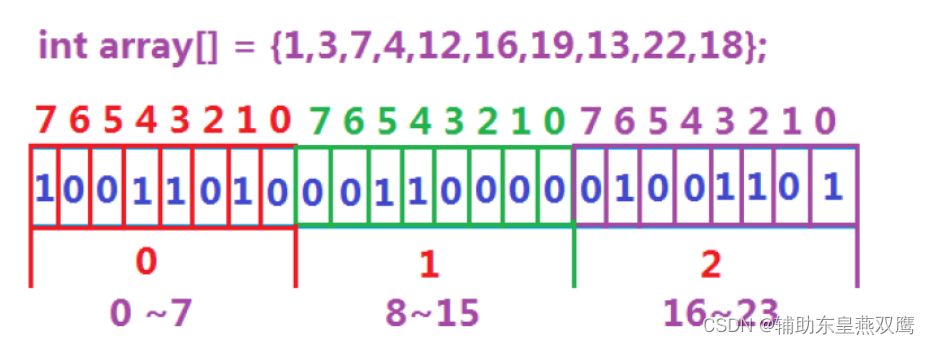
解法3:位图，假设40亿个数据放到了40亿个比特位里面，2^32=40个亿，40亿除8等于X字节，X字节/1024=YKB，YKB/1024=ZMB=512M，1个位占用一个数据，所以仅仅使用512M内存就可以把这些数据全部存储起来，位图有的资料也称之为是bitMap

1)数据是否在给定的整形数据中恰好是在与不在，刚好是两种状态，那么此时就可以使用一个二进制比特位来代表数据是否存在的信息，如果二进制比特位为1，那么代表存在，为0表示不存在，比如说下面这个例子

2)array[index]/8确定的是在那一段区间

array[index]%8确定在那一段区间的哪一个位置

3)也可以很方便进行排序:从左到右输出二进制比特位是1的数据，但是有多个重复的数字就不好处理了，所以位图适用于整形况且没有重复的数据

4)所谓位图，就是用每一位来存放某种状态，适用于海量数据，整数，数据无重复的场景。通常是用来判断某个数据存不存在的

5)位图天然是可以去重的，JAVA当中有一个类叫做BitMap，也叫做位图，也是JAVA.util的类，BitMap底层实现的是long[]，但是我们所实现的是byte[]数组，是用于快速查找某一个元素是否存在，况且还可以节省空间；

import java.util.Arrays;

public class MyBitSet {
    public byte[] array;
    //每一个字节的比特位数都是从左到右边依次递增的
    public int usedSize;//记录在当前这个位图中存放了多少有效的数据
    public MyBitSet(){
        this.usedSize=0;
        this.array=new byte[1];
    }
    //这里面的n表示需要多少个比特位,有可能会多给1个字节,但是也是无所谓的
    public MyBitSet(int n){
        this.array=new byte[n/8+1];//假设n=12,此时实际上计算是1个字节,其实现在给2个字节也是可以的
        this.usedSize=0;
    }
    //设置某一位是1
    public void set(int val){
        if(val<0) throw new ArrayIndexOutOfBoundsException();
        int arrayIndex=val/8;//先找到这个数要放到第几个字节
        if(arrayIndex>array.length-1){
            //等于的时候刚刚好
          this.array= Arrays.copyOf(array,arrayIndex+1);
          //数组如果越界,那么直接进行扩容,假设存放130,那么计算的下标是16,那么扩容到17个个字节即可
        }
        int bitIndex=val%8;//再找到要修改这个字节的第几位
        //也就是说我们要把array[arrayIndex]的第bitIndex位设置成1
        this.array[arrayIndex]|=(1<<bitIndex);
        usedSize++;
    }
    //判断当前位是不是1
    public boolean get(int val){//判断当前val存储的这一位是1还是0
        if(val<0) throw new ArrayIndexOutOfBoundsException();
        int arrayIndex=val/8;
        if(arrayIndex>array.length-1) return false;
        int bitIndex=val%8;
        if(((array[arrayIndex]>>bitIndex)&1)==1) return true;//if((array[array[index]&(1<<bitIndex))!=0)
        return false;
    }
    //将val对应字节的存储对应位置置为0,就是相当于是在位图中删除这个值
    public void reset(int val){
        if(val<0) throw new ArrayIndexOutOfBoundsException();
        int arrayIndex=val/8;
        int bitIndex=val%8;
        usedSize--;
        array[arrayIndex]= (byte) ((~(1<<bitIndex))&array[arrayIndex]);
    }
    public int getUsedSize(){
        return usedSize;//返回当前位图中所存储的元素个数
    }
    //根据位图来进行排序

    public static void main(String[] args) {
        int[] nums={1,9,8,78,100,20,45,16};
        MyBitSet set=new MyBitSet(20);
        //1.现将所有的数字存放到位图里面
        for(int i=0;i<nums.length;i++){
            set.set(nums[i]);
            System.out.println(set.get(nums[i]));
        }
        System.out.println(set.getUsedSize());
        //2.从小到大遍历所有的字节,遍历到其中一个字节之后在进行按照下标从小到大遍历每一个字节里面的比特位
        for(int i=0;i<set.array.length;i++){
            for(int j=0;j<8;j++){
                if(((set.array[i])&(1<<j))!=0){
                    System.out.println(i*8+j);
                }
            }
        }
    }

}

二)布隆过滤器:哈希和位图的一个整合

布隆过滤器的提出:日常生活中在我们进行设计计算机软件的时候，通常要进行判断某一个元素是否在集合中，最直接的方法就是将所有的元素存储到一个哈希表中，当遇到一个新元素的时候，要进行判断当前这个元素是否出现在集合中

1)在布隆过滤器中最终并没有我所需要进行判断的值

2)布隆过滤器是一种比较巧妙的，紧凑型的概率性数据结构，特点是高效的插入和查询，可以用来告诉你某一样东西一定不存在或者是可能存在，它的原理是使用多个哈希函数，将一个数据映射到位图结构中，此种方式不仅仅可以提升查询效率，也是可以进行节省大量的内存空间，下面是类似与布隆过滤器的插入