摘要:傅里叶变换可以将任何满足相应数学条件的信号转换为不同系数的简单正弦和余弦函数的和。图像信号也是一种信号,只不过是二维离散信号,通过傅里叶变换对图像进行变换可以图像存空域转换为频域进行更多的处理。本文主要简要描述傅里叶变换以及其在图像处理中的简单应用,并进行一些简单的实验来描述其相关性质。
关键字:傅里叶变换,二维傅里叶变换,二维离散傅里叶变换
傅里叶变换是对傅里叶级数进行研究得到的结论,傅里叶发现满足一定数学条件的复杂周期函数可以用一系列简单的正弦和余弦函数之和表示。分解后的表示形式的每个分量都是一个频率的分量,也就将复杂信号转换成简单信号,而简单信号更容易进行数学描述和分析。
1 复数域
由于傅里叶变换中涉及到了复数,首先简单了解下复数。
复数的定义如下:
C
=
R
+
j
I
C=R+jI
C=R+jI
其中
R
R
R和
I
I
I都为实数分别为复数的实部和虚部,而
j
j
j是-1的平方根,即
j
2
=
−
1
j^2=-1
j2=−1。实数集就是我们一般谈的数集,其实复数的子集(当
I
=
0
I=0
I=0时)。如果需要在平面坐标中表述复数,其实和普通的笛卡尔坐标系表示相同,只是横坐标换成实数,纵坐标换成虚数即可(即复数是复平面坐标中的点
(
R
,
I
)
(R,I)
(R,I))。
复数的共轭:
C
∗
=
R
−
j
I
C^{*}=R-jI
C∗=R−jI
复数在极坐标下的表示为:
C
=
∣
C
∣
(
c
o
s
θ
+
j
s
i
n
θ
)
∣
C
∣
=
R
2
+
I
2
θ
=
a
r
c
t
a
n
(
I
R
)
\begin{equation} \begin{aligned} C&=|C|(cos\theta+jsin\theta)\\ |C|&=\sqrt{R^2+I^2}\\ \theta&=arctan(\frac{I}{R}) \end{aligned} \end{equation}
C∣C∣θ=∣C∣(cosθ+jsinθ)=R2+I2=arctan(RI)
另外如果用欧拉公式转(
e
j
θ
=
c
o
s
θ
+
j
s
i
n
θ
e^{j\theta=cos\theta+jsin\theta}
ejθ=cosθ+jsinθ)换则可以转换为:
C
=
∣
C
∣
e
j
θ
C=|C|e^{j\theta}
C=∣C∣ejθ
2 傅里叶变换
2.1 傅里叶级数
傅里叶级数:即具有周期
T
T
T的连续变换
t
t
t的周期函数
f
(
t
)
f(t)
f(t)可以被描述为乘以适合的系数的正弦和余弦的和,这个和就是傅里叶级数。
f
(
t
)
=
∑
n
=
−
∞
∞
c
n
e
j
2
π
n
T
t
c
n
=
1
T
∫
−
T
2
T
2
f
(
t
)
e
−
j
2
π
n
T
t
d
t
,
n
=
0
,
±
1
,
±
2
,
.
.
.
\begin{equation} \begin{aligned} f(t)&=\sum_{n=-\infty}^{\infty}{c_{n}e^{j\frac{2\pi n}{T}t}}\\ cn&=\frac{1}{T}\int_{-\frac{T}{2}}^{\frac{T}{2}}{f(t)e^{-j\frac{2\pi n}{T}t}}dt,n=0,\pm1,\pm2,... \end{aligned} \end{equation}
f(t)cn=n=−∞∑∞cnejT2πnt=T1∫−2T2Tf(t)e−jT2πntdt,n=0,±1,±2,...
使用欧拉公式转换即可得到正弦和余弦和的标识:
f
(
t
)
=
∑
n
=
−
∞
∞
c
n
[
c
o
s
(
2
π
n
T
t
)
+
j
s
i
n
(
2
π
n
T
t
)
]
f(t)=\sum_{n=-\infty}^{\infty}{c_{n}[cos(\frac{2\pi n}{T}t)+jsin(\frac{2\pi n}{T}t)]}
f(t)=n=−∞∑∞cn[cos(T2πnt)+jsin(T2πnt)]
假设原始波形的为
f
(
t
)
=
f
(
t
+
T
)
f(t)=f(t+T)
f(t)=f(t+T),则对于傅里叶级数而言,其n次谐波(当
n
=
1
n=1
n=1时的分量为一次谐波,
n
=
2
n=2
n=2时的分量为二次谐波)的幅度为
c
n
c_n
cn,周期为
T
n
\frac{T}{n}
nT,频率为
n
T
\frac{n}{T}
Tn。
2.2 连续傅里叶变换
一维连续傅里叶变换
满足狄利克雷条件的函数
f
(
t
)
f(t)
f(t)的傅里叶变换为:
狄利克雷条件:
- 在一周期内,连续或只有有限个第一类间断点;
- 在一周期内,极大值和极小值的数目应是有限个;
- 在一周期内,信号是绝对可积的。
F
(
μ
)
=
∫
−
∞
+
∞
f
(
t
)
e
−
j
2
π
μ
t
d
t
F
(
μ
)
=
∫
−
∞
+
∞
f
(
t
)
[
c
o
s
(
2
π
μ
t
)
−
j
s
i
n
(
2
π
μ
t
)
]
d
t
μ
=
n
T
\begin{equation} \begin{aligned} F(\mu)&=\int_{-\infty}^{+\infty}{f(t)e^{-j2\pi \mu t}dt}\\ F(\mu)&=\int_{-\infty}^{+\infty}{f(t)[cos(2\pi \mu t) - jsin(2\pi \mu t)]dt}\\ \mu&=\frac{n}{T} \end{aligned} \end{equation}
F(μ)F(μ)μ=∫−∞+∞f(t)e−j2πμtdt=∫−∞+∞f(t)[cos(2πμt)−jsin(2πμt)]dt=Tn
F
(
t
)
F(t)
F(t)傅里叶变换对应的傅里叶逆变换
F
−
1
(
t
)
F^{-1}(t)
F−1(t)为:
f
(
t
)
=
∫
−
∞
+
∞
F
(
μ
)
e
j
2
π
μ
t
d
μ
f
(
t
)
=
∫
−
∞
+
∞
F
(
μ
)
[
c
o
s
(
2
π
μ
t
)
+
j
s
i
n
(
2
π
μ
t
)
]
d
μ
μ
=
n
T
\begin{equation} \begin{aligned} f(t)&=\int_{-\infty}^{+\infty}{F(\mu)e^{j2\pi \mu t}d\mu}\\ f(t)&=\int_{-\infty}^{+\infty}{F(\mu)[cos(2\pi \mu t) + jsin(2\pi \mu t)]d\mu}\\ \mu&=\frac{n}{T} \end{aligned} \end{equation}
f(t)f(t)μ=∫−∞+∞F(μ)ej2πμtdμ=∫−∞+∞F(μ)[cos(2πμt)+jsin(2πμt)]dμ=Tn
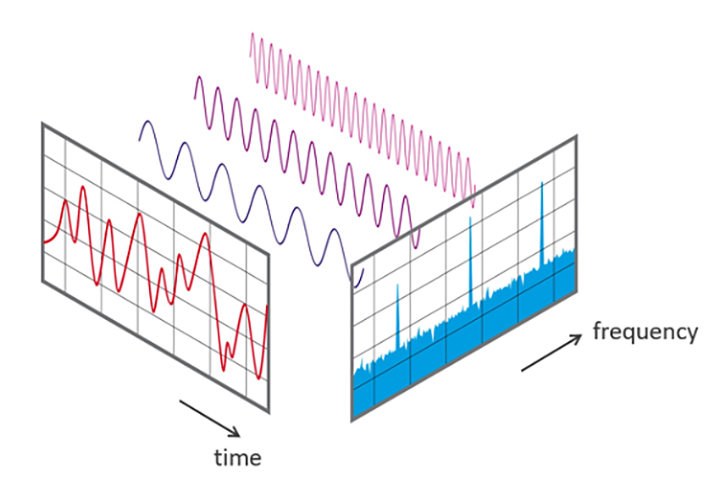
傅里叶变换 F ( t ) F(t) F(t)可以将连续函数 f ( t ) f(t) f(t)从时域转换到频域空间,而逆变换 F − 1 ( t ) F^{-1}(t) F−1(t)可以将其傅里叶变换 F ( t ) F(t) F(t)还原到时域得到 f ( t ) f(t) f(t)。傅里叶变换和傅里叶逆变换构成傅里叶变换对。通常的信号处理,如果在时域不好处理时,我们可以利用傅里叶变换先将信号转换到频域,在频域空间进行处理之后再用逆变换将信号转换到时域空间。
二维连续傅里叶变换
二维傅里叶变换和一维傅里叶变换类似,只是将一维扩展到二维:
F
(
μ
,
v
)
=
∫
−
∞
+
∞
∫
−
∞
+
∞
f
(
t
,
z
)
e
−
j
2
π
(
μ
t
+
v
z
)
d
t
d
z
f
(
t
,
z
)
=
∫
−
∞
+
∞
∫
−
∞
+
∞
F
(
μ
,
v
)
e
j
2
π
(
μ
t
+
v
z
)
d
μ
d
v
μ
=
n
T
μ
,
v
=
n
T
v
\begin{equation} \begin{aligned} F(\mu,v)&=\int_{-\infty}^{+\infty}\int_{-\infty}^{+\infty}{f(t,z)e^{-j2\pi(\mu t + vz)}dt dz}\\ f(t,z)&=\int_{-\infty}^{+\infty}\int_{-\infty}^{+\infty}{F(\mu,v)e^{j2\pi(\mu t + vz)}d\mu dv}\\ \mu&=\frac{n}{T_{\mu}},v=\frac{n}{T_{v}} \end{aligned} \end{equation}
F(μ,v)f(t,z)μ=∫−∞+∞∫−∞+∞f(t,z)e−j2π(μt+vz)dtdz=∫−∞+∞∫−∞+∞F(μ,v)ej2π(μt+vz)dμdv=Tμn,v=Tvn
傅里叶变换后是在复数空间,即
F
(
u
)
=
R
(
μ
)
+
j
I
(
μ
)
=
∣
F
(
μ
)
∣
e
j
ϕ
(
u
)
F(u)=R(\mu)+jI(\mu)=|F(\mu)|e^{j\phi(u)}
F(u)=R(μ)+jI(μ)=∣F(μ)∣ejϕ(u)
傅里叶谱:
∣
F
(
μ
)
∣
=
∣
R
(
μ
)
2
+
I
(
μ
)
2
∣
1
2
|F(\mu)|=|R(\mu)^2+I(\mu)^2|^{\frac{1}{2}}
∣F(μ)∣=∣R(μ)2+I(μ)2∣21;
相角:
ϕ
(
μ
)
=
a
r
c
t
h
a
n
(
I
(
μ
)
R
(
μ
)
)
\phi(\mu)=arcthan(\frac{I(\mu)}{R(\mu)})
ϕ(μ)=arcthan(R(μ)I(μ));
能量谱:
P
(
u
)
=
∣
F
(
μ
)
∣
2
=
R
(
μ
)
2
+
I
(
μ
)
2
P(u)=|F(\mu)|^2=R(\mu)^2+I(\mu)^2
P(u)=∣F(μ)∣2=R(μ)2+I(μ)2。
2.3 离散傅里叶变换
实际使用时由于硬件设备的原因,我们只能对离散数据进行处理,而离散数据是通过采样得到的。
2.3.1 卷积
在了解如何对连续信号进行取样的傅里叶变换之前先了解下卷积能够方面我们进行后续的处理。
卷积本质就是将两个信号相乘做积分,但是如果只是简单相乘则得到的输出值当
f
(
t
)
f(t)
f(t)为冲激函数时,输出值和相乘的函数
h
(
t
)
h(t)
h(t)相反。因此需要将
h
(
t
)
h(t)
h(t)关于原点做反转。于是卷积的定义为:
f
(
t
)
∗
h
(
t
)
=
∫
−
∞
+
∞
f
(
τ
)
h
(
t
−
τ
)
d
τ
f(t)\ast h(t)=\int_{-\infty}^{+\infty}f(\tau)h(t-\tau)d\tau
f(t)∗h(t)=∫−∞+∞f(τ)h(t−τ)dτ
而卷积对应的傅里叶变换为(
F
(
μ
)
F(\mu)
F(μ)和
H
(
μ
)
H(\mu)
H(μ)分别为两个函数的傅里叶变换):
F
(
f
(
t
)
∗
h
(
t
)
)
=
∫
−
∞
+
∞
[
∫
−
∞
+
∞
f
(
τ
)
h
(
t
−
τ
)
d
τ
]
e
e
−
j
2
π
τ
d
t
=
H
(
μ
)
F
(
μ
)
F(f(t)\ast h(t))=\int_{-\infty}^{+\infty}[\int_{-\infty}^{+\infty}f(\tau)h(t-\tau)d\tau]e^{e^{-j2\pi \tau}}dt=H(\mu)F(\mu)
F(f(t)∗h(t))=∫−∞+∞[∫−∞+∞f(τ)h(t−τ)dτ]ee−j2πτdt=H(μ)F(μ)
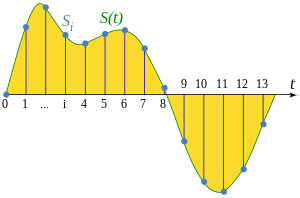
2.3.2 取样
假设对于连续函数
f
(
t
)
f(t)
f(t),对独立变量
t
t
t以
Δ
T
\Delta T
ΔT的间隔进行取样,并记采样得到的离散信号为
f
^
(
t
)
\hat{f}(t)
f^(t),则
f
^
(
t
)
=
f
(
t
)
s
Δ
T
(
t
)
=
∑
n
=
−
∞
+
∞
f
(
t
)
δ
(
t
−
n
Δ
T
)
\hat{f}(t)=f(t)s_{\Delta T}(t)=\sum_{n=-\infty}^{+\infty}f(t)\delta(t - n\Delta T)
f^(t)=f(t)sΔT(t)=n=−∞∑+∞f(t)δ(t−nΔT)
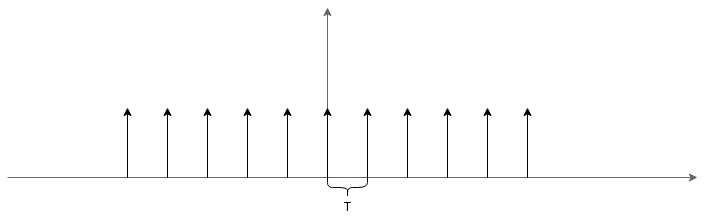
其中
s
Δ
T
(
t
)
s_{\Delta T}(t)
sΔT(t)为冲激串:
而取样冲激串的傅里叶变换为:
S
(
μ
)
=
S
(
δ
(
t
−
n
Δ
T
)
)
=
1
Δ
T
∑
n
=
−
∞
+
∞
δ
(
μ
−
n
Δ
T
)
\begin{equation} \begin{aligned} S(\mu)&=S(\delta(t - n\Delta T))=\frac{1}{\Delta T}\sum_{n=-\infty}^{+\infty}\delta(\mu - \frac{n}{\Delta T}) \end{aligned} \end{equation}
S(μ)=S(δ(t−nΔT))=ΔT1n=−∞∑+∞δ(μ−ΔTn)
则采样后的离散序列的傅里叶变换为:
F
(
f
^
(
t
)
)
=
F
[
f
(
t
)
s
Δ
T
(
t
)
]
=
F
(
μ
)
∗
S
(
μ
)
=
1
Δ
T
∑
n
=
−
∞
+
∞
F
(
μ
−
n
Δ
T
)
F(\hat{f}(t))=F[f(t)s_{\Delta T}(t)]=F(\mu)\ast S(\mu)=\frac{1}{\Delta T}\sum_{n=-\infty}^{+\infty}F(\mu - \frac{n}{\Delta T})
F(f^(t))=F[f(t)sΔT(t)]=F(μ)∗S(μ)=ΔT1n=−∞∑+∞F(μ−ΔTn)
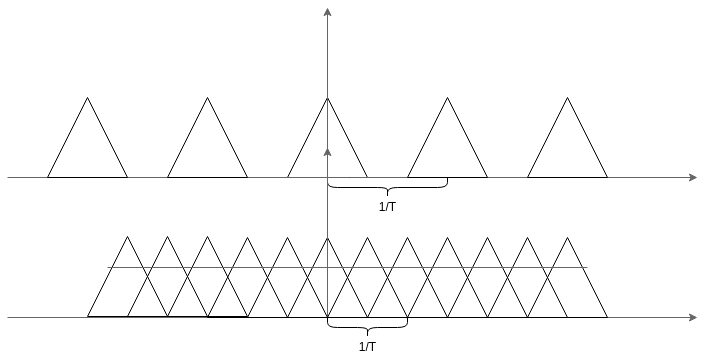
从上面的式子中我们能够看到采样后的离散信号的傅里叶变换就是原始信号的傅里叶变换的无穷拷贝,而每个拷贝之间的间隔为采样频率,即
1
Δ
T
\frac{1}{\Delta T}
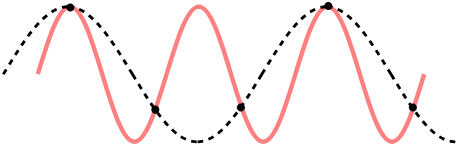
ΔT1。如果采样频率过低,则采样信号的相邻两个傅里叶变换就会重叠,发生混叠无法区分,采样得到的信号就会失真。因此采样频率的下限为
1
2
Δ
T
\frac{1}{2\Delta T}
2ΔT1,即奈奎斯特采样频率,如果低于这个频率采样就会失真,高于这个频率采样基本能还原出原始信号。
下图的虚线就是使用低采样频率采样失真的效果:
2.3.3 离散傅里叶变换
一维离散傅里叶变换
经过采样的离散函数
f
^
(
t
)
的
\hat{f}(t)的
f^(t)的离散傅里叶变换的表示为:
F
^
(
μ
)
=
∫
−
∞
+
∞
f
^
(
t
)
e
−
j
2
π
μ
t
d
t
=
∫
−
∞
+
∞
∑
n
=
−
∞
+
∞
f
(
t
)
δ
(
t
−
n
Δ
T
)
e
−
j
2
π
μ
t
d
t
=
∑
n
=
−
∞
+
∞
∫
−
∞
+
∞
f
(
t
)
δ
(
t
−
n
Δ
T
)
e
−
j
2
π
μ
t
d
t
=
∑
n
=
−
∞
+
∞
f
n
e
−
j
2
π
μ
Δ
T
\begin{equation} \begin{aligned} \hat{F}(\mu)&=\int_{-\infty}^{+\infty}{\hat{f}(t)e^{-j2\pi \mu t}dt}\\ &=\int_{-\infty}^{+\infty}{ \sum_{n=-\infty}^{+\infty}f(t)\delta(t - n\Delta T) e^{-j2\pi \mu t} }dt\\ &=\sum_{n=-\infty}^{+\infty} \int_{-\infty}^{+\infty}{f(t)\delta(t - n\Delta T) e^{-j2\pi \mu t} }dt\\ &=\sum_{n=-\infty}^{+\infty} f_{n}e^{-j2\pi \mu \Delta T} \end{aligned} \end{equation}
F^(μ)=∫−∞+∞f^(t)e−j2πμtdt=∫−∞+∞n=−∞∑+∞f(t)δ(t−nΔT)e−j2πμtdt=n=−∞∑+∞∫−∞+∞f(t)δ(t−nΔT)e−j2πμtdt=n=−∞∑+∞fne−j2πμΔT
由于
F
^
(
t
)
\hat{F}(t)
F^(t)是周期为
1
Δ
T
\frac{1}{\Delta T}
ΔT1的无线周期连续函数,因此我们只需要关心一个周期内的FT状态即可。假设我们在一个周期内得到
F
^
(
t
)
\hat{F}(t)
F^(t)的
M
M
M个等距采样的样本,那么
μ
=
m
M
Δ
T
,
m
=
0
,
1
,
.
.
.
,
M
−
1
\mu=\frac{m}{M\Delta T},m=0,1,...,M-1
μ=MΔTm,m=0,1,...,M−1,即
F
^
(
m
)
=
∑
m
=
0
M
−
1
f
n
e
−
j
2
π
m
n
/
M
,
m
=
0
,
1
,
2
,
.
.
.
,
M
−
1
\hat{F}(m)=\sum_{m=0}^{M-1}f_ne^{-j2\pi mn/M},m=0,1,2,...,M-1
F^(m)=m=0∑M−1fne−j2πmn/M,m=0,1,2,...,M−1
相对的,当我们知道傅里叶变换为
F
^
(
t
)
\hat{F}(t)
F^(t)时,即可通过逆变换得到对应的离散信号:
f
^
(
n
)
=
1
M
∑
m
=
0
M
−
1
F
m
e
j
2
π
m
n
/
M
,
m
=
0
,
1
,
2
,
.
.
.
,
M
−
1
\hat{f}(n)=\frac{1}{M}\sum_{m=0}^{M-1}F_me^{j2\pi mn/M},m=0,1,2,...,M-1
f^(n)=M1m=0∑M−1Fmej2πmn/M,m=0,1,2,...,M−1
二维离散傅里叶变换
首先我们将上面提到的一维离散傅里叶变换扩展到二维空间:
F
^
(
u
,
v
)
=
∑
x
=
0
M
−
1
∑
y
=
0
N
−
1
f
(
x
,
y
)
e
−
j
2
π
(
u
x
M
+
v
y
N
)
f
^
(
x
,
y
)
=
1
M
N
∑
x
=
0
M
−
1
∑
y
=
0
N
−
1
F
(
u
,
v
)
e
j
2
π
(
u
x
M
+
v
y
N
)
\begin{equation} \begin{aligned} \hat{F}(u,v)&=\sum_{x=0}^{M-1}\sum_{y=0}^{N-1}f(x,y)e^{-j2\pi(\frac{ux}{M} + \frac{vy}{N})}\\ \hat{f}(x,y)&=\frac{1}{MN}\sum_{x=0}^{M-1}\sum_{y=0}^{N-1}F(u,v)e^{j2\pi(\frac{ux}{M} + \frac{vy}{N})} \end{aligned} \end{equation}
F^(u,v)f^(x,y)=x=0∑M−1y=0∑N−1f(x,y)e−j2π(Mux+Nvy)=MN1x=0∑M−1y=0∑N−1F(u,v)ej2π(Mux+Nvy)
二维离散信号是由二维连续函数采样得到,即数字图像是从真实世界采集光信号转换成电信号,由于硬件器件的原因肯定存在精度问题。数字图像是有限时间信号,而有限时间信号包含无限频率,所以无法从采样函数的傅里叶变换中分离出一个完整的原函数的傅里叶变换。因此数字图像总是存在混淆的问题,只是不同精度问题严重程度不同。当采样率足够高时该问题人眼几乎不可察觉。
混叠是指取样讯号被还原成连续讯号时产生彼此交叠而失真的现象。
3 傅里叶变换的实现
3.1 DCT
傅里叶变换的实现比较简单,暴力时间复杂度为
O
(
n
4
)
\Omicron(n^4)
O(n4)。代码中的Matrix是自己实现的矩阵类基本操作就是一般矩阵的操作。#pragma omp parallel for是打开了OMP加速。
template<int, class T>
static Matrix<double> dft(const Matrix<T> &m){
GASSERT(m.channels() == 1, "the matrix channle must be 1");
std::size_t hei = m.rows(), wid = m.cols();
Matrix<double> dftm(m.cols(), m.rows(), 2);
#pragma omp parallel for
for(std::size_t u = 0; u < hei; u ++){
for(std::size_t v = 0; v < wid; v ++){
double rv = 0.0, vv = 0.0;
for(std::size_t y = 0; y < hei; y ++){
for(std::size_t x = 0; x < wid; x ++){
double xv = 2.0 * M_PI * (u * y * 1.0/ wid + v * x * 1.0/ hei);
rv += cos(xv) * m(x, y, 0);
vv += -sin(xv) * m(x, y, 0);
}
}
dftm(v, u, 0) = rv;
dftm(v, u, 1) = vv;
}
}
return dftm;
}
经过DCT的图像的频域的值不在[0,255]先要autoscale得到下图:

依然不方便观察需要将四个顶点的值向中心移动:

3.2 IDCT
逆变换同理:
template<class T>
static Matrix<T> idft(const Matrix<double> &m){
GASSERT(m.channels() == 2, "the matrix channle must be 2");
std::size_t hei = m.rows(), wid = m.cols();
Matrix<double> dftm(m.cols(), m.rows(), 1);
double mn = 1.0 / (hei * wid);
for(std::size_t y = 0; y < hei; y ++){
for(std::size_t x = 0; x < wid; x ++) {
double rval = 0.0, ival = 0.0;
for(std::size_t v = 0; v < hei; v ++){
for(std::size_t u = 0; u < wid; u ++) {
double vv = 2 * M_PI * (u * x * 1.0/ wid + v * y * 1.0 / hei);
double r = m(u, v, 0);
double i = m(u, v, 1);
rval += r * cos(vv) - i * sin(vv);
ival += i * cos(vv) + r * sin(vv);
}
}
double vv = sqrt(rval * rval + ival * ival) * mn;
dftm(x, y, 0) = vv;
}
}
return dftm.as<T>();
}
IDCT得到的图像: