LeetCode 84.柱状图中最大的矩形

题目链接：力扣（LeetCode）官网 - 全球极客挚爱的技术成长平台

题目描述：给定 n 个非负整数，用来表示柱状图中各个柱子的高度。每个柱子彼此相邻，且宽度为 1 。

求在该柱状图中，能够勾勒出来的矩形的最大面积。

解题思路

这题我们就是以每个柱子为基准，找到左边第一个比它矮的柱子left，右边第一个比它矮的柱子right，由于左右都比它矮，所以算矩形的时候肯定不能带上左右的柱子，中间的宽度也就是right - left - 1.这样就得到了宽度，我们再取以当前柱子为基准的高度，相乘再取result的最大值即可。

本题有几个需要注意的细节，首先我们找左右小于当前柱子高度的柱子的时候，我们应该用单调递减的栈来操作，找大于当前柱子的时候才用递增栈操作。

其次我们应该在原本柱子的首尾填上两个0，为什么呢？我们来看如下两种情况。

• 情况一：

当前我们已经遍历完了所以的柱子，确一次都没有操作，原因就是这个柱子的高度本身就是单调递增的，进栈之后变成单减的。找不到右边比其小的柱子，所以无法操作。而我们在其右边也就是结尾处加一个0，就可以正常操作了。

• 情况二：

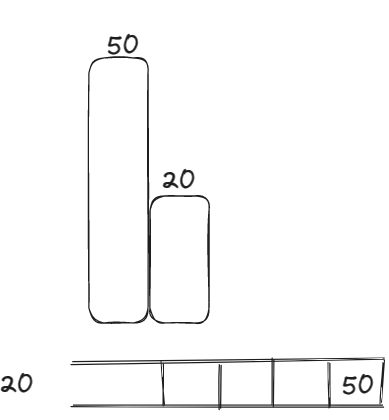
当前我们遍历到20的时候找不到左边比其小的柱子，就不会进行正常的操作，也就是不会取50这个柱子单独的面积，所以我们应该在开头也加上一个0，以保证正常操作。

// 版本二
class Solution {
public:
    int largestRectangleArea(vector<int>& heights) {
        stack<int> st;
        heights.insert(heights.begin(), 0); // 数组头部加入元素0
        heights.push_back(0); // 数组尾部加入元素0
        st.push(0);
        int result = 0;
        for (int i = 1; i < heights.size(); i++) {
            while (heights[i] < heights[st.top()]) {
                int mid = st.top();
                st.pop();
                int w = i - st.top() - 1;
                int h = heights[mid];
                result = max(result, w * h);
            }
            st.push(i);
        }
        return result;
    }
};

总结：

• 单调栈的应用，需要多想想为什么这里能用到单调栈。并且是想想用单增栈还是单减栈。