📙作者简介: 清水加冰,目前大二在读,正在学习C/C++、Python、操作系统、数据库等。
📘相关专栏:C语言初阶、C语言进阶、C语言刷题训练营、数据结构刷题训练营、有感兴趣的可以看一看。
欢迎点赞 👍 收藏 ⭐留言 📝 如有错误还望各路大佬指正!
✨每一次努力都是一种收获,每一次坚持都是一种成长✨

目录
前言
1. 堆
1.1 什么是堆
1.2 堆的性质
2. 堆的实现
2.1 堆的向下调整
2.2 堆的向上调整
2.3 堆的创建
2.3.1 定义堆
2.3.2 初始化和销毁
2.3.3 入堆
2.4 出堆
2.5 堆顶元素、判空、堆的数据个数
总结
前言
我们常见的二叉树有顺序存储和链式存储,顺序存储就是使用数组来存储二叉树,除了顺序存储,堆存储也是一种常见的选择。堆存储是一种基于数组的存储方式,它使用数组来表示堆的结构。在堆存储中,我们可以使用简单的数学公式来计算节点在数组中的索引,从而实现高效的访问和操作。
1. 堆
1.1 什么是堆
堆是一种特殊的二叉树,使用堆存储的二叉树都是完全二叉树,堆又可分为大堆和小堆。
大堆:大堆的子节点不得大于父节点。
小堆:小堆的子节点不得小于父节点。
可见文章:二叉树的存储结构
1.2 堆的性质
堆具有以下两个重要的性质:堆是一个完全二叉树,且堆中的每个节点的值都大于或等于(或小于或等于)其子节点的值,这被称为堆的堆序性质。
2. 堆的实现
2.1 堆的向下调整
我们知道,堆是使用数组存储的,那任何一个数组都可以是堆吗?当然不是,对具有两个重要的性质,要想构成堆,就需要对数组的数据进行调整。调整后,逻辑上就是一颗完全二叉树。向下调整算法有一个前提:左右子树必须是一个堆,才能调整。
如下图:
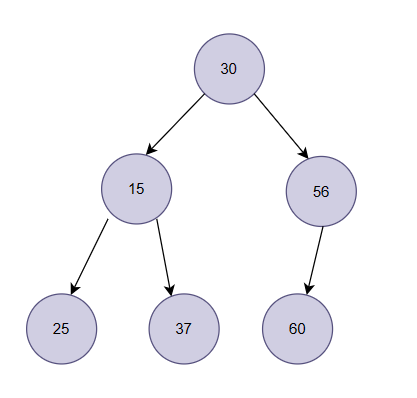
在逻辑上是一个完全二叉树,根节点的值是30,根节点的左右子树都是小堆,为了使整颗二叉树形成堆,就需要对数据进行调整。(小堆的子节点不得小于它的父节点)
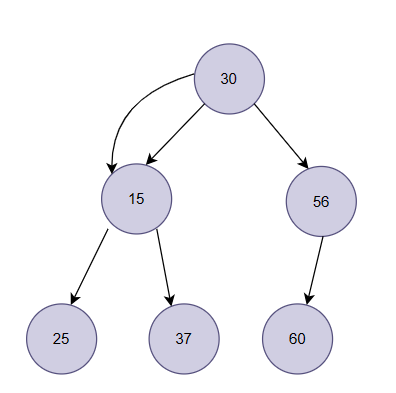
30比15大,就向下进行调整,15与30位置交换:
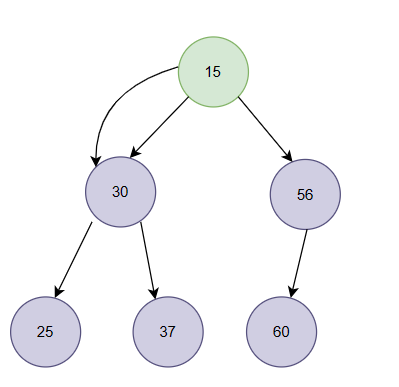
以此类推,进行调整:
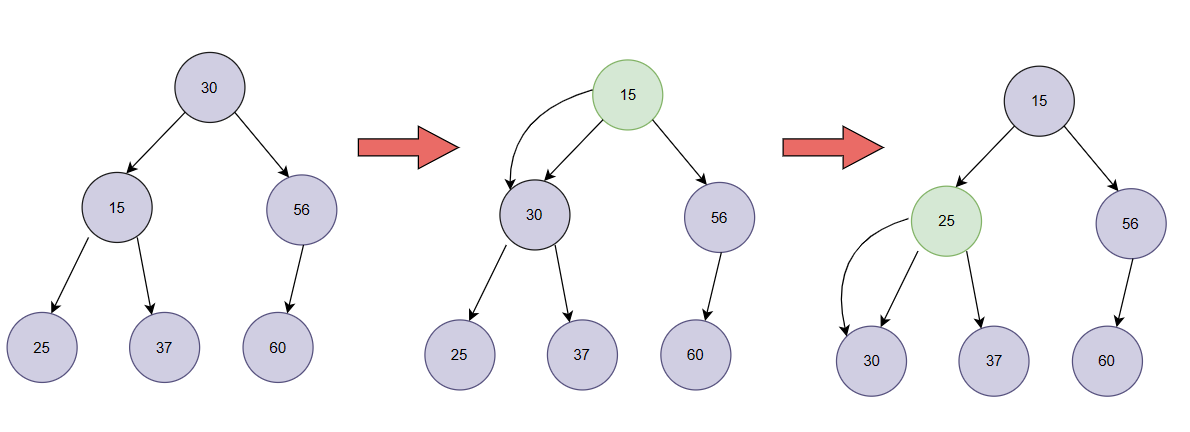
最终,被调整为一个小堆。(也可以调整为大堆)。
根据上述的逻辑,我们对向小调整的代码进行实现:
void HeapAdjustDown(HeapDatatype* data,int n,int parent)
{
int child = parent * 2 + 1;
while (child<n) //这里不能child+1<n
{
if (child+1<n && data[child + 1] < data[child])//改大堆两个if的符号都要改
{
child++;
}
if(data[child]<data[parent])
{
swap(&data[parent], &data[child]);//后续需要多次进行调用交换函数,就封装成一个函数
parent = child;
child = parent * 2 + 1;
}
else
{
break;
}
}
}传入一个堆、节点个数和父节点,通过父节点与孩子节点进行比较,找到较小的孩子,然后进行交换。n可以用于判断结束。注意:这里存在比较坑的点,这里我们使用了child+1,就需要判断child+1是否会越界的问题。
那为什么不在while循环处判断?
如果在while处判断就会产生新的bug,上述的例子无法展现,我们假设上述的二叉树,需要把30调整到60的位置,那30就会先和56进行交换,然后把child赋值给parent,child=child*2+1,赋值后,child就变成60这个节点,child+1就是空,那最后一次交换就不会执行。

2.2 堆的向上调整
堆可以向下调整,那也可以进行向上调整,向上调整和向下调整十分的相似,也是进行比较然后交换。向上调整也更为简单一些。流程如下:
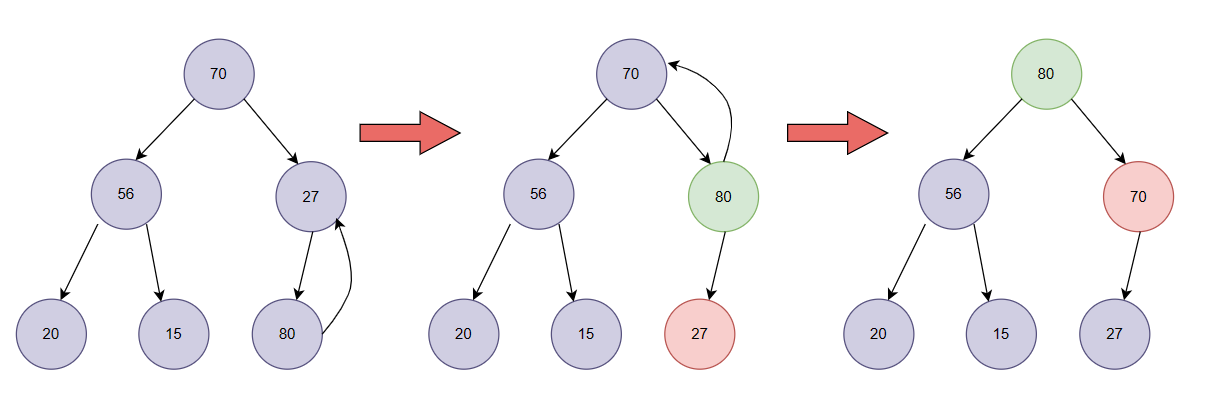
假设传入的子节点是80,80和父节点进行比较,80大进行交换,然后再和父节点比较,80仍然较大,再进行交换,直到形成一个堆结束。(此处为大堆),向下调整我们写的是调整小堆,这里我们向上调整也调整为小堆。代码如下:
void HeapAdjustUP(HeapDatatype* data, int child) {
int parent = (child - 1) / 2;
while (child > 0)
{
if (data[child] < data[parent]) //回调函数qsort的compare函数
{
swap(&data[child], &data[parent]);
child = parent;
parent = (parent - 1) / 2;
}
else
{
break;
}
}
}写代码时要注意:判断循环结束的条件,这里为什么不用parent>0进行判断?如果最后需要对整棵树的根节点进行交换,parent是可以等于0的,而child等于0时,即最终树的根节点交换完毕,如果再-1除2,还是0.所以拿child>0作为判断条件即可,如果没有交换到根节点,就已经构成了堆,那就break跳出循环即可。
2.3 堆的创建
注意上述堆的调整我们传入的参数,并不是创建的Heap(堆),而是以数组的形式传入,这样我们就可以直接调用这两个函数接口进行建堆。
for (int i = ; i < ; i++)
{
AdjustUp(arr, i);
}只需这样就可以构建一个堆。这里我们就不进行细说,后续的堆排序会进行介绍。这里我们用老常规的方法,创建一个顺序表,然后进行建堆。
2.3.1 定义堆
顺序表的定义就非常常规了,和之前一样:
typedef int HeapDatatype;
typedef struct Heap {
HeapDatatype* data;
int size;
int capacity;
}HP;2.3.2 初始化和销毁
初始化
void InitHeap(HP* php) {
assert(php);
php->data = NULL;
php->size = 0;
php->capacity = 0;
}销毁
void DestoryHeap(HP* php) {
assert(php);
free(php->data);
php->data = NULL;
php->capacity = php->size = 0;
}初始化和销毁都很常规,和顺序表一致。
2.3.3 入堆
把数据入堆,先把数据入到顺序表中,然后进行调整。我们可以调用向上调整或者向下调整,只是传入的参数不同。
代码如下:
void PushHeap(HP* php, HeapDatatype data) {
assert(php);
if (php->capacity == php->size)
{
int newcapacity = php->capacity == 0 ? 4 : php->capacity * 2;
HeapDatatype* tmp = (HeapDatatype*)realloc(php->data, sizeof(HeapDatatype) * newcapacity);
if (tmp == NULL)
{
perror("realloc fail");
exit(-1);
}
php->data = tmp;
php->capacity = newcapacity;
}
php->data[php->size++] = data;
HeapAdjustUP(php->data, php->size - 1);
}使用循环调用入堆接口,就可以完成堆的创建。
2.4 出堆
出堆,我们可以来思考一下,出堆是单纯的将数组最后一个数据删除掉吗?当然不是,如果只是单纯的删除最后的数据,那和顺序表又有什么区别,这样做是没有意义的。
堆在数组中的第一个元素一定是这个数组中的最值(最大或最小值),所有我们出堆,删除的是数组中的第一个元素,也就是二叉树的根。那我们要怎么去删除呢?直接删除二叉树的根?
如下图:
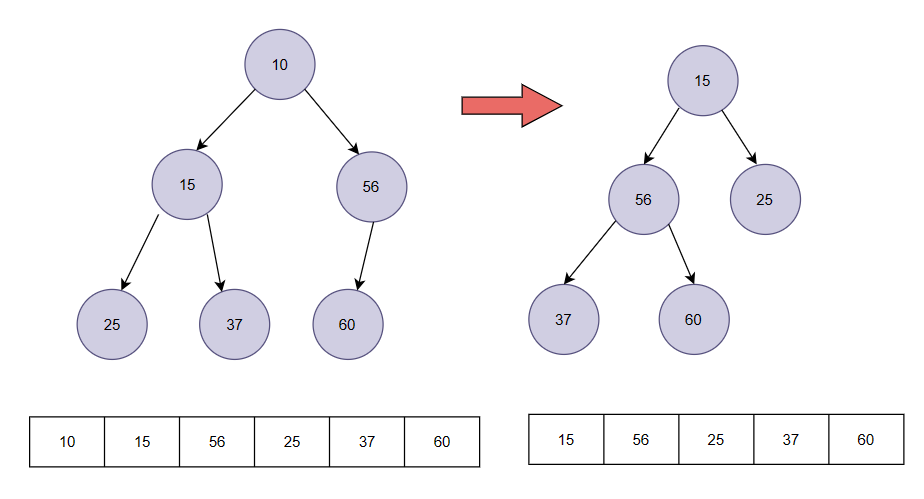
如果直接删除二叉树的根节点,剩下的部分产生的结构就会发生变化,变化后的二叉树还是堆吗?所以说直接删除的方法是不可行的。那要如何删除呢?
我们可以这样搞:可以先把数组的第一个元素和最后一个元素进行交换,然后删除最后一个元素,最后再进行调整。这样就既可以删除根节点,而又不打乱堆的结构。
根据这个逻辑,代码实现如下:
void PopHeap(HP* php)
{
assert(php);
assert(php->size > 0);
swap(&php->data[0], &php->data[php->size - 1]);
php->size--;
HeapAdjustDown(php->data,php->size,0);
}注意这里只能使用向下调整。
2.5 堆顶元素、判空、堆的数据个数
剩余部分就非常简单了
//堆顶元素
HeapDatatype HeapTop(HP* php)
{
assert(php);
assert(php->size > 0);
return php->data[0];
}
//判空
bool HeapEmpty(HP* php)
{
assert(php);
return php->size == 0;
}
//堆的数据个数
int HeapSize(HP* php) {
assert(php);
return php->size;
}最后我们可以来测试一下,我的测试代码如下:
int main()
{
HP hp;
int arr[6] = { 70,65,100,32,50,60 };
InitHeap(&hp);
for (int i = 0; i < 6; i++)
{
PushHeap(&hp, arr[i]);
}
HeapPrint(&hp);
printf("堆的数据个数:%d\n", HeapSize(&hp));
while (!HeapEmpty(&hp))
{
printf("%d ", HeapTop(&hp));
PopHeap(&hp);
}
DestoryHeap(&hp);
}总结
无论是学习数据结构还是应用数据结构,了解和理解堆存储都是非常有价值的。希望本篇博客能够为大家提供有价值的知识和见解,帮助大家更好地理解堆。最后,感谢阅读!