目录

💥1 概述

📚2 运行结果

🎉3 参考文献

👨‍💻4 Matlab代码

---

💥1 概述

时间序列预测方法是科学、经济、工程等领域的研究重点之一。经典的时间序列预测方法在用于非线性系统预测时有一定的困难,而神经网络具有较好的非线性特性,为时间序列预测开辟了新的途径。但神经网络具有易陷入局部极小值以及全局搜索能力弱等缺点;而遗传算法具有较好的全局最优搜索能力,遗传神经网络将两者结合,既保留了遗传算法的全局寻优的特点,又兼有神经网络的非线性特性和收敛的快速性。Mackey-Glass(MG)混沌时间序列具有非线性特性,是时间序列预测问题中的基准问题之一,具有代表性。

时滞混沌系统即具有混沌运动的时滞系统。时滞系统是系统中一处或几处的信号传递有时间延迟的系统。所谓混沌是指具有以下特点的一类现象：由确定性产生；具有有界性；具有非周期性；初始条件具有极端敏感性。

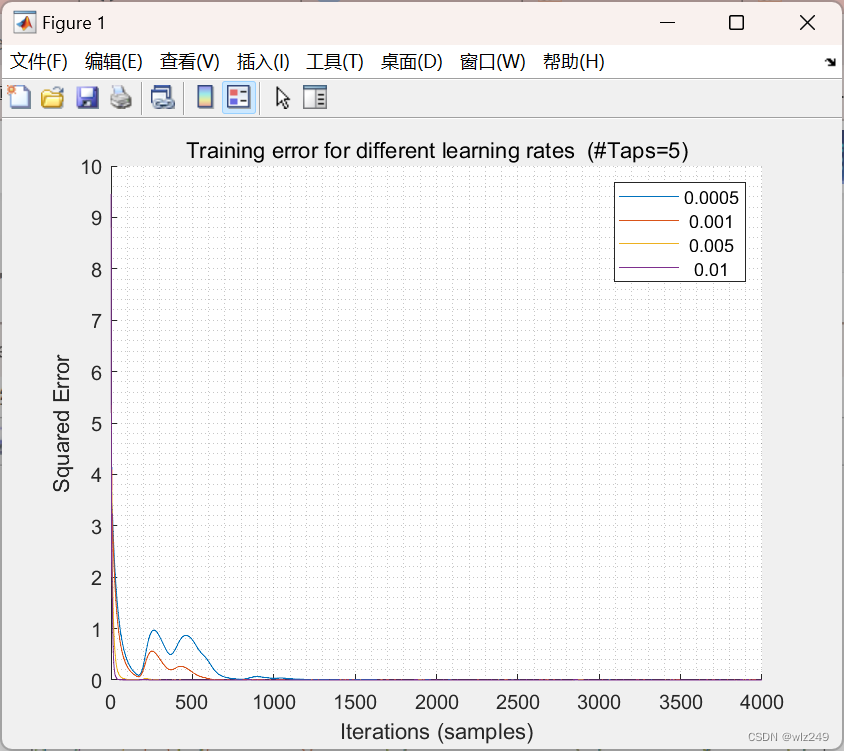
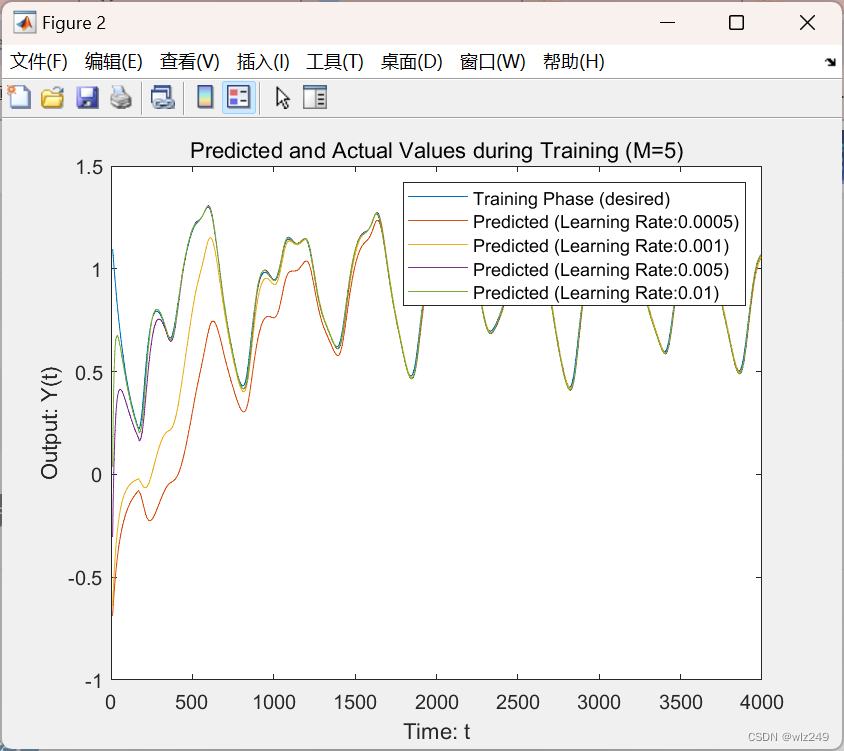
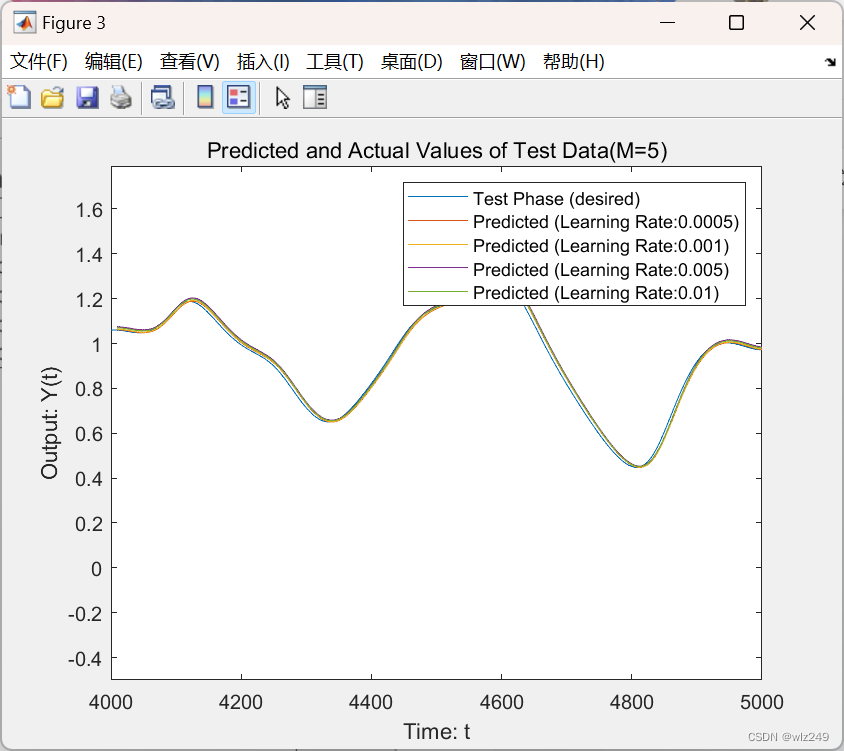
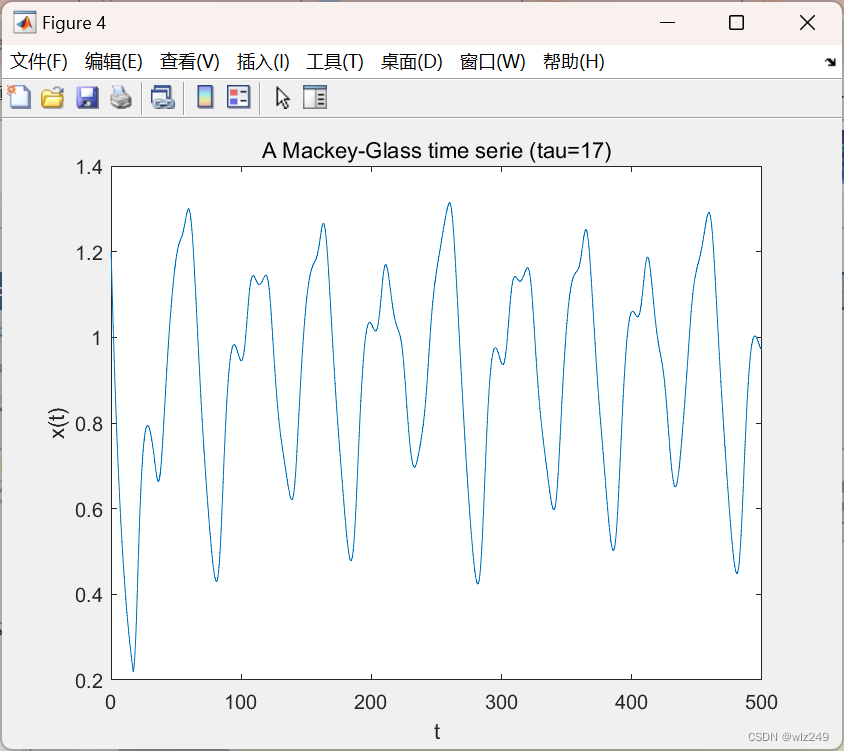
📚2 运行结果

 

 

🎉3 参考文献

[1]邵海见,邓星.基于RBF神经网络结构选择方法的Mackey-Glass与Lorenz混沌时间序列预测建模[J].江苏科技大学学报(自然科学版),2018,32(05):701-706.

👨‍💻4 Matlab代码

%% mackeyglass
% This script generates a Mackey-Glass time series using the 4th order
% Runge-Kutta method.

%% Input parameters
a        = 0.2;     % value for a in eq (1)
b        = 0.1;     % value for b in eq (1)
tau      = 17;		% delay constant in eq (1)
x0       = 1.2;		% initial condition: x(t=0)=x0
deltat   = 0.1;	    % time step size (which coincides with the integration step)
sample_n = 5000;	% total no. of samples, excluding the given initial condition
interval = 1;	    % output is printed at every 'interval' time steps


%% Main algorithm
% * x_t             : x at instant t         , i.e. x(t)        (current value of x)
% * x_t_minus_tau   : x at instant (t-tau)   , i.e. x(t-tau)   
% * x_t_plus_deltat : x at instant (t+deltat), i.e. x(t+deltat) (next value of x)
% * X               : the (sample_n+1)-dimensional vector containing x0 plus all other computed values of x
% * T               : the (sample_n+1)-dimensional vector containing time samples
% * x_history       : a circular vector storing all computed samples within x(t-tau) and x(t)

time = 0;
index = 1;
history_length = floor(tau/deltat);
x_history = zeros(history_length, 1); % here we assume x(t)=0 for -tau <= t < 0
x_t = x0;

X = zeros(sample_n, 1); % vector of all generated x samples
T = zeros(sample_n, 1); % vector of time samples

for i = 1:sample_n
    X(i) = x_t;
    if tau == 0
        x_t_minus_tau = 0.0;
    else
        x_t_minus_tau = x_history(index);
    end

    x_t_plus_deltat = mackeyglass_rk4(x_t, x_t_minus_tau, deltat, a, b);

    if (tau ~= 0)
        x_history(index) = x_t_plus_deltat;
        index = mod(index, history_length)+1;
    end
    time = time + deltat;
    T(i) = time;
    x_t = x_t_plus_deltat;
end

% Save training and test data
Data = X;
save('Dataset\Data.mat','');

figure
plot(T, X);
set(gca,'xlim',[0, T(end)]);
xlabel('t');
ylabel('x(t)');
title(sprintf('A Mackey-Glass time serie (tau=%d)', tau));

主函数部分代码：

clc
clear all
close all

%% Load Mackey Glass Time series data
load Dataset\Data.mat 

%% Training and Testing datasets
% For training
Tr=1:4000;    % First 4000 samples for training
Xr(Tr)=Data(Tr);      % Selecting a chuck of series data x(t)
% For testing
Ts=4000:5000;   % Last 1000 samples for testing
Xs(Ts)=Data(Ts);      % Selecting a chuck of series data x(t)

%% LMS Parameters
% We run the LMS algorithm for different learning rates
etaValues = [5e-4 1e-3 5e-3 0.01]; % Learning rate
M=5;    % Order of LMS filter
W_init=randn(M+1,1); % Initialize weights

figure(2)
plot(Tr(2*M:end-M),Xr(Tr(2*M:end-M)));      % Actual values of mackey glass series

figure(3)
plot(Ts,Xs(Ts));        % Actual unseen data

for eta = etaValues
      
    U=zeros(1,M+1); % Initialize values of taps
    W=W_init; % Initialize weights
    E=[];         % Initialize squared error vector
    
    %% Learning weights of LMS (Training)
    for i=Tr(1):Tr(end)-1
        U(1:end-1)=U(2:end);    % Shifting of tap window
        U(end)=Xr(i);           % Input (past/current samples)
        
        Y(i)=W'*U';             % Predicted output
        e(i)=Xr(i+1)-Y(i);        % Error in predicted output

        W=W+eta*e(i)*U';     % Weight update rule of LMS

        E(i)=e(i).^2;   % Concatenate current squared error
    end

    %% Prediction of a next outcome of series using previous samples (Testing)
    for i=Ts(1):Ts(end)
        U(1:end-1)=U(2:end);    % Shifting of tap window
        U(end)=Xs(i);           % Input (past/current samples)

        Y(i)=W'*U';             % Calculating output (future value)
        e(i)=Xs(i)-Y(i);        % Error in predicted output

        E(i)=e(i).^2;   % Current mean squared error (MSE)
    end
    
    % Plot the squared error over the training sample iterations
    figure(1),hold on;
    plot(Tr(1:end-1),E(:,Tr(1:end-1)));   % MSE curve
    hold off;
    
    % Plot the predicted training data
    figure(2), hold on;
    plot(Tr(2*M:end-M),Y(Tr(2*M:end-M))')   % Predicted values during training
    hold off;

%   Comment out the following parts to plot prediction of the test data    
    figure(3), hold on; 
    plot(Ts(2*M:end),Y(Ts(2*M:end))');  % Predicted values of mackey glass series (testing)
    hold off;
    
    MSEtr= mean(E(Tr));  % MSE of training
    MSEts= mean(E(Ts));  % MSE of testing

    disp(['MSE for test samples (Learning Rate: ' num2str(eta) '):' num2str(MSEts)]);
    
end