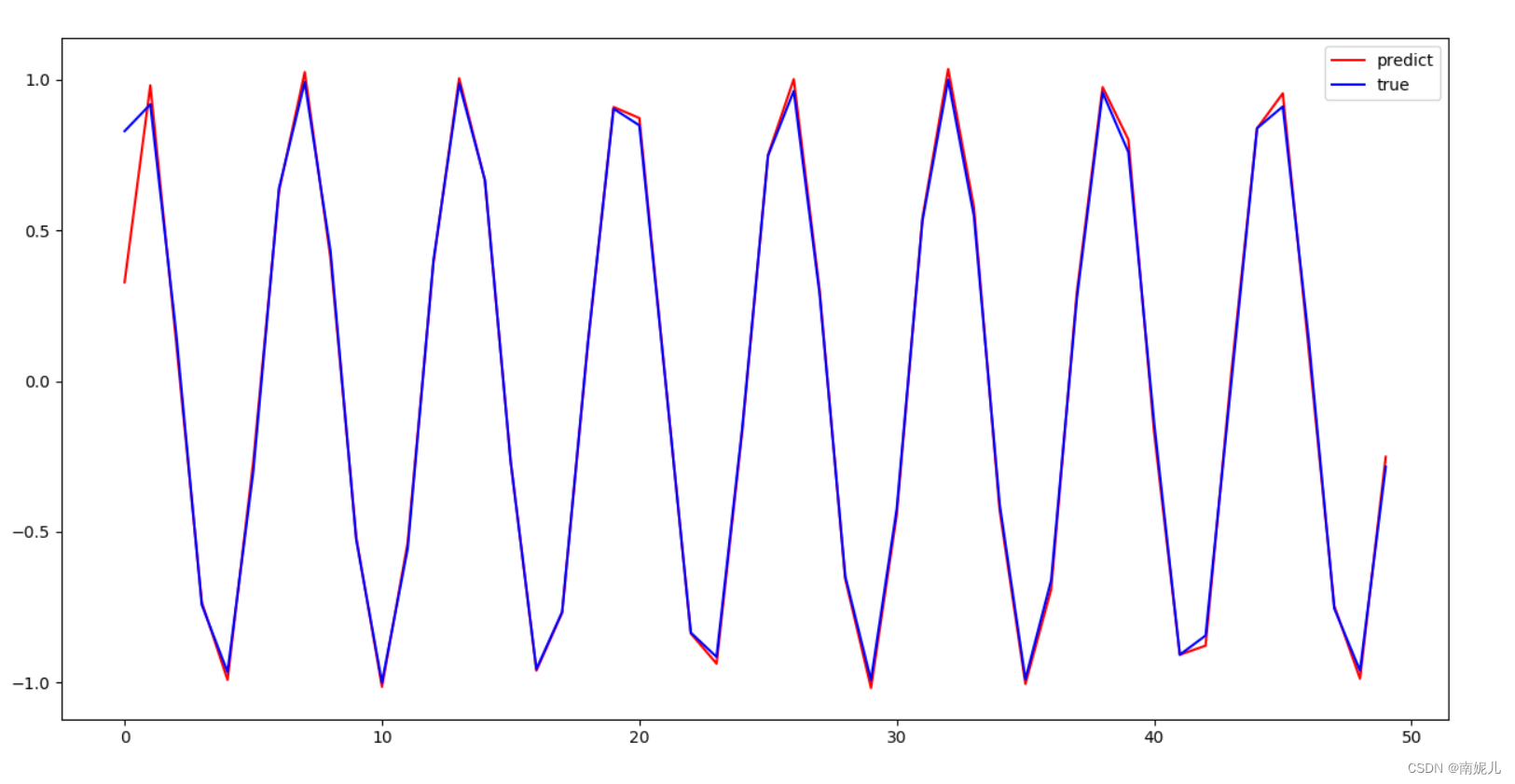
0.摘要
卷积神经网络( CNNs )在二维计算机视觉领域取得了巨大的突破。然而,其不规则的结构使得直接在网格上利用卷积神经网络的潜力变得困难。细分曲面提供了层次化的多分辨率结构,其中一个封闭的二维流形三角网格中的每个面恰好与三个面相邻。受这两点启发,本文提出了SubdivNet,这是一个具有创新性和通用性的用于具有Loop细分序列连通性的三维三角网格的CNN框架。将二维图像中的网格面和像素进行类比,我们可以提出一个网格卷积算子来聚合来自附近面的局部特征。通过利用面邻域,该卷积可以支持标准的2D卷积网络概念,例如可变的核大小、步幅和膨胀。基于多分辨率层次结构,我们利用池化层将四个面统一合并为一个,以及上采样方法将一个面分割为四个。因此,许多流行的2D CNN架构可以很容易地适应处理3D网格。具有任意连通性的网格可以通过自参数化重新网格化为具有循环细分序列连通性,使得SubdivNet成为通用方法。广泛的评估和各种应用表明了SubdivNet的有效性和高效性。
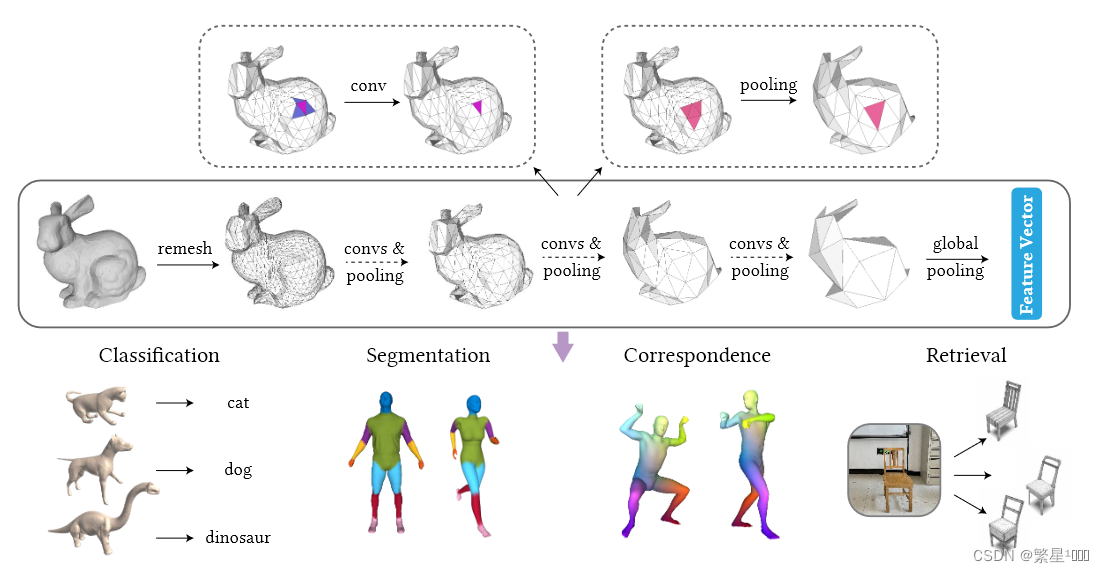
1. Introduction
- 深度卷积网络在2D CV中取得了巨大的成功——》泛化到三维几何处理,PointNet是点云处理的开创性方法——》3维几何处理已经被扩展到其他3D数据形式:体素、网格。
- 本文,研究使用网格表示的3维几何学习——》介绍网格的优势: 多边形网格是最常见的三维数据表示形式之一,在建模、渲染、动画、3D打印等领域有着广泛的应用。网格比点云多包含拓扑信息。多边形网格比体素能更有效地表示几何上下文,因为它们只描述物体的边界,省略了内部多余的元素。
- 2D CNNs在图像域成功的基础是其固有的规则网格结构允许分层的图像金字塔,这使得CNNs能够通过下采样和上采样来探索不同大小的特征。——》介绍CNN运用到网格的两个主要障碍: (1)任意网格是不规则的,缺乏图像中像素的网格化排列,难以定义具有可变核大小、步长和膨胀的标准卷积。这使得3D几何学习方法无法利用图像领域成熟的网络架构。(2)顶点之间和面之间的非结构化连通性使得网格无法找到简单的由细到粗的结构。可以通过网格简化来考虑细节层次( LOD ),但是每个层次之间的几何基元的映射没有很好的定义,并且不能从LOD层次结构中得到直观的池化算子。
- 为了将卷积神经网络的强大功能应用于网格,人们努力在表面上定义特殊的卷积操作。——》简单介绍现有的方法: (1)这类方法通常试图将顶点的邻域编码或重采样到一个规则的局部域中,其中卷积操作可以派生出来。(2)最近,网格降采样方案被提出来使用边折叠来动态合并区域,但它们并不能像在2D池化中那样保证处处均匀扩大的感受野。(3)尽管注意力机制可以通过将网格视为图来捕获全局上下文,但这样做的计算开销很大。
- 介绍本文的主要灵感启发: 相反,受2D CNNs中允许将局部特征聚合为不同级别的更大规模特征的图像金字塔的启发,(1)我们注意到细分曲面也构建了定义良好的层次网格金字塔。细分曲面是由粗网格细化产生的光滑曲面。特别地,在Loop细分[ Loop 1987 ]中,每个三角形网格面被分割成4个三角形,然后更新顶点位置以平滑新的网格。因此,Loop细分方案给出了从粗网格到细网格的1到4的面映射。(2)相应地,如果一个网格与Loop细分曲面具有相同的连通性,那么它与一个一级粗的网格具有天然的对应关系,并且一个精心构造的Loop细分曲面可以在几个层次上保持Loop性质,从而形成一个由细到粗的层次结构。(3)此外,任意闭合二维流形网格中的每个面恰好被另外3个面包围。固定数量的面邻居具有类似于图像中像素的规则结构,使其适用于推导网格上的标准卷积操作。
- 简要介绍本文的主要工作: 在本文中,我们提出了SubdivNet,它可以学习具有Loop细分序列连通性的网格的特征表示。利用面的近邻,我们在网格面上定义了一个新的卷积,它支持可变的核大小、步幅和膨胀。因此,我们可以在一个大的感受野上操作。由于我们的新卷积在三角形网格上的灵活性,在图像域成功的神经网络,如VGG,ResNet,DeepLabv3 +,可以自然地适应网格。
- 解释本文可能的限制以及解决办法: SubdivNet需要一个细分序列连通性的网格作为输入,可能会出现过度限制。然而,任何表示任意的闭二维流形的三角网格都可以通过自参数化来重新划分网格使其具有这一性质。因此,SubdivNet可以作为任意封闭二维流形三角网格的通用特征提取器。
- 介绍本文工作的性能: SubdivNet在三维形状分析方面取得了最先进的性能,例如网格分类、分割和形状对应。消融研究验证了所提出的卷积、基于细分的池化和先进网络架构的有效性。
主要贡献
- 一个通用的网格卷积操作,允许类似于标准2D卷积的可变内核大小、步幅和膨胀,使众所周知的2D CNN适应网格任务成为可能。
- SubdivNet,一种基于网格卷积和细分序列连通性的通用网格神经网络架构,具有统一的池化和上采样,用于几何深度学习,支持密集预测任务,
- 表明SubdivNet为形状对应和形状检索等各种应用提供了优异的结果。
2. Related work
2.1 3D几何学习
- 将三维形状转化为图像 ,如无序的投影集[ Su等2015]、全景图[ Shi等2015]或几何图像[ Sinha等2016],然后在其上运行2D CNN。这类间接方法是姿态敏感的,因为它涉及到一个额外的依赖于视图的投影步骤。
- 体数据: 另一种直接的解决方案是在其固有的三维空间中表示形状,如体数据,使用3D CNN或适应更高分辨率的。
- 点: 最近,由于三维传感器获取点云数据的便利性,基于点的学习技术出现了。
- 网格: 然而,体数据的高计算需求和点云拓扑信息的缺失使得现有的管线效率低下。然而,在网格曲面上学习的方法克服了上述问题并显示出潜力。
2.2 面向网格的深度学习
2.2.1 基于点
- 一些工作通过将采样点的邻域局部编码到规则域来对3D形状进行深度学习,其中卷积操作(或核函数)可以模仿图像的卷积操作。
- 另外一系列工作直接在网格结构上应用卷积。
- 一些方法[ Chen et al 2020 ; Dai and Nießner 2019 ;科斯特里科夫et al 2018 ; Monti et al 2017]使用图神经网络( GNN )来使用顶点连通性。
- Pixel2Mesh [ Wang等2018]通过细分从粗到细生成网格,并通过GNN更新几何。
- Lim等[ 2018 ]和Gong等[ 2019 ]提出了顶点k -环邻域内的螺旋卷积模式。
- DiffusionNet [ Sharp等2021]和HodgeNet [斯米尔诺夫和所罗门2021]扩展了拉普拉斯算子来学习曲面表示。
- 虽然这些方法可以学习局部表示,但它们通常不能学习网格中的多尺度和上下文信息。
- 与我们的方法更接近的是具有层次设计的方法。
- 在谱域可以采用膨胀核参数化[ Yi等2017],以及网格降采样和上采样[ Ranjan等2018],定义网格卷积来聚合多尺度信息。
- Schult等人[ 2020 ]根据测地距离和欧氏距离将两种分别定义在邻域上的卷积结合起来,并利用网格简化提供多分辨率架构。
- 基于细分序列连通性,我们的方法提供了一种更通用和标准的直接定义在网格上的卷积;因此,它支持可变的内核大小、步幅和伸缩。
2.2.2 基于边
- 二维流形三角网格中的每条边都与两个面和四个"下一个"边相邻。
- MeshCNN [ Hanocka等2019]利用该特性定义了一个排序不变卷积。
- PD-MeshNet [ Milano et al 2020]从输入网格中构建一个原始图和一个对偶图,然后使用图注意力网络[ Monti等2018 ; Velickovic等2018]对这些图进行卷积。
- Mesh Walker [拉哈夫和塔尔2020]通过沿边缘行走而不是利用邻域结构来提取形状特征。
- MeshCNN和PD - MeshNet通过动态收缩边来简化网络内部的网格,Mesh Walker通过变步长行走构建层次化结构。
- 与我们的方法不同,他们没有提供一个均匀扩大感受野的下采样方案,这是2D CNNs中的一个成功策略。
2.2.3 基于面
- 基于面的方法关注如何高效、有效地从相邻面中采集信息。
- Xu等[ 2017 ]提出了一种考虑k环邻域的旋转不变面方法,用于定义网格上的卷积;它由面曲率引导。
- 由Lian等[ 2019 ]提出的MeshSNet采用图约束的网格单元节点来集成局部到全局的几何特征。
- MeshNet [ Feng等2019]通过两个网格卷积层聚合其1环邻域来学习面的空间和结构特征。
- DNF-Net [ Li等2020]使用多尺度嵌入和残差学习策略对裁剪局部块上的网格法线进行去噪。
- Hertz等[ 2020 ]使用类似Pixel2Mesh [ Wang等2018]的3 - face卷积和基于细分的上采样生成几何纹理。
- SubdivNet采用规则均匀的下采样方案,建立由细到粗的网格层次结构。我们的卷积还利用了面的远邻居,因此可以有更大的感受野。与Xu et al . [ 2017 ]相比,我们的卷积有效地支持了跨步和大膨胀,使我们能够更好地捕获长程特征。
2.3 细分曲面与多分辨率建模
2.3.1 细分曲面
- 细分曲面是由粗网格细化产生的光滑曲面。
- 最著名的网格细分算法
- 针对四边形网格的Catmull - Clark细分
- 针对三角形网格的Loop细分。它们插入新的顶点和边,分割面,线性更新顶点位置。
- 其他细分方案
- 最著名的网格细分算法
2.3.2 多分辨率建模
- 多分辨率建模又称细节层次建模,旨在构建由细到粗的网格序列,广泛应用于网格压缩、编辑和快速绘制。
- 关于这个主题已经有很多工作,我们将只考虑从细到粗保持细分序列连通性的方法:我们需要一个整体层次的网格都具有Loop细分连通性。
- MAPS [ Lee等1998]是一个开创性的工作,它计算网格在简化版本的网格上的参数化。然后,在简化后的网格表面构造一个具有剖分序列连通性的新网格。最后,通过参数化将新网格的顶点投影回输入面。
- 该思想通过[ Guskov等, 2002,2000 ;霍达科夫斯基等, 2003 ; Kobband等1999]在失真度和平滑度方面进一步改进。
- Liu等[ 2020 ]也对MAPS算法进行了扩展,用于生成用于网络训练的多分辨率网格。
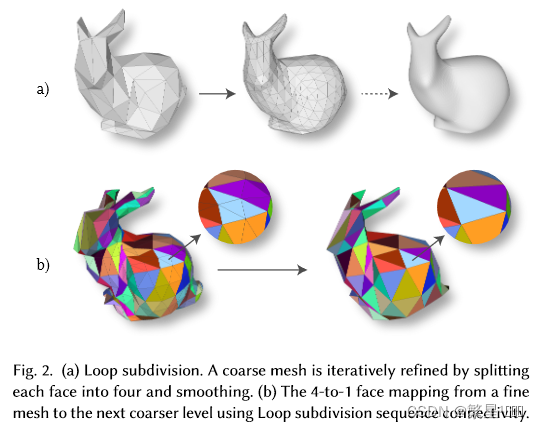
- 关于这个主题已经有很多工作,我们将只考虑从细到粗保持细分序列连通性的方法:我们需要一个整体层次的网格都具有Loop细分连通性。
3.方法
3.1 卷积与卷积核
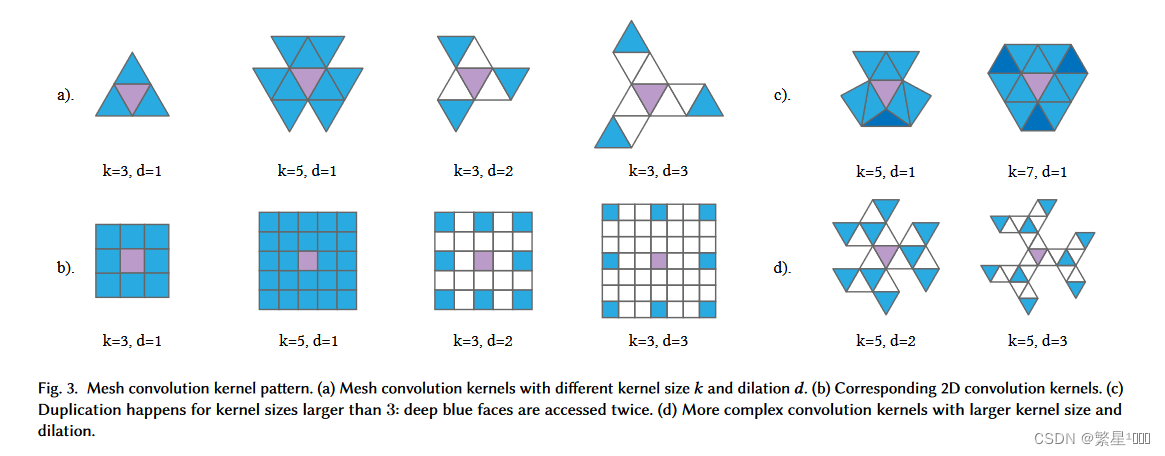
膨胀顺序:zig-zag
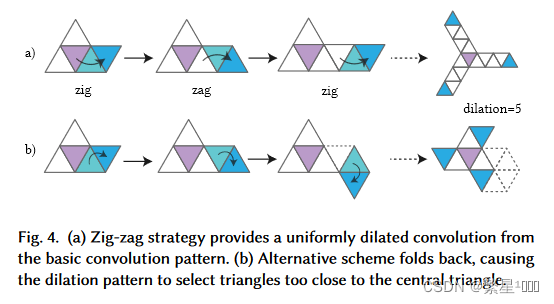
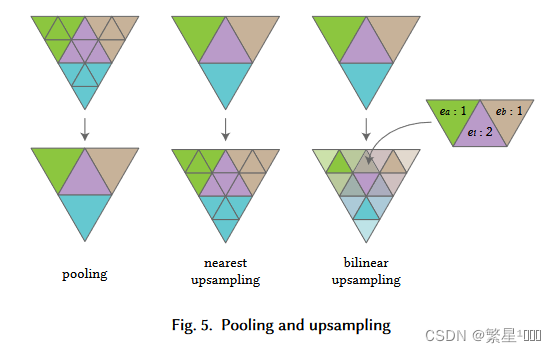
3.2 池化和反池化
- 池化算子
- 反池化算子
- 最近邻上采样
- 双线性上采样
3.3 向原始网格传播特征
对于原始网格中的每个面
f
R
f^R
fR,我们找到重划分网格中最近的面
f
0
r
f^r_0
f0r。设
f
i
r
f^r_i
fir ( i = 1,2,3)为
f
0
r
f^r_0
f0r的3个相邻面。然后通过插值得到
f
R
f^R
fR上的特征向量,通过距离加权:
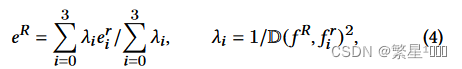
- 其中D ( · )是面中心之间的欧氏距离。
3.4网络结构
得益于所提出的卷积提供的规律性,我们可以很容易地将流行的2D卷积网络应用于3D网格。在我们的实验中,我们实现了:
- VGG风格的网络用于分类,
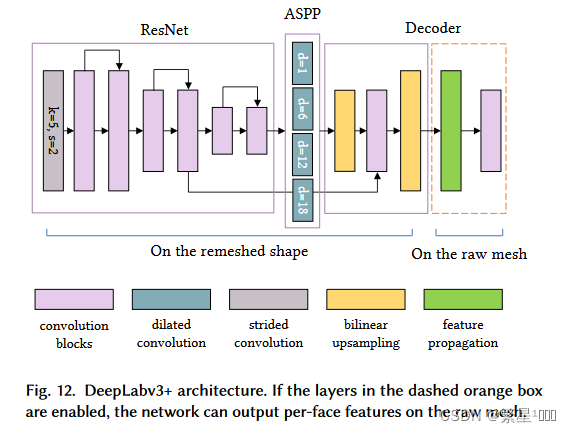
- 具有ResNet50网络主干的UNe和Deep Labv3 +用于密集预测。
- Deep Labv3 +为二维图像分割提供了最先进的性能;其核心思想是利用空洞卷积扩展感受野。这种机制对于3D网格也是有帮助的;
3.5 输入特征
4. Remeshing for Subdivision connectivity
- 对于全局形状比较重要且可以容忍局部扭曲的任务,如分类,我们选择MAPS算法来实现更高的全局特征聚合程度,
- 而对于局部细节比较关键的任务,如细粒度分割,我们采用Liu等人的方法和更大的基尺寸。
- 两种网格重划分算法都要求输入是流形和封闭的,否则局部参数化可能失败。更一般的网格必须事先转换为水密流形,通过额外的预处理(见附录C)。