一、前言
本文接续前篇教学 Pytorch 与线性回归 ,本文着重在 Activation Function ( 中文称 激励函数 ),我们会介绍激励函数 (也有人称 激活函数? 激发函数? ) 为什么会有用,还有通过示例来探讨/实作(本文介绍常用的 ReLU, Tanh, Sigmoid, Softmax )
阅读本文需要有矩阵计算的知识,还有知道线性回归的原理
另外我们也使用 Pytorch
本文希望透过生活中的范例,白话文的精神,让各位了解 Deep Learning/Machine Learning 中的激励函数 ( Activation Function )
了解激励函数,其实就是往 Deep Learning 更迈进了一步
二、激励函数(Activation Function) 为什么会有用
网络上大家应该看过什么激励函数解决线性,非线性问题,这些都是抽象的老生常谈,不是数学领域的人应该很难理解,但其实他的概念很简单:
我相信编程程序的人,一定都有用过if这个语法
而激励函数的精神,其实就是用数学的形式来表达if else语法
核心概念就是这么简单
我们通过大量的 if else 去编织(矩阵计算)出结果,这就是为什么需要激励函数,用这种方法配合微分就可以解决问题
三、激励函数 — 生活中的概念范例
我们来看一个简单的问题:传统电饭锅 / 电热水壶

電鍋示意圖,非當事電鍋
傳統電鍋/熱水壺是溫度達到一個程度後就會跳開 ( 燒開水 ),這就是激勵函數的概念
例如:
- 溫度 130 度 以下保持加熱 ( switch = 0 )
- 超過 130 度的時候跳停 (switch = 1 )

溫度在 130 度的時候跳停 ( switch 1 )
我們來看看程式怎麼寫
def check(t):
if t > 130:
return 1
return 0看到我們使用 if 來解決問題了嗎?
四、激勵函數之 Sigmoid
數學上,我們可以透過函數達到這種效果,我們來看 sigmoid 這個範例;關於 Sigmoid 的計算公式有興趣可以看看 wiki ,我們這邊主要說明他的概念為什麽有效
簡單的說,Sigmoid 是透過計算讓他的範圍維持在於 0 到 1 之間
先看 Pytorch 程式碼繪製的 sigmoid activation function
x = torch.arange(-10., 10., step=0.01)
plt.plot(x, torch.sigmoid(x))
解说:
- torch.arange 是产生一个 -10 ... 10 的 array ( tensor )
- torch.sigmoid 就是 torch 的 sigmoid 函数
- 我们把它绘制成图表来看
可以看到在不同的 X 范围,最多输出 ( y) 就是 0~1 之间,就算是 -100000 到 100000 也是 ( 如下图)

看起来是不是和电饭锅跳停的图片有八成像?
那么问题来了,怎么套用在我们的电饭锅问题上?
五、激励函数与线性回归组合
我们这边,假设 x 是温度,是不是只要有办法让 sigmoid(x) 在 x 大于 130的时候输出 1 就好 ?
回到线性归公式, y = ax + b
所以我们要改写成 y = sigmoid(ax + b)
(a 和 b 是我们的变量 )
我们写成 Pytorch 代码来看,套用之前文章讲到的自动微分
( 后面有完整可执行示例,以下是片段代码)
a = torch.rand(1, requires_grad=True)
b = torch.rand(1, requires_grad=True)
def forward(t):
return torch.sigmoid( a * t + b )- 这边我们要使用自动导数 (Auto grad ) 来找出正确的 a, b ,所以 requires_grad=True
- 我们这边 forward(t) 使用 t ,避免变量名称与 x 混淆
先看我们没有训练前的结果
# 溫度範圍 0 ~ 200 度
x = torch.arange(0, 200, step=0.1)
# y_p 是 y predict, 我們預測的 y
y_p = forward(x).detach().numpy() # .detach().numpy() 是轉換成 numpy
# 繪圖
plt.plot(x, y_p)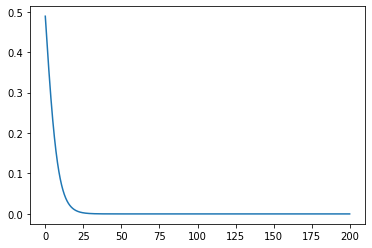
還沒訓練以前,看起來一點也不像是有用的東西
現在我們開始訓練,這之前,先準備一下正確答案 ( y 為正確答案)
def check(t):
if t > 130:
return 1
return 0
y = torch.tensor([check(t) for t in x]).float() 註 1: torch.tensor 是將 python array 變成 torch 的 array ( tensor ),類似於 np.array
註 2: 因為我們計算都是用 float, 所以要轉成 torch 的 float
然後準備一下 優化器 和 損失函數 ( Loss function )
( 優化器我們使用 Adam ,損失函數我們先用 BCELoss, 這部分有空再另寫文章介紹… )
# 準備變數
a = torch.rand(1, requires_grad=True)
b = torch.rand(1, requires_grad=True)
# 定義計算
def forward(t):
# y = sigmoid(ax + b)
return torch.sigmoid(a * t + b)
# 優化器
opt = torch.optim.Adam([a, b], lr=0.05)
# 損失函數
loss_func = torch.nn.BCELoss()開始訓練的程式碼
for _ in range(10000):
y_p = forward(x) # 預測 y
loss = loss_func(y_p, y) # 計算誤差
opt.zero_grad() # 導數重置
loss.backward() # 反向傳導
opt.step() # 優化器修正我們整理一下,完整可執行範例 :
import numpy as np
import torch
import matplotlib.pyplot as plt
# 溫度範圍
x = torch.arange(0, 200, step=0.1)
# 我們先做出正確答案
def check(t):
if t > 130:
return 1
return 0
y = torch.tensor([check(t) for t in x]).float()
plt.figure(figsize=(30, 10))
plt.subplot(1, 2, 1)
plt.plot(x, y)
# 準備變數
a = torch.rand(1, requires_grad=True)
b = torch.rand(1, requires_grad=True)
# 定義計算
def forward(t):
# y = sigmoid(ax + b)
return torch.sigmoid(a * t + b)
# 優化器
opt = torch.optim.Adam([a, b], lr=0.05)
# 損失函數
loss_func = torch.nn.BCELoss()
# 開始訓練
for _ in range(10000):
y_p = forward(x) # 預測 y
loss = loss_func(y_p, y) # 計算誤差
opt.zero_grad() # 導數重置
loss.backward() # 反向傳導
opt.step() # 優化器修正
plt.subplot(1, 2, 2)
y_p = forward(x).detach().numpy()
plt.plot(x, y_p)得到的如下圖

左邊 ( 正確答案 ) 和 右邊 ( 預測結果 ) 看起來有八成像了,用 y 約 0.5 做分界點, 落在 130 度左右的範圍
以上的範例中,我們從來沒有真正的去管 a, b 的實際數值多少,這就是 Machine Learning 厲害的地方,他會自己去找到答案
( 我們一直是用 y = ax + b 這個公式,上面範例也是一種最簡單的感知機 )
六、激勵函數之 Sigmoid / ReLU / Tanh / Softmax 比較
其實 relu, tanh, softmax 各有自己的應用場景,本文篇幅有限,我們無法在本篇說明實際的應用( 實際應用會於日後文章再說明)
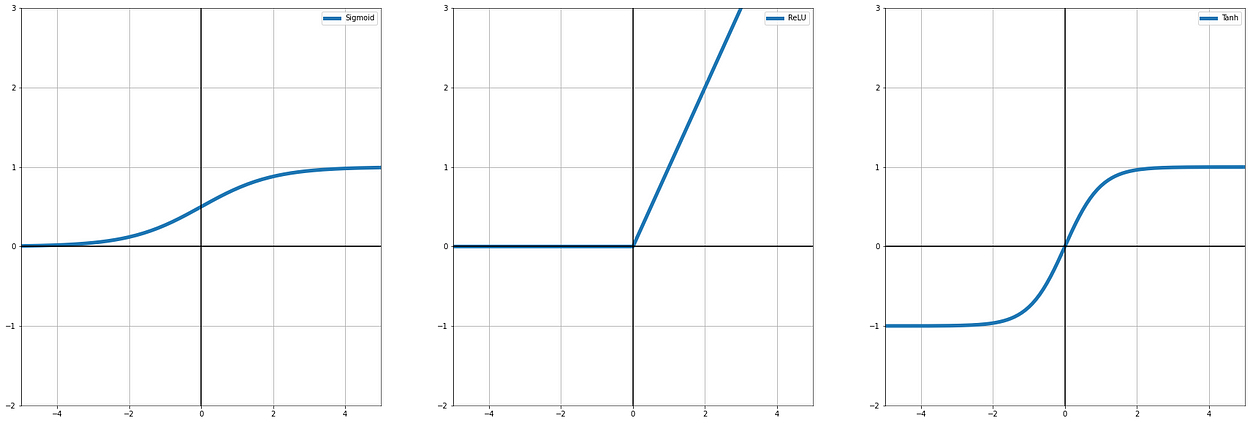
6.1 - ReLU, Tanh 和 Sigmoid 簡介
ReLU, Tanh 和 Sigmoid 其實差別就是輸出的範圍
- Sigmoid:上面提過,數字越大(正數),越趨近於 1,數字越小(負數),越趨近於 0,主要用在 0 / 1 的判斷場景,目前比較多的應用是放在輸出層 ( Deep Learning )
- ReLU:數字大於 0 ,就會是那個數字,如果小於 0 就會是 0 ,用程式碼來看就是 “if x > 0 then x else 0" 又或是 max(x, 0)
因為這個特性適合用在線性回歸的問題或是保留特徵值傳遞 ( Deep Learning ) - Tanh :和 Sigmoid 類似,但它的輸出範圍從 0 變成 -1,所以是 -1 與 1,不少場合使用 Tanh 會有更高的效率 ( 因為他比 Sigmoid 有更大的範圍可以傳遞資訊 )
看文字敘述不清楚的話,可以看看輸出範圍圖 ( 我們都假設 x 是 -5 ~ 5)
6.2 - Softmax 簡介
其中 Softmax 有些特別,他不是一個單純的計算,他適用於分類
( 例如物件辨識,手寫辨識… )
白話文的說,他是用來計算機率的,他會將輸入的數字給出對應的機率,該機率總和就是就是 1 ( 意即 100% )
例如,我們常常看到的物件辨識範例,可能會有
- 貓 70%
- 狗 25%
- 馬 5%
這個 0.70 + 0.25 + 0.05 = 1.00 就是 softmax 輸出的總和
他不管輸入的數值(x) 範圍是多少,就是會給出一個對應的 x 機率範圍
大家可以跑看看以下程式碼
x = torch.randn(30)
plt.stem(torch.softmax(x, dim=0))
print('總和:', torch.sum(torch.softmax(x, dim=0))) 類似下圖的東西 ( 因為是亂數,所以每次結果都不會相同 )
總和會是: tensor(1.0000)
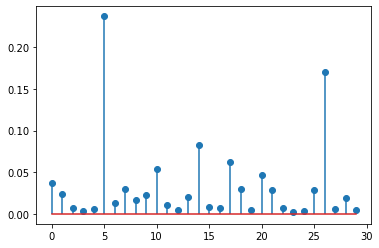
Softmax 会告诉我们哪个 x 发生的机率更大
而那个 x 怎么来的,我们可以透过 Machine Learning 找出来
所以用在图像识别方面的输出层很常见
七、小结
本文是激励函数的简介上篇,以上是很常用的激励函数 ( Activation Funcitons )
往后我们的 Deep Learning 基本上都脱离不了他们的概念,下篇我们会来看实际范例的应用 ( 下篇等本人有空再写.... )
另外激励函数使用需要注意的部分,有兴趣的读者可以多多研究
- 输出范围与传递信息问题
- 微分问题
- 选择正确的输出函数
Seachaos