背景：

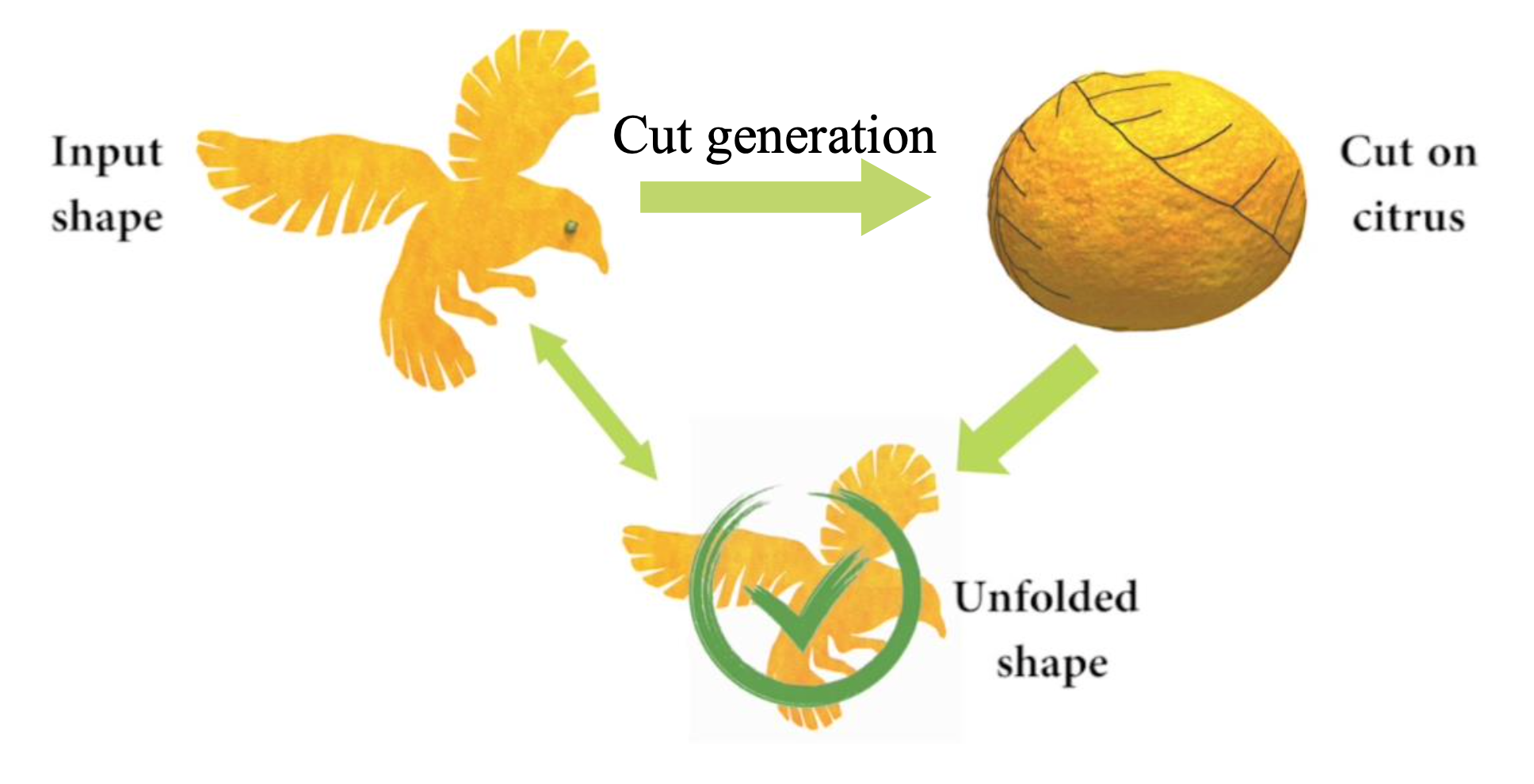
今天给大家介绍一篇中国科学技术大学发表的论文《Computational Peeling Art Design》。论文要解决是：如何把球状三维物体的表面连续展开成一些艺术画面，要求是展开表面要占三维物体表面整个面积，展开表面要和艺术体形状尽可能相似。

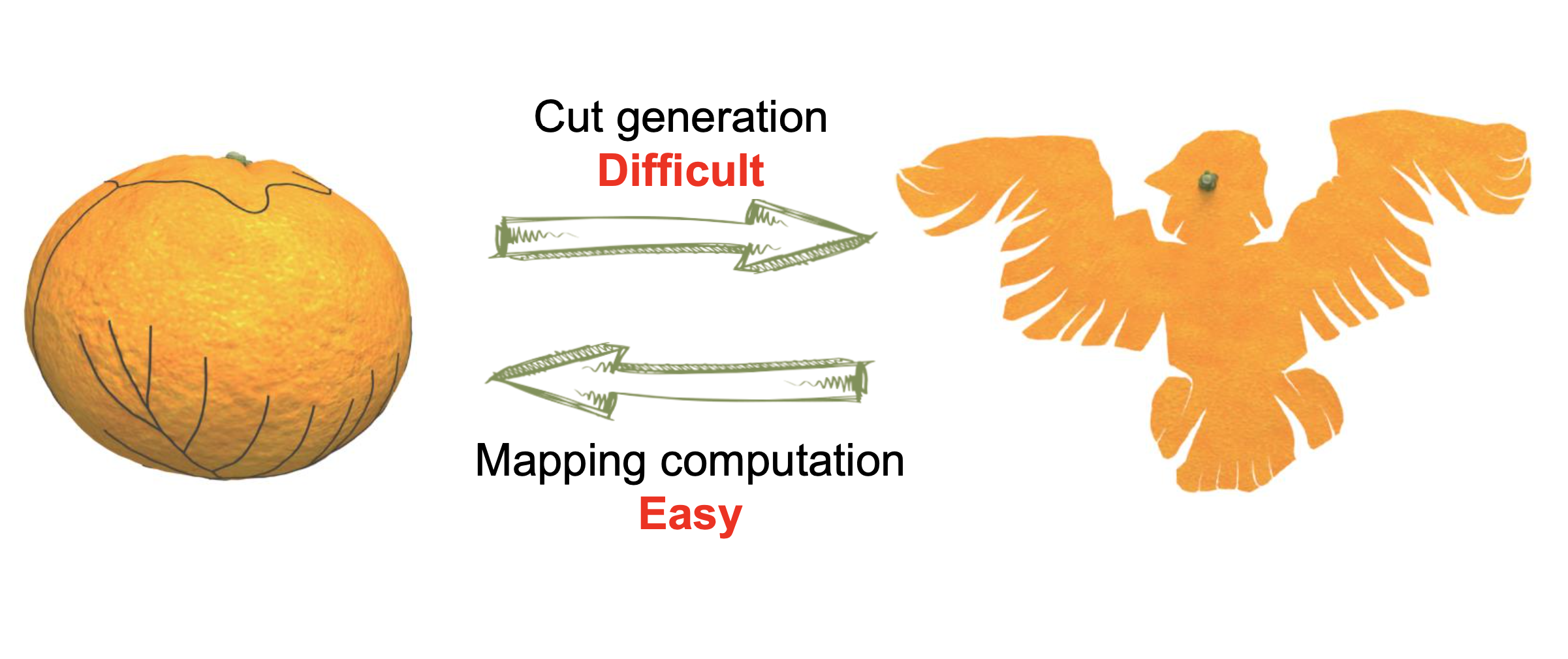
主要解决思路如下：

1.把艺术形状映射到三维表面

2.调整映射方程，改变艺术形状在三维表面的覆盖度

3.每次调整的方向为：让三维表面没被覆盖面积最小+展开表面要和艺术体形状尽可能相似

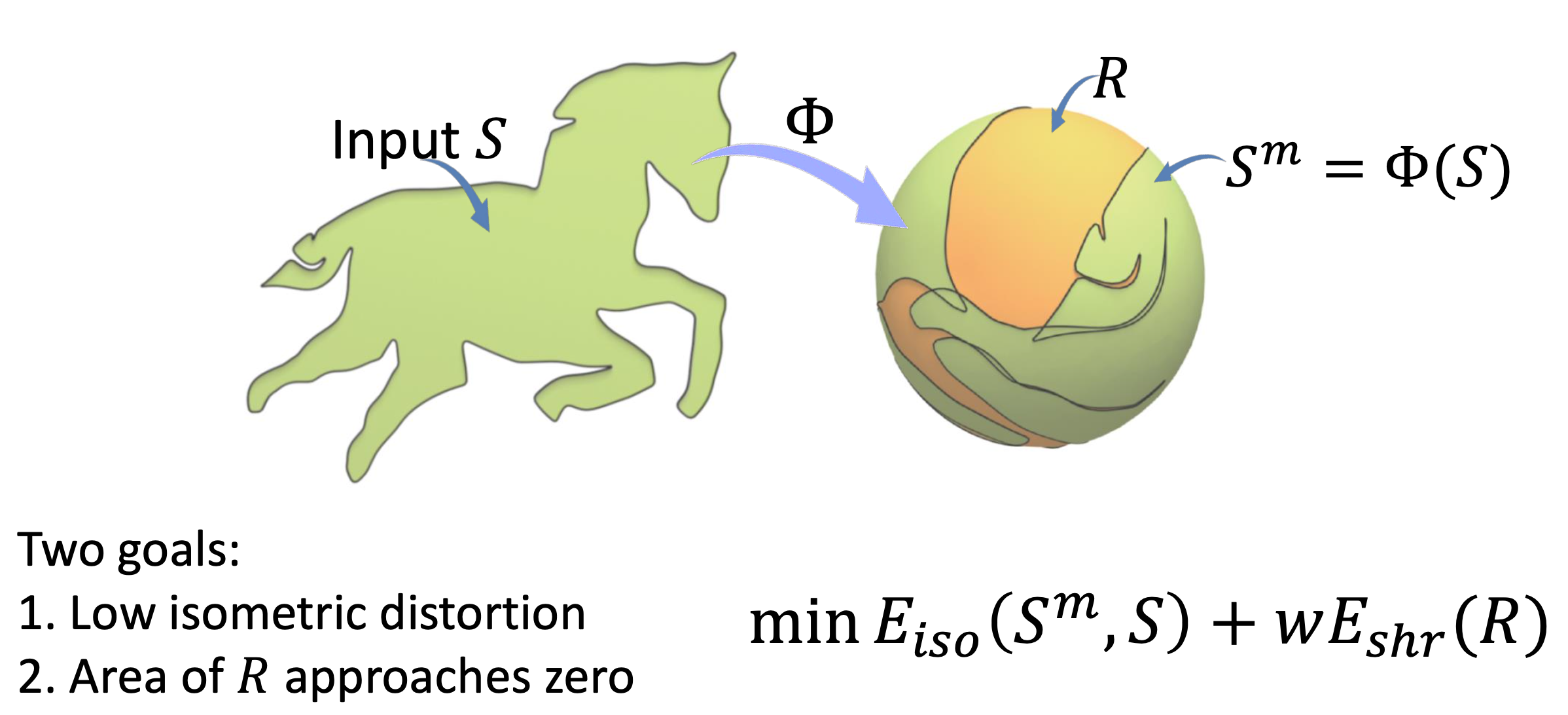
1. 低等距畸变：这意味着在从一个形状变换到另一个形状的过程中，保持了低等距畸变。等距畸变是指在形状变换中保持了点之间的距离关系。低等距畸变意味着变形后的形状与原始形状之间的点之间的距离差异很小，即变形是相对刚性的。

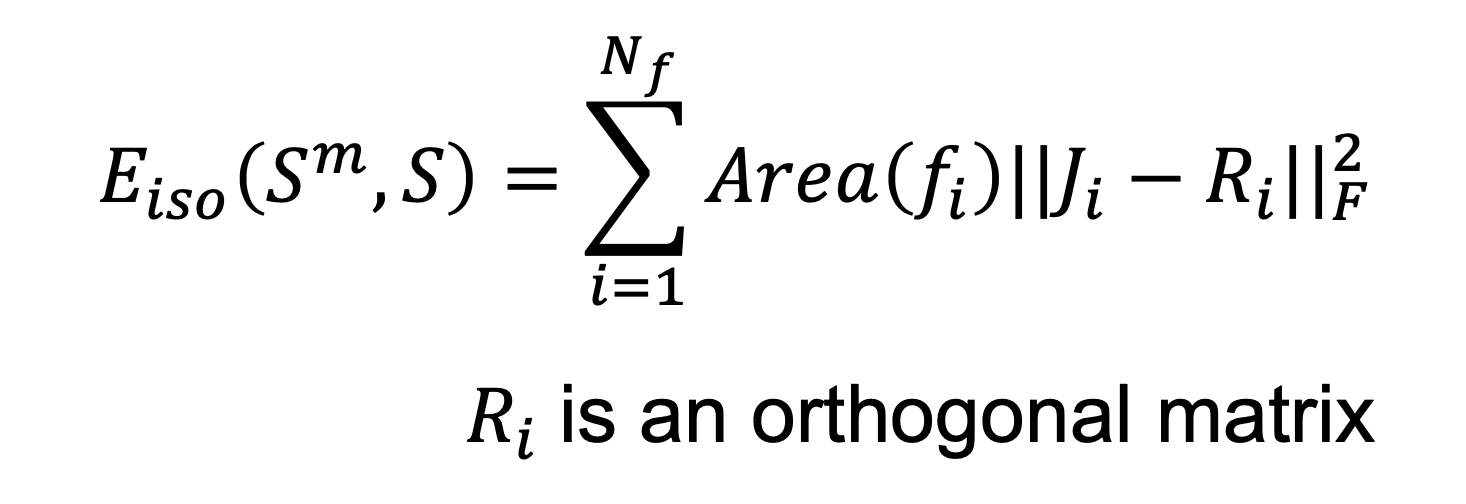
ARAP（As-Rigid-As-Possible，尽可能刚性）畸变度量是计算机图形学和几何处理领域中用于评估网格或表面在保持刚性的情况下从一种形状变换到另一种形状时的畸变或变形的度量标准。它特别适用于表面参数化、网格变形和形状插值等任务。

ARAP畸变度量的基本原理是在变形时保持局部刚性。它假设网格的小局部区域在变形过程中应尽可能保持刚性。该度量标准量化了变形后的形状与初始未变形形状之间刚性保持的偏差。

ARAP畸变度量的关键思想是比较变形网格中的角度和边长与原始未变形网格中对应的局部区域的角度和边长之间的差异，并尝试最小化这种差异。这有助于确保变形后的形状在局部刚性方面与原始形状尽可能接近。

ARAP畸变经常被用作优化问题中的能量项。通过最小化ARAP畸变能量，可以找到一个变形或参数化的网格，它在保持局部刚性的同时实现所需的形状变化。

总之，ARAP畸变度量是一种衡量网格变形或变换如何保持其局部刚性的度量标准，它在计算机图形学和计算机辅助设计中的各种几何处理任务中发挥着关键作用。

2. 𝑅的面积趋近于零：这表示区域 𝑅 的面积在优化过程中逐渐减小，接近于零。在文中，𝑅 是一个区域，通常是指一个在形状变换中需要被缩小或消失的区域。当𝑅的面积趋近于零时，意味着整个形状或区域已经基本被覆盖或填满，没有留下太多未覆盖的部分。这通常是优化目标的一部分，特别是在一些形状变换或映射问题中，我们希望形状能够完全覆盖或填充目标区域。

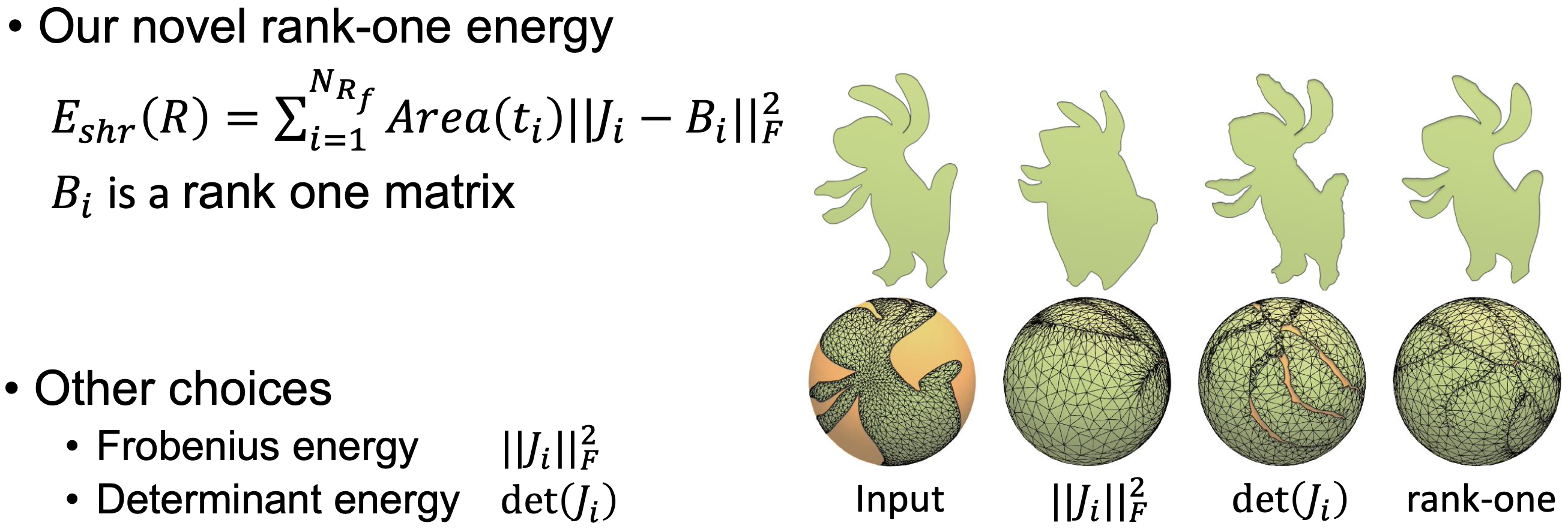
"Shrink energy"（缩减能量）是指在优化问题中使用的一种能量项或数学表达式，特别是在几何建模或形状优化的背景下。缩减能量的目的是在优化过程中鼓励或强制减小或缩小几何形状或结构中的某些区域。

在您提供的文本中，"shrink energy"在将2D形状映射到3D表面（柑橘水果）的优化过程中使用，同时最小化失真。这个能量项用于确保映射形状（𝑆𝑚）充分覆盖表面（𝑀）并减小未覆盖或重叠区域的面积。在这个上下文中，缩减能量的具体制定涉及最小化失真和某些区域的重叠，以实现所需的映射和覆盖。

缩减能量可以采取各种形式，具体取决于优化问题和目标。它通常涉及到与面积最小化、距离最小化或其他几何约束相关的数学表达，以实现所需的形状转换。缩减能量的确切制定方式因应用程序而异。

有了优化loss，输入要生成的艺术图片就可以开始迭代计算了，上面是对这个过程描述示意图。

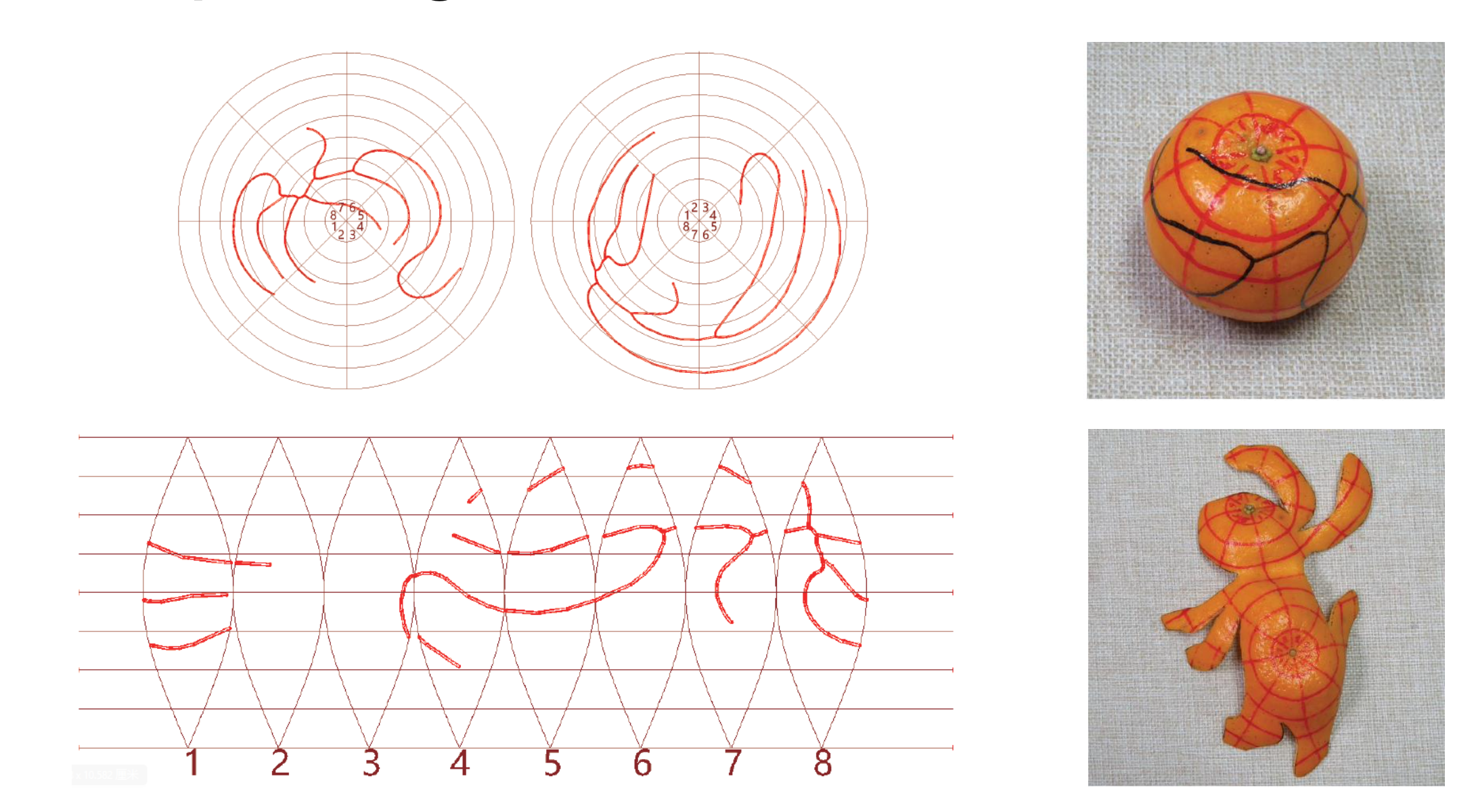
迭代计算得到自己想要的图形状后，接下来的工作就是把图画到真实的橘子上开始按图索骥剥出艺术图形。

为了画图的方便，科研案经纬划分的方式把橘子分成经纬图，然后把两极、和球纵面分8份方便定位绘制。

这部分作者给出了代码实现，但是代码源码没有开源，只给出了exe执行文件。这块后面尝试复现下代码，可以不只是在球状3d模型映射，还可以在方形、柱状...其它形状剥出艺术品。这在视觉商业上应该有不少应用，配合现在大火的AIGC可以完成很多新东西。

论文正文

翻译如下：

图1。由我们的设计系统生成的剥皮艺术作品。沿着柑橘水果上绘制的曲线进行制作（左上方），将柑橘水果展开成站在树枝上的鹦鹉（a），蜥蜴（b）或蕨类植物（c）。

Citrus Peeling Art是一种创意艺术形式，艺术家们将柑橘水果剥成各种优雅的2D形状，描绘动物、植物和卡通形象。这种艺术形式遵循保护原则，即每个形状必须使用整个果皮创建。在这种艺术中，关键是找到最佳的切割线，以便将柑橘水果切割并展开成所需的形状。然而，对于用户来说，想象并生成他们所需形状的切割线是非常困难的。因此，我们提出了一种用于柑橘剥皮艺术设计的计算方法。我们的关键见解是，我们不是解决困难的切割生成问题，而是将设计好的输入形状映射到柑橘水果上，以试图覆盖整个柑橘水果，并使用映射的边界来生成切割路径。有时，映射的形状无法完全覆盖柑橘水果。因此，我们开发了五种定制的交互方式，用于修正输入形状，使其适用于柑橘剥皮艺术。映射过程和用户交互是迭代进行的，以满足用户的设计意图。大量的实验，包括一项形式化的用户研究，证明了我们的方法在剥皮艺术设计和构建方面的能力和实用性。

ACM Reference Format: Hao Liu, Xiao-Teng Zhang, Xiao-Ming Fu, Zhi-Chao Dong, and Ligang Liu. 2019. Computational Peeling Art Design. ACM Trans. Graph. 38, 4, Article 64 (July 2019), 12 pages. Computational peeling art design | ACM Transactions on Graphics

1 引言 计算艺术可以帮助用户以算法和程序化的方式轻松可视化、设计和创建生成性艺术[Bickel et al. 2018; Wood et al. 2016]。柑橘剥皮艺术是由Yoshihiro Okada [Okada 2010]创造的，允许用户沿着指导线剥开柑橘水果，然后展开整个柑橘水果成为所需的2D形状，如图2所示。这种迷人的艺术形式为人们提供了享受和创造的机会，已广泛用于儿童教育中。 然而，到目前为止，只创作了有限数量的作品[Okada 2010]。要创建这种艺术形式的新样本，设计师需要富有想象力并进行大量的试错实验，这并不是一件简单的事情，而且非常耗时。因此，一般用户要将柑橘水果剥成定制的形状是非常具有挑战性的。

我们的目标是开发一种算法方法，帮助家庭用户为他们期望的输入形状创建切割路径和剥皮作品。从几何处理的角度来看，这个问题试图找到一种在柑橘水果上生成切割路径的方法，以展开它成为接近用户设计的2D形状。

现有关于计算表面切割路径的研究旨在最小化切割长度和展开形状的畸变[Lietal.2018; Poranneetal. 2017; Sharp and Crane 2018]；然而，我们提出的问题要困难得多。原因有两个。首先，很难获得一个可计算的度量标准，可以有效地用于优化，以测量展开形状与期望形状之间的接近度或相似度。其次，可能没有可能的切割路径，可以使展开的形状充分匹配给定的输入形状。用户应该能够修改输入形状以找到合适的解决方案。然而，创建一个易于使用的设计系统，允许用户自由修改输入形状并生成期望的结果并不是一件简单的事情。

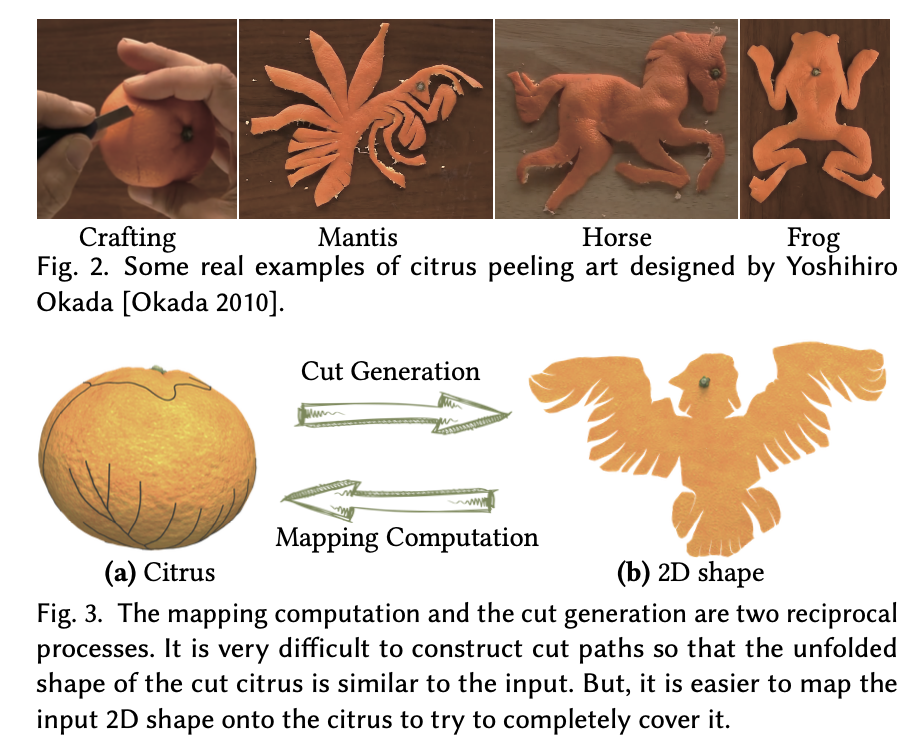
在本文中，我们提出了一种柑橘剥皮艺术设计的新方法。与其直接计算切割路径以满足形状相似性要求，我们从不同的角度研究了这个问题（如图3所示）。实际上，如果我们将一个展开的形状映射回柑橘水果，柑橘水果可以完全被覆盖，映射形状的边界代表了切割路径。因此，我们将输入形状映射到柑橘水果上，并尝试完全覆盖它。然后，根据映射输入形状的边界确定切割线。我们方法的关键见解在于将切割生成问题转化为更容易解决的映射问题。因此，我们提出了一种新方法，将输入形状映射到柑橘水果上，以获得低等距畸变，从而确保展开的形状与输入形状高度相似。

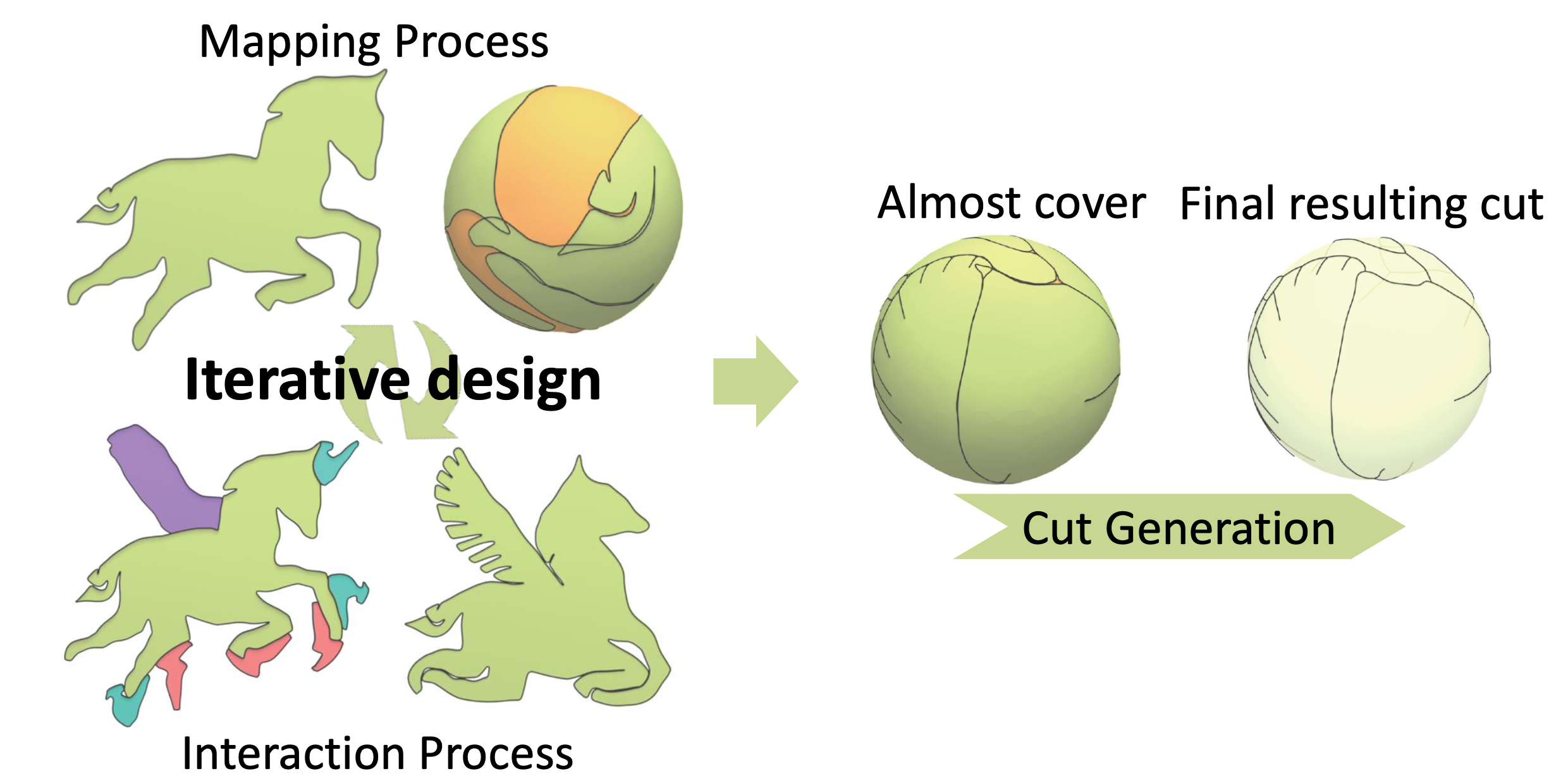
然而，仅使用这种低等距畸变映射并不总是适用于每个输入形状。为了修改适用于柑橘剥皮艺术的输入形状，我们将用户纳入设计过程中。基于对柑橘剥皮艺术原理的分析，我们提供了五种定制的交互方法，包括形状增强、角度增强、部分删除、曲率减小和预处理。然后，映射过程和交互交替进行，以满足用户的设计意图。图4显示了一个示例。

据我们所知，我们的方法是首个研究切割生成问题的方法，其中展开包含低等距畸变，并且展开的形状与期望的输入形状相似。提供的用于柑橘剥皮艺术设计和构建的计算工具能够创建优雅的形状。我们通过大量实验（60个示例）和形式化用户研究（10名参与者）来证明我们的技术的可行性和实用性。

相关工作

网格切割：以前的网格切割方法通常侧重于低扭曲和短切割路径的要求。一些方法首先检测可能引入高扭曲的顶点，然后使用最小生成树连接检测到的顶点，以确定切割路径[Chai et al. 2018; Sheffer 2002; Sheffer and Hart 2002]。开发了一种迭代算法，该算法交替展开网格并找到具有最大扭曲的顶点到现有边界的最短路径[Gu et al. 2002]。网格分割方法[Julius et al. 2005; Lévy et al. 2002; Sander et al. 2002, 2003; Zhang et al. 2005; Zhou et al. 2004]将输入网格划分为多个片段，每个片段可以以非常低的扭曲展开。一些方法同时优化切割长度和展开扭曲[Liet al. 2018; Poranne et al. 2017]。提出了一种全局变分方法来生成切割[Sharp and Crane 2018]。这些方法不能生成与输入形状类似的展开形状。

低扭曲映射：已经提出了许多用于低扭曲映射的方法（参见[Botsch and Sorkine 2008; Floater and Hormann 2005; Li and Iyengar 2015; Sheffer et al. 2006]的综述）。通常，计算低扭曲映射的任务被制定为一个优化问题，试图在一些指定的约束条件下最小化扭曲能量函数。为了保持映射的等距性，选择了等距扭曲能量进行优化。存在许多等距扭曲度量，如ARAP能量[Liu et al. 2008]、等距AMIPS能量[Fu et al. 2015]和对称Dirichlet能量[Smith and Schaefer 2015]。为了优化这些能量，已经提出了许多几何优化算法，包括局部/全局方法[Liu et al. 2008; Sorkine and Alexa 2007]、有界扭曲方法[Kovalsky et al. 2015; Lipman 2012]、基于表示的方法[Fu and Liu 2016; Sheffer and de Sturler 2001]、由粗到细的方法[Hu et al. 2018; Praun and Hoppe 2003]和基于维护的方法[Liu et al. 2018; Rabinovich et al. 2017]。Boundary First Flattening（BFF）方法[Sawhney and Crane 2017]可直接控制展开形状的边界长度或角度，但不研究切割生成问题。在我们的映射过程中，我们将ARAP能量与新颖的度量结合使用，稍微修改输入形状，有效缩小了不包括在映射区域内的某部分柑橘的范围。

图4展示了方法的工作流程，说明了如何将输入的2D形状映射到柑橘表面并进行交互，最终生成切割路径和展开的结果。(a) 图中展示了一个输入的2D形状S。(b) 图中展示了如何将输入形状S映射到整个柑橘M的表面。由于输入形状不适合柑橘果皮艺术，所以映射后的形状Sm（绿色部分）不能完全覆盖柑橘M。(c) 图中展示了将映射形状Sm和柑橘M上未覆盖的区域（图(b)中的橙色部分）展开到一个平面上进行交互。紫色、红色和青色区域表示用于交互的区域。(d) 在交互之后，生成了一个新的2D形状。映射过程和交互是迭代进行的，直到未覆盖区域的面积几乎为零或用户不再进行交互为止。(e) 图中展示了映射形状完全覆盖了柑橘。(f) 使用映射形状的边界生成最终的切割线C。(g) 将柑橘切割成一个展开到平面上的具有磁盘拓扑结构的网格。

这个工作流程说明了如何通过迭代映射和交互过程，将输入形状转化为适用于柑橘果皮艺术的形状，并生成相应的切割路径和展开结果。

可折叠艺术设计：最近提出了各种用于艺术设计的计算系统，包括可折叠艺术设计。这些系统通常涉及切割、弯曲和折叠表面片段以创建复杂的设计。例如，纸艺设计依赖于切割和折叠纸张表面。已经开发了一些工具，用于设计纸张弹出插图和线框网格。然而，本文的重点是柑橘剥皮艺术相关的计算挑战，目标是将柑橘水果剥成2D形状，这与传统的可折叠艺术设计问题不同。

这一部分讨论了关于柑橘果皮艺术设计的提出方法及其公式化，重点强调了涉及柑橘果皮艺术设计的关键思想和挑战，并介绍了优化过程中使用的关键能量项。

第一段提到了与网格切割、折纸术和可折叠艺术设计相关的先前工作。它强调了现有的用于展开3D网格的方法不能确保折叠后的形状与用户所期望的输入形状相匹配。所提出的方法旨在计算柑橘上的切割路径，以实现这一目标。

第二段介绍了问题和挑战，即在将2D形状（S）映射到零亚属的柑橘表面（M）上时，确保展开后的形状（Sc）与输入形状（S）紧密相似。目标是最小化两个2D形状之间的相似性误差（Esim），考虑到展开操作（Ψ）。挑战在于选择一个适当的相似性度量标准以及如何处理形状之间的对应关系。

第三段介绍了方法的关键思想，其中将Sc以低等距畸变映射回M，以实现M的完全覆盖。映射后的Sc的边界类似于切割线C。根据这一事实，可以将S映射到M并尝试完全覆盖M。如果M完全覆盖，映射后的S的边界近似于所需的切割线C。这是方法的关键思想：将切割生成问题转化为更容易解决的映射问题。

第四段概述了方法的目标和公式化。它将从S到其在M上的映射形状Sm的映射表示为Φ，即Sm = Φ(S)。目标是计算Sm，使其与S之间的等距畸变较小，并确保完全覆盖M而没有重叠。公式化的过程如下：

min Eiso(Sm, S) + ωEshr(R), (2) 

Sm其中Eiso(Sm, S)表示从S到Sm的等距畸变。R（见图4（b）中的橙色区域）表示与Sm具有相同边界并包含M \ Sm的区域。Eshr(R)是用于缩小R并解决Sm重叠的能量，即尝试使Sm完全覆盖M的能量。ω是平衡这两个项的正权重。

第五段解释了方法中使用的等距畸变能量，它使用ARAP畸变度量来衡量Eiso(Sm, S)。它涉及到仿射变换和雅可比矩阵以计算畸变能量。

第六段讨论了缩小能量，其目标是退化三角形区域以解决重叠问题并确保完全覆盖。此处引入的能量项基于秩-1能量概念，并涉及到用于在秩-1矩阵空间上投影Ai的辅助变量。

这些段落提供了关于方法公式化的概述，强调了柑橘果皮艺术设计中涉及的关键思想和挑战。

等距畸变能量。我们使用ARAP（As-Rigid-As-Possible）畸变度量 [Liu et al. 2008] 来衡量 Eiso(Sm, S)。通过在fi上引入本地坐标系Fmi，从fi到fim（映射形状中的对应三角形）的映射被视为一个二维仿射变换，由一个记为Ji的2×2雅可比矩阵描述。

等距畸变能量Eiso(Sm, S)的计算如下：

Eiso(Sm, S) = Σ Area(fi) * ∥Ji - Ri∥F2，对于fi ∈ F

这里：

• Area(fi)代表三角形fi的面积。
• ∥·∥F2表示Frobenius范数。
• Ri是一个辅助变量，表示Ji在二维旋转群上的最接近投影。

缩小能量。我们对R进行三角化，得到一个具有一组顶点Vr = {vri} 和三角形F r = {fir}的三角形网格。每个fir都配备了一个本地坐标系统Fri。我们的目标是退化每个fir。一个天真的选择是使用fir的面积作为优化映射的附加能量项。然而，这种方法效果不佳（请参见图10中的比较）。假设存在一个边长为1的2D正三角形t，从t到fir（在Fri中）的映射是一个带有2×2雅可比矩阵的仿射变换，表示为Ai。然后，fir的零面积要求被转化为对Ai的秩为一的要求。基于这个概念，我们提出了一种新的秩一能量：

Eshr(R) = Σ Area(t) * ∥Ai - Bi∥F2，对于fir ∈ Fr

这里：

• Area(t)代表正二维三角形的面积。
• ∥·∥F2表示Frobenius范数。
• Bi是一个辅助变量，表示Ai在秩一的2×2矩阵空间上的最接近投影。

这个收缩能量鼓励优化过程缩小橙色区域，确保映射形状Sm完全覆盖柑橘表面。

重构。我们将R的边界表示为∂R，将Sm的边界表示为∂Sm。∂R和∂Sm始终相同。映射问题可以重新表述为以下问题：

求解器。我们将Vm和Vr收集到一个集合中，表示为V = {vi}。同样，F := {fi}。fi的局部坐标系表示为Fi。由于Eshr(R)的形式与Eiso(Sm,S)类似，我们采用局部-全局求解器[Liu et al. 2008]来解决(5)。

• 局部步骤。假设bvk是固定的，每个三角形都会计算局部坐标系Fi和Ri（或Bi）。Ri的计算方法与[Liu et al. 2008]相同。我们将Ai = UiSiViT表示为Ai的奇异值分解，其中Si = diag(σi，τi)是带有奇异值的对角矩阵。然后，当Ai给定时，我们计算Bi = Ui diag(σi，0)ViT。选择这种类型的Bi，实际上是在最小化τi2。

• 全局步骤。假设Ri，Bi，Fi是固定的，我们首先更新bvk，然后将它们投影到M上。

与[Liu et al. 2008]不同，我们的变量是3D顶点bvk。因此，在全局步骤中Fi也会发生变化。解决全局步骤很困难，因此我们设计了一个近似方法。

首先，假设全局步骤中Fi是固定的。其次，bvk的运动在局部上被近似为一个2D向量。我们将bvk的局部坐标系表示为Fvk，并将Fvk的第三轴设置为bvk的法线。然后，bvk的运动δbvk是Fvk中的一个3D向量。我们限制δbvk在bvk的切平面内，表示其第三分量为0。对于bvk的一环邻居中的一个三角形bfki，其局部坐标系被表示为Fik，而bvk在Fik中的运动为δbvik。我们使用δbvk和δbvik来近似2×2矩阵Ji和Ai。然后，问题仍然具有二次目标函数和一些线性等式约束（即∂R = ∂Sm），因此我们解其线性KKT系统以获得运动δbvk。由于运动δbvk通常很小，在实践中这种近似方法效果很好。为了尽量减小失真，我们设置ω = 0.001。图5显示了一个示例。

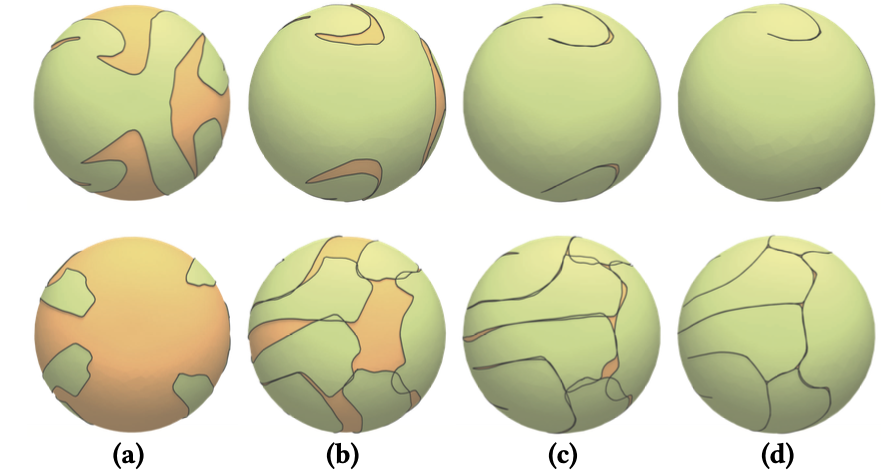
图5. 我们在Frog形状上进行优化的渐进结果（图6 (a)）。 （a）初始化。 （b）第10次迭代后。 （c）第75次迭代后。 （d）255次迭代后的最终结果。 我们在第一行和第二行分别显示了柑橘的正面和背面视图。

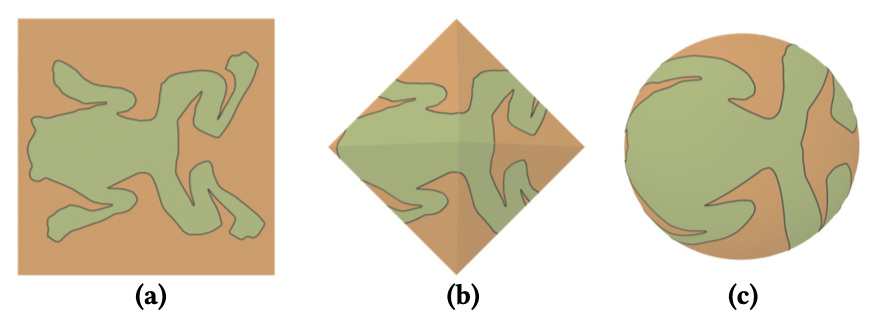
图6. 初始化过程。我们首先将输入形状放入一个正方形中（a）。然后，我们将正方形映射到一个正八面体上（b）。最后，我们将八面体映射到M上以初始化映射形状（c）。在（c）中，绿色和橙色部分分别表示初始的Sm和R。在（c）中，我们为了可视化将M缩放了2.5倍。

初始化。要初始化Sm，一种直接的解决方案是使用立体投影；然而，这通常会产生较大的失真，因此需要更多的迭代来解决（5）。我们使用一个正八面体（表示为O）作为中间域（图6（b））。我们首先将S映射到O上以生成Se，然后根据O和M之间的一对一对应关系，将Se映射到M上以生成初始的Sm。正如我们所知，正八面体可以被展开成一个失真较小的正方形（参见[Praun和Hoppe 2003]的图6）。因此，我们将S放入一个正方形中并居中，然后可以轻松计算Se（图6）。由于初始的Sm没有重叠，所以初始的R就是M \ Sm。在我们的实验中，正方形的边长设置为max{αwS,αhS}，其中wS和hS分别是S的边界框的宽度和高度。为了产生更新Sm的自由空间，在我们的实验中，我们设置α = 1.05。如果S可以映射以完全覆盖M，那么它们的面积是相等的。基于这一考虑，我们初始化M的比例。

终止。我们的算法在目标函数值的相对误差小于10^(-4)或Area(R) < εa时终止。在我们的实验中，我们设置εa = 10^(-2)Area(M)，并且我们没有观察到任何不收敛的示例。

动态重网格。在优化过程中，R的网格质量通常会恶化，这会影响收敛速度。受[Jiang et al. 2017]的启发，我们使用[Botsch和Kobbelt 2004]动态重网格R。执行三个全局步骤后，我们进行一次重网格步骤。如图7所示，这次重网格是必要的。

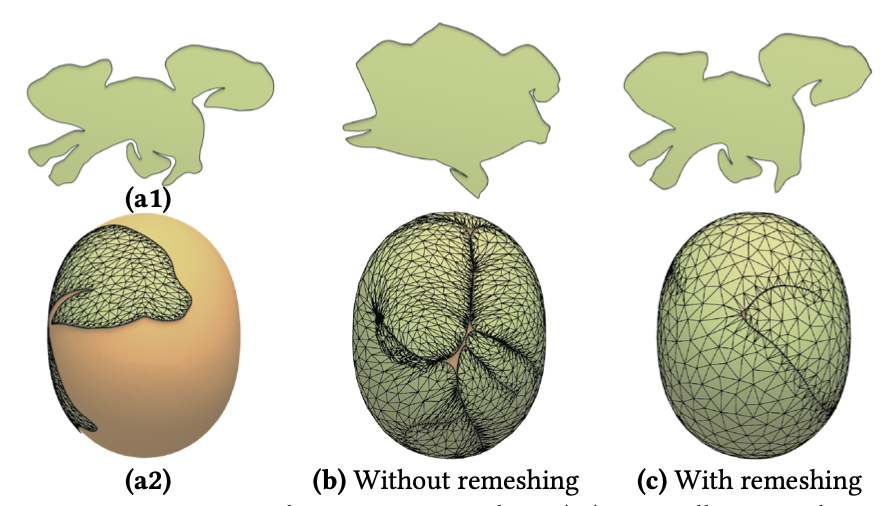
图7. 动态重网格。首先将2D输入形状（a1）映射到柑橘（a2）。在最后两列中，第二行显示了生成的Sm，而展开的形状在第一行。

Cut generation

如果输入形状S适合于柑橘剥皮艺术，则在解决（5）后R的面积非常小。我们使用∂R来计算切割线C。

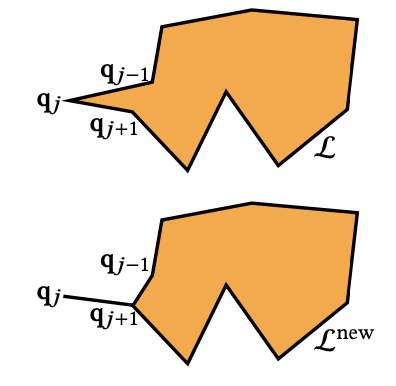
折叠。我们构建C的方法基于一个称为折叠的操作（见右侧插图）。折叠操作在包含m > 3个顶点的环L上定义，这些顶点按逆时针顺序定义，并且它们会周期性地扩展。也就是说，对于qj的qj = qj + km，对于所有k∈ Z。折叠操作在顶点qj处定义，并且我们选择与qj相邻的一个边qjqi（例如，右侧插图中i = j + 1）进行操作。执行折叠操作后，顶点qj消失，边qjqi被合并成一个新的边。这个操作通过使新边的长度等于qjqi的长度来实现。通过连续应用折叠操作，可以构建切割线C。

在顶点qj沿着边qj qi上执行折叠操作后，我们得到一个新的环Lnew，并且边qj qi被添加到切割线中。我们递归地在环上应用折叠操作，直到新的环包含三个顶点。对于这三个表示三角形的顶点，我们选择两条较短的边添加到切割线中。

在给定一个环L时，需要找到应用折叠操作的顶点。事实上，如果qj处的内角等于零，这表明其相邻较短的边之一属于C。因此，每次我们选择具有最小内角的顶点来执行折叠操作，沿着其较短的相邻边进行操作。

细节。在我们的实验中，初始环是∂R。由于重叠的存在，内角可能是负的，因此我们使用内角的绝对值作为标准。由于C由∂R的部分边界边组成，它可能不是平滑的。在我们的实验中，我们对C的顶点进行了五次拉普拉斯平滑操作，同时固定那些度数不等于2的顶点。我们在图4（f）中展示了一个示例。

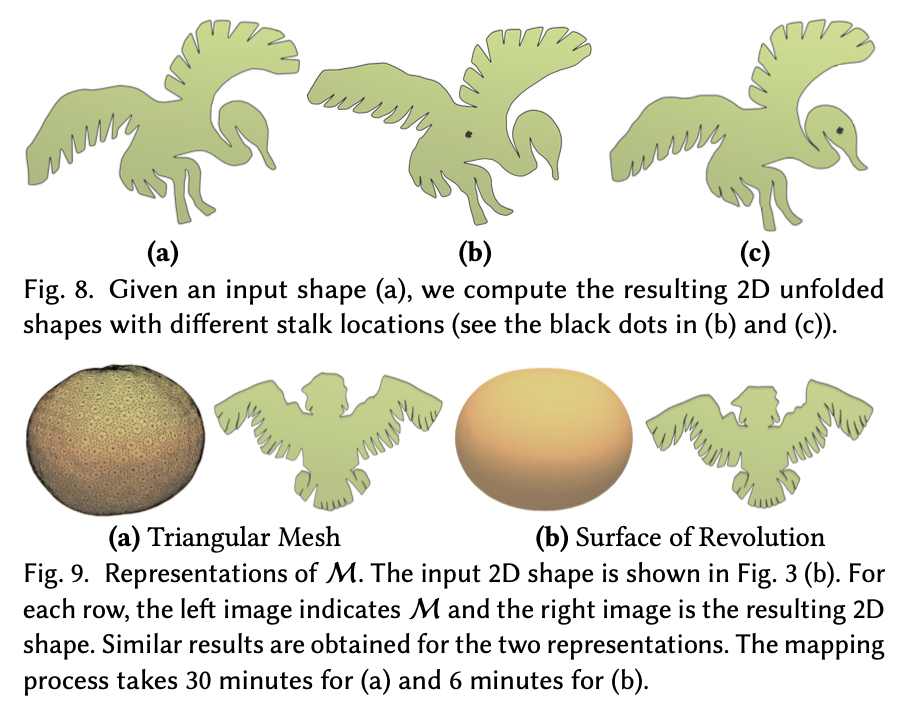
M的表示。M看起来像一个扁平的球体，所以我们默认将其近似为以原点为中心的旋转曲面。其中的一个点（x，y，z）可以表示如下：

x = r(φ)cos(θ)cos(φ)

y = r(φ)sin(θ)cos(φ)

z = r(φ)sin(φ)

这个表示中，r(φ)表示随着φ变化的半径，θ表示与x轴的角度，φ表示与z轴的角度。这种表示允许M的形状随着φ的变化而改变，从而能够适应不同形状的柑橘水果。

在这段文字中，作者描述了一些实现细节和讨论，包括表征M（柑橘水果的形状）、用于缩小R的能量、以及在切割生成过程中使用中轴线的可能性。

1. M的表示：M被描述为一个表面旋转的球体，作者提供了一个具体的参数表示，允许M的形状随着φ的变化而改变。这种表示允许适应不同形状的柑橘水果，并且在映射过程中使用径向投影将更新的顶点投影回M。

2. M的精确表示：为了更准确地表示M，可以使用高精度扫描仪扫描真实的柑橘水果并将其重建为三角形网格。在映射过程中，可以调整M的初始比例以确保包含与S相同的面积。然后使用最近点投影将更新的顶点投影回M。然而，这种方法成本高昂且不适用于普通用户。

3. 区域收缩能量：文章提到了一些其他可用于缩小R的能量，如detAi或∥Ai∥F2。然而，作者的rank-one能量效果更好，因为它产生了更小的畸变映射。

4. 中轴线：在切割生成过程中，可以使用R的中轴线作为最终的切割。这种方法速度快且鲁棒性强，适用于实际应用。

总的来说，这些细节和讨论提供了关于算法实现和可行性的重要信息，以及选择柑橘水果的不同表示方式的考虑。

小结：

这篇论文介绍了一种用于将球状三维物体的表面连续展开成艺术画面的计算方法，要求展开表面要占三维物体表面整个面积，展开表面要和艺术体形状尽可能相似。论文提出了低等距畸变和缩减能量的概念，并介绍了如何将2D形状映射到3D表面并使用缩减能量来确保映射形状充分覆盖表面并减小未覆盖或重叠区域的面积。论文还提供了代码实现，并探讨了该技术在视觉商业上的应用。 本文提出了一种新的算法方法，用于帮助用户为他们期望的输入形状创建切割路径和剥皮作品。该方法将切割生成问题转化为更容易解决的映射问题，并使用低等距畸变映射来确保展开的形状与输入形状高度相似。为了修改适用于柑橘剥皮艺术的输入形状，本文提供了五种定制的交互方法，并使用大量实验和形式化用户研究来证明该技术的可行性和实用性。

本文介绍了如何将2D形状映射到柑橘表面，以生成适用于柑橘果皮艺术的形状，并生成相应的切割路径和展开结果。该方法的关键思想是将切割生成问题转化为更容易解决的映射问题，并使用等距畸变能量来优化映射过程。该方法使用ARAP畸变度量来衡量等距畸变，并使用局部/全局方法、有界扭曲方法、基于表示的方法、由粗到细的方法和基于维护的方法来优化等距畸变能量。该方法的工作流程包括将输入形状映射到柑橘表面并进行交互，最终生成切割路径和展开结果。该方法的目标是计算柑橘上的切割路径，以实现这一目标。