目录
一:TensorFlow简介
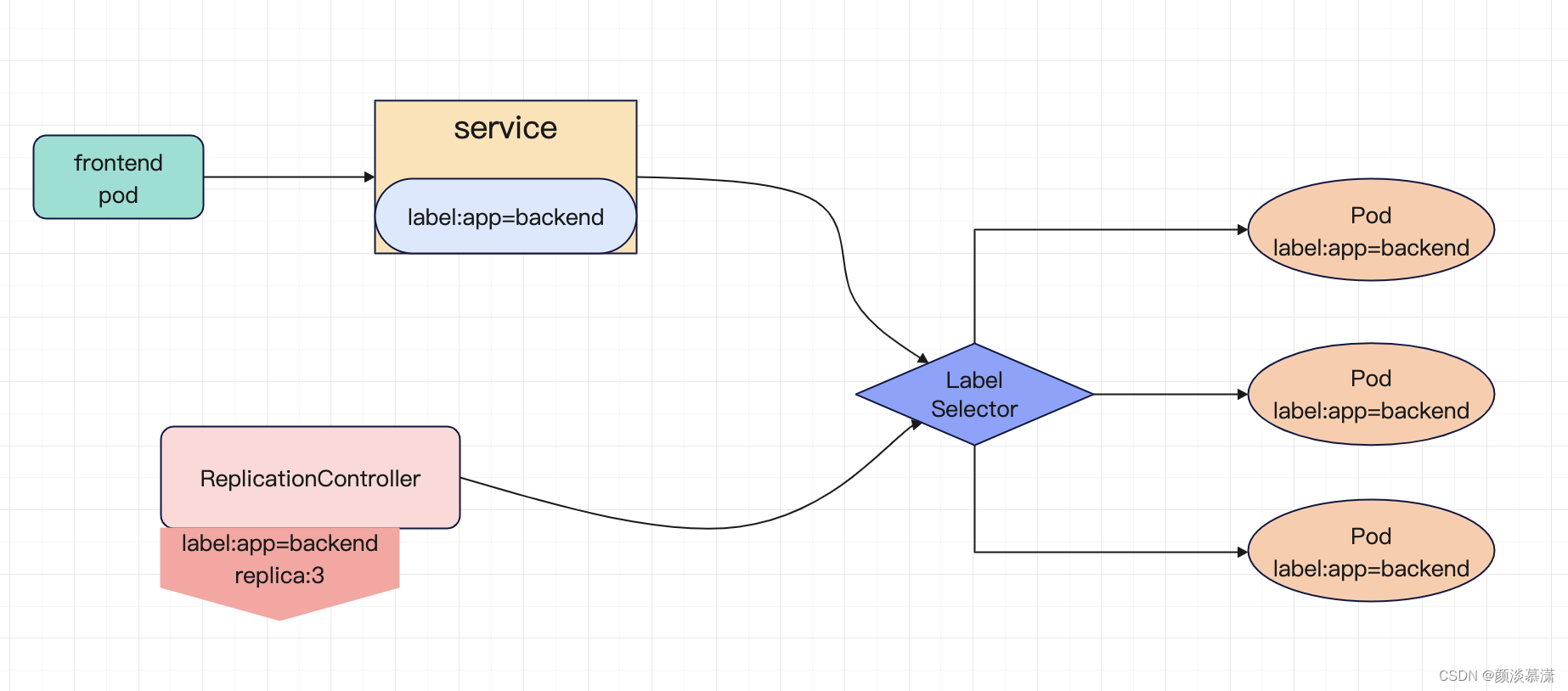
二:TensorFlow工作形式
三:图/Session
四:安装tensorflow
五:张量
六:变量/常量
七:创建数据流图、会话
八:张量经典创建方法
九:变量赋值、初始化操作
十:占位符
十一:TensorFlow求解二元一次方程
一:TensorFlow简介
TensorFlow由谷歌人工智能团队谷歌大脑(Google Brain)开发和维护,是一个基于数据流编程(dataflow programming)的符号数学系统。被广泛应用于各类机器学习算法的编程实现,它支持GPU和TPU高性能数值计算,被广泛应用于谷歌内部的产品开发和各个领域的科学研究,对C和python支持的比较友好
二:TensorFlow工作形式
TensorFlow是采用数据流图(data flow graphs)来计算,所以首先我们得创建一个数据流流图,然后再将我们的数据(数据以张量(tensor)的形式存在)放在数据流图中计算,节点(Nodes)在图中表示数学操作,图中的线(edges)则表示在节点间相互联系的多维数据数值,即张量(tensor),训练模型时tensor会不断的从数据流图中的一个节点flow到另一个节点
三:图/Session
tf.Graph/图:用来定义运算流程,它与实际计算没有关系,只是勾画出计算流程,它不存储任何计算的值或者中间变量
tf.Session/会话:用来根据graph来进行实际运算,会分配资源,创建变量,并且保存变量的中间值以及结果
tensorflow的运算都必须在一个指定的session里进行
四:安装tensorflow
安装命令如下
pip install tensorflow==1.14.0 -i https://pypi.tuna.tsinghua.edu.cn/simple --user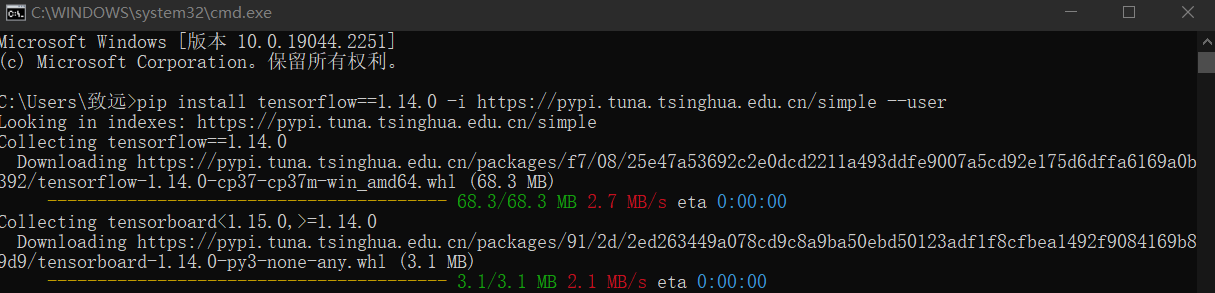
pip list检查是否安装成功

五:张量
张量tensor有多种,零阶乘张量为纯量或标量(scalar) 也就是一个数值,比如[1]
一阶张量为向量(vector),比如一维的[1,2,3]
二阶张量为矩阵(matrix),比如二维的[[1,2,3],[4,5,6],[7,8,9]]
以此类推,还有三阶三维的
张量创建的方法:
tf.ones
tf.ones_like
tf.zeros
tf.zeros_like
tf.convert_to_tensor(a)全1矩阵,如下
import tensorflow as tf
# 使用默认图
tensor = tf.ones((2, 2), dtype=tf.float32)
# 开启会话、启动图
with tf.Session() as sess:
print(sess.run(tensor))
输出结果:
[[1. 1.]
[1. 1.]]全0矩阵,如下
import tensorflow as tf
# 使用默认图
tensor = tf.zeros((2, 2), dtype=tf.float32)
# 开启会话、启动图
with tf.Session() as sess:
print(sess.run(tensor))
[[0. 0.]
[0. 0.]]创建一样的张量 ,如下
import tensorflow as tf
# 使用默认图
tensor = tf.zeros((2, 2), dtype=tf.float32)
tensor_like = tf.zeros_like(tensor)
# 开启会话、启动图
with tf.Session() as sess:
print(sess.run(tensor))
print(sess.run(tensor_like))
[[0. 0.]
[0. 0.]]
[[0. 0.]
[0. 0.]]
转换为张量,如下
import tensorflow as tf
import numpy as np
# 使用默认图
tensor = tf.zeros((2, 2), dtype=tf.float32)
tensor_like = tf.zeros_like(tensor)
np_ones = np.ones([3, 2])
tensor_ones = tf.convert_to_tensor(np_ones)
# 开启会话、启动图
with tf.Session() as sess:
# print(sess.run(tensor))
# print(sess.run(tensor_like))
print(sess.run(tensor_ones))
[[1. 1.]
[1. 1.]
[1. 1.]]六:变量/常量
变量Variable 定义语法
state = tf.Variable()
state = tf.Variable(0,name='counter')常量constant 定义语法
matrix1 = tf.constant([[3,3]])如下示例
import tensorflow as tf
# 1变量a
a = tf.Variable(0, name='a')
# 2常量b
b = tf.constant(1)
# 矩阵相加 实现加法模块
value = tf.add(a, b)
print(value)
输出结果如下:在实现加法模块OP后,就转为张量
Tensor("Add:0", shape=(), dtype=int32)OP:add加法、assign赋值、multiply乘法等
七:创建数据流图、会话
import tensorflow as tf
# 创建数据流图
graph = tf.Graph()
# 基于数据流图
with graph.as_default():
# 添加OP
var = tf.Variable(12, name='foo') # 创建变量
init = tf.global_variables_initializer() # 初始化所有变量
ass = var.assign(24)
# 创建一个会话,绘制启动的图
with tf.Session(graph=graph) as sess:
sess.run(init) # 如果图中有变量,必须执行初始化变量操作
sess.run(ass) # 执行OP 赋值
print(sess.run(var)) # 获取变量最终的值
输出结果值:24
八:张量经典创建方法
def random_normal(shape,
mean=0.0,
stddev=1.0,
dtype=dtypes.float32,
seed=None,
name=None):“服从指定正态分布的序列”中随机取出指定个数的值
shape:输出张量的形状,必选
mean:正态分布的均值,默认为0
stddev:正态分布的标准差,默认为1.0
dtype:输出的类型,默认为tf.float32
seed:随机数种子,是一个整数,当设置之后,每次生成的随机数都一样
示例如下
import tensorflow as tf
tf_random = tf.random_normal((3, 4), mean=0.0, stddev=1.0, dtype=tf.float32, seed=666, name='normal')
# 使用默认图
# 开启会话、启动图
with tf.Session() as sess:
print(sess.run(tf_random))
输出结果如下
[[-0.15161146 -0.6076202 -0.5504767 -1.3674356 ]
[ 2.4222426 0.30945507 -1.6234491 -0.3828629 ]
[ 1.190534 1.1368927 0.45719737 -0.50563335]]九:变量赋值、初始化操作
如下,把value值,赋值给变量a
import tensorflow as tf
# 1变量a
a = tf.Variable(0, name='a')
# 2常量b
b = tf.constant(1)
# 矩阵相加 实现加法模块
value = tf.add(a, b)
# print(value)
# 变量赋值操作:把value赋值给a
update_op = tf.assign(a, value)
# 变量初始化
init = tf.global_variables_initializer()
# 开启会话,启动图
with tf.Session() as sess:
sess.run(init)
sess.run(update_op)
print(sess.run(a))
输出结果:1 (实现了加法模块OP)
下面示例为,求10个数的和
import tensorflow as tf
# 1变量a
num_var = tf.Variable(0, name='num_var')
sum_var = tf.Variable(0, name='sum_var')
# 2常量b
b = tf.constant(1)
# 矩阵相加 实现加法模块
value = tf.add(num_var, b)
# 变量赋值操作:把value赋值给a
update_num = tf.assign(num_var, value)
# 加法OP
value1 = tf.add(sum_var, update_num)
# 赋值给sum
assign_op = tf.assign(sum_var, value1)
# 变量初始化
init = tf.global_variables_initializer()
# 开启会话,启动图
with tf.Session() as sess:
sess.run(init)
for i in range(10):
sess.run(assign_op)
print(sess.run(num_var))
print(sess.run(sum_var))
10个数的求和为55,如下
10
55十:占位符
占位符 placeholder
import tensorflow as tf
import numpy as np
# 定义占位符
inp1 = tf.placeholder(np.float32)
inp2 = tf.placeholder(np.float32)
# 矩阵乘法OP
outinput = tf.multiply(inp1, inp2)
# 开启会话,启动图
with tf.Session() as sess:
# feed_dict 对占位符赋值 格式是字典
print(sess.run(outinput,
feed_dict={inp1: [8], inp2: [7]}))
print(sess.run(outinput, feed_dict={
inp1: [8.5, 6],
inp2: [7, 8.5]
}))
输出结果如下:
测试输出1为:8*7=56
测试输出2为:8.5*7=59.5 与 6*8.5=51
[56.]
[59.5 51. ]十一:TensorFlow求解二元一次方程
import tensorflow as tf
import numpy as np
# 1/1+e^-(w*x+b) 求w b
# 简单LR 特征和标签只有一个 wb只有一组
# w b是变量 x y是占位符
# 1 占位符
x = tf.placeholder(tf.float32) # 特征
y = tf.placeholder(tf.float32) # 标签
# 2 变量
w = tf.Variable(tf.random_normal([1], name="weight"))
b = tf.Variable(tf.random_normal([1], name="bias"))
# 3 OP准备 1/1+e^-(w*x+b)
# sigmoid y=1/1+exp(-x)
y_predict = tf.sigmoid(tf.add(tf.multiply(x, w), b))
# 4 构建损失函数
num_samples = 400 # 数据样本数量
# pow幂计算(num,幂指数) cost损失值
cost = tf.reduce_sum(tf.pow(y_predict - y, 2.0)) / num_samples
# 5 梯度下降算法 求解最小损失值:AdadeltaOptimizer梯度算法(优化器)
Qptimizer = tf.train.AdadeltaOptimizer().minimize((cost))
# 6 初始化变量
init = tf.global_variables_initializer()
xs = np.linspace(-5, 5, num_samples)
ys = np.sign(xs)
# print(xs,ys)
cost_pre = 0
# 开启会话,启动图
with tf.Session() as sess:
sess.run(init)
# 训练 解方程
for i in range(200):
# 从x,y中准备好数据,给优化器,存入占位符
for xa, ya in zip(xs, ys):
sess.run(Qptimizer, feed_dict={x: xa, y: ya})
train_cost = sess.run(cost, feed_dict={x: xa, y: ya})
print(train_cost)
if train_cost - cost_pre < 1e-6:
break
print('w is', sess.run(w, feed_dict={x: xa, y: ya}))
print('b is', sess.run(b, feed_dict={x: xa, y: ya}))
输出结果,如下
0.00035491146
0.00035427077
0.00035353724
0.00035277064
0.00035199235
0.0003512103
0.00035042796
0.00034964643
0.00034886657
0.00034808862
0.0003473124
0.00034653812
0.00034576587
0.00034499532
0.00034422686
0.00034346027
0.00034269574
0.00034193308
0.0003411722
0.0003404133
0.00033965625
0.00033890113
0.0003381478
0.00033739654
0.00033664698
0.00033589936
0.00033515345
0.0003344097
0.0003336676
0.00033292745
0.00033218917
0.00033145258
0.00033071788
0.00032998514
0.00032925405
0.0003285247
0.00032779737
0.00032707173
0.00032634786
0.00032562588
0.0003249055
0.00032418716
0.00032347057
0.00032275572
0.0003220425
0.00032133138
0.00032062197
0.00031991414
0.00031920813
0.00031850397
0.00031780152
0.00031710084
0.00031640186
0.00031570476
0.0003150092
0.0003143154
0.00031362352
0.00031293323
0.00031224458
0.00031155781
0.00031087277
0.0003101895
0.00030950786
0.000308828
0.0003081499
0.00030747353
0.00030679905
0.00030612614
0.00030545497
0.00030478564
0.00030411806
0.00030345222
0.0003027882
0.0003021257
0.00030146496
0.00030080587
0.00030014824
0.00029949247
0.00029883825
0.00029818554
0.0002975347
0.00029688535
0.0002962376
0.00029559128
0.00029494686
0.00029430384
0.00029366268
0.00029302298
0.00029238482
0.00029174838
0.00029111333
0.00029048
0.0002898482
0.00028921783
0.0002885893
0.00028796226
0.0002873367
0.00028671257
0.0002860902
0.0002854693
0.00028485007
0.00028423214
0.00028361587
0.00028300128
0.00028238795
0.0002817763
0.00028116629
0.00028055767
0.0002799506
0.00027934497
0.0002787409
0.00027813826
0.00027753718
0.00027693756
0.00027633944
0.0002757429
0.0002751478
0.0002745541
0.00027396195
0.00027337112
0.0002727818
0.000272194
0.00027160766
0.0002710227
0.00027043928
0.00026985724
0.0002692766
0.0002686975
0.0002681197
0.0002675435
0.0002669686
0.0002663951
0.00026582298
0.00026525234
0.00026468313
0.00026411537
0.0002635489
0.0002629838
0.0002624203
0.00026185808
0.0002612972
0.00026073772
0.0002601796
0.00025962293
0.00025906775
0.00025851373
0.00025796134
0.0002574101
0.00025686063
0.0002563123
0.00025576542
0.0002552199
0.0002546758
0.00025413316
0.00025359183
0.00025305184
0.00025251356
0.00025197663
0.0002514412
0.0002509072
0.0002503747
0.0002498439
0.0002493144
0.00024878624
0.0002482595
0.00024773393
0.0002472097
0.00024668686
0.0002461653
0.0002456449
0.00024512594
0.00024460818
0.00024409182
0.00024357667
0.00024306269
0.0002425501
0.0002420387
0.00024152867
0.00024101992
0.00024051254
0.00024000625
0.00023950114
0.00023899757
0.00023849499
0.00023799369
0.00023749373
0.00023699485
0.0002364973
0.00023600094
0.00023550591
0.00023501206
0.00023451944
0.00023402808
0.00023353785
0.00023304888
0.00023256116
0.00023207456
0.00023158902
0.0002311048
0.00023062191
w is [0.101169]
b is [0.323778]每一次的运行结果不同
7.0669156e-12
w is [1.6494563]
b is [1.5937307]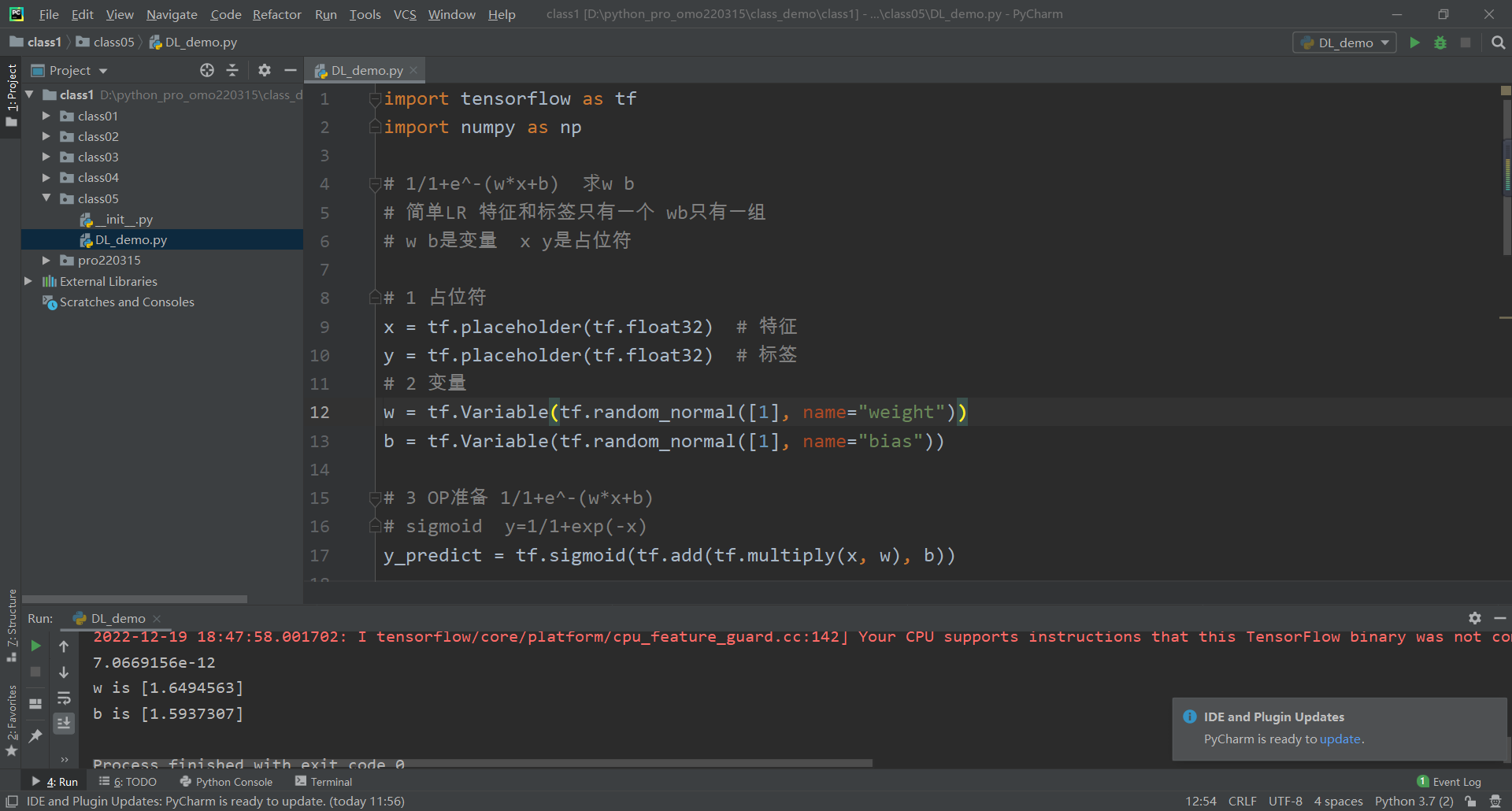
![[Java EE初阶]Thread 类的基本用法](https://img-blog.csdnimg.cn/196cfd101d1d49aba59c02956dd5e95a.png)