背包问题经典资料背包九讲,可以上网查一下相关资料。
下面的资料来自代码随想录和自己的一些个人理解,如有需要可以跳转代码随想录进行学习:代码随想录 (programmercarl.com)
背包一共分为01背包,完全背包,多重背包,分组背包,和混合背包,下图来自代码随想录
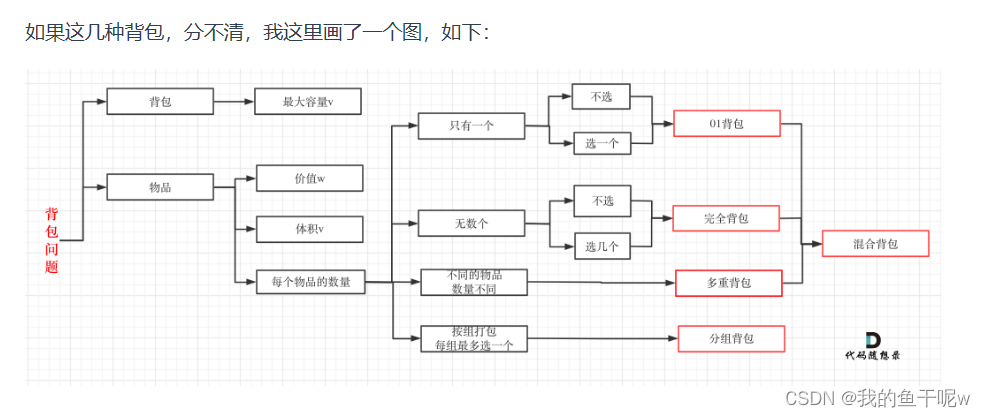
01背包是有n件物品和一个最多能背重量为w 的背包。且每件物品只能用一次,求解将哪些物品装入背包里物品价值总和最大。
根据动态规划的一般步骤来解决一下并给出01背包的模板:
1.确定dp数组以及下标的含义
定义dp[i][j] 表示从下标为[0-i]的物品里任意取,放进容量为j的背包,价值总和最大。
2.确定状态转移方程
对于每个物品,只有放或者不放两种可能,所以可得出:
不放:dp[i][j] = dp[i - 1][j]
放: dp[i][j] = dp[i - 1][j - weight[i]] + value[i]
3.初始化
从定义出发,容量j为0时,价值一定为0,即dp[i][0] = 0
再看状态转移方程,i是从i-1推导而来,所以要考虑i=0时,是可以选取第0号物品的,所以当j>weight[0]时将dp[0][j] = value[0]
4.确定遍历顺序
两种遍历顺序,先遍历物品或者先遍历容量,在01背包中可以,先遍历物品更好理解,需要注意一下的就是在完全背包中不同的遍历顺序的含义是不同的,后续再说吧。
5.举例推导验证一下
其次,背包问题的状态是可压缩的,我们可以将二维数组压缩成一维,对于递推公式:
dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i])
我们将dp[i-1]那一层拷贝到dp[i]这一层,就可以将递推公式改为:
dp[i][j] = max(dp[i][j], dp[i][j - weight[i]] + value[i])
这样就可以只用一维数组,即滚动数组,重复利用上一层的数据即可
1.确定dp数组以及下标的含义
定义dp[j] 表示容量为j的背包,所含物品的最大价值。
2.确定状态转移方程
对于每个物品,只有放或者不放两种可能,所以可得出:
不放:dp[j] = dp[j]
放: dp[j] = dp[j - weight[i]] + value[i]
3.初始化
从定义出发,容量j为0时,价值一定为0,即dp[0] = 0
4.确定遍历顺序
这里只能先遍历物品,然后再遍历背包容量,而且背包容量必须从大到小枚举,这样是为了保证每个物品只被放入一次。
思考一下,如果正序遍历,假设物品0重量weight[0] = 1,价值value[0] = 15,
dp[1] = dp[1 - weight[0]] + value[0] = 15
dp[2] = dp[2 - weight[0]] + value[0] = 30
可以发现物品0是被使用了两次,但是从逆序开始遍历,则是
dp[2] = dp[2 - weight[0]] + value[0] = 15
dp[1] = dp[1 - weight[0]] + value[0] = 15
因为倒序遍历能保证之前的状态是没有被使用的,而二维数组每次是由上一层推导来的,不会被同一层的状态影响
然后就是为什么只能先遍历物品呢?假如先遍历容量,假设有物品0 weight[0] = 1,价值value[0] = 5,物品1 weight[1] = 2,价值value[1] = 10,
可以发现第一次dp[3] = dp[3 - 1] + 5 = 5, 第二次dp[3] = dp[3 - 2] + 10 = 10,而前面的状态都是还没确定的,因为我们是逆序遍历容量,那么这样每个背包其实就只放入了一个物品,当然是错的。
5.举例推导验证一下
423. 采药 - AcWing题库
辰辰是个天资聪颖的孩子,他的梦想是成为世界上最伟大的医师。
为此,他想拜附近最有威望的医师为师。
医师为了判断他的资质,给他出了一个难题。
医师把他带到一个到处都是草药的山洞里对他说:“孩子,这个山洞里有一些不同的草药,采每一株都需要一些时间,每一株也有它自身的价值。我会给你一段时间,在这段时间里,你可以采到一些草药。如果你是一个聪明的孩子,你应该可以让采到的草药的总价值最大。”
如果你是辰辰,你能完成这个任务吗?
输入格式
输入文件的第一行有两个整数 T 和 M,用一个空格隔开,T 代表总共能够用来采药的时间,M 代表山洞里的草药的数目。
接下来的 M 行每行包括两个在 11 到 100100 之间(包括 11 和 100100)的整数,分别表示采摘某株草药的时间和这株草药的价值。
输出格式
输出文件包括一行,这一行只包含一个整数,表示在规定的时间内,可以采到的草药的最大总价值。
数据范围
1≤T≤1000,
1≤M≤100
输入样例:
70 3
71 100
69 1
1 2
输出样例:
3思路:典型的01背包问题,每个草药只能采一次,花费时间相当于所占容量,按套路来即可
#include <iostream> #include <cstring> #include <algorithm> using namespace std; const int N = 1010; int V, n; int v[N], w[N], dp[N]; int main() { scanf("%d%d", &V, &n); for(int i = 0; i < n; i ++ ) scanf("%d%d", &v[i], &w[i]); for(int i = 0; i < n; i ++ ) for(int j = V; j >= v[i]; j -- ) dp[j] = max(dp[j], dp[j - v[i]] + w[i]); printf("%d\n", dp[V]); return 0; }
1024. 装箱问题 - AcWing题库
1022. 宠物小精灵之收服 - AcWing题库
278. 数字组合 - AcWing题库