这篇文章我们来讲一下数据结构与算法中的二分查找
目录
1.介绍
1.1背景介绍
1.2算法介绍
2.实现
3.几个问题
4.算法改进
4.1左闭右开版
4.2 平衡版
4.3 Leftmost版
4.4 Leftmost返回 i 版
5.小结
1.介绍
首先,我们来介绍一下二分查找
1.1背景介绍
需求:在有序数组A内,现在需要查找目标值target,如果找到,返回目标值的索引,如果没找到,但会-1
二分查找就是为了解决这样的一个问题而产生的一种算法;
1.2算法介绍
下面来介绍一下算法。
二分查找有一个前提,即这必须是一个有序的数组(通常是升序的),即 A0<=A1<=A2<=……<=An,然后我们有一个待查找的目标值。之后,我们定义两个游标 i 与 j ,并且设置 i=0,j=n-1;即让 i 在最左边,j 在最右边。然后定义一个 m ,令 m = (i+j)/2 ,m要向下取整(也可以向上取整),此时 m 指向数组的中间位置。(注意:我们这里的 i 与 j 与 m 都是数据的索引值)我们将m所指的的值记为Am,然后,我们比较Am与目标值target进行比较,如果Am>target,说明Am右边的值都比target大,说明target比在Am左边,所以,我们令 j = m-1;然后比较 i 与 j;如果 i>j ,则说明找不到,就退出循环了,如果 i < j,则重复上述步骤,直到找到目标值或退出循环为止。
上述内容可以简化为下图:

2.实现
下面,我们来看一下具体的代码实现:

代码如下:
/**
* 二分查找基础版
*
* */
public class LC02 {
public static void main(String[] args) {
int[] a = {7,13,21,30,35,44,52,56,60};
int b = binarySearchBasic(a,31);
if (b>0)
System.out.println("找到了,索引为:"+b);
else
System.out.println("没找到");
}
public static int binarySearchBasic(int[] a,int target){
int i = 0; //定义头指针
int j = a.length-1; //定义尾指针
while (i<=j){ //进行循环的条件
int m = (i + j) >>> 1; //定义中间指针
if (target < a[m]){ //目标值与中间索引所指向的值进行比较
j = m-1; //移动指针
}else if (a[m] < target){
i = m+1;
}else{
return m; //返回目标索引
}
}
return -1; //没找到,返回-1
}
}
很简单,没啥好说的
3.几个问题
下面来探讨代码中的几个问题
问题1:上图的第18行,循环为什么要 while (i<=j) 而不能写成 while (i<j)?
答:写成 i<=j 表示当 i = j 时,也会进入循环进行判断,这就会把 i 和 j 索引所指向的值也包括的内,如果写成 i<j ,那么 i=j 时就不会进入循环,则会漏掉 i 与 j 所指向的值,就会出现错误情况。
问题2:上图的第19行,即求中间索引m的值,能不能写成 int m = (i + j) / 1,为什么?
答:不能。因为java中数值的表示是带符号位的,即最高位为0是正数,最高位为1是负数。如果写成 int m = (i + j) / 1 ,那么如果 i 与 j 的值过大时,会出现负数,这是一种错误的情况。具体的可以看下面的例子:
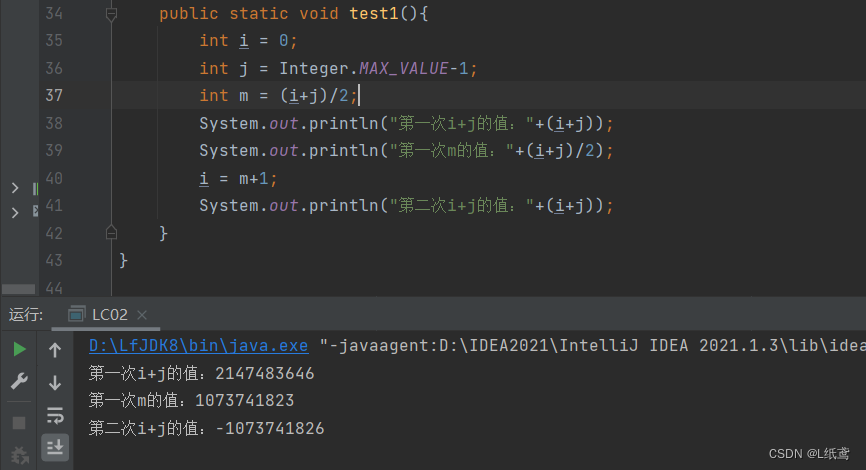
问题3:上图的第18,20,22行,那些条件判断为什么写的都是 < 号?
答:因为我们的数组是升序排列的,潜意识里面小的数在左边,大的数在右边,这样有利于我们的逻辑思考。当然这不是必须的。
4.算法改进
4.1左闭右开版
下面,我们来对这个算法改动一下:
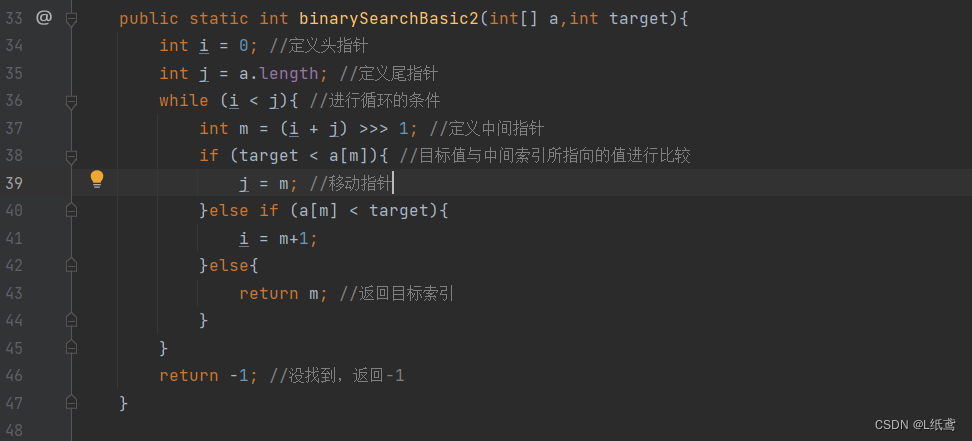
代码如下:
public static int binarySearchBasic2(int[] a,int target){
int i = 0; //定义头指针
int j = a.length; //定义尾指针
while (i < j){ //进行循环的条件
int m = (i + j) >>> 1; //定义中间指针
if (target < a[m]){ //目标值与中间索引所指向的值进行比较
j = m; //移动指针
}else if (a[m] < target){
i = m+1;
}else{
return m; //返回目标索引
}
}
return -1; //没找到,返回-1
}说明:
1. 第35行,j 由原来的 a.length-1,变为了 a.length ,这就表示 j 在一开始没有指向的元素,也就是说,后面 j 移动的时候,j 所指的元素就不再是目标元素,是目标元素之外的元素
2. 第36行,条件由 i<=j 变为了 i<j,这是因为如果写成 i<=j,那么当 i与 j 重合的时候,会陷入死循环,循环内会一直执行 j=m,这个自己带入数据自己演算一下就可以明白
3. 第39行,由原来的 j = m-1 变为了 j=m,这是因为 j 所指的元素一定不是目标元素,当目标值target小于m指向的元素时,就说明m指向的元素不是目标元素,此时要移动边界,那就直接让 j=m 就好。如果继续写 j = m-1 则会漏掉数组中的元素。
4. 这个只是换了一种写法,换个思路而已,性能方面是一样的,并不算是改进。
5. 注意:整个二分查找中,如果可以找到,最终指向目标值的一定是m
4.2 平衡版
下面来看一下二分查找的平衡版
首先,我们就着基础版的代码来讨论一个问题
假设,我们确定了要循环L次,如果目标元素在最左边,请问循环内部的判断要判断多少次?答:判断L次,只需要第一次判断就可以了;如果目标元素在最右边,请问循环内部的判断要判断多少次?答:2L次,因为第一次的判断要执行L次,第二次的判断也要执行L次,所以是2L次。
这就是一种不平衡的情况,那么请问如何进行平衡的二分查找?
请看下面的代码:
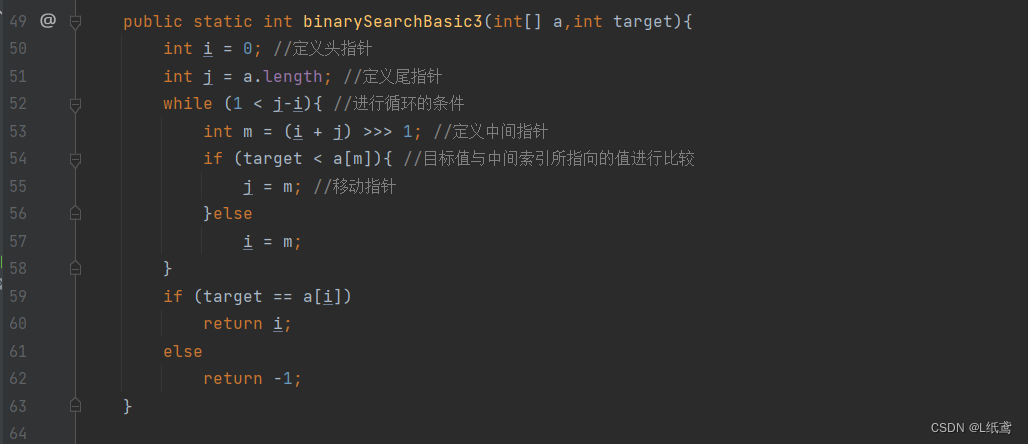
代码如下:
public static int binarySearchBasic3(int[] a,int target){
int i = 0; //定义头指针
int j = a.length; //定义尾指针
while (1 < j-i){ //进行循环的条件
int m = (i + j) >>> 1; //定义中间指针
if (target < a[m]){ //目标值与中间索引所指向的值进行比较
j = m; //移动指针
}else
i = m;
}
if (target == a[i])
return i;
else
return -1;
}下面讲一下思路:
不平衡的原因是多了一重else if。如果没有这重else if,即根据某个条件比较,如果符合,就移动某个边界,不符合移动另一个边界,这样就可以做到平衡了。我们根据这个思路来看一下代码。
还是一样,首先定义两个边界,这里的 j 依然指向无效值。然后看循环,1< j-i 意思是说当 i 与 j 中间还有1个或更多元素的时候,进行循环,然后依然是找中点,然后将中点指向的值与目标值进行比较,如果目标值小,那么就让 j = m,如果目标值大于或等于中点索引所指向的值,那么就让 i = m ,最后,当 i 与 j 相邻的时候,即 j -i =1 的时候,退出循环。最后,我们来看一下索引 i 指向的值,如果等于目标值,那么就返回 i ,如果不等于,就是没找到,返回-1。这里要说明一下,在循环的过程中,其实是一个逐渐缩小范围逼进的过程,因为最开始的定,j是一定不可能指向有效元素的,所以最终指向目标值的只能是 i ,这就是最终只用再比较一下 i 指向的值就能返回值的原因,其实这一点也是二分查找的核心思想,就是一个缩小范围,逐渐逼近的过程。(注意:整个二分查找中,如果可以找到,最终指向目标值的一定是m)
平衡版的二分查找与基础版的二分查找相比,它的时间复杂度稳定在O(),而基础版的二分查找的时间复杂度为O(n),其最好的情况是O(1)即目标值刚好在中间,最坏是O(2n)即在右边时。所以,总体来说,平衡版的二分查找要优于基础版的二分查找。
4.3 Leftmost版
下面来思考这样一个问题,如果一个数组中有重复的目标元素,我们应该如何做才能让返回的是最左边的目标元素?
思路1:当我们找到目标元素时,即m指向目标元素时,我们继续移动 i 与 j ,此时 i =m-1,然后比较 i 指向的值与目标元素,如果相等,再移动 i ,直到不相等为止(这只是一个思路,代码实现很复杂,并且如果 i 指向的值不等于目标值的话,无法返回m的索引)
思路2:在1的思路上我们改进一下,我们可以先用一个值来记录m的索引,将找到的m作为一个候选值。既然m找到了,并且我们要找的是最左边的元素,并且这是一个升序有序的数组,所以,我们只需要移动 j 就行,让 j=m-1 ,这样缩小范围后继续进行二分查找,如果找到了,那么就更新记录m的值的值,如果没找到,那么就返回一开始记录m值的值(这才是正确的思路)
下面来看一下代码实现:
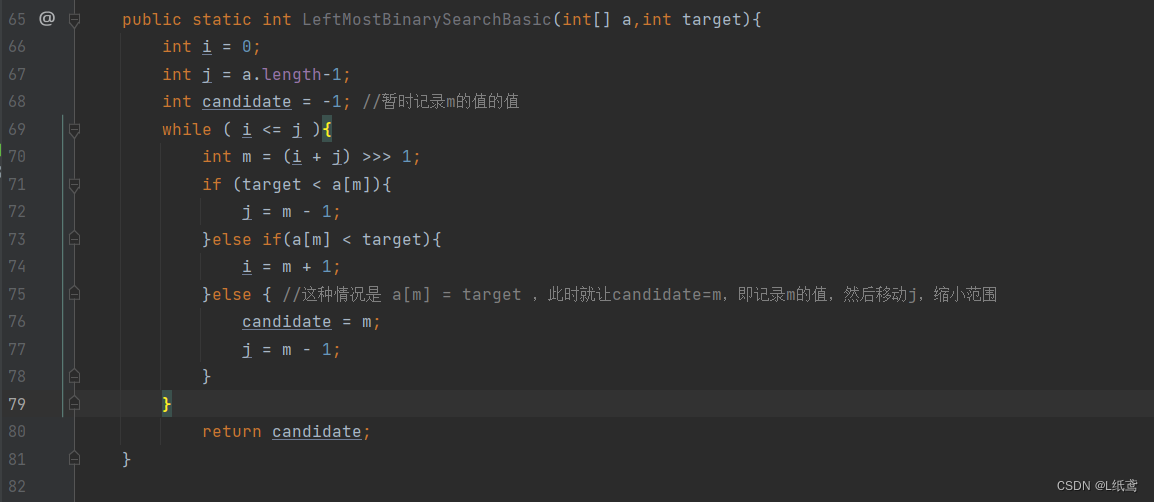
具体代码:
public static int LeftMostBinarySearchBasic(int[] a,int target){
int i = 0;
int j = a.length-1;
int candidate = -1; //暂时记录m的值的值
while ( i <= j ){
int m = (i + j) >>> 1;
if (target < a[m]){
j = m - 1;
}else if(a[m] < target){
i = m + 1;
}else { //这种情况是 a[m] = target ,此时就让candidate=m,即记录m的值,然后移动j,缩小范围
candidate = m;
j = m - 1;
}
}
return candidate;
}当然,如果查找最右边的目标元素的思路和这一样,只需要让 j=m-1 变为 i=m+1 就行
4.4 Leftmost返回 i 版
前面我们已经讲了二分查找的Leftmost版,但是当没找到时,我们返回的是-1,这个-1属于无效值,那么我们是否可以让其返回一个有效的有意义的值?可以的,我们可以来看一下下面的代码;
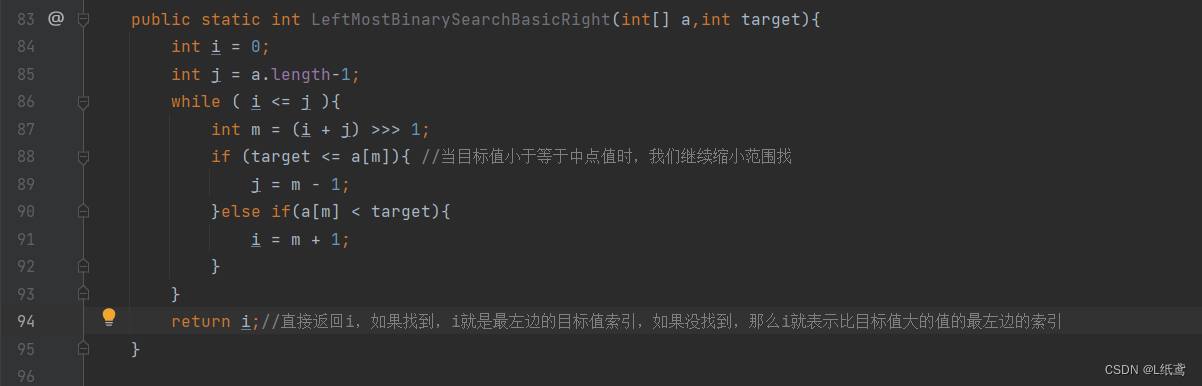
代码如下:
public static int LeftMostBinarySearchBasicRight(int[] a,int target){
int i = 0;
int j = a.length-1;
while ( i <= j ){
int m = (i + j) >>> 1;
if (target <= a[m]){ //当目标值小于等于中点值时,我们继续缩小范围找
j = m - 1;
}else if(a[m] < target){
i = m + 1;
}
}
return i;//直接返回i,如果找到,i就是最左边的目标值索引,如果没找到,那么i就表示比目标值大的值的最左边的索引
}返回 j 的意义和代码与上面相似,这里就不写了
除此之外,力扣的第34,35,704题都是二分查找的题目,有兴趣的可以去看一下。
5.小结
其实二分查找就是一个缩小范围,逐渐逼近的过程,在查找的过程中,最终能够指向目标元素的一定是m,如果 i 指向,m的值也会等于 i 值,所以最终指向目标元素的一定是m,i 与 j 只起圈范围的作用。写代码的时候,我们一定要清楚,i 与 j 不同的取值,最终查找结束的时候它们会停留在哪里?是目标值处?还是目标值的相邻处?这个要清楚。最后,就是要清楚二分查找的时间复杂度。