卡尔曼滤波应用到交通领域
- 滤波器介绍
- 核心思想
- 核心公式
- 一维卡尔曼滤波器示例
- 导入所需的库
滤波器介绍
卡尔曼滤波器是一种用于估计系统状态的数学方法,它以卡尔曼核心思想为基础,广泛应用于估计动态系统的状态和滤除测量中的噪声。以下是卡尔曼滤波器的核心思想和介绍:
-
系统状态估计: 卡尔曼滤波器的主要目标是估计动态系统的状态,这个状态通常由一个多维向量表示,包含了系统在不同方面的参数。例如,可以用卡尔曼滤波器来估计飞机的位置、速度和方向,或者用来估计汽车的位置和速度等。
-
状态转移模型: 卡尔曼滤波器使用状态转移模型来描述系统状态如何随时间变化。这个模型通常表示为一个线性系统方程,它将当前时刻的状态与前一个时刻的状态以及系统的控制输入关联起来。状态转移模型描述了系统的动态行为。
-
测量模型: 卡尔曼滤波器还使用测量模型来描述如何从传感器或测量中获得观测数据。测量模型通常也是线性的,它将系统状态映射到观测数据的空间。测量模型告诉滤波器如何将系统状态与观测数据关联起来。
-
预测步骤: 卡尔曼滤波器的核心思想之一是预测步骤,它用于根据系统的状态转移模型预测下一个时刻的状态。在这一步骤中,滤波器估计系统的状态将如何变化,但尚未考虑测量数据。
-
更新步骤: 更新步骤是卡尔曼滤波器的另一个核心思想。在此步骤中,滤波器考虑到实际的测量数据,根据测量模型和当前的状态预测来更新状态估计。这个步骤通过融合测量数据和预测来改善状态估计的精确度。
-
连续迭代: 卡尔曼滤波器是一个递归滤波器,意味着它可以连续地迭代进行状态估计。在每个时间步中,滤波器都会进行预测和更新,从而不断改进对系统状态的估计。
-
高斯分布假设: 卡尔曼滤波器通常基于高斯分布假设,即系统的状态和测量噪声都服从高斯分布。这个假设使得卡尔曼滤波器在数学上更容易处理,但也限制了其适用性。
卡尔曼滤波器广泛应用于诸如导航、机器人控制、金融建模、信号处理等领域。它在处理具有不确定性和噪声的动态系统时非常有用,可以提供对系统状态的精确估计。然而,要成功应用卡尔曼滤波器,需要精确地建立状态转移模型和测量模型,并且要了解系统的特性和噪声。
核心思想
卡尔曼滤波的核心思想是通过融合两个来源的信息来估计动态系统的状态:1) 来自系统的先验信息(基于过去状态的预测),和 2) 来自传感器或测量的信息。它通过不断迭代的方式,通过预测和更新步骤来提高对系统状态的估计精度。
具体来说,卡尔曼滤波的核心思想可以概括为以下几点:
状态估计的不确定性管理: 卡尔曼滤波器维护对系统状态的估计以及估计的不确定性。状态估计通常表示为一个多维向量,而状态的不确定性则通过状态协方差矩阵来表示。
状态转移模型: 卡尔曼滤波器使用系统的状态转移模型来预测下一个时刻的状态。这个模型描述了系统状态如何随时间变化。
测量模型: 卡尔曼滤波器使用测量模型来将实际测量数据映射到状态空间。测量模型描述了如何从传感器或测量中获得观测数据。
预测步骤: 在预测步骤中,滤波器使用状态转移模型来预测下一个时刻的状态,但不考虑测量数据。这一步骤提供了先验估计和估计的不确定性。
更新步骤: 在更新步骤中,滤波器使用测量数据来校正先验估计,从而改善状态估计的精度。这一步骤考虑了测量模型和观测数据的不确定性。
连续迭代: 卡尔曼滤波器是递归的,可以连续迭代进行状态估计,每个时间步都进行预测和更新,不断提高状态估计的精度。
总之,卡尔曼滤波的核心思想是在状态估计中同时考虑先验信息和测量信息,通过动态系统模型和测量模型的融合来估计系统的状态,并随着时间的推移不断改进估计的精度。这使得卡尔曼滤波器在处理具有不确定性和噪声的动态系统时非常有效。
核心公式
状态向量 (State Vector): 表示系统的状态,通常用 x 表示。状态向量可以是多维的,包括系统在不同方面的参数。在时刻 k,状态向量表示为 x(k)。
状态协方差矩阵 (State Covariance Matrix): 表示状态估计的不确定性,通常用 P 表示。它描述了每个状态参数的方差和协方差。在时刻 k,状态协方差矩阵表示为 P(k)。
系统动态方程 (State Transition Equation): 描述状态如何随时间变化,通常表示为状态转移矩阵 A 和控制输入向量 B(如果适用)。系统动态方程可以表示为以下公式:
x(k+1) = A * x(k) + B * u(k) + w(k)
其中,x(k) 表示时刻 k 的状态向量,u(k) 表示时刻 k 的控制输入向量(如果适用),w(k) 表示过程噪声。
观测矩阵 (Observation Matrix): 描述如何从测量中获得观测数据,通常表示为 H。观测矩阵将状态向量映射到观测数据的空间。观测方程可以表示为以下公式:
z(k) = H * x(k) + v(k)
其中,z(k) 表示时刻 k 的观测数据,v(k) 表示观测噪声。
观测噪声协方差矩阵 (Observation Noise Covariance Matrix): 描述观测数据的噪声性质,通常表示为 R。它表示观测数据中的方差和协方差。
这些公式构成了卡尔曼滤波的核心数学表述。滤波器的工作包括在每个时间步进行以下两个主要步骤:
**预测步骤 (**Prediction Step): 根据系统动态方程进行状态预测,同时更新状态协方差矩阵以反映预测的不确定性。
更新步骤 (Update Step): 利用观测数据来更新状态估计,根据观测矩阵和观测噪声协方差矩阵来计算新的状态估计和状态协方差矩阵。
卡尔曼滤波的目标是通过这两个步骤连续迭代,不断提高对系统状态的估计精度。这些数学公式和步骤构成了卡尔曼滤波算法的核心,用于处理具有不确定性和噪声的动态系统。
一维卡尔曼滤波器示例
本示例演示了一维卡尔曼滤波器的基本实现步骤。
导入所需的库
import numpy as np
import matplotlib.pyplot as plt
在此示例中,我们导入了NumPy用于数值计算和Matplotlib用于绘图。
定义卡尔曼滤波器参数
A = 1 # 状态转移矩阵
H = 1 # 观测矩阵
Q = 0.01 # 状态噪声的协方差
R = 0.1 # 观测噪声的协方差
x_hat = 0 # 初始状态估计
P = 1 # 初始估计误差的协方差
这些参数用于定义卡尔曼滤波器的模型。A是状态转移矩阵,H是观测矩阵,Q和R是状态噪声和观测噪声的协方差,x_hat是初始状态估计,P是初始估计误差的协方差。
生成模拟数据
true_values = np.linspace(0, 10, 100)
measurements = true_values + np.random.normal(0, np.sqrt(R), 100)
在此示例中,我们生成了一个包含100个数据点的"真实值"和带有观测噪声的测量值。
初始化滤波器
filtered_values = []
我们初始化一个空列表来存储卡尔曼滤波器估计的状态值。
迭代处理测量值
for z in measurements:
我们遍历测量值列表。
预测步骤
x_hat_minus = A * x_hat
P_minus = A * P * A + Q
在每个时间步骤中,我们执行预测步骤。首先,我们使用状态转移矩阵A估计下一个状态(x_hat_minus),然后更新估计误差的协方差(P_minus)。
更新步骤
K = P_minus * H / (H * P_minus * H + R)
x_hat = x_hat_minus + K * (z - H * x_hat_minus)
P = (1 - K * H) * P_minus
在更新步骤中,我们计算卡尔曼增益K,然后使用测量值来更新状态估计(x_hat)和估计误差的协方差(P)。
存储估计值
filtered_values.append(x_hat)
我们将每个时间步骤的估计状态值存储在filtered_values列表中。
绘制结果
plt.figure(figsize=(12, 6))
plt.plot(true_values, label='True Values', color='b')
plt.plot(measurements, label='Measurements', color='g', alpha=0.5)
plt.plot(filtered_values, label='Filtered Values', color='r')
plt.legend()
plt.title('Kalman Filter Demo')
plt.xlabel('Time Steps')
plt.ylabel('Value')
plt.show()
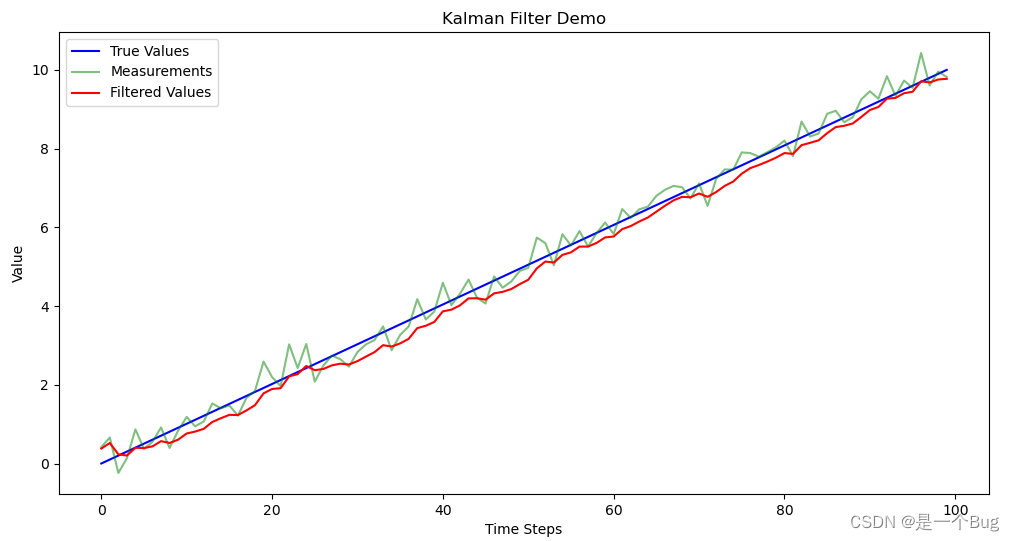
最后,我们使用Matplotlib绘制了"真实值"、测量值和卡尔曼滤波器估计的值的图表,以可视化卡尔曼滤波的效果。
这就是一维卡尔曼滤波器的基本实现步骤。卡尔曼滤波器的关键在于预测和更新步骤,其中卡尔曼增益(K)用于融合测量值和状态估计,从而提供更准确的状态估计。在实际应用中,卡尔曼滤波器可以用于传感器数据融合、目标跟踪等各种应用中。