"议论平恕,无所向背”
- 1. 位姿图
- 1.1 具体做法
- 1.2 小结
- 2. 因子图
- 2.1 具体做法
- 2.1.1 贝叶斯网络
- 2.1.2 因子图
- 2.1.3 更具体的因子图
- 2.1.4 增量的求解方法
引入:
- 上节BA将位姿和路标都作为优化的节点,H矩阵也告诉我们路标远大于位姿,时长会导致资源等问题。
办法:
- 滑动窗口法:保持H固定大小,丢弃历史
- 位姿图:不管路标,只管位姿,从BA变成Pose Graph,容易看出资源会少很多很多,如下:
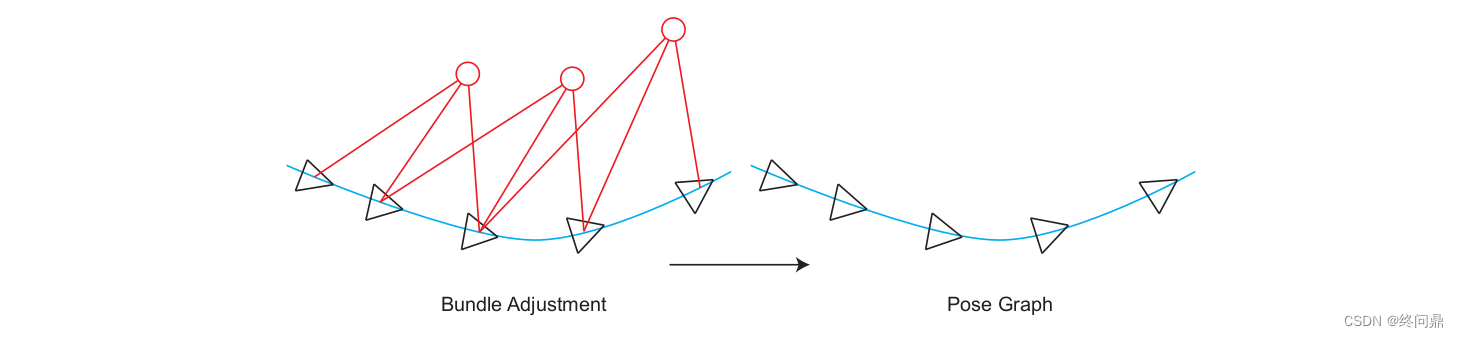
1. 位姿图
1.1 具体做法
其实仍然是用构建非线性最小二乘问题然后优化解的,只是优化变量变成了位姿 ξ \xi ξ 。
- 假设,位姿 ξ i \xi_i ξi 经过运动 Δ ξ i j \Delta \xi_{ij} Δξij 变到了 ξ j \xi_j ξj ,根据李群李代数知识,有如下等式:
Δ ξ i j = ξ i − 1 ∘ ξ j = l n ( e x p ( − ξ i ) ^ e x p ( ξ j ^ ) ) ˇ \Delta \xi_{ij} = \xi_i^{-1} \circ \xi_j = ln(exp(-\xi_i)\hat{} \; exp(\xi_j \hat{})) \v{} Δξij=ξi−1∘ξj=ln(exp(−ξi)^exp(ξj^))ˇ
用李群表示则如下:
Δ T i j = T i − 1 T j \Delta T_{ij} = T_i^{-1} T_j ΔTij=Ti−1Tj
将
T
i
j
T_{ij}
Tij 右移:
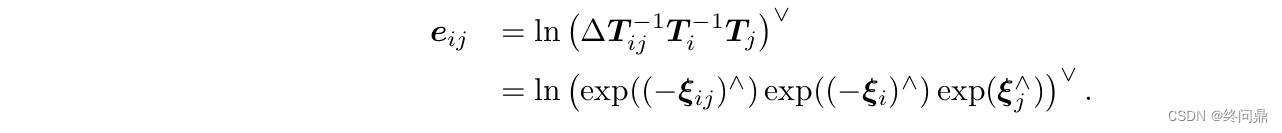
求它关于优化变量
ξ
i
\xi_i
ξi 和
ξ
j
\xi_j
ξj 的导数,按照李群李代数的方法,中间过程略,最终构建的总体目标函数如下:
min ξ 1 2 ∑ i , j ∈ ε e i j T Σ i j − 1 e i j \min\limits_{\xi} \frac{1}{2} \sum\limits_{i,j \in \varepsilon} e_{ij}^T \Sigma^{-1}_{ij}e_{ij} ξmin21i,j∈ε∑eijTΣij−1eij
这里的 ε \varepsilon ε 就是所有边的集合,二范数含义就是平方项。关于这个问题的求解,我们可以用G-N,L-M等之前用的很多。略。
1.2 小结
自从PTAM提出来以后,后端优化没必要实时性了;人们将前后端分开作两个线程–跟踪和建图。
前段需要实时响应视频速度,如每秒30HZ,而后端优化只要完成后将结果返回给前端即可,所以实时性没必要了。
2. 因子图
2.1 具体做法
在介绍因子图的做法前,要先了解贝叶斯网络。
2.1.1 贝叶斯网络
直接用一个动态的贝叶斯网络来表达我们的SLAM的运动和观测方程:
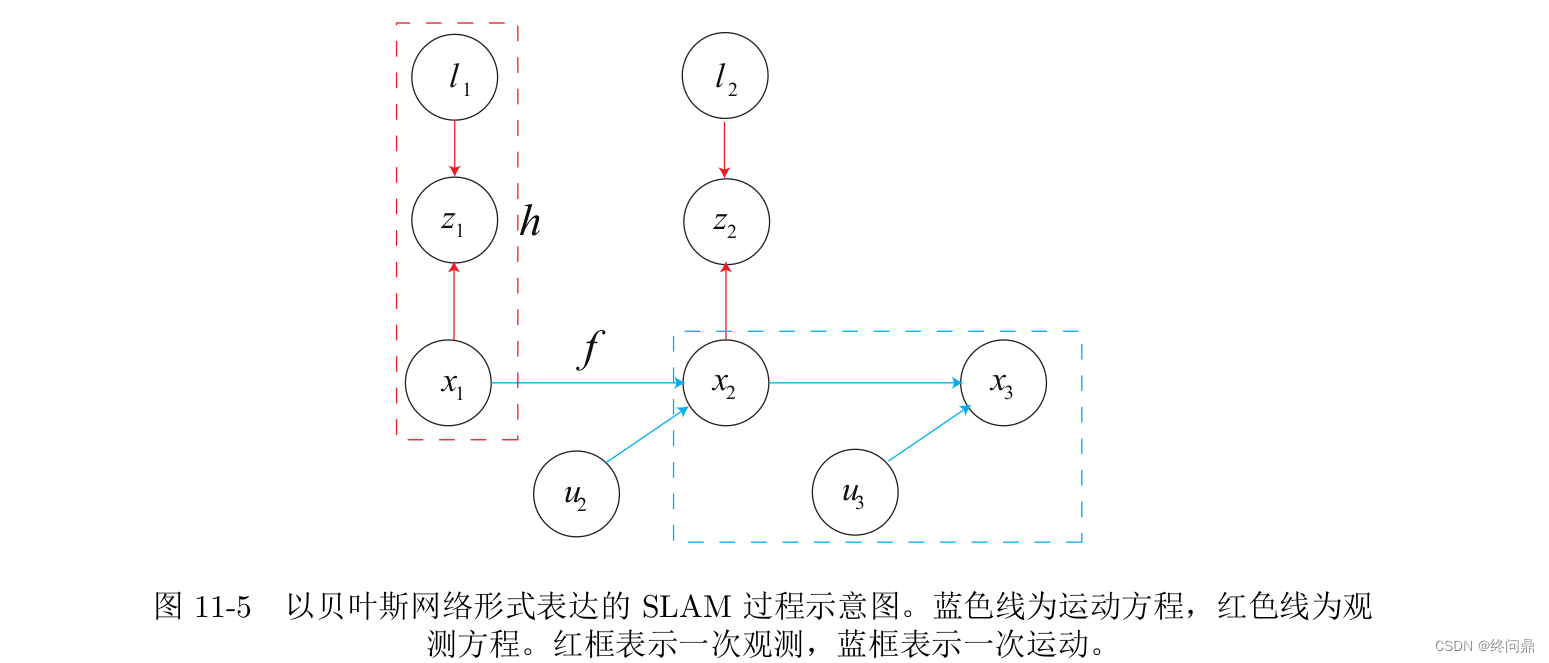
- x x x 表示位姿节点
- u u u 输入量节点
- l l l 路标节点
- z z z 观测数据节点
- 箭头表示依赖关系,比如 x 2 x_2 x2 在运动方程中就依赖于 u 2 u_2 u2 和 x 1 x_1 x1, 图中也是这么标注的。
- 一次观测或者一次运动实际上是给出的条件概率关系:
P ( x 3 ∣ x 2 , u 3 ) P ( z 1 ∣ x 1 , l 1 ) P(x_3|x_2, u_3) \qquad\quad P(z_1|x_1,l_1) P(x3∣x2,u3)P(z1∣x1,l1)
图绘制完,我们后端优化的目标就是—不断调整贝叶斯网络中随机变量的取值,使得整个网络的后验概率最大化:
{ x , l } ∗ = a r g m a x ( x 0 ) ∏ P ( x k ∣ x k − 1 , u k ) ∏ P ( z k ∣ x i , l j ) \{x,l\}^* = arg max(x_0) \prod P(x_k|x_{k-1}, u_k) \prod P(z_k|x_i, l_j) {x,l}∗=argmax(x0)∏P(xk∣xk−1,uk)∏P(zk∣xi,lj)
我们发现要做这个公式,里边的乘积会很多,所以将因子化为节点,会更直观,就得到了—因子图
2.1.2 因子图
根据上边的公式,可以重新结合公式和概率公式绘制网络,得到因子图:
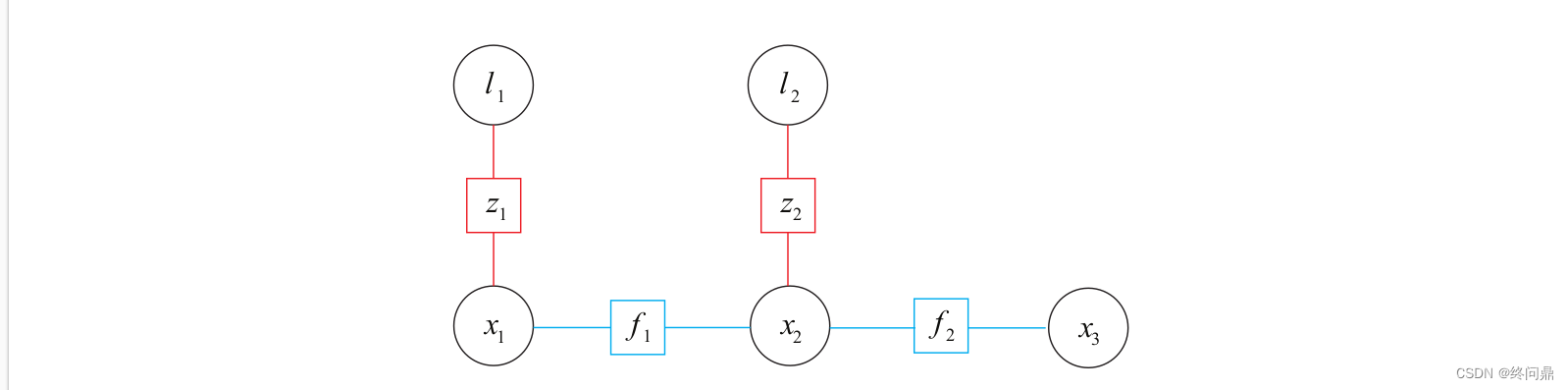
- 圆圈: 变量节点
- 方块: 因子节点
此时要解决因子乘积最大化的问题,通常,取所有因子的条件概率为高斯分布的形式,则运动数据和观测数据符合:
P ( x k ∣ x k − 1 ) = N ( f ( x k − 1 , u k ) , R k ) P ( z k j ∣ x k , l j ) = N ( h ( x k , l j ) , Q k j ) P(x_k|x_{k-1}) = N(f(x_{k-1}, u_k), R_k)\qquad P(z_{kj}|x_k, l_j) = N(h(x_k, l_j), Q_{kj}) P(xk∣xk−1)=N(f(xk−1,uk),Rk)P(zkj∣xk,lj)=N(h(xk,lj),Qkj)
同样的,它的解法—因子图优化,和之前的类似,也是用GN,LM等。
2.1.3 更具体的因子图
在实际中,我们可能不止有相机,还有其他先验信息—比如,GPS等,它们测到的点是确定的,也就是这些点的先验信息知道了,就可以在图中添加它们的先验信息了,还有编码器,IMU等。如下:
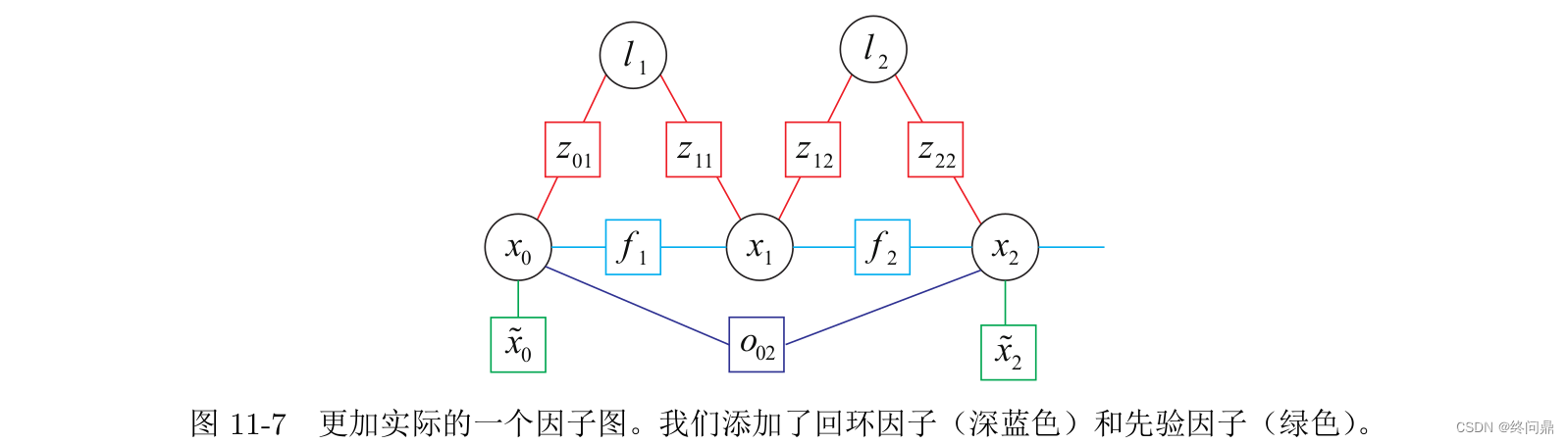
2.1.4 增量的求解方法
无论怎么求,最后都会落到这一步:
H Δ x = g H \Delta x = g HΔx=g
但是,当新的节点和新的边加入,它的所有节点更新量就要重新计算一次更新量。
对资源占用很大。我们继续分析因子图:
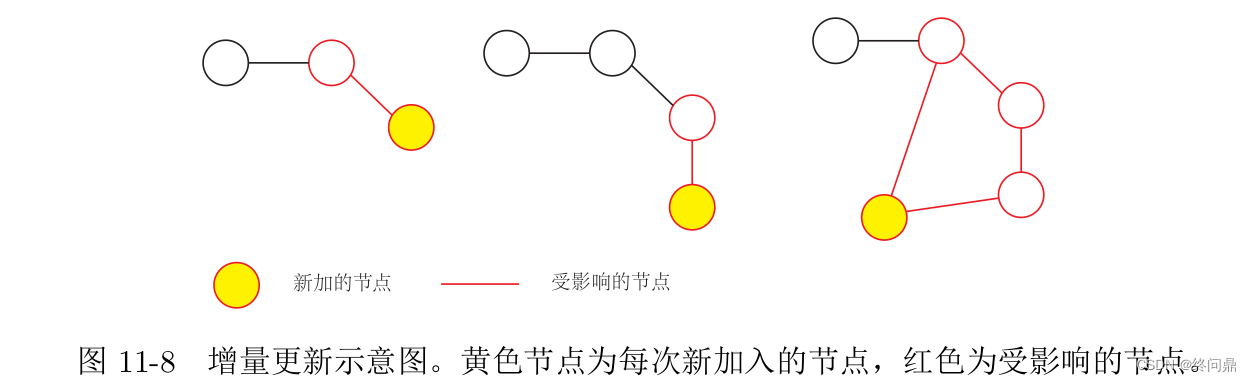
- 按照里程计的方式添加节点,在因子图中只有最后一个与之相连的节点会受影响。(实际上是接近的影响大一点)
- 那么我们只需要在有新的变量和因子加入时,分析它和因子图的连接和影响关系:
-
-
- 如果按照回环检测方式添加,回环开始到这一帧这一段的节点都受影响,都要调整
-
-
-
- 如果只添加一个任意节点,则影响区域几乎只作用于离他最近的点
-
如下: