这个系列是实战(刘二大人讲的pytorch)
建议把代码copy下来放在编译器查看(因为很多备注在注释里面)
线性模型(Linear Model):
import numpy as npimport matplotlib.pyplot as plt #绘图的包x_data = [1.0, 2.0, 3.0] #这两行代表数据集,一般x_data,y_data是要把它分开保存的,x表示输入样本y_data = [2.0, 4.0, 6.0] #相同的索引表示一组样本,就是(1.0,2.0)表示一对样本,(2.0,4.0)表示一对样本。def forward(x): #定义模型,取名“前馈模型”return x * w #用x与w相乘返回(Linear Model)def loss(x, y): #定义损失函数y_pred = forward(x)return (y_pred - y) ** 2# 穷举法w_list = [] #权重值mse_list = [] #对应权重损失值for w in np.arange(0.0, 4.1, 0.1): #权重间隔为0.1,从0.0开始取,4.0结束。[0.0,0.1,...,4.0]print("w=", w)l_sum = 0for x_val, y_val in zip(x_data, y_data): #把x_data,y_data这两个列表里边的数据拿出来用zip拼成真实数据的x,y值y_pred_val = forward(x_val) #首先计算预测(可以不计算,主要只是打印一下结果看一下);y_pred_val是预测值,loss函数计算会用到loss_val = loss(x_val, y_val) #计算损失l_sum += loss_val #损失求和print('\t', x_val, y_val, y_pred_val, loss_val)print('MSE=', l_sum / 3)w_list.append(w)mse_list.append(l_sum / 3) #除以3,转成mse(均方误差)plt.plot(w_list, mse_list) #绘图plt.ylabel('Loss')plt.xlabel('w')plt.show()

使用到的损失函数如下:
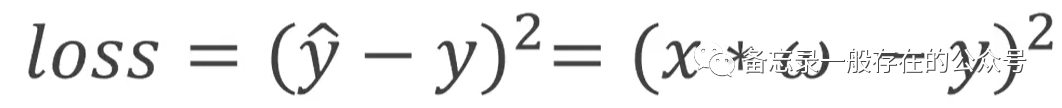
"y_pred"就是在求

zip函数:

【番外:可视化常用到的工具---visdom】
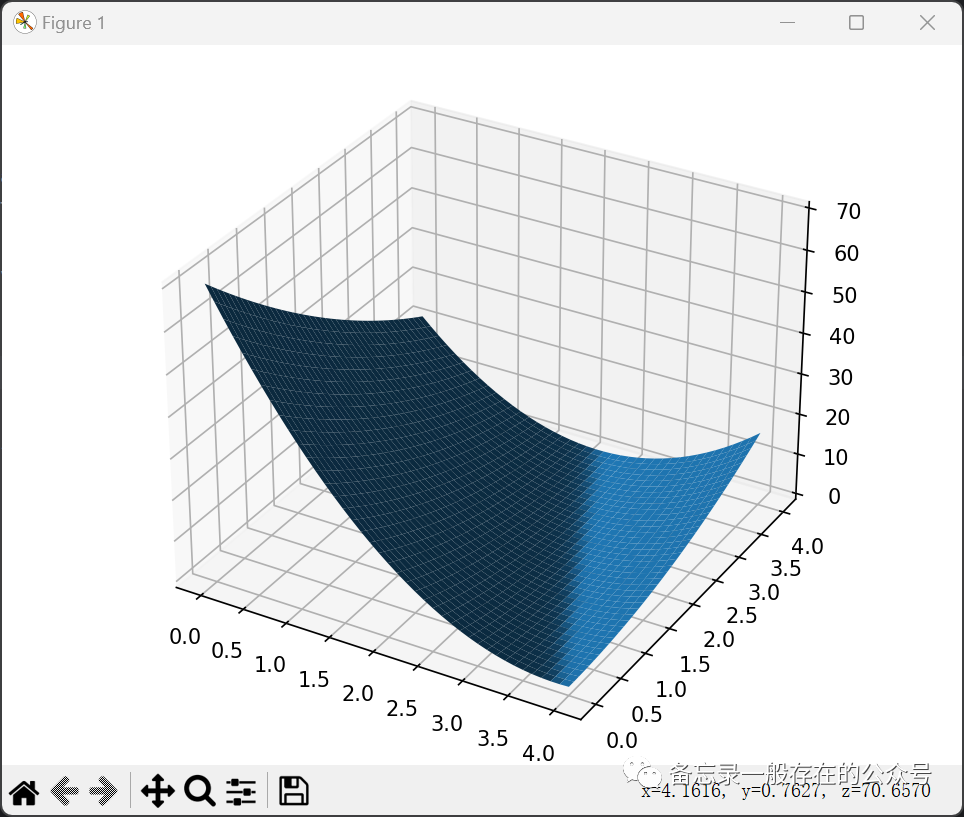
练习:实现线性模型(y=wx+b)并输出loss的3D图像。
import numpy as npimport matplotlib.pyplot as pltfrom mpl_toolkits.mplot3d import Axes3D#这里设函数为y=3x+2x_data = [1.0,2.0,3.0]y_data = [5.0,8.0,11.0]def forward(x):return x * w + bdef loss(x,y):y_pred = forward(x)return (y_pred-y)*(y_pred-y)mse_list = []W=np.arange(0.0,4.1,0.1)B=np.arange(0.0,4.1,0.1)[w,b]=np.meshgrid(W,B)l_sum = 0for x_val, y_val in zip(x_data, y_data):y_pred_val = forward(x_val)print(y_pred_val)loss_val = loss(x_val, y_val)l_sum += loss_valfig = plt.figure()ax = Axes3D(fig)fig.add_axes(ax)ax.plot_surface(w, b, l_sum/3)plt.show(block=True)
梯度下降
(鞍点:梯度为0。陷入鞍点没办法迭代)

cost公式:(cost function是对所有的样本)

代码:
import matplotlib.pyplot as plt# 准备训练集数据x_data = [1.0, 2.0, 3.0] #两个列表,分别表示x和y的值,(1.0,2.0)表示第一条数据样本y_data = [2.0, 4.0, 6.0] #(2.0,4.0)表示第二条数据样本# initial guess of weightw = 1.0 #初始权重猜测# define the model linear model y = w*xdef forward(x): #定义前馈计算return x * w #y^# define the cost function MSEdef cost(xs, ys): #把所有的数据都拿进来cost = 0for x, y in zip(xs, ys):y_pred = forward(x) #算y^cost += (y_pred - y) ** 2return cost / len(xs) #MSE(平均损失的计算)# define the gradient function gddef gradient(xs, ys): #求梯度grad = 0for x, y in zip(xs, ys):grad += 2 * x * (x * w - y)return grad / len(xs)epoch_list = []cost_list = []print('predict (before training)', 4, forward(4))for epoch in range(100): #训练过程(100轮)cost_val = cost(x_data, y_data) #计算当前损失值,也就是costgrad_val = gradient(x_data, y_data) #求梯度w -= 0.01 * grad_val # 0.01 learning rate #学习率*梯度print('epoch:', epoch, 'w=', w, 'loss=', cost_val)epoch_list.append(epoch)cost_list.append(cost_val)print('predict (after training)', 4, forward(4))plt.plot(epoch_list, cost_list)plt.ylabel('cost')plt.xlabel('epoch')plt.show()
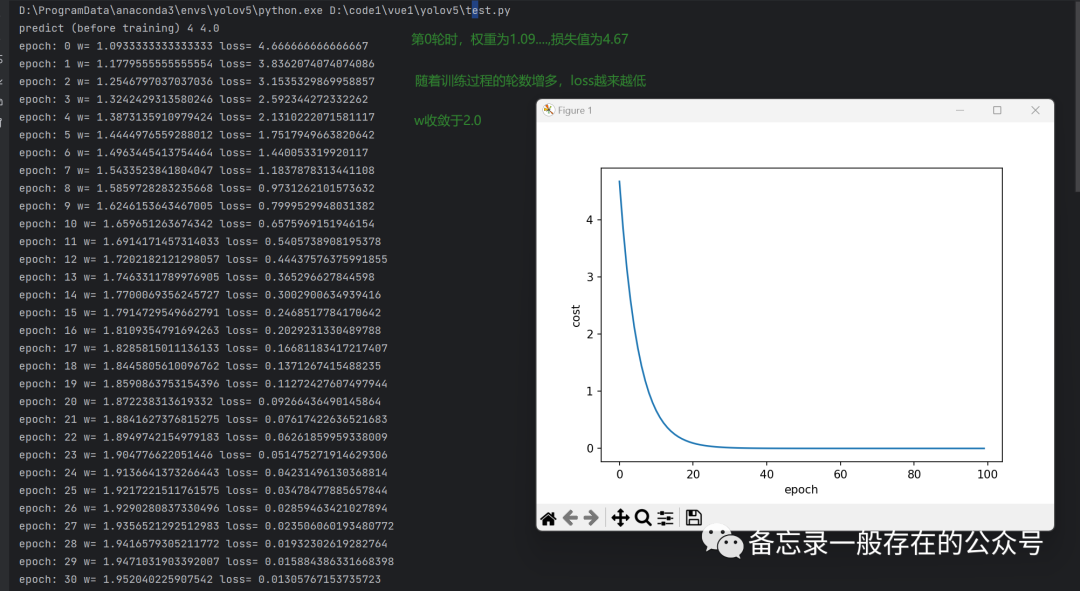

【番外:“指数加权均值”方法能够将cost变得更平滑】
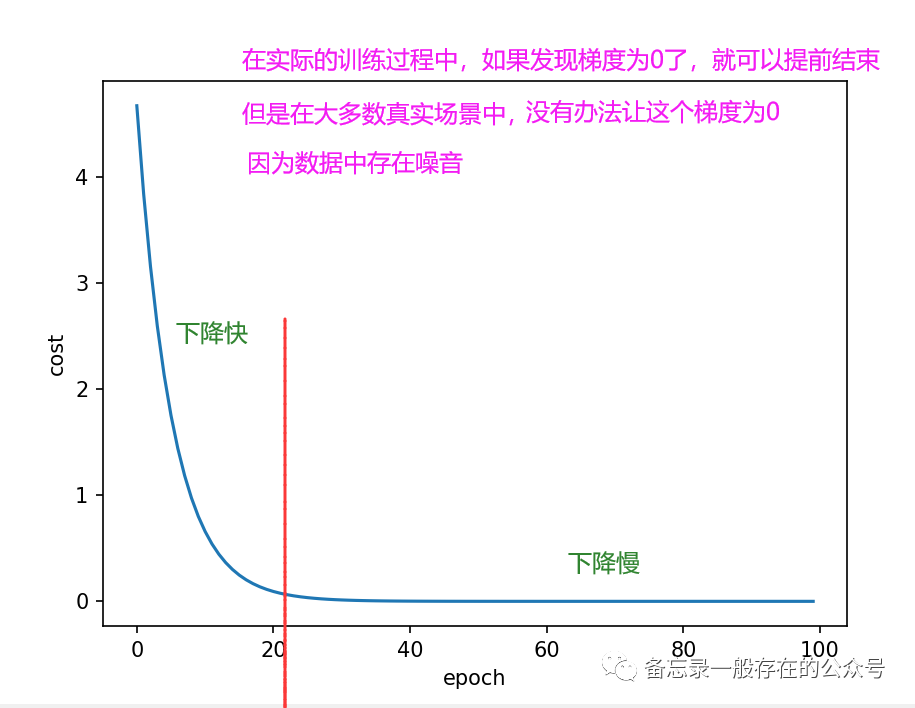
在大多数的情况下,得到的loss图像形状趋势都是如上图所示,如果出现右边有又上去了的情况,则说明训练发散了,这次训练失败了。
训练失败的情况有很多,其中最常见的是:学习率取得太大。(可以将学习率调小再看看效果)
随机梯度下降
(只用一个样本,即使陷入了鞍点,也也有可能跨过这个鞍点向前推进找最优点)
公式:(单个样本的损失函数对权重求导,然后进行更新)


代码:
import matplotlib.pyplot as pltx_data = [1.0, 2.0, 3.0]y_data = [2.0, 4.0, 6.0]w = 1.0def forward(x):return x * w# calculate loss functiondef loss(x, y):y_pred = forward(x) #y^return (y_pred - y) ** 2 #loss# define the gradient function sgddef gradient(x, y):return 2 * x * (x * w - y) #梯度epoch_list = []loss_list = []print('predict (before training)', 4, forward(4))for epoch in range(100):for x, y in zip(x_data, y_data):grad = gradient(x, y) #对每一个样本求梯度,loss对w求梯度w = w - 0.01 * grad # update weight by every grad of sample of training set 更新print("\tgrad:", x, y, grad)l = loss(x, y) #计算现在的损失print("progress:", epoch, "w=", w, "loss=", l)epoch_list.append(epoch)loss_list.append(l)print('predict (after training)', 4, forward(4))plt.plot(epoch_list, loss_list)plt.ylabel('loss')plt.xlabel('epoch')plt.show()
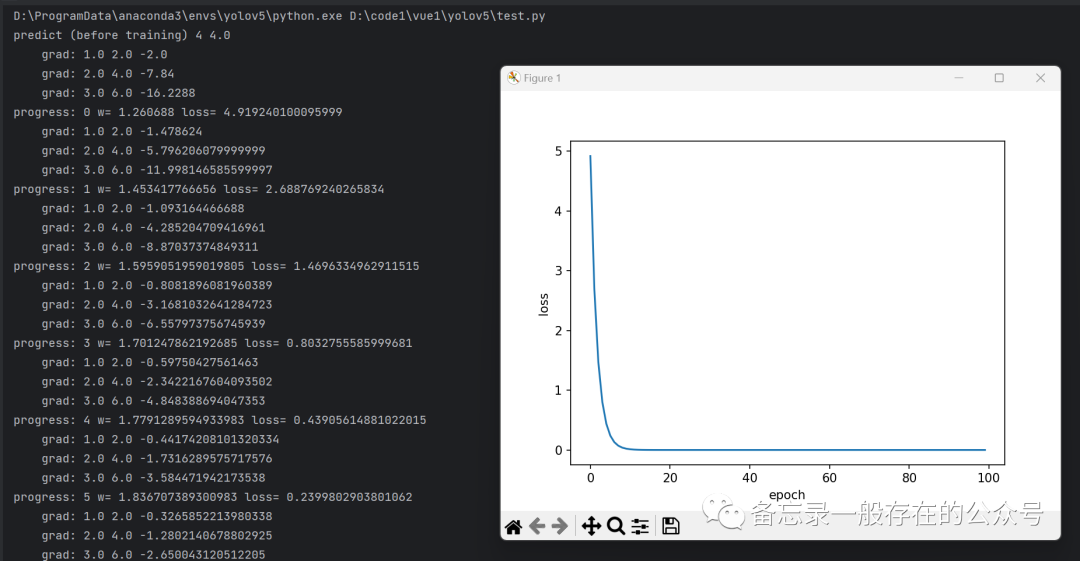
性能好,但时间复杂度太高,没有并行性。
【番外:Batch。(性能和时间复杂度上取折中)批量的随机梯度下降法。
就是说如果你全都丢到一起,性能不好;全都分开呢,时间复杂度不好。
因此可以若干个分为一组,每次用这一租样本去求相应的梯度,然后进行更新。这个就叫做Batch。】