本文属于「征服LeetCode」系列文章之一，这一系列正式开始于2021/08/12。由于LeetCode上部分题目有锁，本系列将至少持续到刷完所有无锁题之日为止；由于LeetCode还在不断地创建新题，本系列的终止日期可能是永远。在这一系列刷题文章中，我不仅会讲解多种解题思路及其优化，还会用多种编程语言实现题解，涉及到通用解法时更将归纳总结出相应的算法模板。

为了方便在PC上运行调试、分享代码文件，我还建立了相关的仓库：https://github.com/memcpy0/LeetCode-Conquest。在这一仓库中，你不仅可以看到LeetCode原题链接、题解代码、题解文章链接、同类题目归纳、通用解法总结等，还可以看到原题出现频率和相关企业等重要信息。如果有其他优选题解，还可以一同分享给他人。

由于本系列文章的内容随时可能发生更新变动，欢迎关注和收藏征服LeetCode系列文章目录一文以作备忘。

在一个 8x8 的棋盘上，放置着若干「黑皇后」和一个「白国王」。

给定一个由整数坐标组成的数组 queens ，表示黑皇后的位置；以及一对坐标 king ，表示白国王的位置，返回所有可以攻击国王的皇后的坐标(任意顺序)。

示例 1：

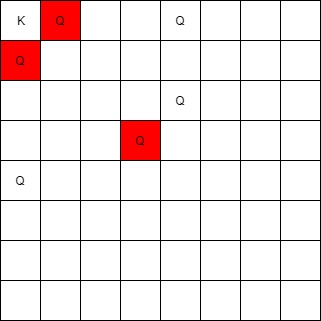
输入：queens = [[0,1],[1,0],[4,0],[0,4],[3,3],[2,4]], king = [0,0]
输出：[[0,1],[1,0],[3,3]]
解释：
[0,1] 的皇后可以攻击到国王，因为他们在同一行上。 
[1,0] 的皇后可以攻击到国王，因为他们在同一列上。 
[3,3] 的皇后可以攻击到国王，因为他们在同一条对角线上。 
[0,4] 的皇后无法攻击到国王，因为她被位于 [0,1] 的皇后挡住了。 
[4,0] 的皇后无法攻击到国王，因为她被位于 [1,0] 的皇后挡住了。 
[2,4] 的皇后无法攻击到国王，因为她和国王不在同一行/列/对角线上。

示例 2：

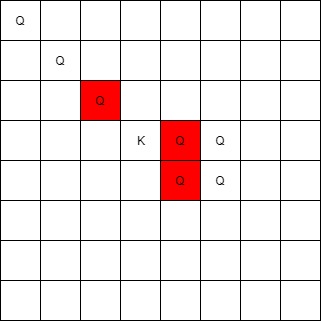
输入：queens = [[0,0],[1,1],[2,2],[3,4],[3,5],[4,4],[4,5]], king = [3,3]
输出：[[2,2],[3,4],[4,4]]

示例 3：

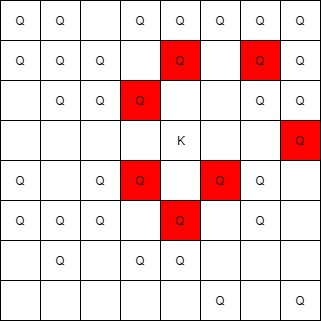
输入：queens = [[5,6],[7,7],[2,1],[0,7],[1,6],[5,1],[3,7],[0,3],[4,0],[1,2],[6,3],[5,0],[0,4],[2,2],[1,1],[6,4],[5,4],[0,0],[2,6],[4,5],[5,2],[1,4],[7,5],[2,3],[0,5],[4,2],[1,0],[2,7],[0,1],[4,6],[6,1],[0,6],[4,3],[1,7]], king = [3,4]
输出：[[2,3],[1,4],[1,6],[3,7],[4,3],[5,4],[4,5]]

提示：

• 1 <= queens.length <= 63
• queens[i].length == 2
• 0 <= queens[i][j] < 8
• king.length == 2
• 0 <= king[0], king[1] < 8
• 一个棋盘格上最多只能放置一枚棋子。

---

解法 数组+模拟

能攻击到国王的皇后，需要满足：

• 皇后与国王在同一行，或者同一列，或者同一斜线。
• 皇后与国王之间没有棋子。换句话说，皇后不能被其它皇后挡住。

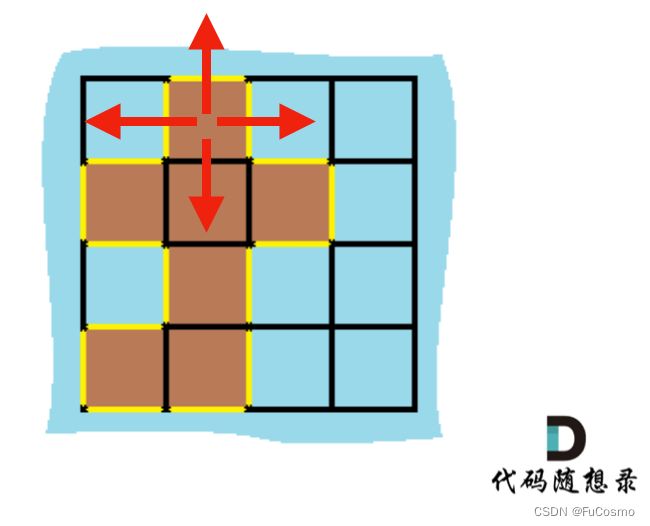
一种思路是枚举每个皇后，去判断是否满足上述条件。更加巧妙的做法是，站在国王的视角，计算有哪些皇后能被国王「看到」。想象成从国王的位置发射八个方向的射线，记录每条射线首次遇到的皇后。

class Solution {
    const int directions[8][2] = {{1, 0}, {1, 1}, {0, 1}, {-1, 1}, {-1, 0}, {-1, -1}, {0, -1}, {1, -1}};
public:
    vector<vector<int>> queensAttacktheKing(vector<vector<int>> &queens, vector<int> &king) {
        bool is_queen[8][8]{}; // 数组效率比哈希表高
        for (auto &q: queens) is_queen[q[0]][q[1]] = true;
        vector<vector<int>> ans;
        for (auto &d: directions) {
            int x = king[0] + d[0];
            int y = king[1] + d[1];
            while (0 <= x && x < 8 && 0 <= y && y < 8) {
                if (is_queen[x][y]) {
                    ans.push_back({x, y});
                    break;
                }
                x += d[0];
                y += d[1];
            }
        }
        return ans;
    }
};

复杂度分析：

• 时间复杂度：$\mathcal{O}(m+n)$ 。其中 $m$ 为 $\text{queens}$ 的长度，$n=8$ 为棋盘边长。
• 空间复杂度：$\mathcal{O}(m)$ 。