编程获取图像中的圆半径

news2024/10/5 23:51:22

即将推出EmguCV的教程，请大家还稍作等待。

之前网友咨询如何获得图像中圆形的半径，其中有两个十字作为标定，十字之间距离为100mm。如下图：

说实在的，单靠VB.net很难获得相关圆形信息，为了弥补这部分知识，下定决心学习了EmguCV。以下是具体代码：https://blog.csdn.net/UruseiBest

        Dim msrc As New Mat("C:\learnEmgucv\celiang.jpg", ImreadModes.Color)

        Dim mgray As New Mat()
        CvInvoke.CvtColor(msrc, mgray, ColorConversion.Bgr2Gray)

        Dim kernel As New Mat
        kernel = CvInvoke.GetStructuringElement(ElementShape.Cross, New Drawing.Size(3, 3), New Point(-1, -1))

        Dim merode As New Mat        '
        '这里使用了2次迭代
        CvInvoke.Dilate(mgray, merode, kernel, New Point(-1, -1), 1, BorderType.Constant, Nothing)

        CvInvoke.Threshold(merode, merode, 200, 255, ThresholdType.BinaryInv)


        '获得所有轮廓 https://blog.csdn.net/UruseiBest
        Dim contours As New VectorOfVectorOfPoint
        Dim hierarchy As New VectorOfRect

        CvInvoke.FindContours(merode, contours, hierarchy, RetrType.List, ChainApproxMethod.ChainApproxSimple)
        Dim m2 As New Mat(merode.Size, DepthType.Cv8U, 1)
        m2.SetTo(New MCvScalar(0))


        '圆轮廓
        Dim contourCircle As VectorOfPoint

        '圆轮廓的周长
        Dim perimeter As Double

        '绘制轮廓 https://blog.csdn.net/UruseiBest
        For i As Integer = 0 To contours.Size - 1
            Dim carea As VectorOfPoint = contours(i)
            '获得轮廓面积
            Dim area As Double = CvInvoke.ContourArea(carea, False)
            '符合条件时，绘制轮廓，排除圆形，只保留十字线 
            '本图中圆形面积为2449，直线面积为8，需要根据实际情况调整
            If area < 200 Then
                CvInvoke.DrawContours(m2, contours, i, New MCvScalar(255), 0.4)
            Else
                '得到圆形，图像中只有三个轮廓：2个交叉十字线段、1个圆形
                '这里简化操作，否则在多个轮廓情况下，应获取最大面积的轮廓判断为圆形
                contourCircle = contours(i)

                '获取轮廓周长
                perimeter = CvInvoke.ArcLength(contourCircle, True)
            End If
        Next
        ImageBox1.Image = m2

        '使用HoughLinesP方法检测图像中的直线，并将其绘制到图像
        '因为本图中十字线上的线段较短，所以这里阈值设置很小
        Dim lines As LineSegment2D() = CvInvoke.HoughLinesP(m2, 1, Math.PI / 180, 5, 5, 80)

        Dim m3 As New Mat(merode.Size, DepthType.Cv8U, 3)
        m3.SetTo(New MCvScalar(0, 0, 0))

        For Each line As LineSegment2D In lines
            CvInvoke.Line(m3, line.P1, line.P2, New MCvScalar(0, 255, 0), 2)
        Next

        ImageBox2.Image = m3

       '对直线进行分类，将其分为垂直和水平两类：
        Dim verticalLines As New List(Of LineSegment2D)
        Dim horizontalLines As New List(Of LineSegment2D)

        '计算每条直线的倾斜角度来进行分类，
        '将倾斜角度在60 - 120度之间的直线划分为垂直类，
        '将倾斜角度在30 - 150度之间的直线划分为水平类。
        For Each line As LineSegment2D In lines
            Dim angle As Double = Math.Atan2(line.P2.Y - line.P1.Y, line.P2.X - line.P1.X) * 180 / Math.PI
            If angle < 0 Then angle += 180

            If angle > 60 AndAlso angle < 120 Then
                verticalLines.Add(line)
            ElseIf angle > 150 OrElse angle < 30 Then
                horizontalLines.Add(line)
            End If
        Next

        '对垂直和水平直线进行匹配，并计算十字中心点的位置：
        Dim intersections As New List(Of PointF)

        '得到两个相交点 https://blog.csdn.net/UruseiBest
        For Each verticalLine As LineSegment2D In verticalLines
            For Each horizontalLine As LineSegment2D In horizontalLines
                '基于图像中两条直线真实相交，
                '如果垂直线的中点X坐标在水平线两端点X坐标之间
                '那么，这条垂直线段和这条水平线段相交
                Dim centerX As Single = (verticalLine.P1.X + verticalLine.P2.X) / 2
                If horizontalLine.P1.X < horizontalLine.P2.X Then
                    If centerX > horizontalLine.P1.X And centerX < horizontalLine.P2.X Then
                        Dim intersectionPoint As New PointF(
                            (horizontalLine.P1.X + horizontalLine.P2.X + verticalLine.P1.X + verticalLine.P2.X) / 4,
                            (horizontalLine.P1.Y + horizontalLine.P2.Y + verticalLine.P1.Y + verticalLine.P2.Y) / 4
                        )
                        intersections.Add(intersectionPoint)
                    End If
                Else
                    If centerX > horizontalLine.P2.X And centerX < horizontalLine.P1.X Then
                        Dim intersectionPoint As New PointF(
                            (horizontalLine.P1.X + horizontalLine.P2.X + verticalLine.P1.X + verticalLine.P2.X) / 4,
                            (horizontalLine.P1.Y + horizontalLine.P2.Y + verticalLine.P1.Y + verticalLine.P2.Y) / 4
                        )
                        intersections.Add(intersectionPoint)
                    End If
                End If
            Next
        Next

        If intersections.Count <> 2 Then
            MessageBox.Show("未能获得两个十字线的交叉点")
            Exit Sub
        End If
        CvInvoke.Line(msrc, PointFToPoint(intersections(0)), PointFToPoint(intersections(1)), New MCvScalar(0, 255, 0), 2)

        CvInvoke.Imshow("m3", msrc)

       '计算两个交点的距离
        Dim distance As Double = Math.Sqrt(
            (intersections(0).X - intersections(1).X) ^ 2 +
            (intersections(0).Y - intersections(1).Y) ^ 2
        )

        '实际中两交点距离为100毫米，计算相应比例
        Dim proportion As Double = 100 / distance


        '以下是基于最小外接圆来计算实际圆半径
        Dim cf As CircleF
        cf = CvInvoke.MinEnclosingCircle(contourCircle)
        '获得外接圆形 https://blog.csdn.net/UruseiBest
        CvInvoke.Circle(msrc, New Point(CInt(cf.Center.X), CInt(cf.Center.Y)), cf.Radius, New MCvScalar(0, 0, 255), 2)
        CvInvoke.Imshow("m4", msrc)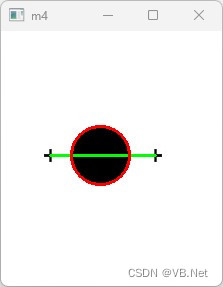

       '实际圆半径
        Dim realradius1 As Double
        realradius1 = proportion * cf.Radius


        '以下是基于轮廓周长来计算实际圆半径
        '实际圆周长
        Dim realperimeter As Double = perimeter * proportion

        '图像中的圆半径 https://blog.csdn.net/UruseiBest
        Dim radius As Double
        radius = (perimeter / Math.PI) / 2

        '实际圆半径
        Dim realradius2 As Double
        realradius2 = proportion * radius

        MessageBox.Show("最小外接圆来计算实际圆半径：" & realradius1 & ControlChars.CrLf &
                        "基于轮廓周长来计算实际圆半径：" & realradius2)