快速掌握差分以及差分矩阵

前言

之前我们提到了前缀和数组与前缀和矩阵，现在我们可以类比处差分矩阵，差分数组
，现在我将站在新手的角度为大家介绍，学完差分的小伙伴们也可以复习一下

差分

差分的定义【官方解释】

差分是指在数学中，对于一个数列或函数，通过计算相邻元素之间的差值来得到一个新的数列或函数。差分可以用来描述数列或函数的变化趋势或规律。

对于一个数列 {a1, a2, a3, ..., an}，它的一阶差分可以表示为 {d1, d2, d3, ..., dn-1}，其中 di = ai+1 - ai。

对于一个函数 f(x)，它的一阶差分可以表示为 f'(x) = f(x+1) - f(x)。

差分可以应用于各种数学领域，如微积分、离散数学、动态规划等。它在数值计算和数据分析中也有广泛的应用，可以用来处理时间序列数据、图像处理、信号处理等问题。

差分自定义【跟前缀和放在一起理解】

对于一个数组{a1, a2, a3, ..., an}，我们可以有前缀和s[N],
s[1]=a[1];
s[2]=a[2]+a[1]
s[3]=a[3]+a[2]+a[1]
............
类比对于一个数组{a1, a2, a3, ..., an}
我们有
b[1]=a[1]-a[0]
b[2]=b[2]-b[1]
b[3]=b[3]-b[2]
................
我们叫{b1, b2, b3, ..., bn}是{a1, a2, a3, ..., an}的差分数组；

差分数组的应用

对差分数组的前缀和数组进行范围修改；
a[1]=b[1];
a[2]=b[1]+b[2]
a[3]=b[1]+b[2]+b[3]
........................
数组a[N]就是b[N]的前缀和数组，假设我们要对a[N],进行修改，在【l,r】的范围内加上 w，假如直接对数组 a [ N ] 进行遍历操作，那么我们的时间复杂度是 O(N);

但是我们现在有了差分数组，我们就不用对 a [N ]做直接修改了，我们从它的差分数组入手，对 b[left] 进行修改，那么 a[ i ] ,a [ i+1 ] ,a [ i+2 ], a [ i+3] …就会发生改变，但是我们不能让改变一直延续下去，所以要在 b [ right ]处进行修改 【及时进行相反的操作,这样就实现了范围修改

题目描述

输入一个长度为 n 的整数序列。

接下来输入 m个操作，每个操作包含三个整数 l,r,c，表示将序列中 [l,r]
之间的每个数加上 c

请你输出进行完所有操作后的序列。

输入格式第一行包含两个整数 n 和 m

第二行包含 n 个整数，表示整数序列。

接下来 m 行，每行包含三个整数 l，r，c，表示一个操作。

输出格式
共一行，包含 n 个整数，表示最终序列。

数据范围
1≤n,m≤100000
1≤l≤r≤n
−1000≤c≤1000
−1000≤整数序列中元素的值≤1000
输入样例：
6 3
1 2 2 1 2 1
1 3 1
3 5 1
1 6 1
输出样例：
3 4 5 3 4 2
`

#include<iostream>
using namespace std;
const int N =1e5 +7;
int a[N],b[N];
int n,m;
int main(){
    cin>>n>>m;
    for(int i=1;i<=n;i++){
        //由于是前缀和，下标要从 1 开始
        cin>>a[i];
        b[i]=a[i]-a[i-1];
    }
    while(m--){
        int l,r,c;
        cin>>l>>r>>c;
        b[l]+=c,b[r+1]-=c;
        //此处不要忘记进行相反的操作
    }
    for(int i=1;i<=n;i++){
        a[i]=b[i]+a[i-1];//重新构建前缀和
        cout<<a[i]<<' ';
    }
}

差分矩阵【与前缀和矩阵进行比较】

有关前缀和矩阵的知识请看我的另2篇博客
激光矩阵问题: https://blog.csdn.net/2302_77698668/article/details/132345058

前缀和求解k倍区间问题: https://blog.csdn.net/2302_77698668/article/details/132339559

差分矩阵定义【官方解释】

差分矩阵是指由差分操作得到的矩阵。在离散数学和图论中，差分矩阵常用于描述图的性质和图算法的设计。

对于一个无向图 G = (V, E)，其中 V 是顶点集合，E 是边集合。差分矩阵 D 是一个 |V| × |V| 的矩阵，其中 |V| 表示顶点的个数。差分矩阵的定义如下：

D(i, j) = -1, if i ≠ j and (i, j) ∈ E,
degree(i), if i = j,
0, otherwise.

其中，D(i, j) 表示差分矩阵的第 i 行第 j 列的元素，degree(i) 表示顶点 i 的度数（即与顶点 i 相连的边的个数）。

差分矩阵可以用来描述图的拉普拉斯矩阵，它是一个对称半正定矩阵，具有很多重要的性质和应用。差分矩阵在图论算法中也有广泛的应用，如最短路径算法、最小生成树算法、图分割算法等。

自定义

跟之前一样，我们继续类比推理
a [i] [j] 是 矩阵【 b[1] [1](左上端点)，b[i][j] 右下端点】的和
那么要对 a [ i ] [ j ]进行范围修改，我们就只需要对 b[N][N]进行修改

修改操作【跟前缀和对比】

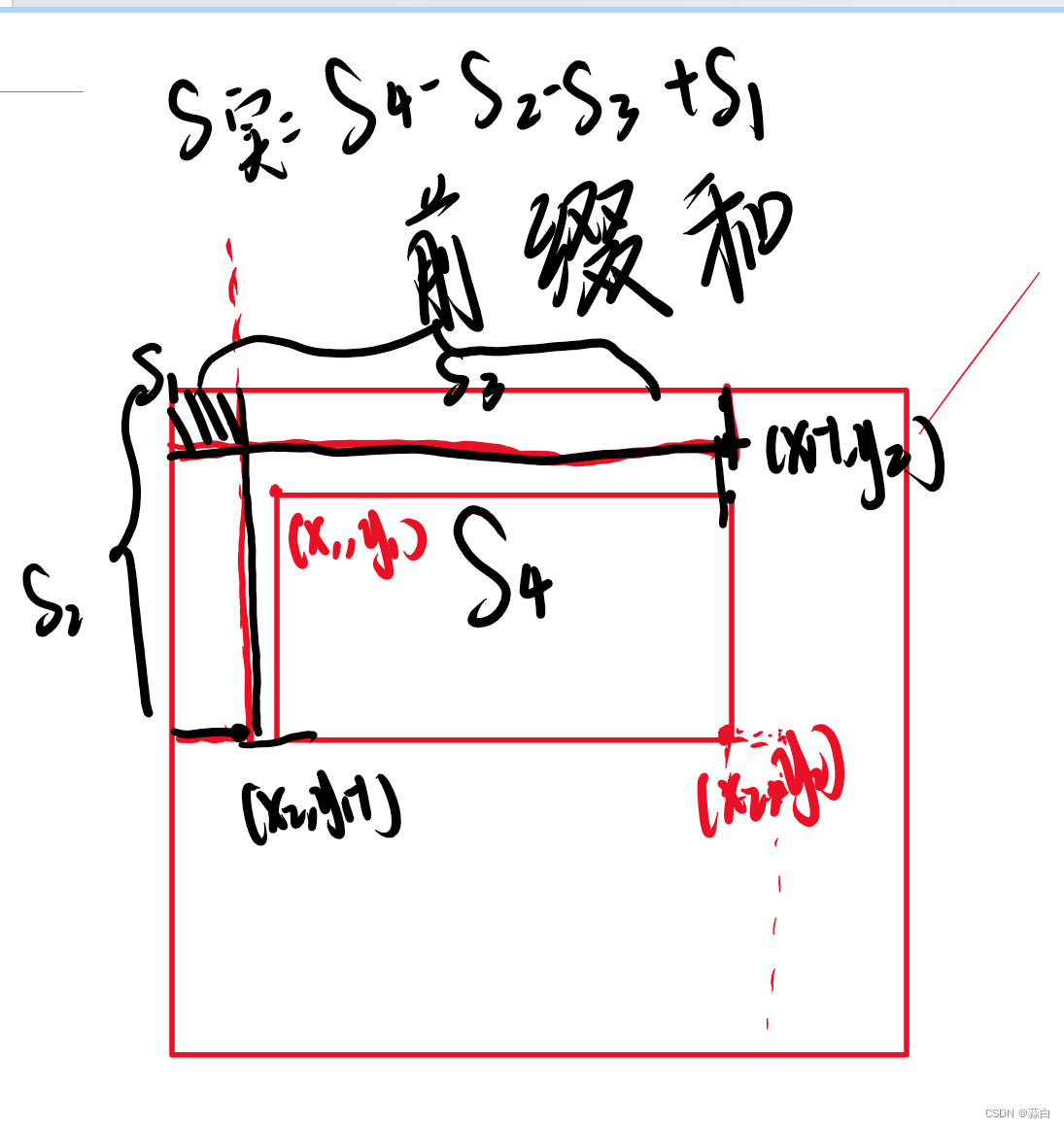
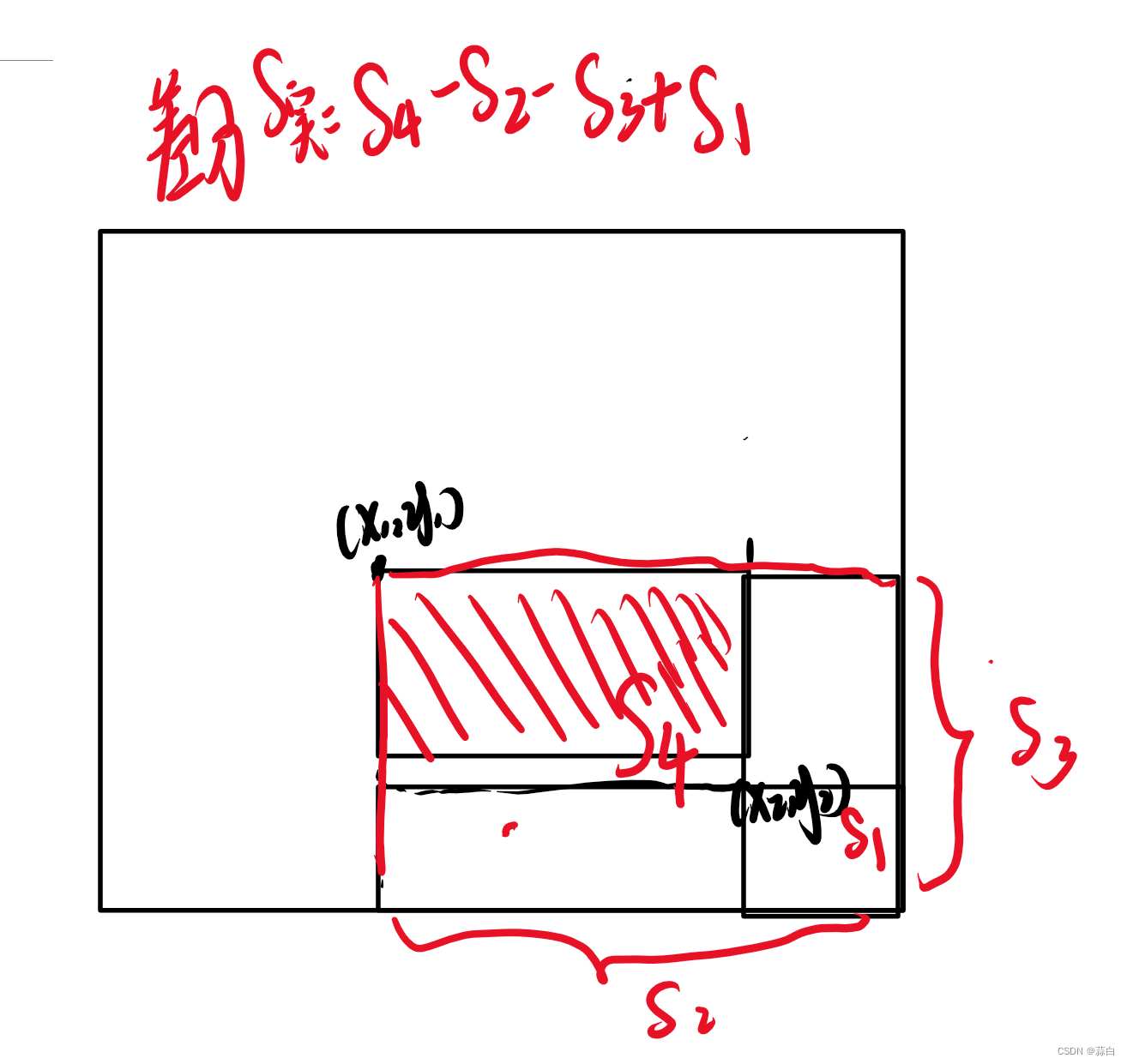
为啥差分是从后面开始进行面积加减呢？
想想我们之前提到的

但是我们现在有了差分数组，我们就不用对 a [N ]做直接修改了，我们从它的差分数组入手，对 b[left] 进行修改，那么 a[ i ] ,a [ i+1 ] ,a [ i+2 ], a [ i+3] …就会发生改变，但是我们不能让改变一直延续下去，所以要在 b [ right ]处进行修改 【及时进行相反的操作,这样就实现了范围修改

差分会对后面的前缀和数组造成影响，对前面的不会影响，一维的数组适用，二维的数组同样适用

题目描述

输入一个 n 行 m 列的整数矩阵，再输入 q
个操作，每个操作包含五个整数 x1,y1,x2,y2,c，其中 (x1,y1)
和 (x2,y2) 表示一个子矩阵的左上角坐标和右下角坐标。

每个操作都要将选中的子矩阵中的每个元素的值加上 c

请你将进行完所有操作后的矩阵输出。

输入格式
第一行包含整数 n,m,q接下来 n 行，每行包含 m
个整数，表示整数矩阵。

接下来 q 行，每行包含 5 个整数 x1,y1,x2,y2,c，表示一个操作。

输出格式
共 n 行，每行 m 个整数，表示所有操作进行完毕后的最终矩阵。

数据范围
1≤n,m≤1000
1≤q≤100000
1≤x1≤x2≤n
1≤y1≤y2≤m
−1000≤c≤1000
−1000≤矩阵内元素的值≤1000
输入样例：
3 4 3
1 2 2 1
3 2 2 1
1 1 1 1
1 1 2 2 1
1 3 2 3 2
3 1 3 4 1
输出样例：
2 3 4 1
4 3 4 1
2 2 2 2
直接上代码

代码

#include<iostream>
using namespace std;
const int N =1e3 +7;
int a[N][N],b[N][N];
int n,m,q;
//这里是对 b 数组进行操作，相当于在(x1,y1)->(x2,y2)范围内加上c
void add(int x1,int y1,int x2,int y2,int c){
    b[x2+1][y2+1]+=c;
    b[x1][y1]+=c;
    b[x2+1][y1]-=c;
    b[x1][y2+1]-=c;
    //这里的操作可以参考之前关于差分的描述 
}
int main(){
    cin>>n>>m>>q;
    for(int i=1;i<=n;i++){
        for(int j=1;j<=m;j++){
            cin>>a[i][j];
            add(i,j,i,j,a[i][j]);
            //通过这个操作只会对 b[i][j]
            //那个点产生影响
        }
    }
    
    while(q--){
        int x1,y1,x2,y2,c;
        cin>>x1>>y1>>x2>>y2>>c;
        add(x1,y1,x2,y2,c);
        
    }
    for(int i=1;i<=n;i++){
        for(int j=1;j<=m;j++){
            b[i][j]+=b[i-1][j]+b[i][j-1]-b[i-1][j-1];
            //这个是前缀和矩阵的计算公式，建议和之前的一维数组类比一下
            cout<<b[i][j]<<' ';
        }
        puts("");
    }
    return 0;
}