前言

本文总结了力扣141.环形链表|以及142.环形链表||这两道有关环形链表的求解方案，去求证链表是否带环已经如何找出入环口的结点。
有关环形链表，在BAT等大厂面试中均有出现，一般是属于中等难度的题，需掌握

环形链表| && 环形链表||

一、题目描述
二、思路分析与罗列
三、证明：
- 1、【为何快指针每次走两步，慢指针走一步一定能相遇？】
- 2、【快指针一次走3步，走4步，...n步行吗？】
四、进阶:如何求出环的入口结点
- 头结点到入口结点的距离剖析求证
五、疑难解惑：为什么快指针会在慢指针进入环内的第一圈就相遇？
- 原理图
六、整体代码展示
- 1、环形链表|
- 2、环形链表||
七、总结与提炼

一、题目描述

原题传送门

给你一个链表的头节点 head ，判断链表中是否有环。

如果链表中有某个节点，可以通过连续跟踪 next 指针再次到达，则链表中存在环。为了表示给定链表中的环，评测系统内部使用整数 pos 来表示链表尾连接到链表中的位置（索引从 0 开始）。注意：pos 不作为参数进行传递。仅仅是为了标识链表的实际情况。

如果链表中存在环，则返回 true 。否则，返回 false 。

示例 1：
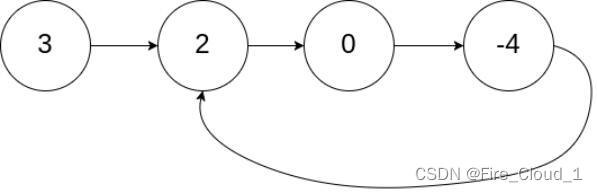
在这里插入图片描述

输入：head = [3,2,0,-4], pos = 1
输出：true
解释：链表中有一个环，其尾部连接到第二个节点。

示例 2：

在这里插入图片描述

输入：head = [1,2], pos = 0
输出：true
解释：链表中有一个环，其尾部连接到第一个节点。

示例 3：
在这里插入图片描述

输入：head = [1], pos = -1
输出：false
解释：链表中没有环。

提示：

链表中节点的数目范围是 [0, 104]
-105 <= Node.val <= 105
pos 为 -1 或者链表中的一个有效索引。

二、思路分析与罗列

好，看完了题目描述，接下去我们来分析一下如何去求解这道题目

首先对于此题，首先你要考虑的一点是怎么去判断一个链表是否有环?
在一开始看题目的时候你可能想了很多的办法，但是当写代码的时候，发现又不对。有点同学就和我说：这不是很简单，搞一个指针，做一个遍历，若是若是这个指针又回到原来的交点，那不就是带环吗
那我只能说，这个同学没有读清楚题目，题目并没有告诉你这个环的入口在哪里，你怎么去判断这个遍历的指针走了一圈呢？所以这都是无稽之谈，我们应该通过画图来进行分析

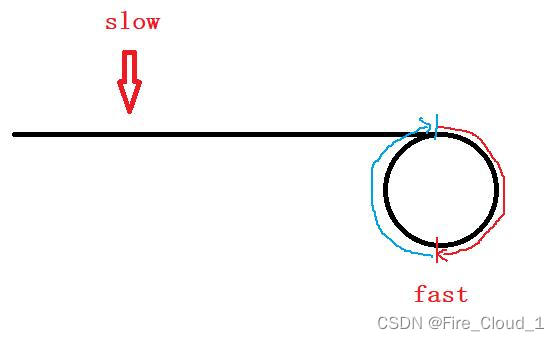
从上述图中可以看到，我使用来一个叫做快慢指针，这其实是解决环形链表这种问题的最好手段，具体的思路就是让快慢指针同时遍历这个链表，快指针走两步，慢指针走一步，然后在不断遍历的过程中，若是两个指针重合了，说明链表带环，具体的证明我放在后面讲解
我们先来看一下快慢指针是如何遍历的

【牢记规则：快指针走两步，慢指针走一步】

好，通过上面的算法图示，相信你已经明白了快慢指针最后究竟是如何相遇的，这个光凭空想还真的不好想出来，但是我们画个图来分析一下，就非常地明确了。我们在下一模块来写写代码

class Solution {
public:
    bool hasCycle(ListNode *head) {
        ListNode* fast, *slow;
        fast = slow = head;

        while(fast && fast->next)       //判断奇数和偶数个结点的情况
        {
            slow = slow->next;
            fast = fast->next->next;

            if(fast == slow)
                return true;
        }
        return false;
    }
};

可以看出，代码并不复杂，就是通过一个循环去让这两个快慢指针去遍历这个链表，若是它们相遇，则【return true】，若是循环遍历结束还是没有遇见，则说明链表不带环

三、证明：

1、【为何快指针每次走两步，慢指针走一步一定能相遇？】

相信在看完我上面的一些简略分析后有些小伙伴一定会疑惑为什么快指针每次走两步，慢指针每次走一步一定能相遇
首先我在这里做一个假设，就是当快指针已经入环，而慢指针刚好入环时，他们之间的距离相差N

然后此时缩小快慢指针的宏观移动距离，然后观察两个指针的移动的是否会改变他们之间的距离
首先记录下它们的第一次移动①

然后是第二次移动，继续计算它们之间的距离

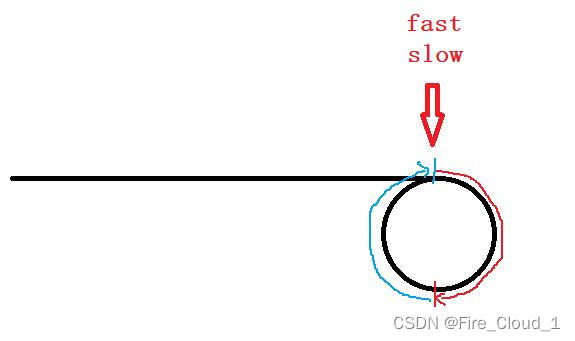
于是我们可以得出来下面这个结论，快指针【fast】和慢指针【slow】在不断前进的过程中它们之间的距离是会不断缩短的，当它们之间的距离 = 0时，其实也就意味着它们相交了
其实快指针就是一个不断在追逐慢指针的一个过程

所以就可以证明这个结论——》【快指针每次走两步，慢指针走一步一定能相遇】

2、【快指针一次走3步，走4步，…n步行吗？】

接下去我们再来证明一个问题，刚才快指针一次是走两步，一定能追上，那现在当这个快指针一次走3步、走4步能不能追得上呢？我们一起来分析一下
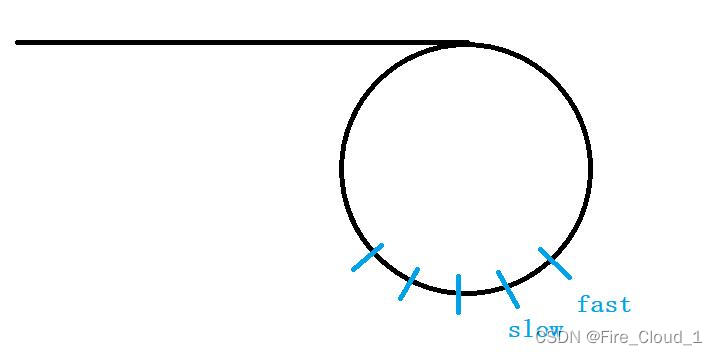
情况有很多，我这里就拿【fast】走3步，【slow】走1步来进行一个证明

那根据我们上一个问题的证明，这依旧设【fast】在环中当【slow】刚进环时两者之间的距离为N，然后就可以得到两者在追击时它们之间的距离每次会缩短2，然后就可以去计算它们可不可能相遇
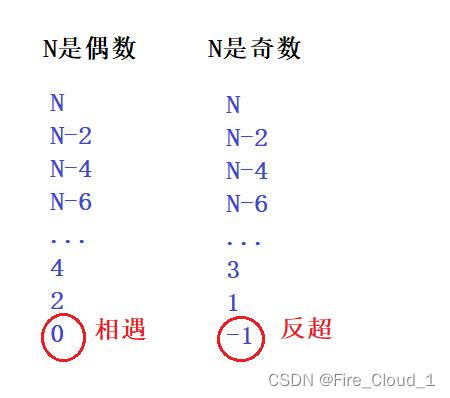
因为它们之间的距离每次缩短的长度是一致的，所以就需要看这个N的大小，也就是在环中【fast】和【slow】之间的距离，若是N为偶数，那最后它们之间的距离一定会减少到0，也就意味着相遇；若是N为奇数，那最后它们之间的距离一定会减少到-1，这就意味着【fast】追是追上【slow】，但是呢却刚好错过了，到达了它的前一位

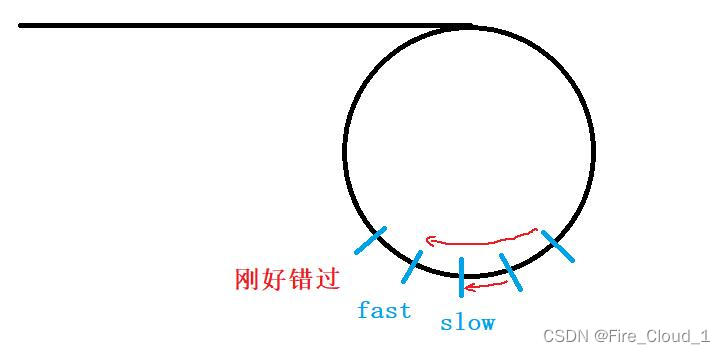
我们来做一个模拟，此时当【fast】和【slow】快相遇时，它们继续行走

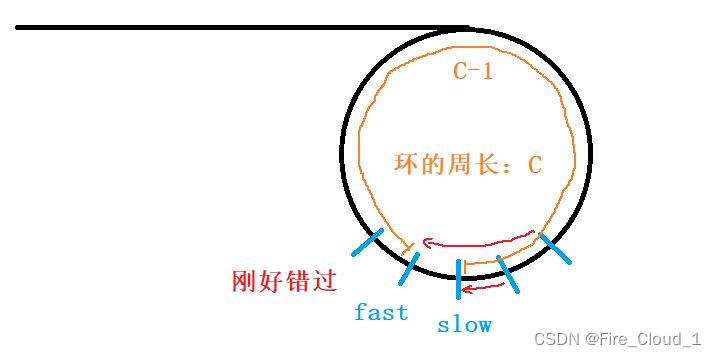
OK，可以看到，它们确实是错过了，那此时它们之间距离是多少呢?设整个环的周长为C。此时它们之间的距离就变成了【C-1】
此时就需要在【C-1】的基础上再去考虑它们会不会相遇，那其实也是一样的道理，当【C-1】为偶数时，它们会相遇，当【C-1】为奇数时，它们之间的距离依旧会变回【C-1】，此时真的就变成一个环了，两个指针在里面绕来绕去就是不会相交，【fast】永远都追不上【slow】

那这个问题的其他示例其实也是一样，比如说快指针每次走5步、走6步，慢指针走个2步、3步，其实都是一个道理，只不过要进行一个取余运算，最后的结果还是一样，只要他们之间的距离为奇数，那么就永远追不上

【最后我们可以得出结论：当两个指针的相对速度为1时，一定能相遇；当两个指针的相对速度> 1时，则需要视两个指针之间的距离而定】

四、进阶:如何求出环的入口结点

此进阶为是环形链表|的后一道题👉142.环形链表||，可先看看原题

头结点到入口结点的距离剖析求证

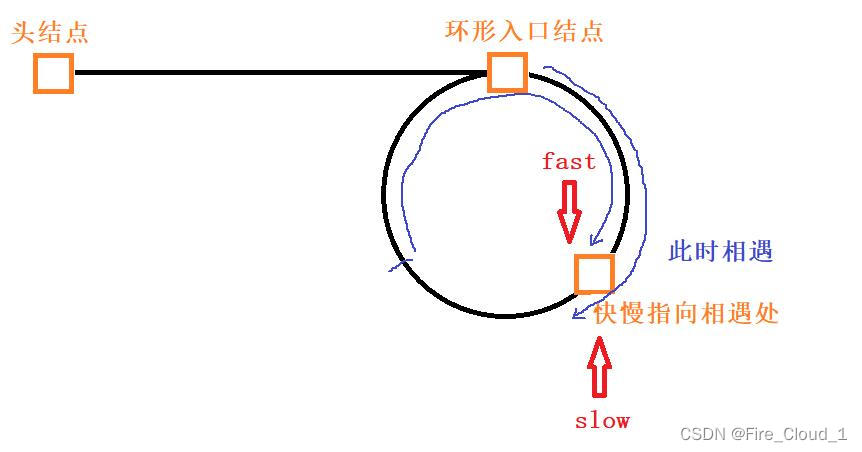
好，看完了如何去证明一些环内快慢指针相遇的问题，接下去我们继续深入，从我画的图里可看到，从链表的头结点过来有一个环，而且我标出了一个结点叫做【环的入口结点】，也就是那位同学说的从这个结点开始遍历去判断这个链表是否有环
那我们该如何去求解这个环呢？这需要一个数学分析和推理验算的思维，听我给你讲一讲:📖
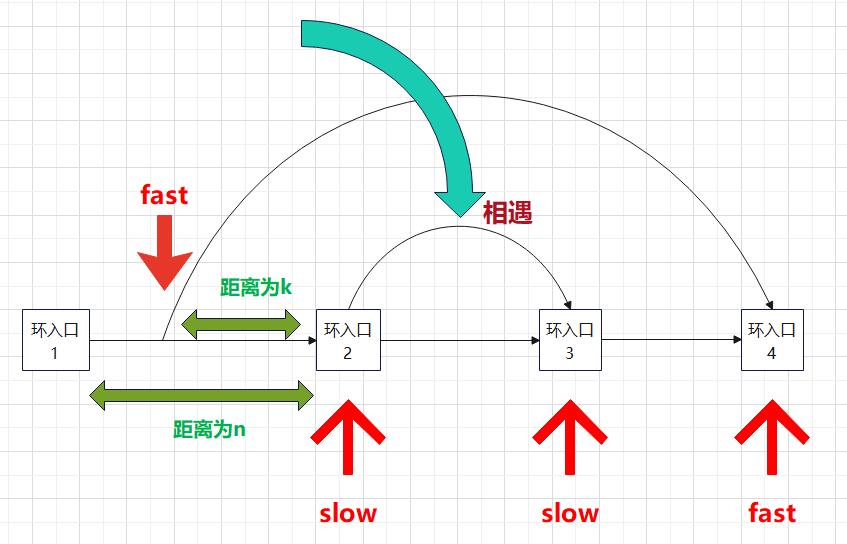
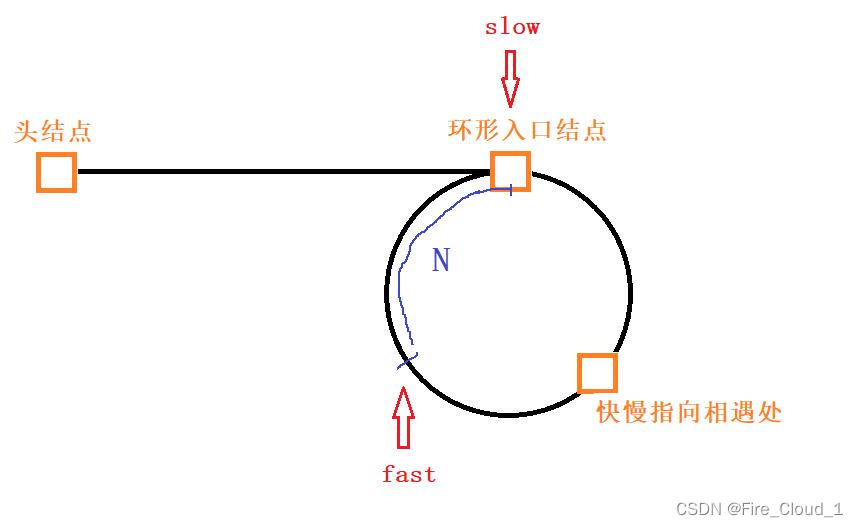
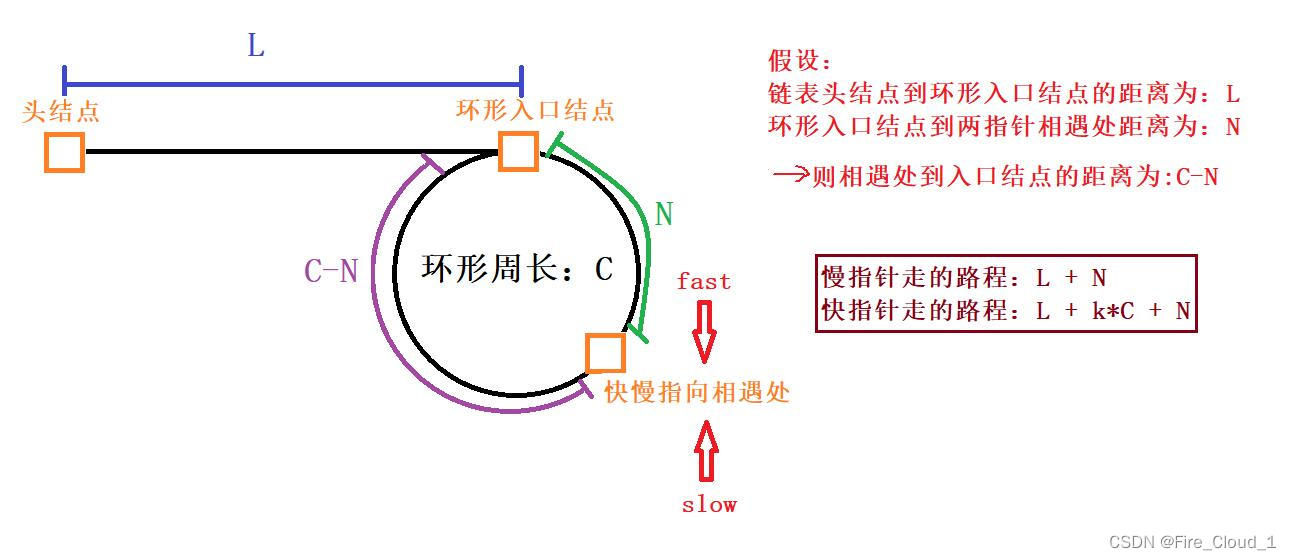
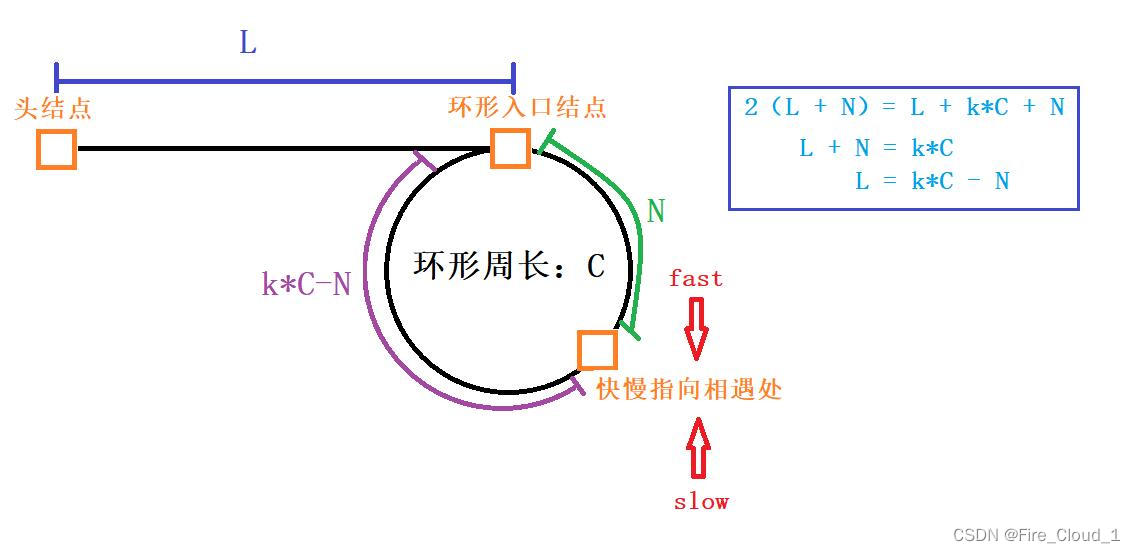
首先我们做一个假设，从链表头结点开始到环形入口结点的距离为L，从入口结点到快慢指针相遇的距离为N，则从相遇处再到入口结点的距离就为C-N
此时我们需要根据这些长度变量去写出慢指针和快指针到相遇为止走过的距离

慢指针走过的路程根据我们上面的推论很好计算，就是【L + N】，而对于快指针来说，很多同学就会有所异或了，因为它是在追慢指针的一个过程，但是不知道它在经过了多少距离，于是有的同学就直接认为快指针走过的距离为【L + C + N】，也就是快指针在环中刚好走了一圈碰到慢指针，然后根据快慢指针的两倍关系，就得出L = C - N，其实这还是有所考虑不周，可能是我画的这个环误导他了，下面我在换一个环来看看

可以看到，这环很小，我们设快指针走一步为半个环

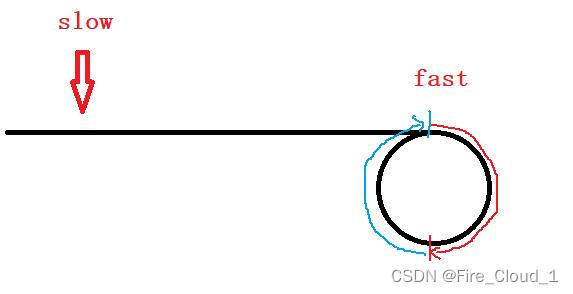
可以看到此时快指针已经走了一圈，要开始走第二圈

然后经过一段时间后，他们终究会相遇，但此时快指针【fast】已经在环里走了好几圈了，因此这就是我们要考虑到的情况，当这个环很大的时候，可能环很大的时候，【fast】走上个一圈就可以遇到【slow】，但是当这个环很小的时候，【fast】就需要等待【slow】，于是它会在这个小环里一直走一直走，直到他们在环的入口点相遇为止
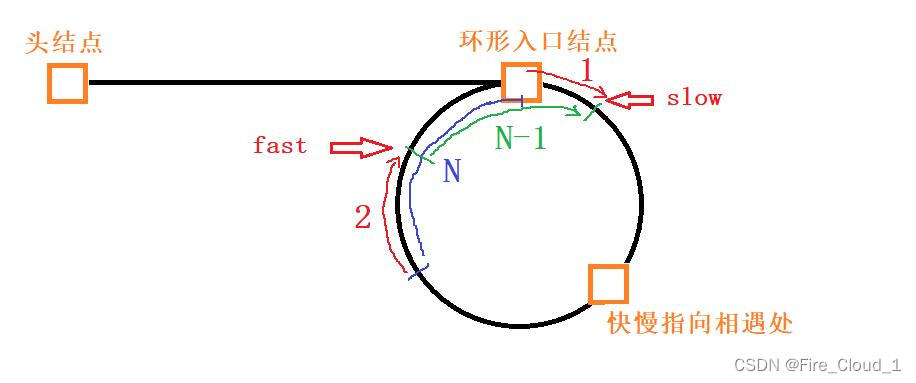
然后我们就可以精确地分析出快指针所走的路程，即为【L + k*C + N】，k是快指针走了几圈，C是周长。于是我们就可以根据快慢指针的两倍关系得出从头结点到环形入口结点的距离L

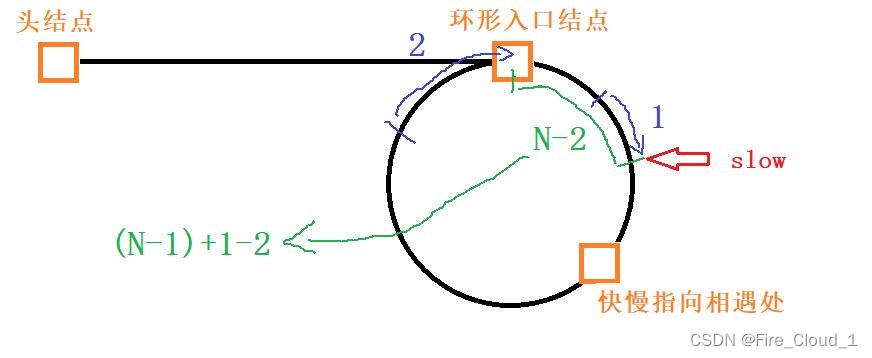
那其实这个快指针不是走了k圈，而是走了【k - 1】圈，因此我们可以将k用【k - 1】带入可得L = (k - 1)*C - N，为了和原本的等式相同，于是加上C，变为【L = (k - 1)*C + (C - N)】
此时我们就可以拿这个式子去分析了，当【k = 1】时，也就是快指针走了一圈时，L就等于【C - N】，那也就是我们一开始算的从快慢指针相遇处到环形入口结点之间的距离，当【k > 1】时，就需要另加考虑，让快指针先走上k圈，然后再用环的周长 - N，此时才是L的长度

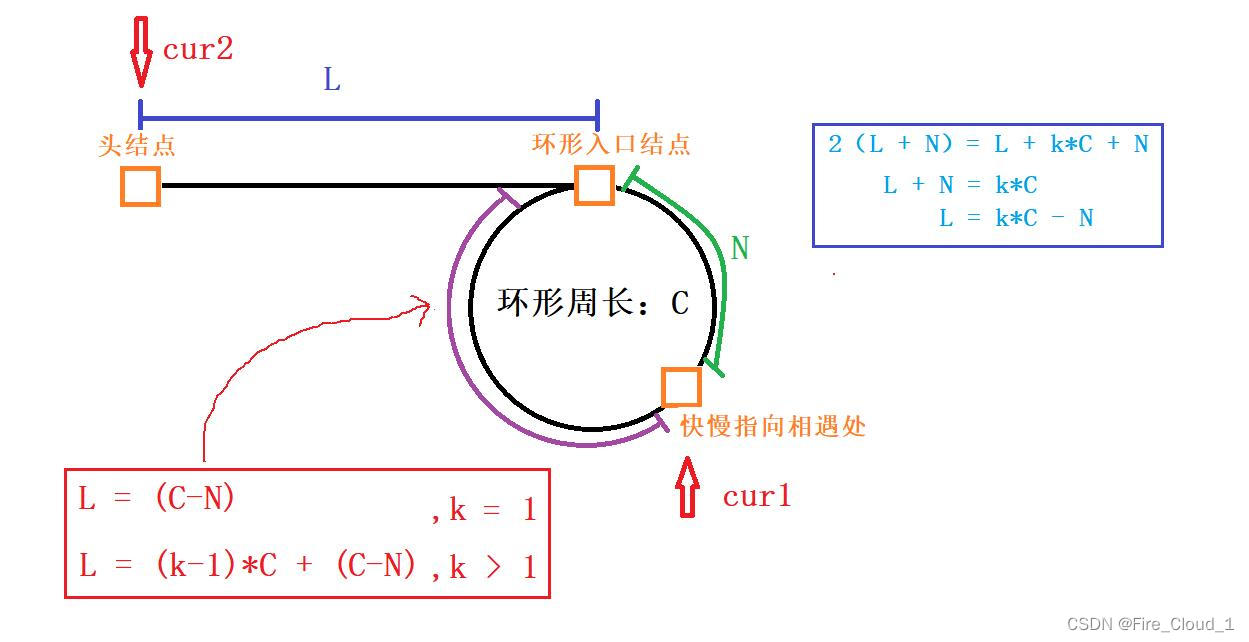
那这个时候有同学问了，求出这段L的长度有什么用呢？对于，有什么用。其实我就是在证明在快慢指针已经相遇后要如何行走才可以到达这个环的入口现在我们得出一个表达式为【L = (k - 1)*C + (C - N)】

那我们可以在快慢指针的相遇处定义一个指针【cur1】，在结点处再定义一个指针【cur2】，然后让他们一直走一直走，通过这个环的大小来看出【cur1】会在这个环里转多少圈。我们来看一下代码

ListNode *detectCycle(ListNode *head) {
    ListNode* slow, *fast;
    fast = slow = head;
    while(fast && fast->next)
    {
        slow = slow->next;
        fast = fast->next->next;
        if(slow == fast)
        {
            ListNode* cur1 = fast;
            ListNode* cur2 = head;
            while(cur1 != cur2)
            {
                cur1 = cur1->next;
                cur2 = cur2->next;
            }
            return cur1;
        }
    }
    return NULL;
}

可以看出，代码并不难写，只是我们在分析证明的时候花了很大的心思

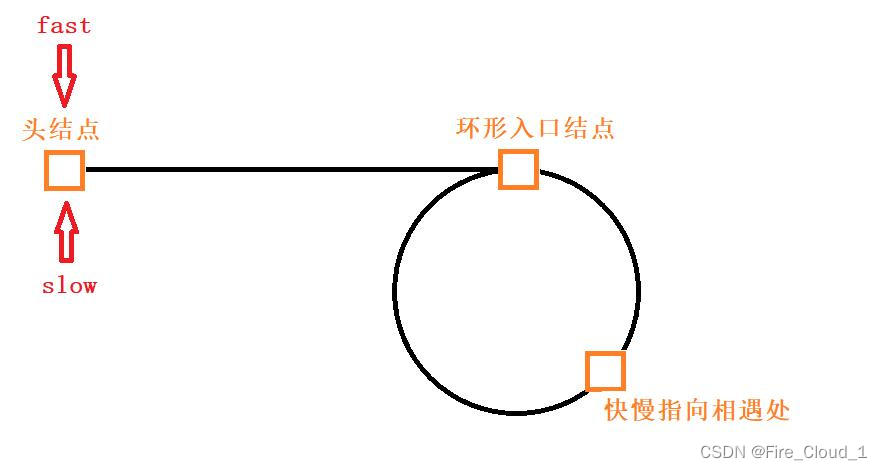
五、疑难解惑：为什么快指针会在慢指针进入环内的第一圈就相遇？

有些小伙伴可能还是对快指针为何会在慢指针进到环里但是还没有碰到环的出口时就会相遇，我们来继续探究一下🔍

因为快指针一定是先进入环内的，然后慢指针才进到环内，然后当慢指针进入下一个入口时，快指针走的一定是慢指针的两倍，所以慢指针在没有进入到下一个入口处时，快指针在中间的某个位置一定和其相遇了

证明如下：

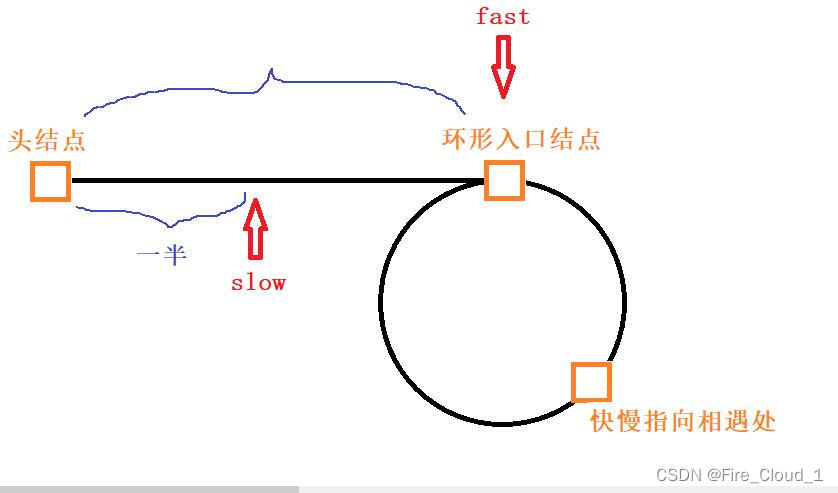
在快指针fast进入环口3时，它已经走了k + n个结点，从图中可以清晰地看出，k为快指针和慢指针之间的距离，n为一个环的距离，而慢指针在进入环内相应地走了(k + n)/2个结点，从图中可以看出k是小于n的，所以(k + n)/2也一样是小于n的，即慢指针在进入环内一圈不到的距离就会和快指针相遇

所以慢指针走动的距离为L + N就够了，其不会再走第二圈

原理图

请添加图片描述

六、整体代码展示

1、环形链表|

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode(int x) : val(x), next(NULL) {}
 * };
 */
class Solution {
public:
    bool hasCycle(ListNode *head) {
        ListNode* fast, *slow;
        fast = slow = head;

        while(fast && fast->next)       //判断奇数和偶数个结点的情况
        {
            slow = slow->next;
            fast = fast->next->next;

            if(fast == slow)
                return true;
        }
        return false;
    }
};

2、环形链表||

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode(int x) : val(x), next(NULL) {}
 * };
 */
class Solution {
public:
    ListNode *detectCycle(ListNode *head) {
        ListNode* slow, *fast;
        fast = slow = head;
        while(fast && fast->next)
        {
            slow = slow->next;
            fast = fast->next->next;
            if(slow == fast)
            {
                ListNode* cur1 = fast;
                ListNode* cur2 = head;
                while(cur1 != cur2)
                {
                    cur1 = cur1->next;
                    cur2 = cur2->next;
                }
                return cur1;
            }
        }
        return NULL;
    }
};

七、总结与提炼

最后我们来总结一下本文所介绍的内容，本文我们探究了链表章节比较复杂的一种题型——环形链表，这也是BAT等大厂在面试时很喜欢出的算法题，不仅仅是会让你手写代码，而且还会让你现场做个证明，因此对于上述的一些证明，希望大家也可以搞懂
我们知道，编程的核心是算法，算法的本质是数学，你数学好了，逻辑思维就能强，面对一些棘手的推理算法题时才能游刃有余