需要源码请点赞关注收藏后评论区留言私信~~~

欠拟合、过拟合与泛化能力

欠拟合

最简单的线性模型，它是用一条直线来逼近各个样本点，显然力不从心，这种现象称为欠拟合。欠拟合模型是由于模型复杂度不够，训练样本集容量不够，特征数量不够，抽样分布不均衡等原因引起的不能学习出样本集中蕴含只是的模型，欠拟合问题比较容易处理，如增加模型复杂度，增加训练样本，提取更多特征等等

过拟合

 

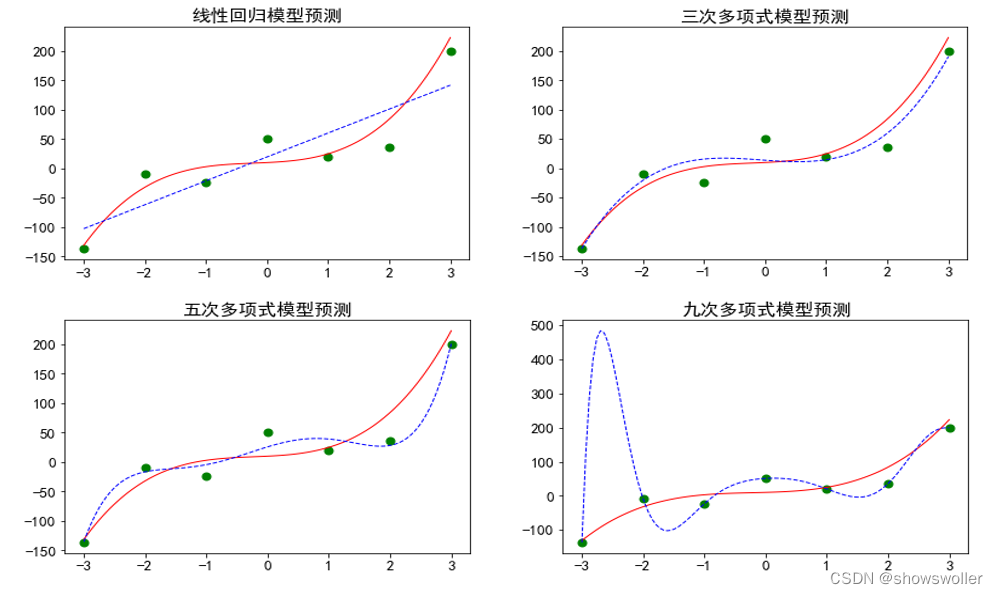
某些情况下，越复杂的模型越能逼近样本点，但也越背离作为目标的三次多项式函数，这样的模型在 训练集上表现很好，而在测试集上表现很差，这种现象称为过拟合，产生过拟合的原因是模型过于复杂，以至于学习过多了，把噪声的特征也学习进去了

在示例中，采用均方误差作为损失函数，因此，训练误差就是所有训练样本的误差平方的均值。同样，测试误差是所有测试样本的误差平方的均值。

 

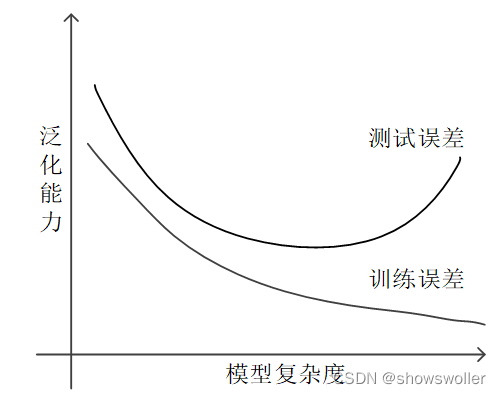
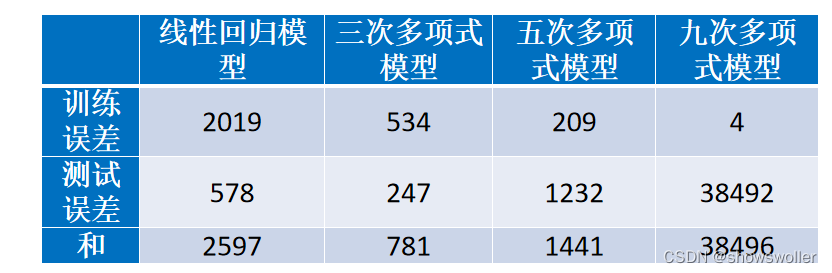
 过拟合抑制

在算法研究中，解决过拟合问题时，常提到一个所谓的“奥卡姆剃刀（Occam's Razor）定律”，它是由14世纪逻辑学家奥卡姆提出的。这个定律称为“如无必要，勿增实体”，即“简单有效原理”。在模型选择中，就是在所有可以选择的模型中，能够很好地解释已知数据并且简单的模型才是最好的模型。基于这个思路，在算法研究中，人们常采用正则化（regularization）、早停（early stopping）、随机失活（dropout）等方法来抑制过拟合。

1：正则化方法

正则化方法是在样本集的损失函数中增加一个正则化项（regularizer），或者称罚项（penalty term），来对冲模型的复杂度。正则化项一般是模型复杂度的单调递增函数，模型越复杂，正则化值就越大。

正则化方法的优化目标为：

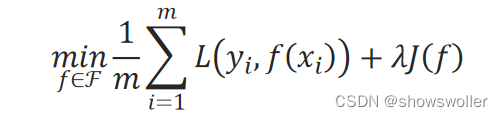
其中，f代表某一模型，ℱ是可选模型的集合，L是损失函数。第一项1/m∑_i=1^m▒L(y_i,f(x_i))是训练集上的平均损失，即训练误差，第二项J(f)是正则化项，λ≥0为正则化项的权重系数。

常用的正则化方法有L1范数、L2范数正则化方法。向量的范数一般用来衡量向量的大小，对于n维向量x={x^(1),x^(2),…,x^(n)}，其L_p范数定义为：

 

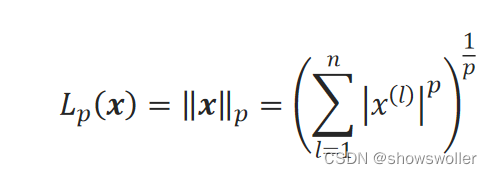
 直观来看，向量的L2范数就是它在欧氏空间中的点到原点的距离。

L2范数正则化方法

设原始损失函数是L_0，给它加一个正则化项，该正则化项是模型所有参数组成的向量W=(w^(0) w^(1) … w^(k))的L2范数的函数。新的损失函数为：

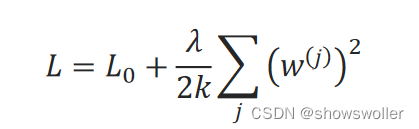
λ是正则化项的权重系数。k是所有参数的数量，它在一个模型中是一个常量，也可以不除，乘以1∕2是为了求导后消除常数2。

 

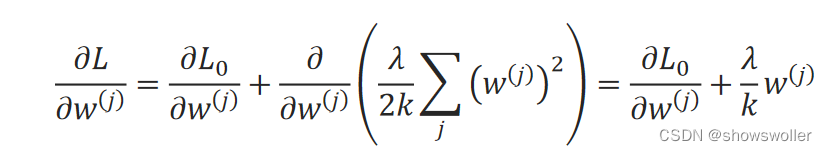
梯度下降法的迭代关系式：

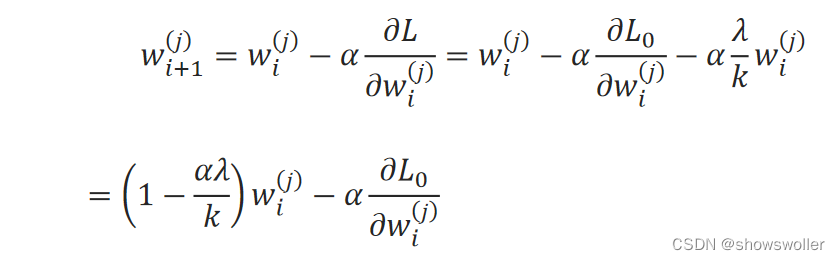
 可见，使用该正则项后，w_i^(j)的系数小于1了，因此，将使得w_i+1^(j)较原来的变化要小一些，这个方法也叫权重衰减（weight decay）。 采用L2范数正则项的线性回归，称为岭回归。

L1范数正则化方法

L1范数正则化方法是如下形式：

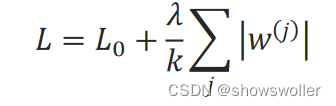
对w^(j)求导：

 

sgn是符号函数：

 

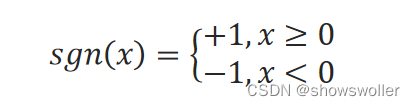
梯度下降法的迭代式为：

 

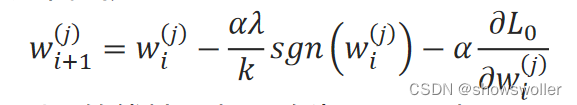
2：早停法 

早停法是在模型迭代训练中，在模型对训练样本集收敛之前就停止迭代以防止过拟合的方法。

模型泛化能力评估的思路是将样本集划分为训练集和验证集，用训练集来训练模型，训练完成后，用验证集来验证模型的泛化能力。而早停法提前引入验证集来验证模型的泛化能力，即在每一轮训练（一轮是指遍历所有训练样本一次）完后，就用验证集来验证泛化能力，如果n轮训练都没有使泛化能力得到提高，就停止训练。n是根据经验提前设定的参数，常取10、20、30等值。这种策略称为“No-improvement-in-n”。

3：随机失活法

随机失活只应用于人工神经网络的过拟合抑制，它通过随机使一部分神经元临时失效来达到目的。

4：工程方法

在工程方面，可以从样本集数据方面采取措施来防止过拟合，包括数据清洗（data cleaning）和数据扩增（data augmentation）等。数据清洗是指尽量清除掉噪声，以减少对模型的影响。数据扩增是指增加训练样本来抵消噪声的影响，从而抑制过拟合。增加训练样本包括从数据源采集更多的样本和人工制造训练样本两种方法。在人工制造训练样本时，要注意制造的样本要和已有样本是近似独立同分布的。

部分代码如下

from sklearn.preprocessing import PolynomialFeatures
featurizer_5 = PolynomialFeatures(degree=5)
x_5 = featurizer_5.fit_transform(x)
x_p_5 = featurizer_5.transform(x_p)
model_5 = LinearRegression()
model_5.fit(x_5, y)
print('--五次多项式模型--')
print('训练集预测值与样本的残差均方值：' + str(np.mean((model_5.predict(x_5)-y)**2)))
print('测试集预测值与目标函数值的残差均方值：' + str(np.mean((model_5.predict(x_p_5)-myfun(x_p))**2)))
print('系数：' + str(model_5.coef_))
print('截距：' + str(model_5.intercept_))

plt.title(u'五次多项式模型预测')
plt.scatter(x, y, color="green", linewidth=2)
plt.plot(x1, y0, color="red", linewidth=1)
#y1 = model.predict(x1)
#plt.plot(x1, y1, color="black", linewidth=1)
#y3 = model_3.predict(featurizer_3.fit_transform(x1))
#plt.plot(x1, y3, "b--", linewidth=1)
y5 = model_5.predict(featurizer_5.fit_transform(x1))
plt.plot(x1, y5, "b--", linewidth=1)
plt.show()
fro_9 = PolynomialFeatures(degree=9)
x_9 = featurizer_9.fit_transform(x)
x_p_9 = featurizer_9.transform(x_p)
model_9 = LinearRegression()
model_9.fit(x_9, y)
print('--九次多项式模型--')
print('训练集预测值与样本的残差均方值：' + str(np.mean((model_9.predict(x_9)-y)**2)))
print('测试集预测值与目标函数值的残差均方值：' + str(np.mean((model_9.predict(x_p_9)-myfun(x_p))**2)))
print('系数：' + str(model_9.coef_))
print('截距：' + str(model_9.intercept_))

plt.title(u'九次多项式模型预测')
plt.scatter(x, y, color="green", linewidth=2)
plt.plot(x1, y0, color="red", linewidth=1)
#y1 = model.predict(x1)
#plt.plot(, "b--", linewidth=1)
y9 = model_9.predict(featurizer_9.fit_transform(x1))
plt.plot(x1, y9, "b--", linewidth=1)
plt.show()

创作不易 觉得有帮助请点赞关注收藏~~~