题目

标题和出处

标题：环形链表

出处：141. 环形链表

难度

2 级

题目描述

要求

给你一个链表的头结点 $\text{head}$，判断链表中是否有环。

如果链表中有某个结点，可以通过连续跟踪 $\text{next}$ 指针再次到达，则链表中存在环。评测系统内部使用 $\text{pos}$ 表示链表尾结点的 $\text{next}$ 指针连接到的结点下标（下标从 $\text{0}$ 开始）。如果 $\text{pos}$ 是 $\text{-1}$，则在该链表中没有环。注意 $\text{pos}$ 不作为参数进行传递。

如果链表中存在环，则返回 $\text{true}$。否则，返回 $\text{false}$。

示例

示例 1：

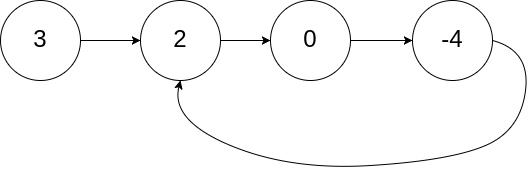
输入：$\text{head = [3,2,0,-4], pos = 1}$
输出：$\text{true}$
解释：链表中有一个环，其尾部连接到第 $\text{1}$ 个结点。

示例 2：

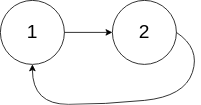
输入：$\text{head = [1,2], pos = 0}$
输出：$\text{true}$
解释：链表中有一个环，其尾部连接到第 $\text{0}$ 个结点。

示例 3：

输入：$\text{head = [1], pos = -1}$
输出：$\text{false}$
解释：链表中没有环。

数据范围

• 链表中结点的数目范围是 ${\text{[0, 10}}^{\text{4}}\text{]}$
• ${\text{-10}}^{\text{5}}\le \text{Node.val}\le {\text{10}}^{\text{5}}$
• $\text{pos}$ 为 $\text{-1}$ 或者链表中的一个有效下标

进阶

你是否可以使用 $\text{O(1)}$ 空间解决此问题？

解法一

思路和算法

如果链表中存在环，则链表的尾结点的 $\text{next}$ 指针指向链表中的一个结点，被指向的结点为链表开始入环的结点。从链表的头结点 $\text{head}$ 开始遍历链表，如果链表存在环，则在访问尾结点之后会重复访问链表开始入环的结点。

如果链表中没有环，则任何结点都不会被重复访问。

因此可以遍历链表，根据是否有结点被重复访问判断链表中是否有环。为了判断是否有结点被重复访问，可以使用哈希集合存储访问过的结点。

在遍历链表的过程中将访问到的每个结点加入哈希集合。如果在遍历过程中遇到一个结点已经在哈希集合中，则链表中存在环，返回 $\text{true}$。如果遍历链表结束到达 $\text{null}$ 时仍没有遇到已经在哈希集合中的结点，则链表中没有环，返回 $\text{false}$。

代码

public class Solution {
    public boolean hasCycle(ListNode head) {
        Set<ListNode> visited = new HashSet<ListNode>();
        ListNode temp = head;
        while (temp != null) {
            if (!visited.add(temp)) {
                return true;
            }
            temp = temp.next;
        }
        return false;
    }
}

复杂度分析

• 时间复杂度：$O(n)$，其中 $n$ 是链表的结点数。链表中的每个结点最多遍历一次。

• 空间复杂度：$O(n)$，其中 $n$ 是链表的结点数。需要使用哈希集合存储链表中的全部结点。

解法二

思路和算法

判断链表中是否有环的另一个常用的方法是快慢指针。

初始时，快指针和慢指针都位于链表的头结点。每次将快指针移动两步，慢指针移动一步，在至少移动一次的情况下，如果快慢指针相遇则链表中存在环。

如果链表中存在环，则两个指针在移动过程中都会进入环，然后在环内移动。当两个指针都在环内移动时，一定存在一次移动，使得快指针和慢指针相遇。

如果链表中不存在环，则在至少移动一次的情况下，快指针总是在慢指针的前面，快指针将会先到达链表末尾。

由此可以使用快慢指针判断链表中是否有环。将快慢指针同时从链表的头结点开始移动，每次将快指针移动两步，慢指针移动一步，直到遇到终止条件：

1. 在至少移动一次的情况下，如果快慢指针相遇，则链表中存在环，返回 $\text{true}$；

2. 如果快指针到达链表末尾，则链表中没有环，返回 $\text{false}$。

代码

public class Solution {
    public boolean hasCycle(ListNode head) {
        ListNode fast = head, slow = head;
        while (fast != null && fast.next != null) {
            fast = fast.next.next;
            slow = slow.next;
            if (fast == slow) {
                return true;
            }
        }
        return false;
    }
}

复杂度分析

• 时间复杂度：$O(n)$，其中 $n$ 是链表的结点数。
  如果链表中存在环，则从快慢指针都进入环到相遇的移动次数不超过环内的结点数，因此总移动次数不超过链表的结点数。
  如果链表中没有环，则快指针将到达链表末尾，移动次数不超过链表结点数的一半。

• 空间复杂度：$O(1)$。