文章目录
- 一、提出任务 - 最小覆盖圆
-
- 二、完成任务
- (一)编程思路
- (二)编写代码,实现功能
- (三)运行程序,查看结果
一、提出任务 - 最小覆盖圆
(一)描述
- 给出平面上
N
(
N
≤
1
0
2
)
N(N\le10^2)
N(N≤102)个点。请求出一个半径最小的圆覆盖住所有的点。
(二)输入
- 第一行给出数字
N
N
N,接下来
N
N
N行,每行两个实数
x
,
y
x,y
x,y表示其坐标。其中,
−
1
0
5
≤
x
,
y
≤
1
0
5
-10^5\le x,y \le 10^5
−105≤x,y≤105
(三)输出
- 第一行输出最小覆盖医的圆心
- 第二行输出半径
- 输出保留三位小数
(四)样例
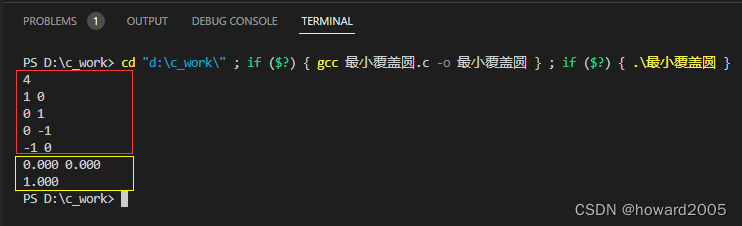
输入
4
1 0
0 1
0 -1
-1 0
输出
0.000 0.000
1.000
二、完成任务
(一)编程思路
- 任意两点间距离的最大值就是最小覆盖圆的直径
- 距离最大值的两个点的中心就是最小覆盖圆的圆心
(二)编写代码,实现功能
- 在
C_WORK目录里创建C程序 - 最小覆盖圆.c
#include "stdio.h"
#include "math.h"
int main()
{
int n;
double distance, maxDistance = 0;
double cx = 0, cy = 0, r;
scanf("%d", &n);
double x[n], y[n];
for (int i = 0; i < n; i++)
{
scanf("%lf %lf", &x[i], &y[i]);
}
for (int i = 0; i < n; i++)
{
for (int j = 0; j < n; j++)
{
distance = sqrt(pow(x[i] - x[j], 2) + pow(y[i] - y[j], 2));
if (maxDistance < distance)
{
maxDistance = distance;
}
}
}
for (int i = 0; i < n; i++)
{
for (int j = 0; j < n; j++)
{
distance = sqrt(pow(x[i] - x[j], 2) + pow(y[i] - y[j], 2));
if (maxDistance == distance)
{
cx = (x[i] + x[j]) / 2;
cy = (y[i] + y[j]) / 2;
break;
}
}
}
r = maxDistance / 2;
4
printf("%.3f %.3f\n", cx, cy);
printf("%.3f\n", r);
return 0;
}
(三)运行程序,查看结果
- 输入4,与四个点坐标


![[附源码]计算机毕业设计Node.js吃天下美食网站(程序+LW)](https://img-blog.csdnimg.cn/1b5ba562ad694088b89cb1d4913417d8.png)