医院设置

题目描述

设有一棵二叉树，如图：

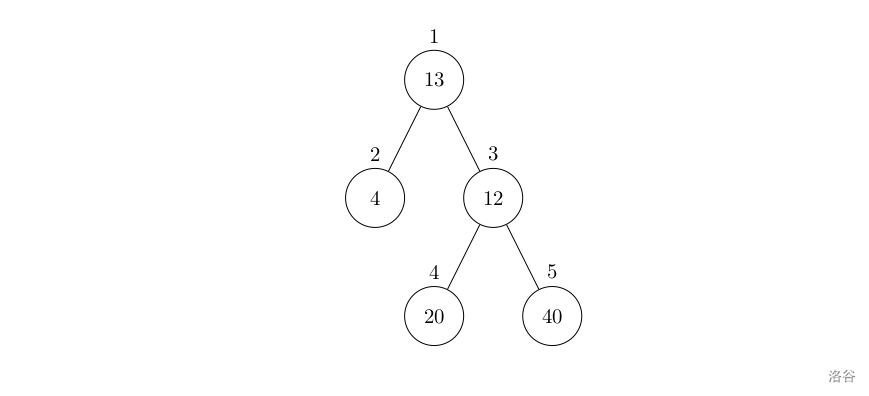
其中，圈中的数字表示结点中居民的人口。圈边上数字表示结点编号，现在要求在某个结点上建立一个医院，使所有居民所走的路程之和为最小，同时约定，相邻接点之间的距离为 $1$。如上图中，若医院建在 $1$ 处，则距离和 $=4+12+2\times 20+2\times 40=136$；若医院建在 $3$ 处，则距离和 $=4\times 2+13+20+40=81$。

输入格式

第一行一个整数 $n$，表示树的结点数。

接下来的 $n$ 行每行描述了一个结点的状况，包含三个整数 $w,u,v$，其中 $w$ 为居民人口数，$u$ 为左链接（为 $0$ 表示无链接），$v$ 为右链接（为 $0$ 表示无链接）。

输出格式

一个整数，表示最小距离和。

样例 #1

样例输入 #1

5						
13 2 3
4 0 0
12 4 5
20 0 0
40 0 0

样例输出 #1

81

提示

数据规模与约定

对于 $100\%$ 的数据，保证 $1\le n\le 100$，$0\le u,v\le n$，$1\le w\le 10^5$。

---

思路

将二叉树储存为一张图，存图时要存双向边。

暴力枚举每个节点作为医院，然后分别计算所有节点到这个医院的距离的加权和。

使用 DFS 遍历整张图，对于当前遍历的节点 $x$，用一个变量 $sum$ 记录所有已经遍历的节点到当前节点 $x$ 的距离的加权和，用一个 bitset 变量 $vis$ 记录所有已经遍历过的节点，然后递归地遍历 $x$ 的所有邻接节点，计算它们到 $x$ 的距离的加权和，并将其加到 $sum$ 上。

为了避免重复遍历已经遍历过的节点，并方便计算节点到达医院的距离，需要在遍历之前将 $vis[x]$ 设为 $1$，在遍历之后再将其设为 $0$。

遍历完所有的节点后，用一个变量 $ans$ 记录所有节点作为医院时的最小距离和，然后每次更新 $ans=\min (ans,sum)$。最后输出 $ans$ 即可。

---

AC代码

#include <iostream>
#include <bitset>
#include <algorithm>
#include <cstring>
#define AUTHOR "HEX9CF"
using namespace std;

const int N = 1005;

// 链式前向星
struct Sedge
{
    int to;
    int next;
} edge[N];
int head[N];
int cnt = 0;
int w[N];

int n;
int tmp;
int sum;
int ans;

bitset<N> vis;

void add(int u, int v)
{
    if (u && v)
    {
        edge[cnt].to = v;
        edge[cnt].next = head[u];
        head[u] = cnt++;
    }
}

void dfs(int x)
{
    if (vis[x])
    {
        return;
    }
    sum += w[x] * vis.count();
    // cout << x << endl;
    vis[x] = 1;
    for (int i = head[x]; ~i; i = edge[i].next)
    {
        dfs(edge[i].to);
    }
    vis[x] = 0;
}

int main()
{
    memset(head, -1, sizeof(head));
    cin >> n;
    for (int i = 1; i <= n; i++)
    {
        int a, b;
        cin >> w[i] >> a >> b;
        add(i, a);
        add(i, b);
        add(a, i);
        add(b, i);
    }
    for (int i = 1; i <= n; i++)
    {
        sum = 0;
        vis.reset();
        dfs(i);
        if (1 == i)
        {
            ans = sum;
        }
        else
        {
            ans = min(ans, sum);
        }
        // cout << sum << endl;
    }
    cout << ans << endl;
    return 0;
}