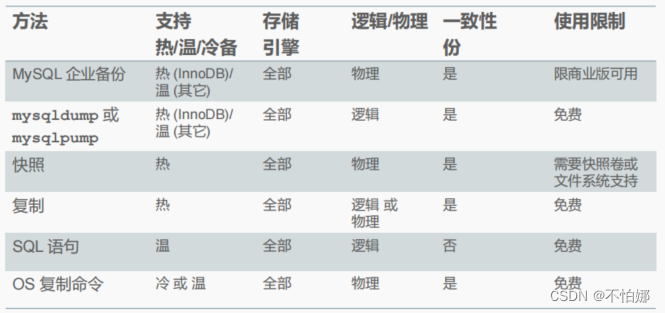
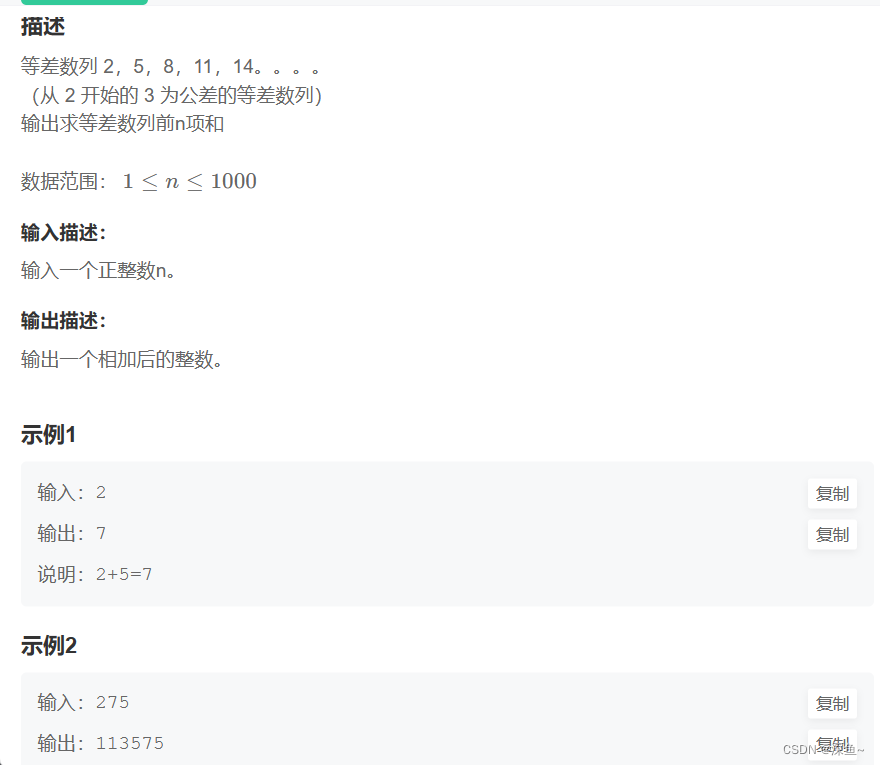
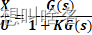题目：

思路：

        根据题意，我们先找到对应的 n 阶台阶的方案数是多少。

        n = 1        f(n) = 1

        n = 2        f(n) = 2

        n = 3        f(n) = 3

        n = 4        f(n) = 5

        n = 5        f(n) = 8

        ......            ......

        n = n        f(n) = f(n - 2) + f(n - 1)

所以通过列出的几个样例，我们可以找到相应的规律，随后递推出公式是：

n = n        f(n) = f(n - 2) + f(n - 1)

因此，我们可以明确 dp[i]   中  i 的含义为 对应 的台阶方案数，记录好 对应的  i 

代码详解如下：

#include <iostream>
#include <cstring>
#include <algorithm>
#include <queue>
#include <unordered_map>
#define endl '\n'
#define int long long
#define YES puts("YES")
#define NO puts("NO")
#define umap unordered_map
#define All(x) (x).begin(),(x).end()
#pragma GCC optimize(3,"Ofast","inline")
#define ___G std::ios::sync_with_stdio(false),cin.tie(0), cout.tie(0)
using namespace std;
const int N = 2e6 + 10,MOD = 10007;

int dp[N];	

int f(int x)
{
	// 如果相应台阶方案数计算过了
	// 直接返回之前计算过的结果
	if(dp[x]) return dp[x] % MOD;
	
	return (dp[x] = f(x - 1) % MOD + f(x - 2) % MOD);
}

inline void solve()
{
	// dp 初始化
	dp[1] = 1;
	dp[2] = 2;
	
	int n;

	cin >> n;
	
	cout << f(n) % MOD << endl;
	
}


signed main()
{
//	freopen("a.txt", "r", stdin);
	___G;
	int _t = 1;
//	cin >> _t;
	while (_t--)
	{
		solve();
	}

	return 0;
}

最后提交：