左手坐标系：DX、3DMax

右手坐标系：OpenGL

世界坐标系、物体坐标系、摄像机坐标系

---

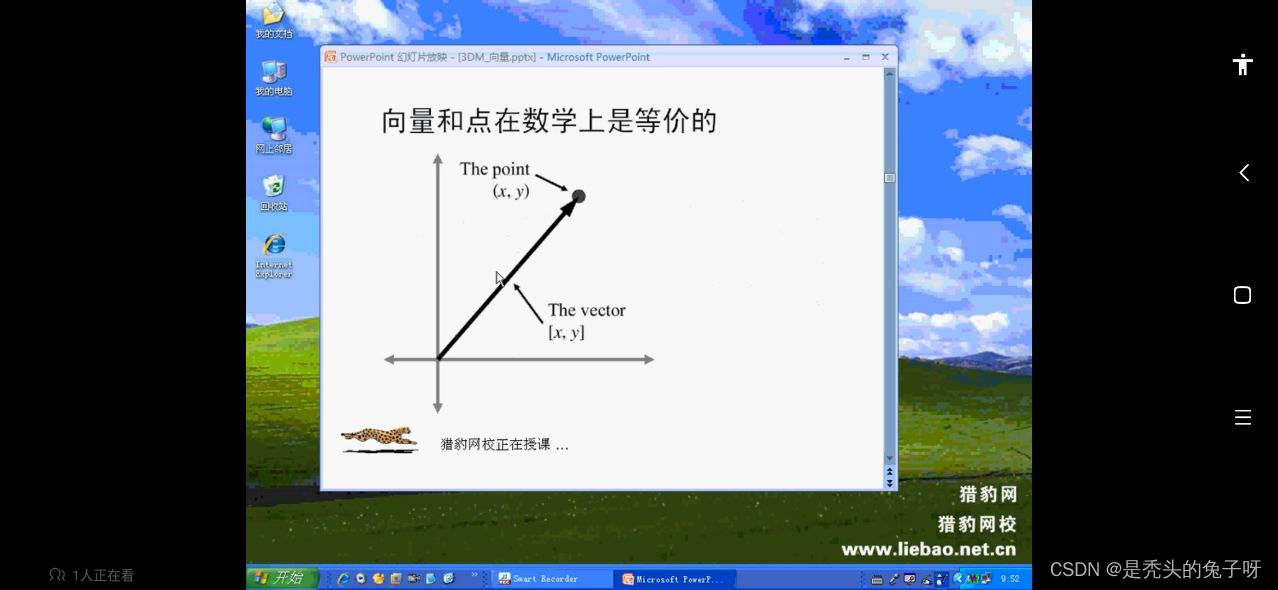
向量和点在数学上是等价的，向量是有大小和方向的有向线段，向量没有位置，只有大小和方向

---

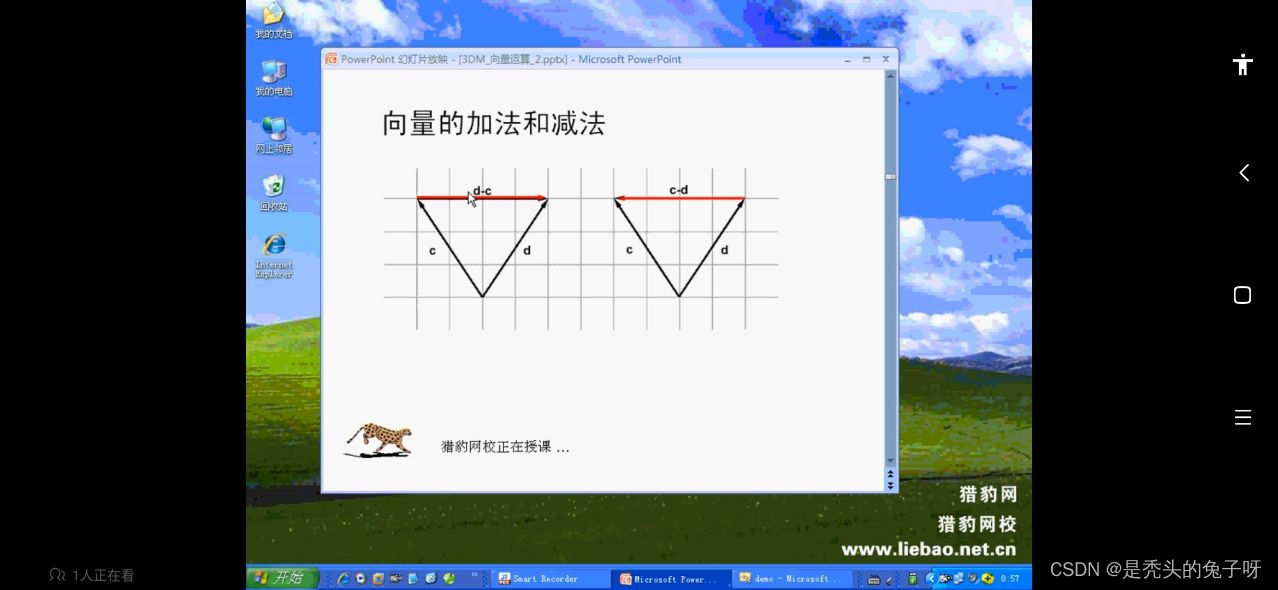
向量运算： 

零向量：[ 0, 0, 0 ] 是唯一一个没有方向的向量

负向量：-[ x, y ] = [ -x, -y ]                

向量大小、长度、模：模(x, y) = sqrt(x² + y²)

标量与向量的乘法：2 * [ x, y ] = [ 2x, 2y ]

单位向量（标准化向量）： [ x, y ] / [ sqrt(x² + y²) ]

向量点乘：a * b = | a | | b | cosx     [ x, y ] * [ a, b ] =  xa + yb

向量叉乘：[ x, y, z ] * [ a ,b, c ] = [ y1z2 - z1y2, z1x2 - x1z2, x1y2 - y1x2 ]

---

矩阵运算：

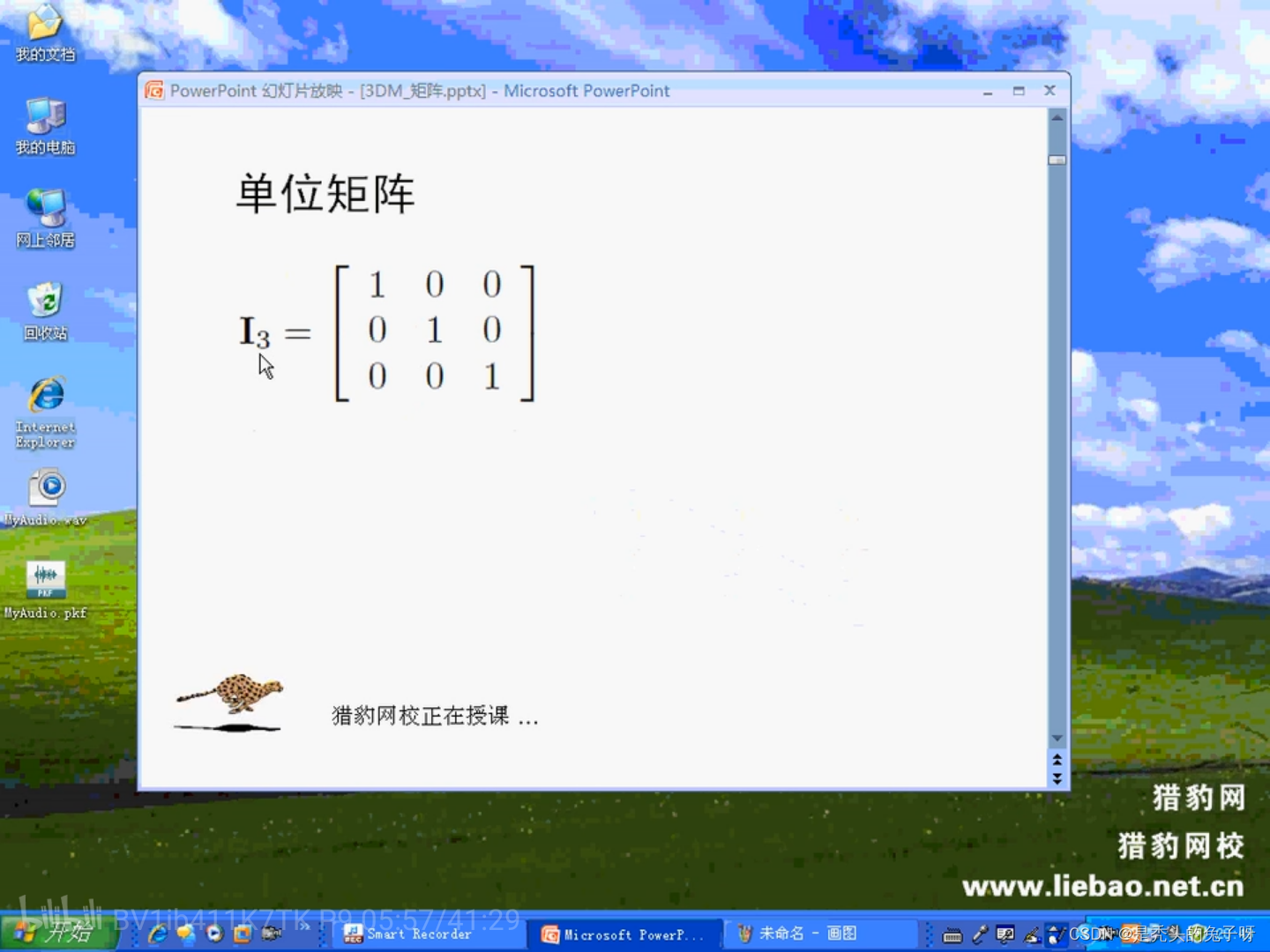
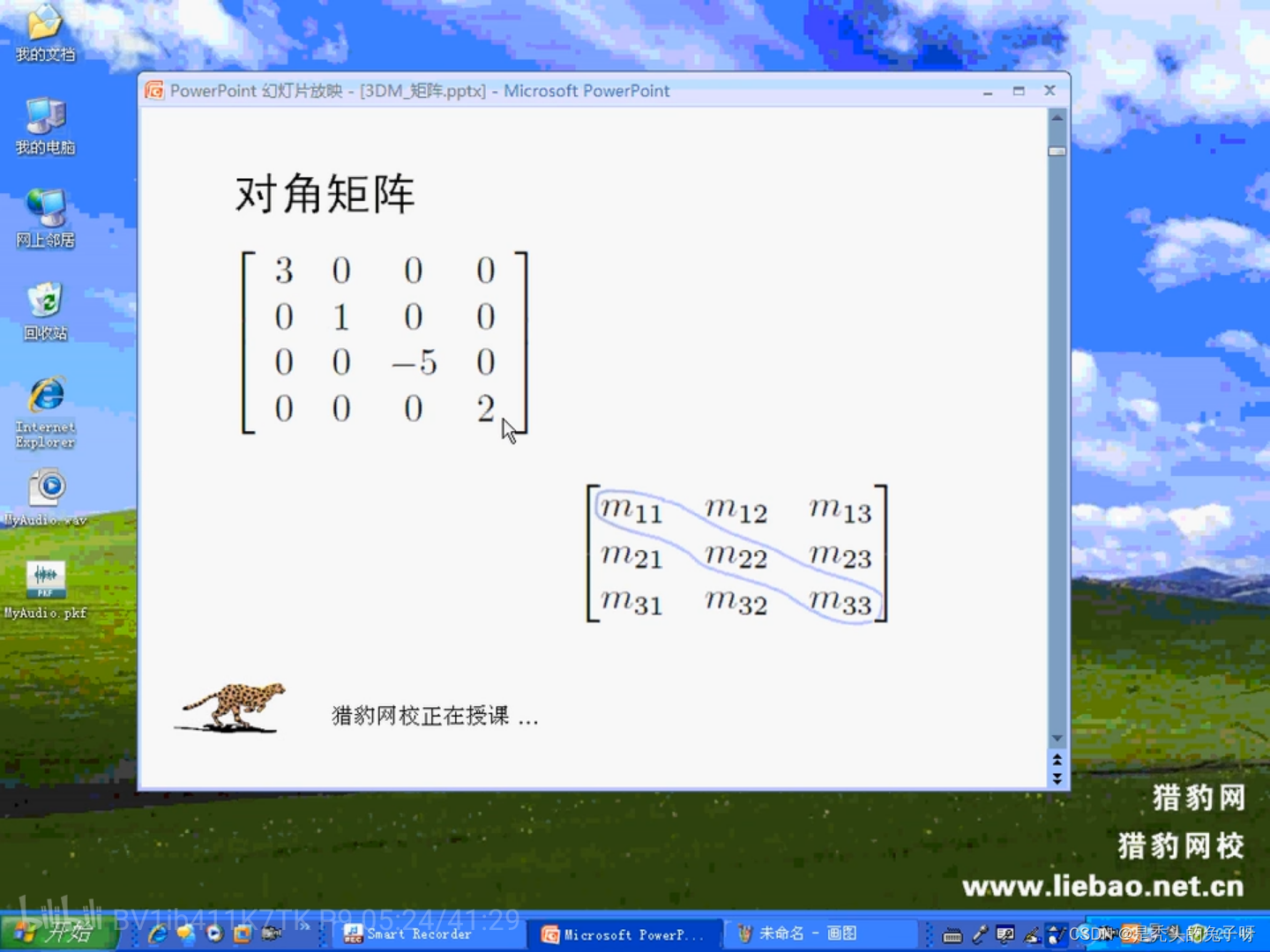
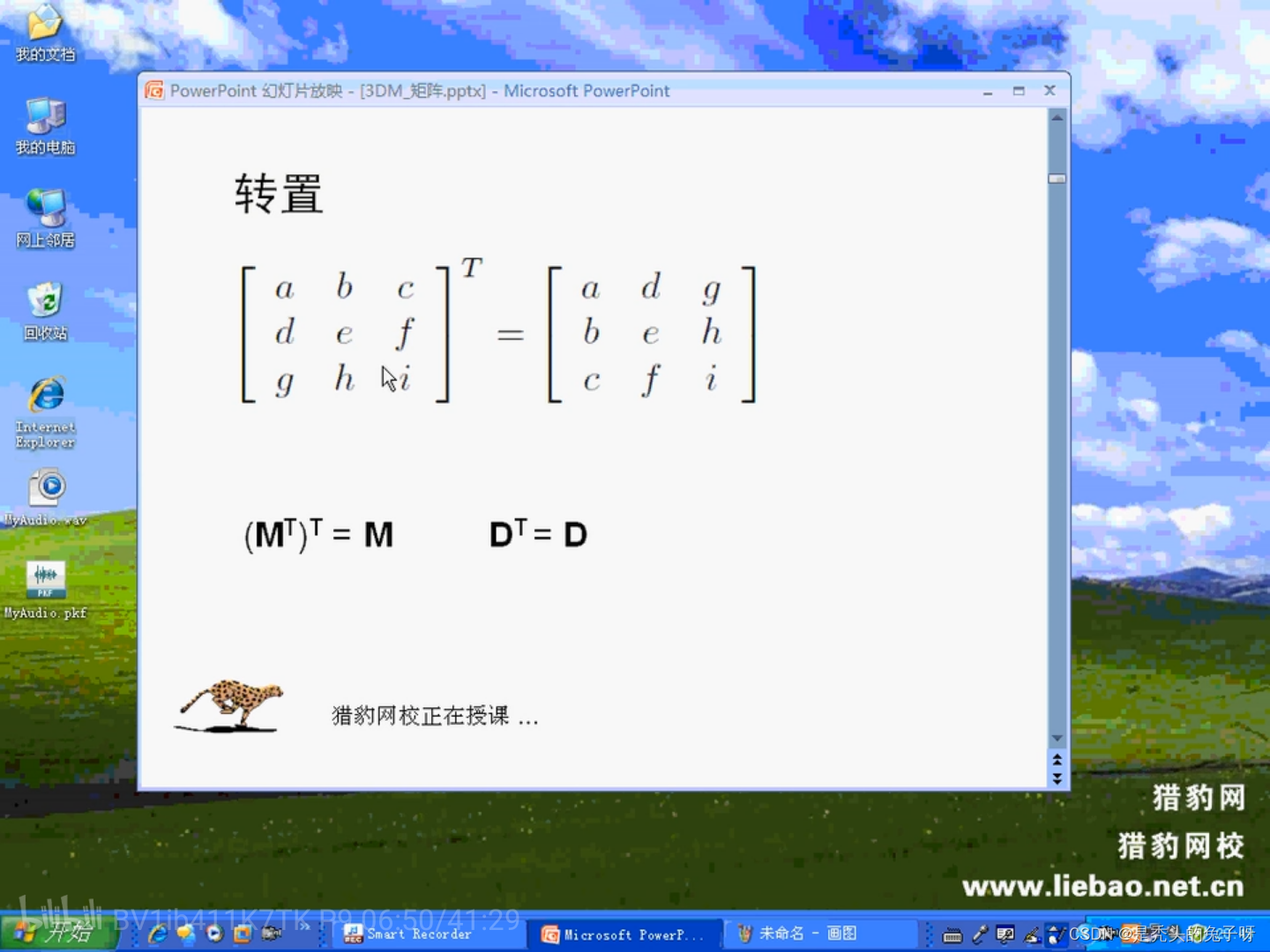
标量与矩阵的乘法：

kM = k * [m11, m12, m13] = [km11, km12, km13]

              [m21, m22, m23]    [km21, km22, km23]

              [m31, m32, m33]    [km31, km32, km33]

矩阵与矩阵的乘法

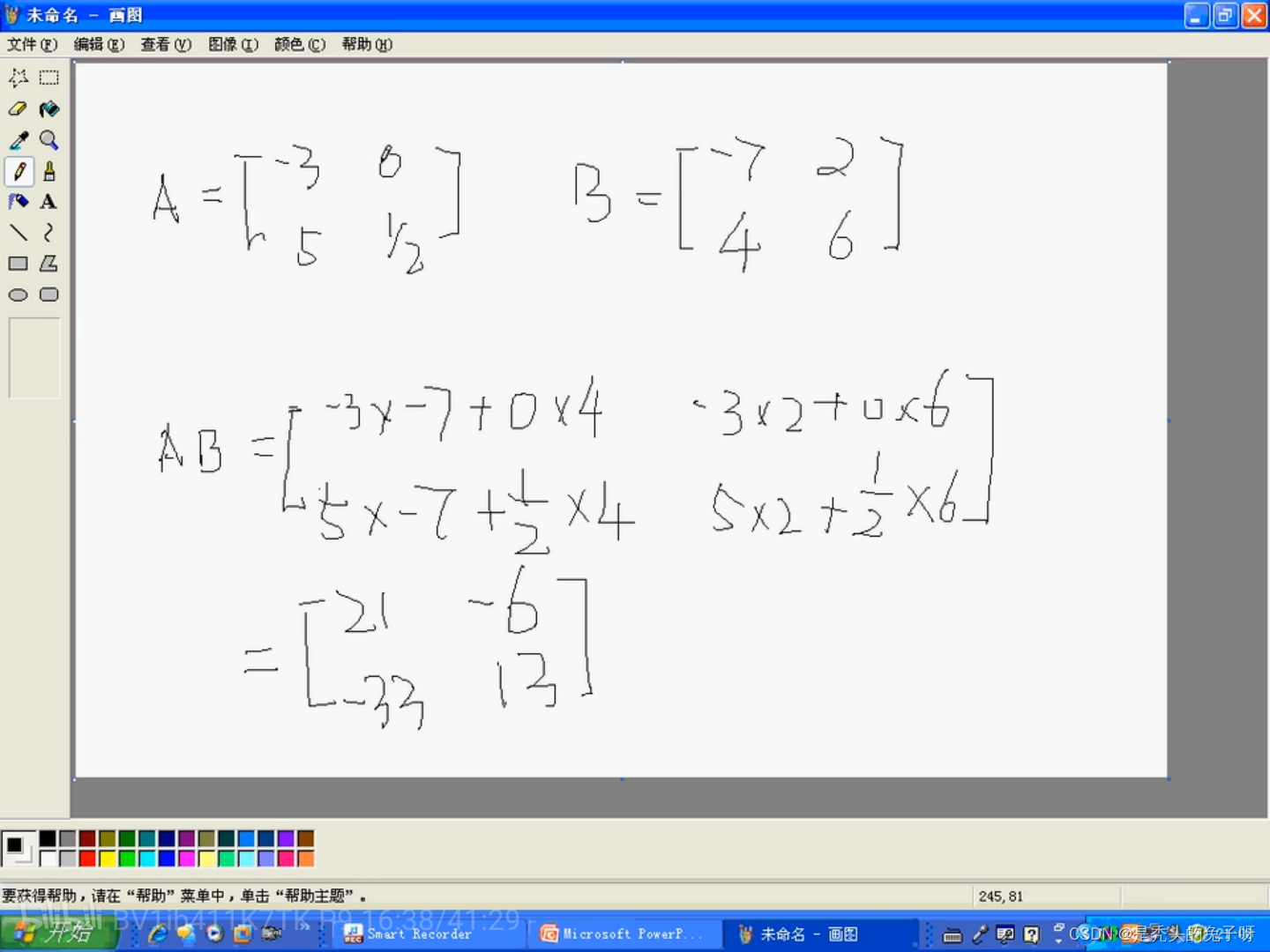
 行对竖对应相乘相加

---

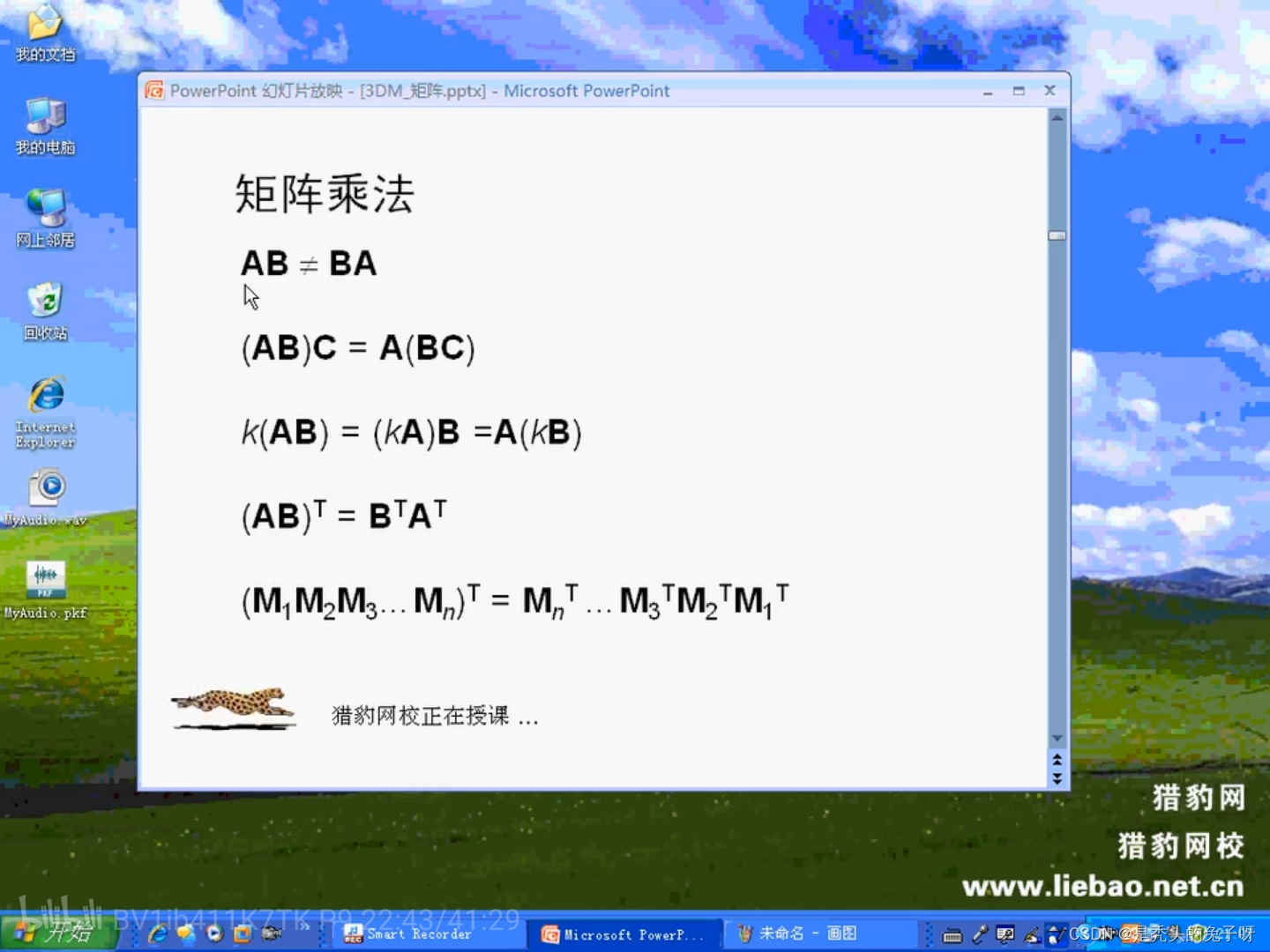
矩阵和线性变换：

1、旋转

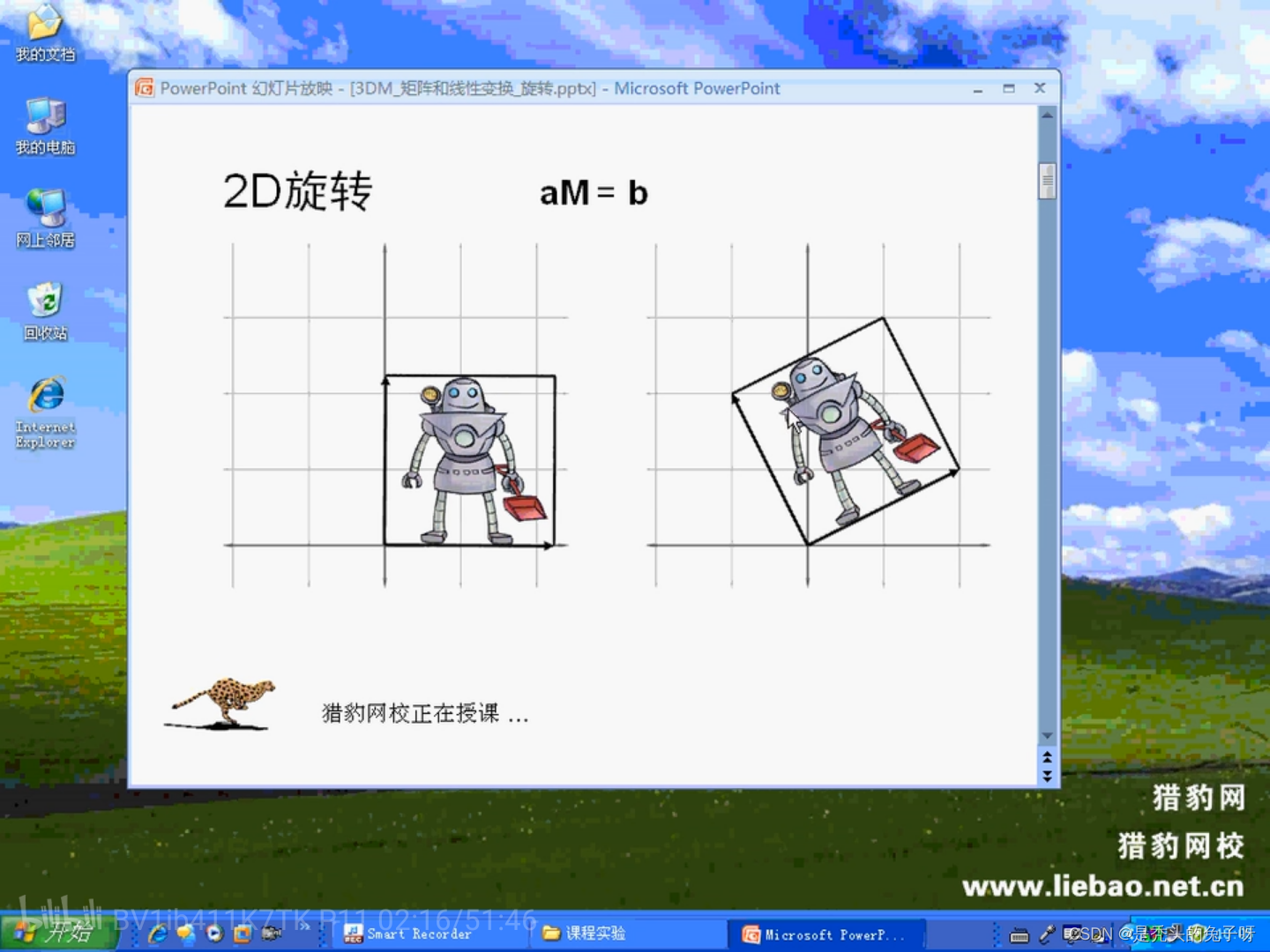
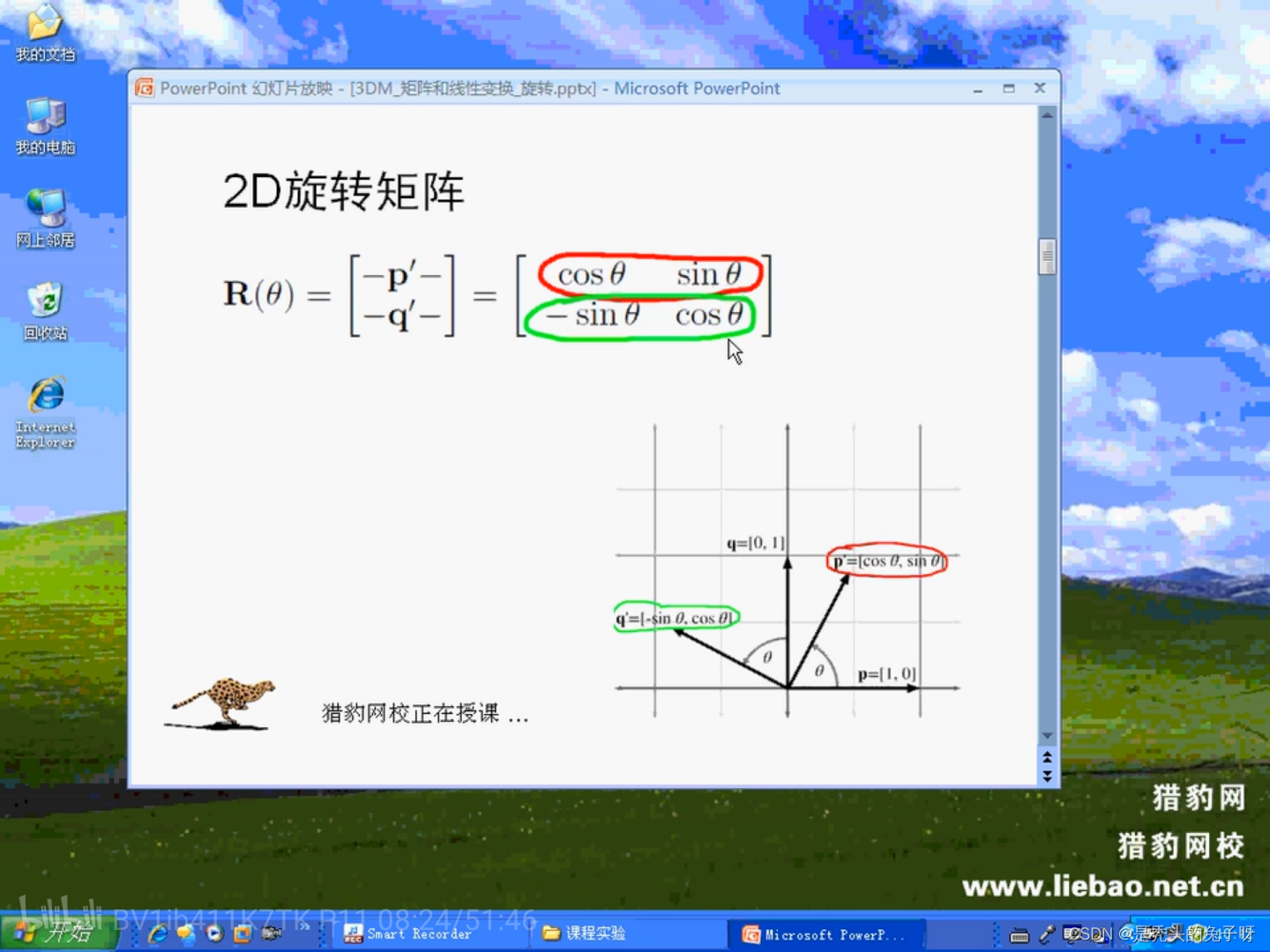
绕X轴进行旋转：

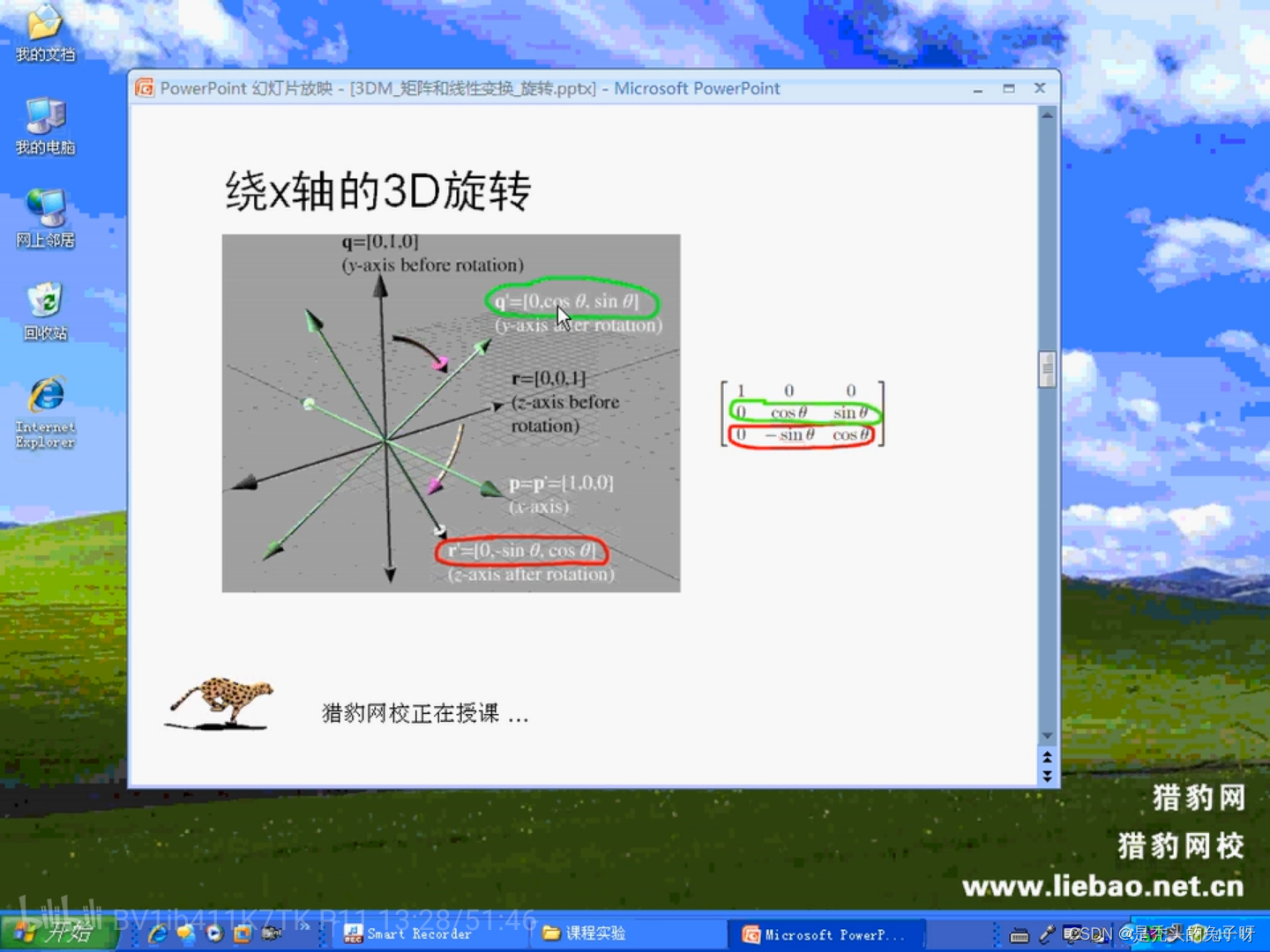
同理：

绕Y轴旋转：

[ COS, , -SIN ]

[ 0, 1, 0 ]

[ SIN, 0, COS ]

绕Z轴旋转：

[ COS, SIN, 0 ]

[ -SIN, COS, 0 ]

[ 0, 0, 1 ]

---

2、缩放

---

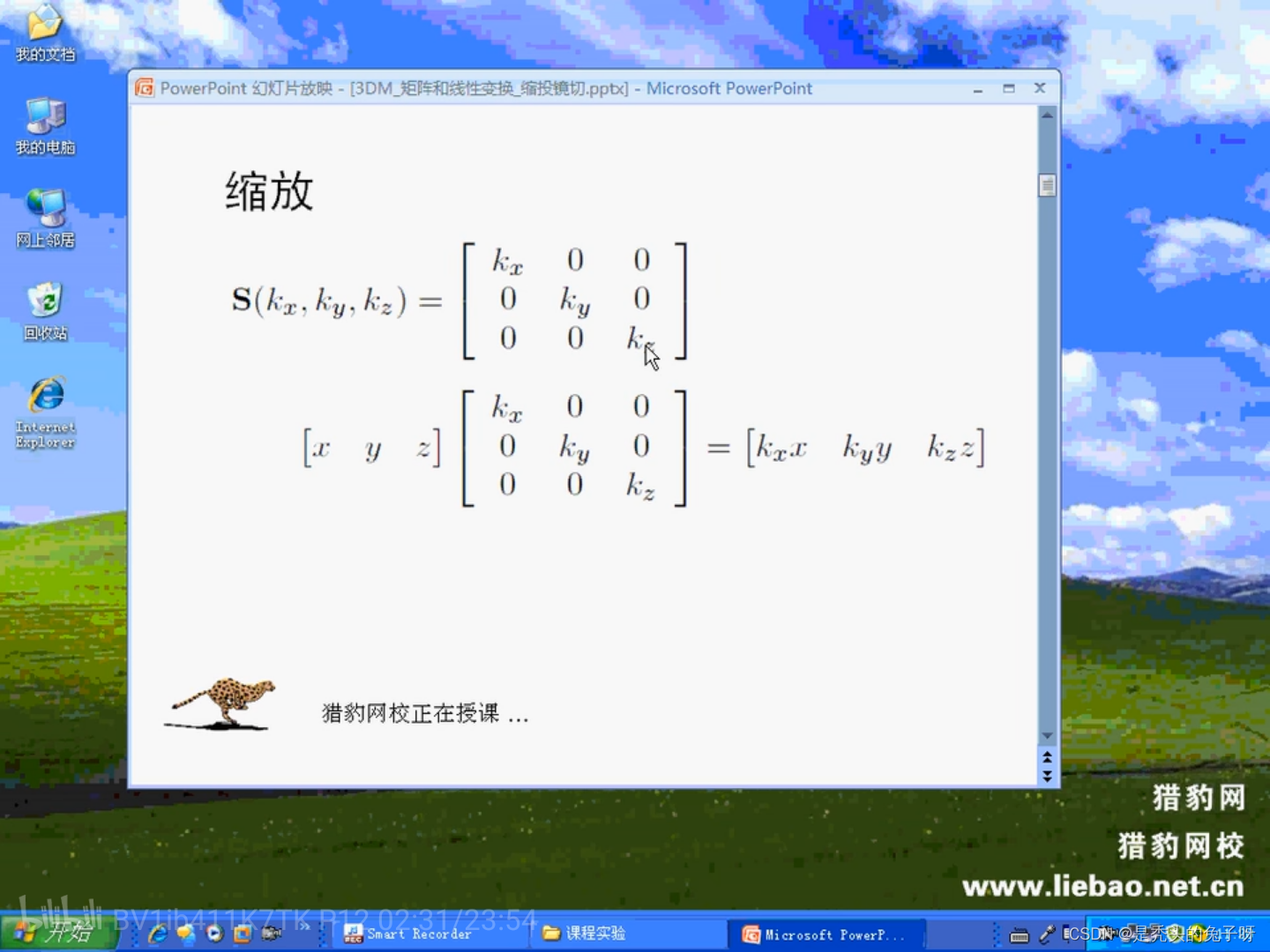
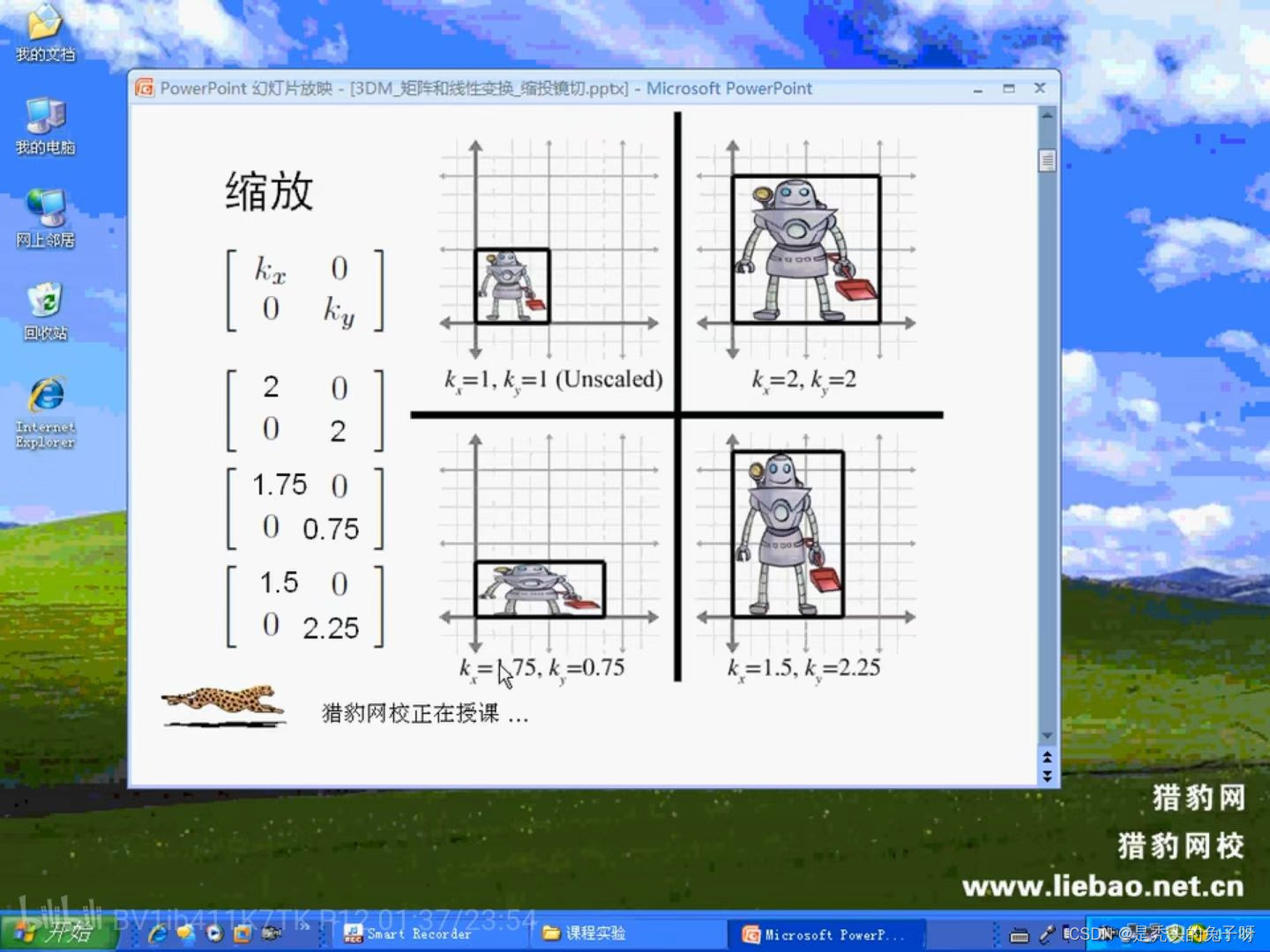
3、投影：

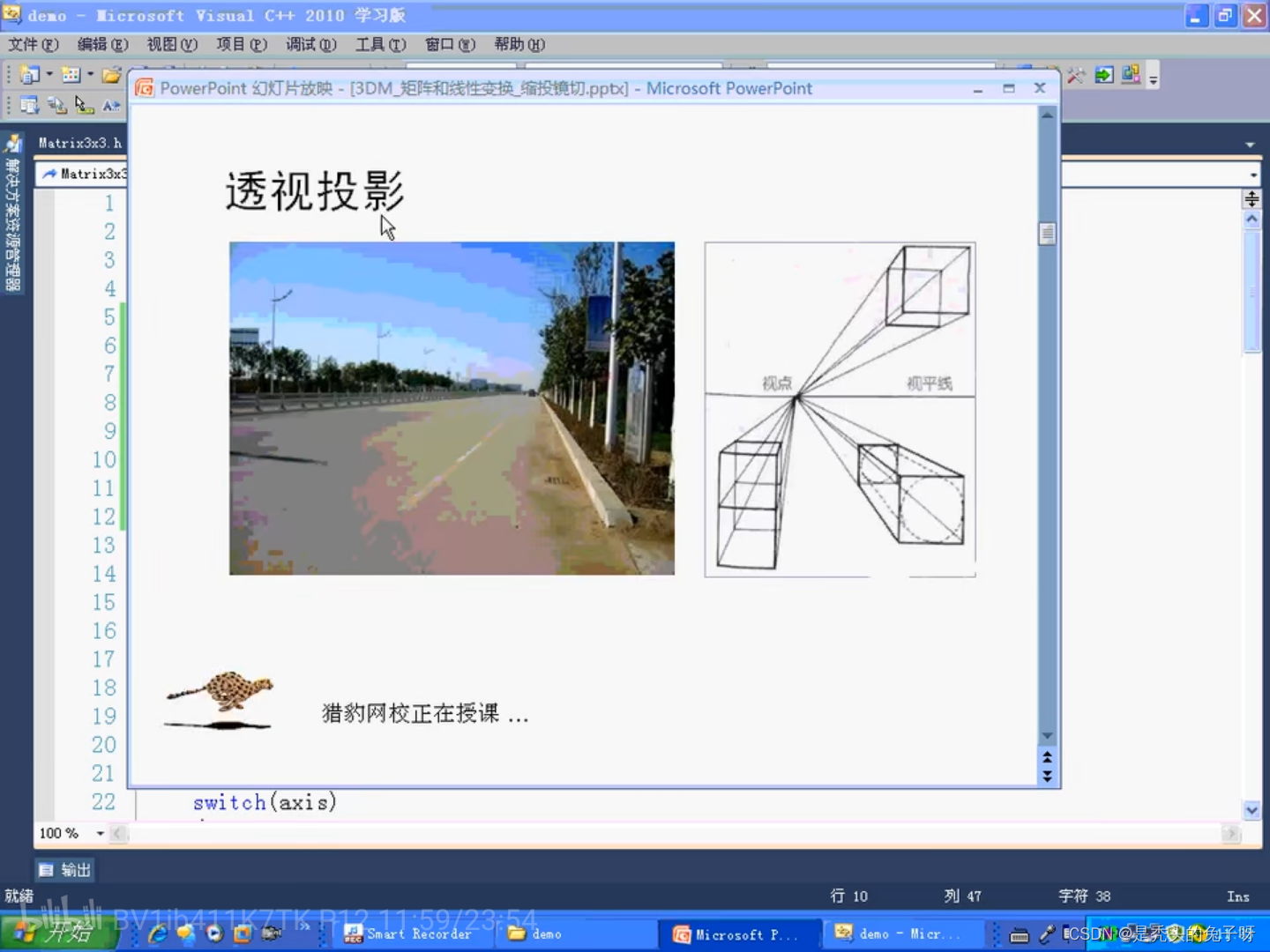
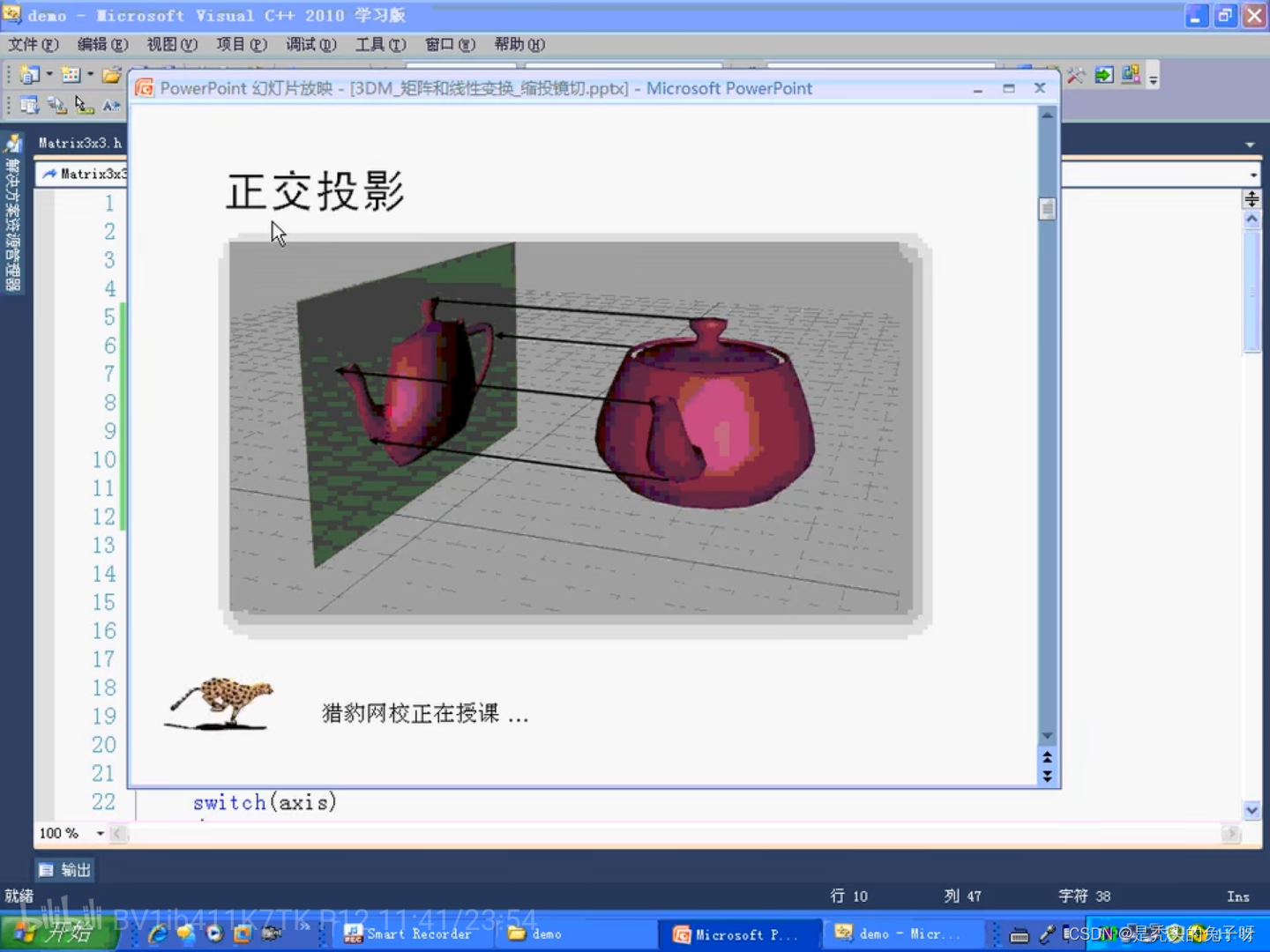
投影的本质就是从三维变成二维

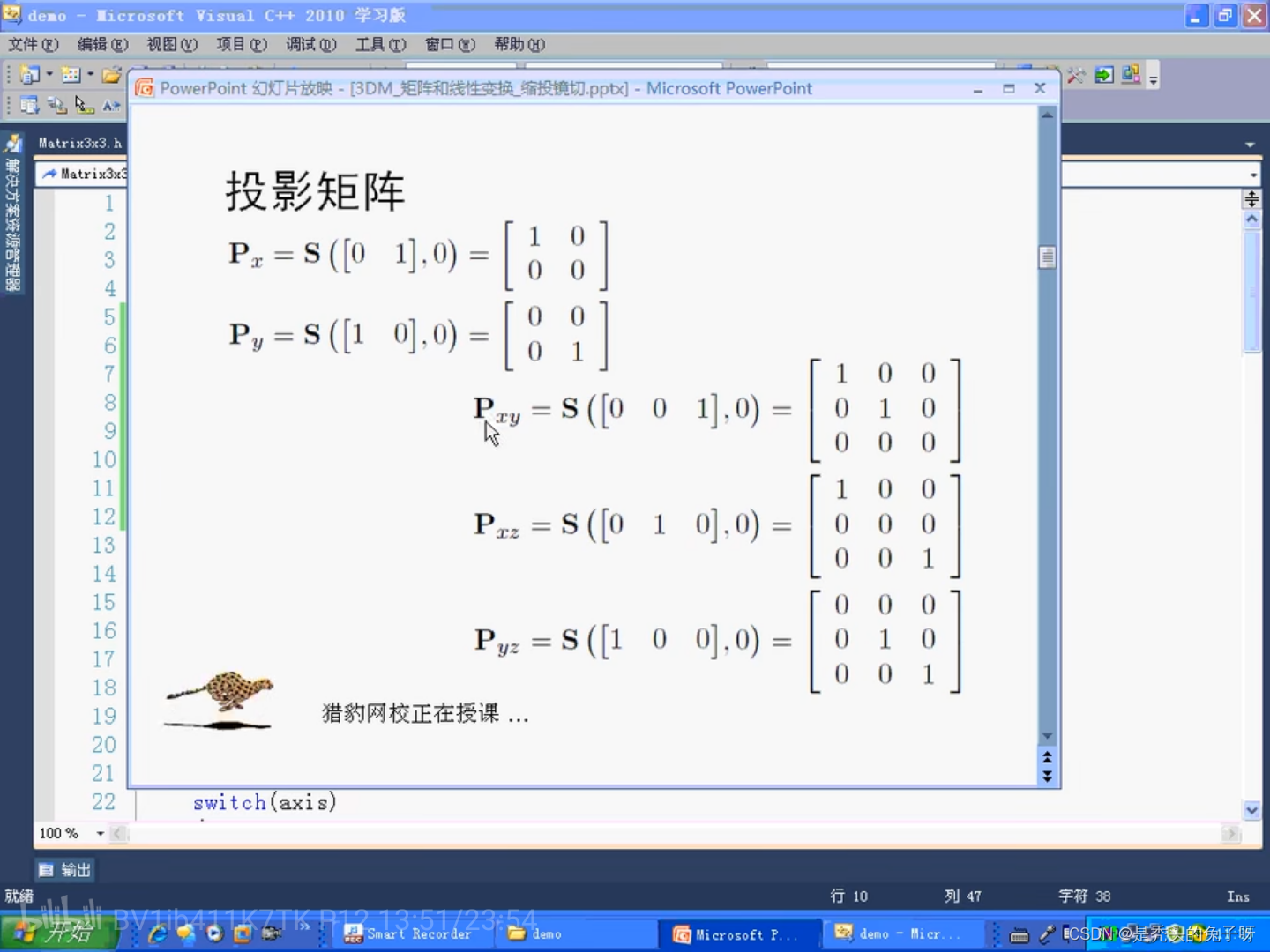
二维Px投影到X轴，其他轴就为0，同理二维投影到Y轴，X轴就全为0

三位投影，投影到XY轴，Z轴就全为0，同理...

---

4、镜像：

---

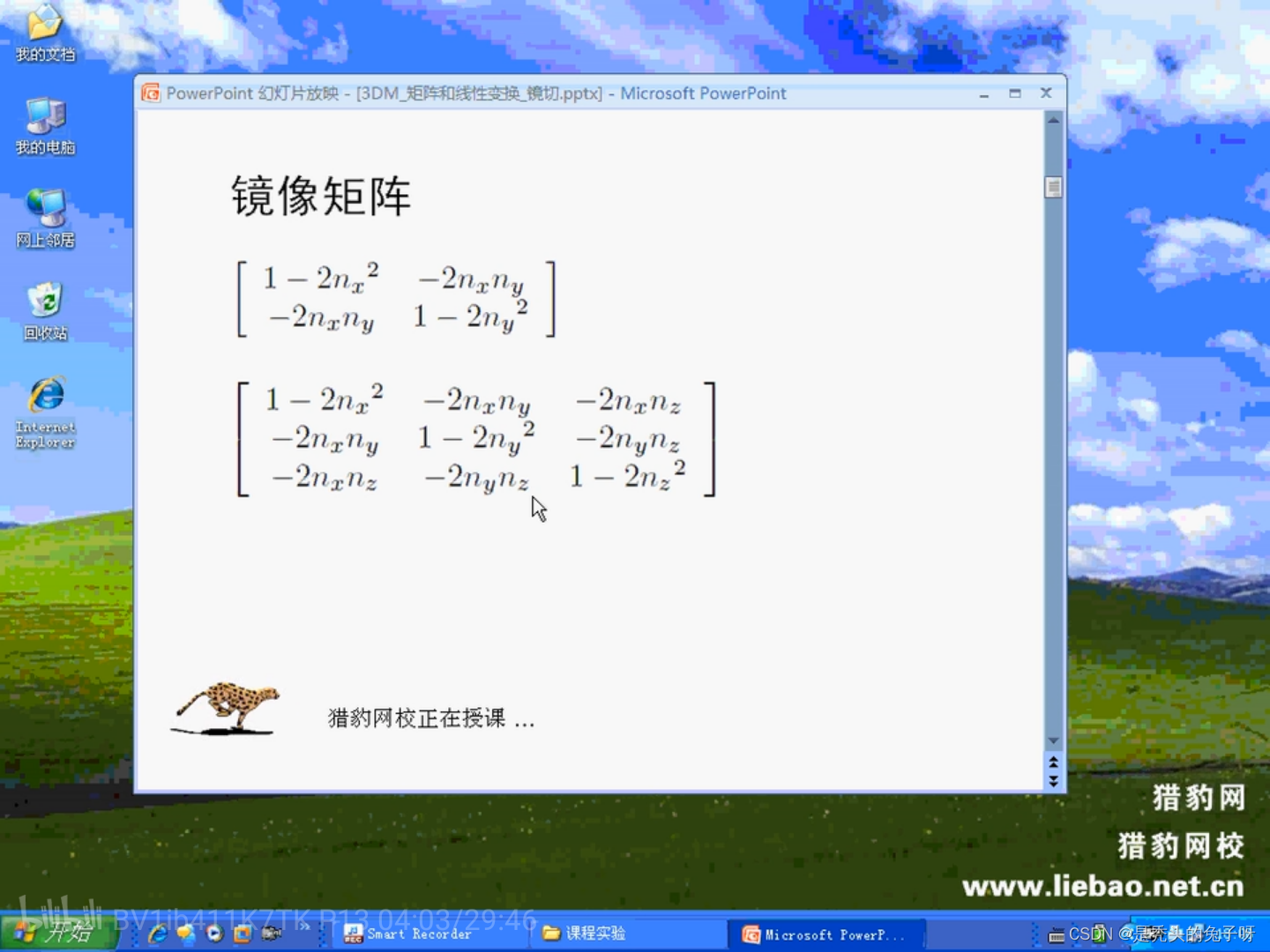
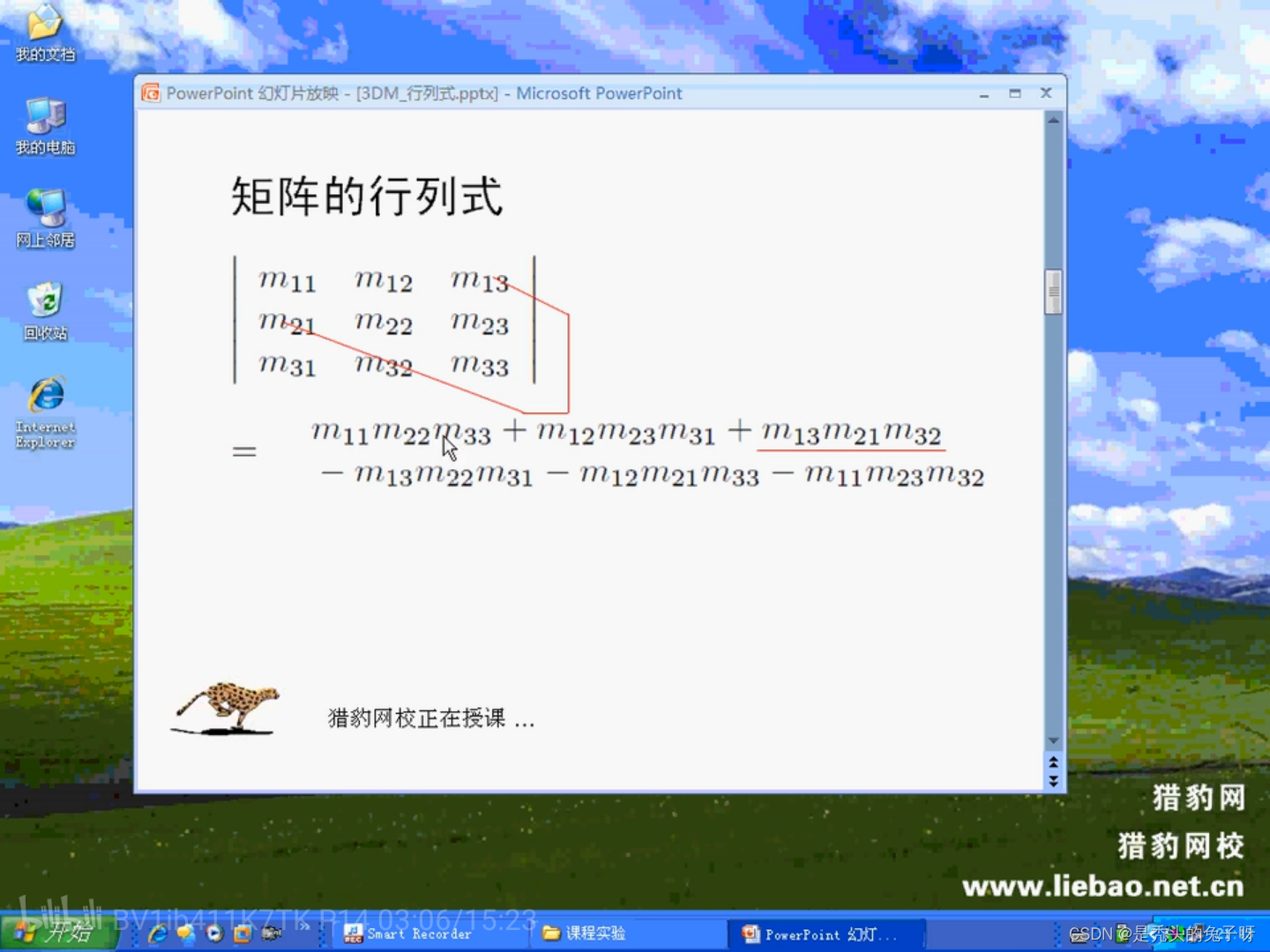
矩阵的行列式：

矩阵只有在方阵中才具有行列式（方阵：行数和列数相同的矩阵） 

---

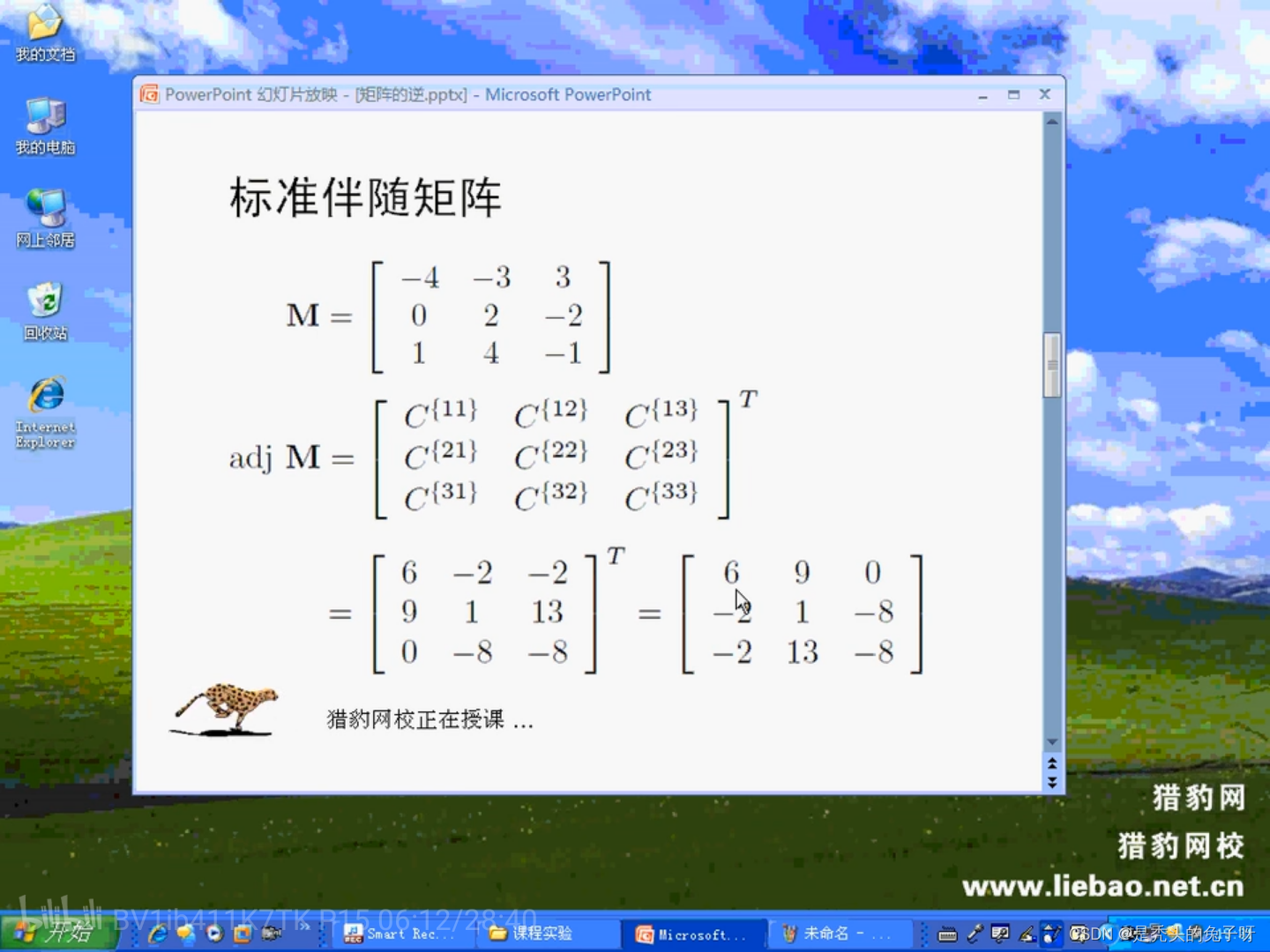
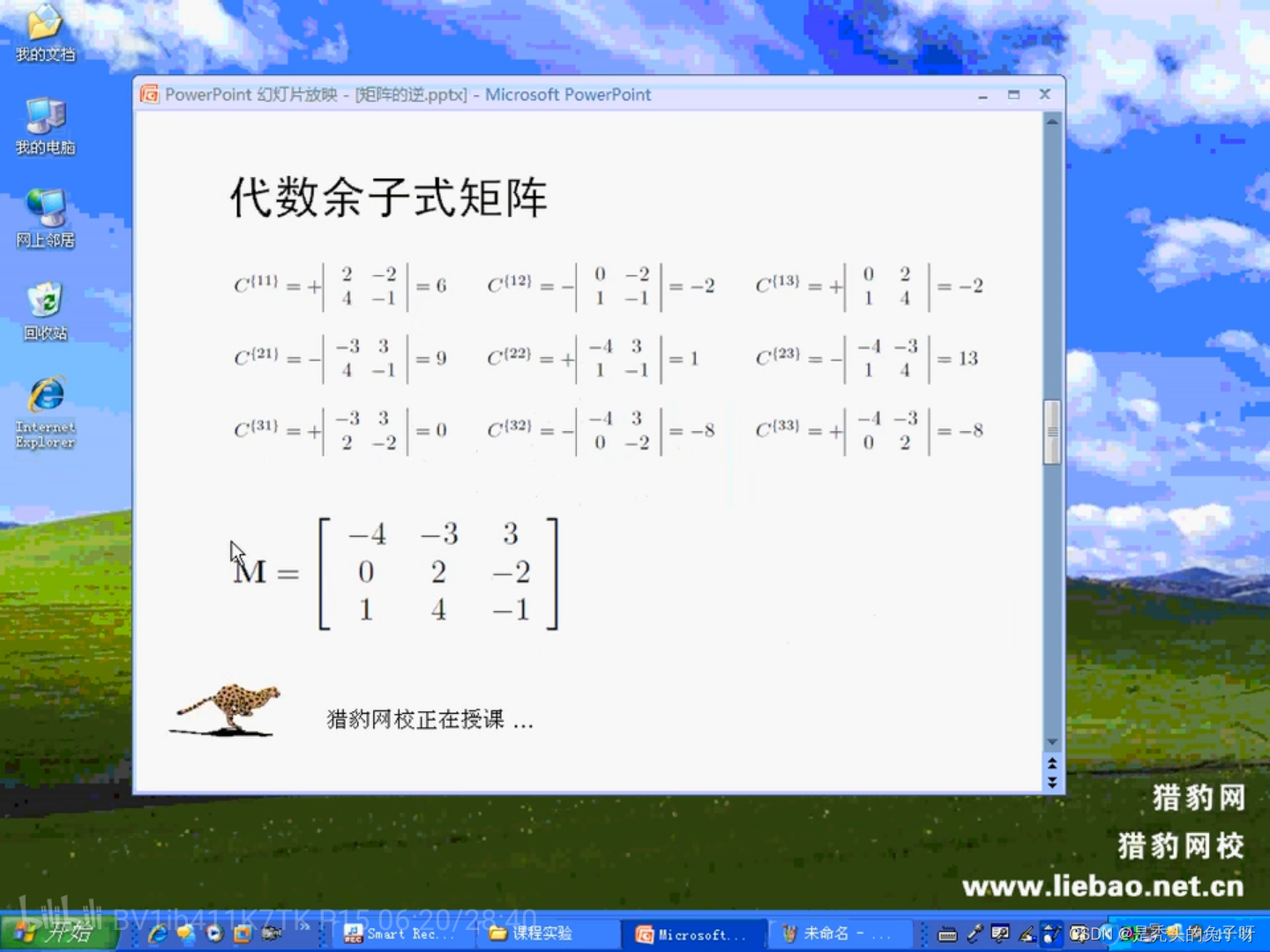
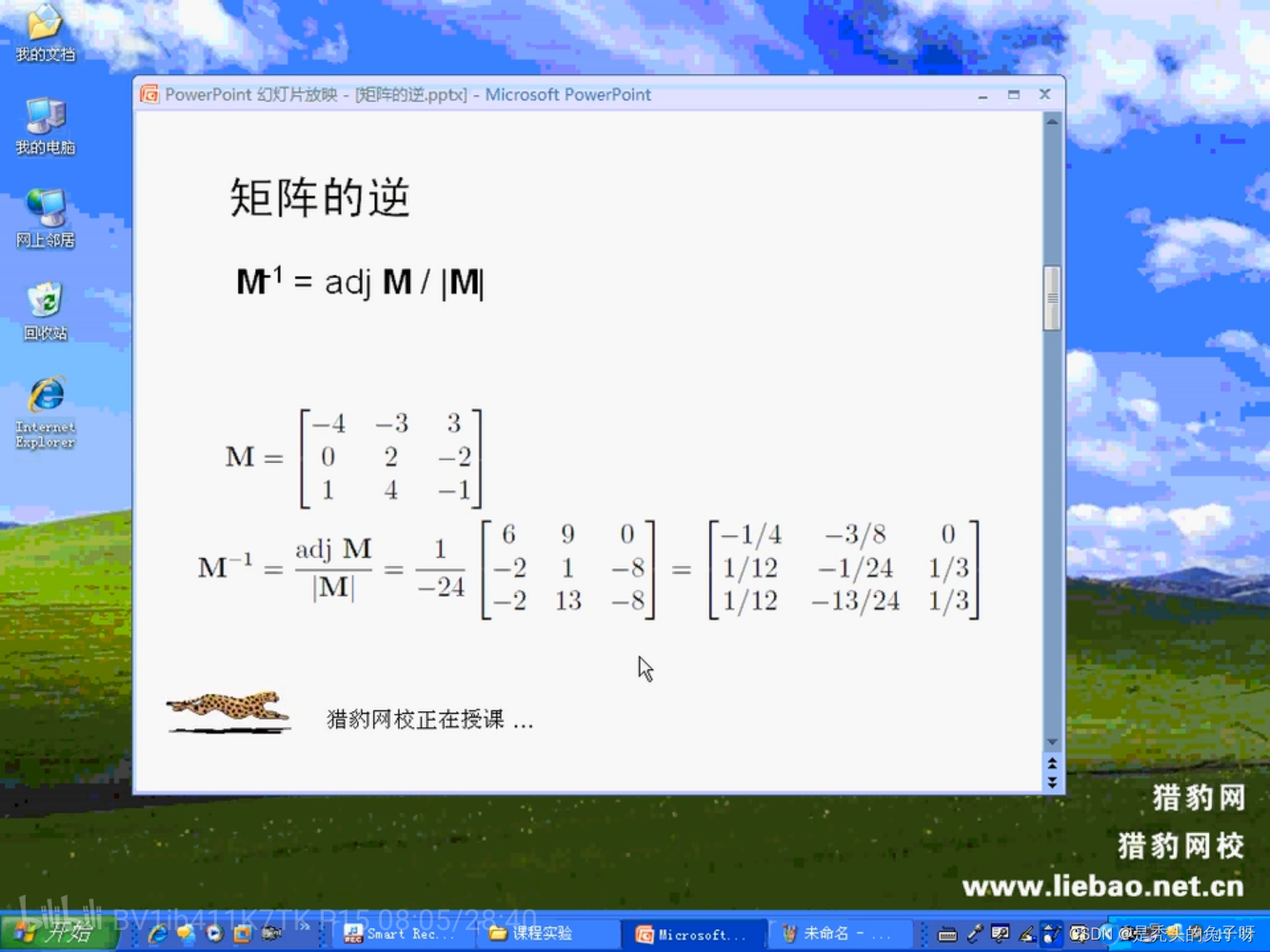
矩阵的逆：

奇异矩阵的行列式为0，奇异矩阵为不可逆矩阵 

---

正交矩阵： 

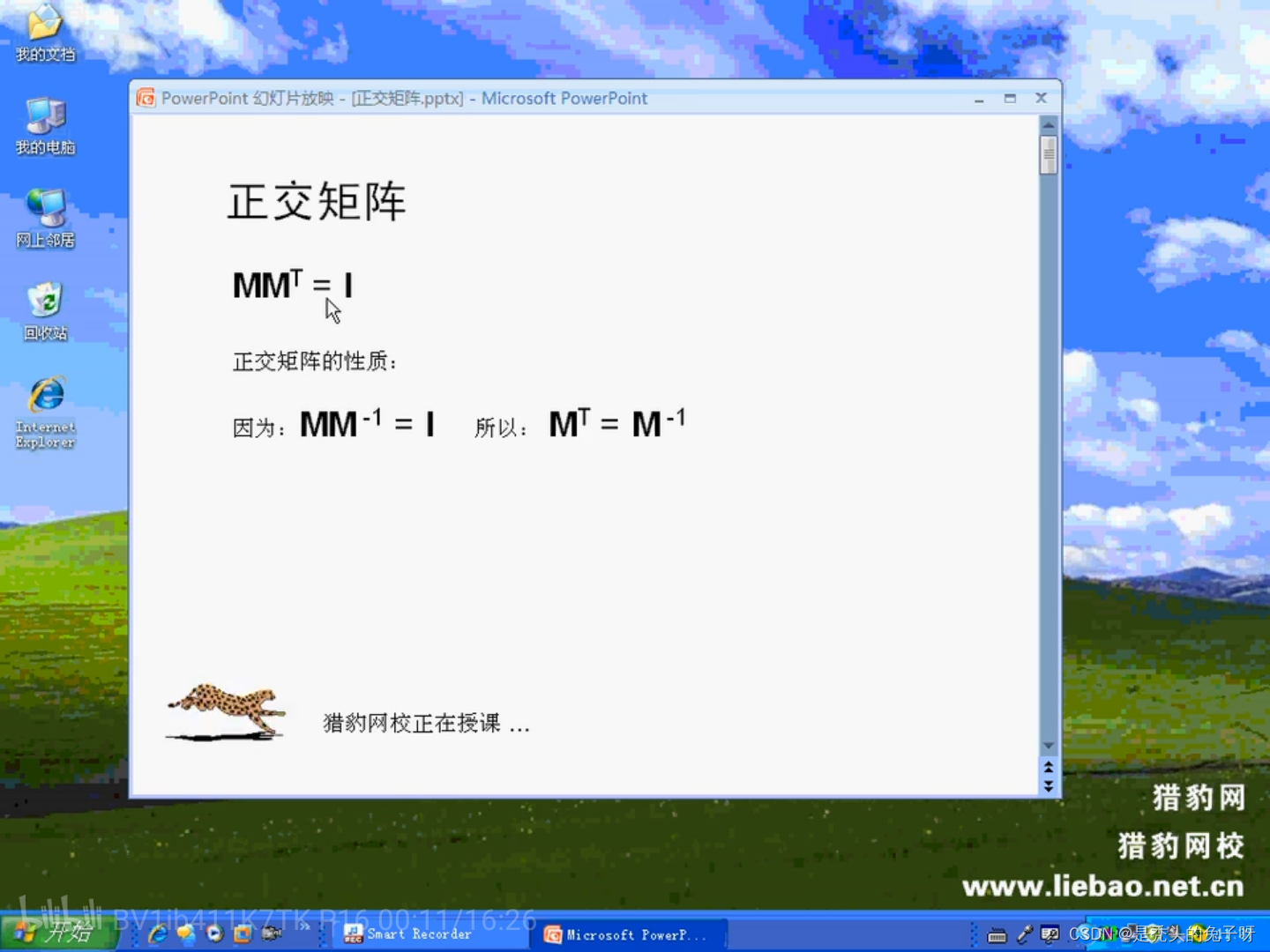
逆矩阵和转置矩阵相同的就是为正交矩阵 

---

4*4齐次矩阵：

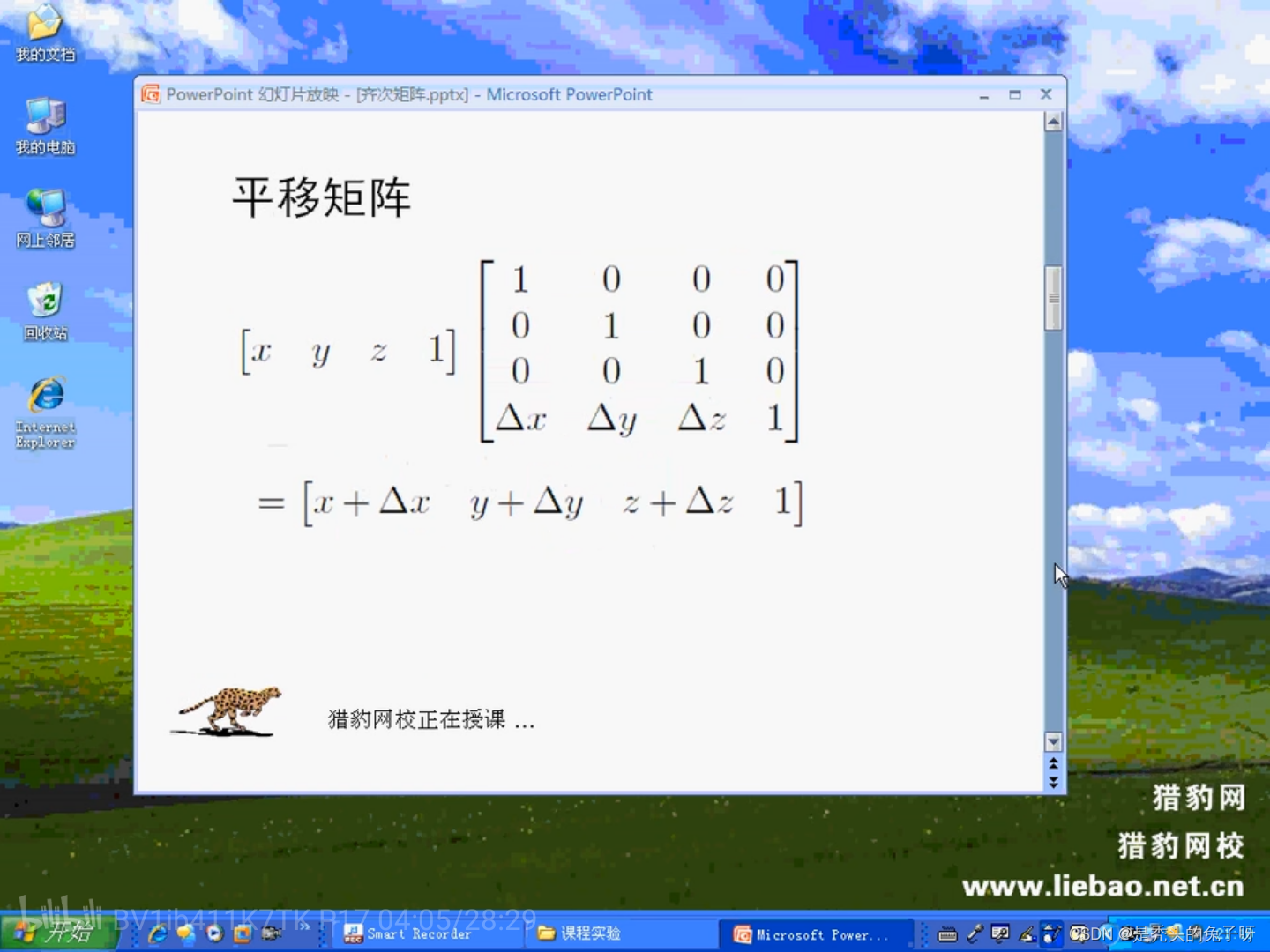
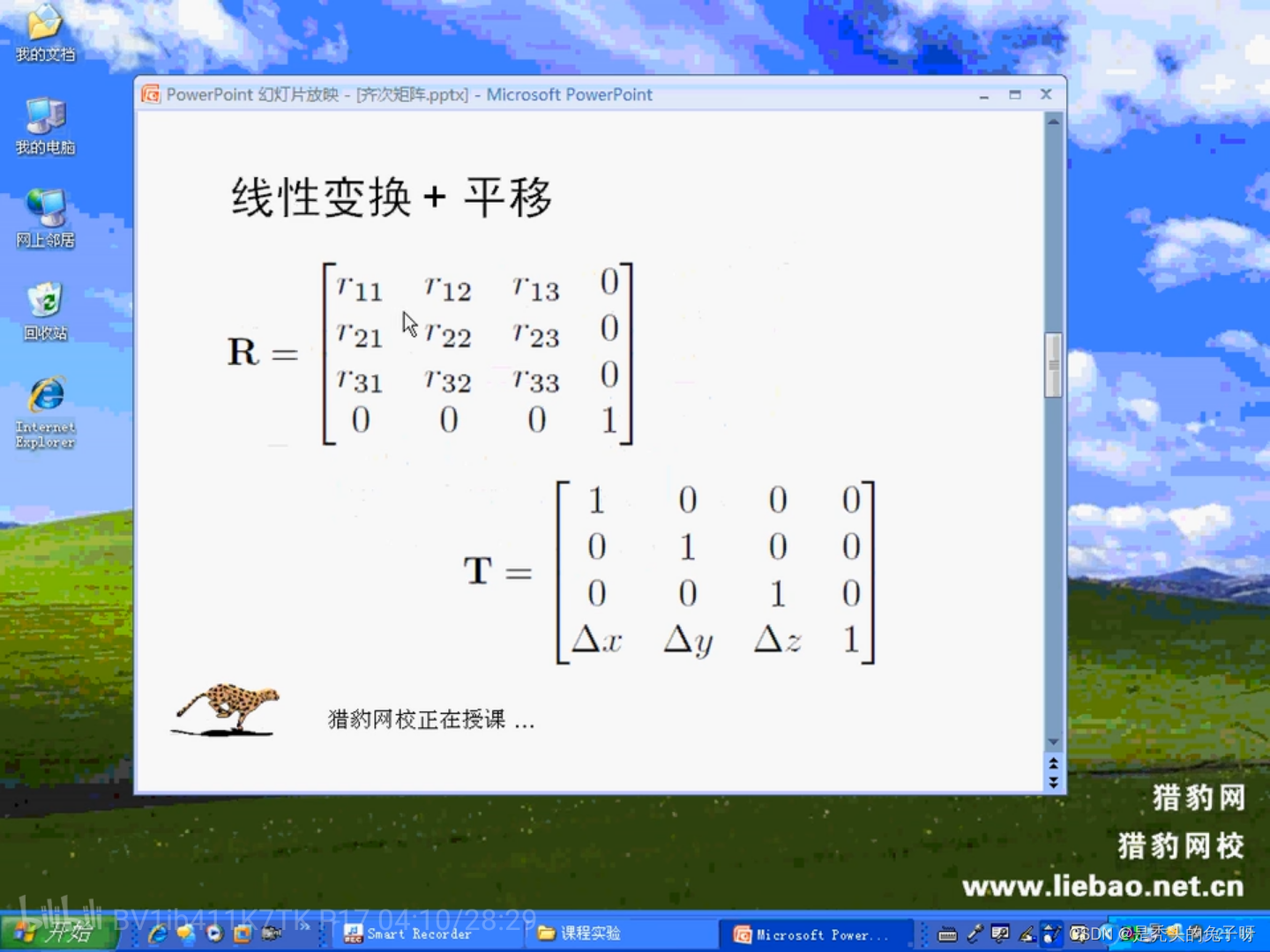
用一个矩阵做变换 + 平移