198.打家劫舍

思路：

题目要求不偷相邻两家，两种偷法，偷法1是偷前k-1间房子，最后一间不偷；偷法2是偷前k-2间房子和最后一间。

代码实现1

class Solution {
    public int rob(int[] nums) {
      
        //偷法1：偷前k-1间房子，最后一间不偷，偷法2：偷前k-2间房子和最后一间
        //dp[k] 对应子问题 f(k)，即偷前 k 间房子的最大金额。
        int[] dp=new int[nums.length+1];
        dp[0]=0;
        dp[1]=nums[0];
        for(int i=2;i<dp.length;i++){
            dp[i]=Math.max(dp[i-1],dp[i-2]+nums[i-1]);

        }
        return dp[nums.length];

    }
}

代码实现2

优化，用一个滚动数组，因为每次比较只会涉及3个值，让这3个值轮回循环就可以了

class Solution {
    public int rob(int[] nums) {
         int pre=0,cur=0,tmp;
        //一直只有这三个(pre,cur,tmp轮换)
        for(int num:nums){
            tmp=cur;
            cur=Math.max(pre+num,cur);
            pre=tmp;
        }
        return cur;

    }
}

213.打家劫舍II

这道题在198基础上增加了"环形",其他地方没变，

k神解法，把环形拆成两个子问题

环状排列 意味着第一个房子和最后一个房子中 只能选择一个偷窃，因此可以把此 环状排列房间 问题约化为两个 单排排列房间 子问题：

1.在不偷窃第一个房子的情况下（即 nums[1:]），最大金额是 p1

2.在不偷窃最后一个房子的情况下（即 nums[:n−1]），最大金额是 p2

综合两种情况要找的是max(p1,p2)。

状态定义：dp[i] 代表前 i个房子在满足条件下的能偷窃到的最高金额。

转移方程：

1.设有n间房子，此时向这些房子后加一间房，此房间价值为num；

2.加一间房子后由于不能抢相邻房子，意味着抢第n+1个房间就不能抢第n间；那么前n+1间房能偷取到的最高金额dp[n+1]一定是一下两种情况下的较大值：

    不抢第n+1个房间，因此等于前n个房子的最高金额，即dp[n+1]=dp[n]

    抢第n+1个房间，此时不能抢第n个房间；因此等于前n-1个房子的最高金额加上当前房间价值，即dp[n+1]=dp[n-1]+num；

初始状态：

• 前 0 间房子的最大偷窃价值为 000 ，即 dp[0]=0

返回值：
  返回 dp列表最后一个元素值，即所有房间的最大偷窃价值。
简化空间复杂度：
  我们发现 dp[n] 只与 dp[n−1] 和 dp[n−2] 有关系，因此我们可以设两个变量 cur和 pre 交替记录，将空间复杂度降到 O(1) 。

代码实现

class Solution {
    public int rob(int[] nums) {
        //分两种情况：1.不偷窃第一个房子(nums[1:],最大金额是p1);2.不偷窃最后一个房子，偷nums[:,n-1],最大金额是p2
        //综合就是要求max(p1,p2)
        if(nums.length==1){return nums[0];}
        return Math.max(myRob(Arrays.copyOfRange(nums,0,nums.length-1)),
        myRob(Arrays.copyOfRange(nums,1,nums.length)));

    }
    //198.题的思路
    int myRob(int[] nums){
        int pre=0,cur=0,tmp;
        //一直只有这三个(pre,cur,tmp轮换)
        for(int num:nums){
            tmp=cur;
            cur=Math.max(pre+num,cur);
            pre=tmp;
        }
        return cur;

    }
}

 337.打家劫舍 III

思路

动态规划其实就是使用状态转移容器来记录状态的变化，可以使用一个长度为2的数组，记录当前节点偷与不偷所得到的的最大金钱。

1.确定递归函数的参数和返回值

返回值是数组，参数是节点

2.确定终止条件

在遍历的过程中，如果遇到空节点的话，很明显，无论偷还是不偷都是0，所以就返回

3.确定遍历顺序

首先明确的是使用后序遍历。 因为要通过递归函数的返回值来做下一步计算。

通过递归左节点，得到左节点偷与不偷的金钱。

通过递归右节点，得到右节点偷与不偷的金钱。

4.确定单层递归的逻辑

如果是偷当前节点，那么左右孩子就不能偷，val1 = cur->val + left[0] + right[0]; （如果对下标含义不理解就再回顾一下dp数组的含义）

如果不偷当前节点，那么左右孩子就可以偷，至于到底偷不偷一定是选一个最大的，所以：val2 = max(left[0], left[1]) + max(right[0], right[1]);

5.举例推导dp数组

用后序遍历的方式推导

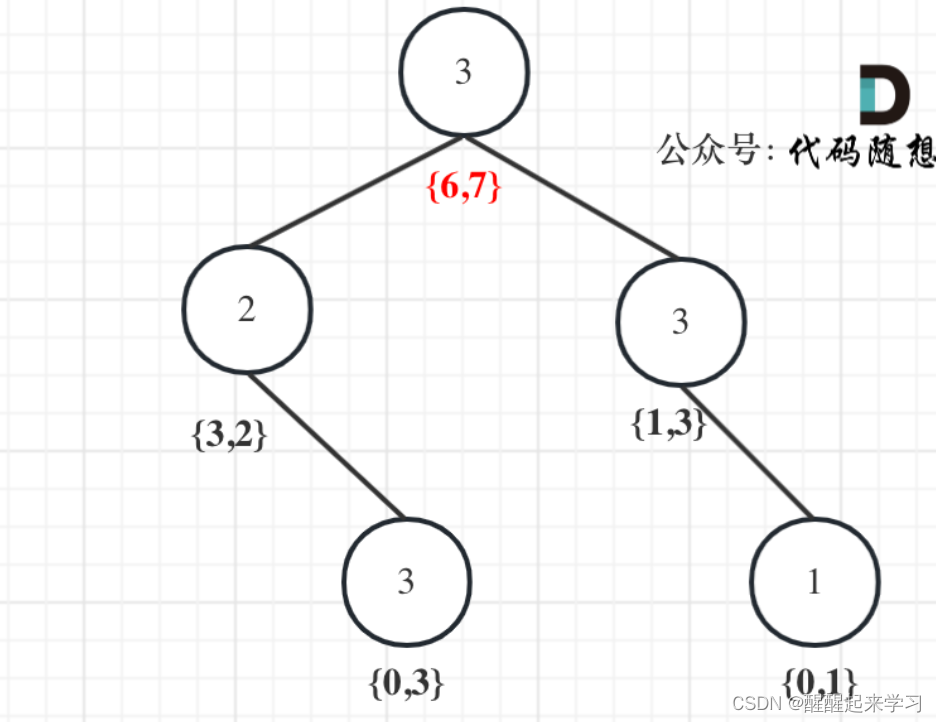
最后头结点就是 取下标0 和 下标1的最大值就是偷得的最大金钱。

 3.状态标记递归
    // 执行用时：0 ms , 在所有 Java 提交中击败了 100% 的用户
    // 不偷：Max(左孩子不偷，左孩子偷) + Max(又孩子不偷，右孩子偷)
    // root[0] = Math.max(rob(root.left)[0], rob(root.left)[1]) +
    // Math.max(rob(root.right)[0], rob(root.right)[1])
    // 偷：左孩子不偷+ 右孩子不偷 + 当前节点偷
    // root[1] = rob(root.left)[0] + rob(root.right)[0] + root.val;

代码实现 

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public int rob(TreeNode root) {
        //广度优先搜索
        int[] res=dfs(root);
        return Math.max(res[0],res[1]);


    }

    int[] dfs(TreeNode root){
        int[] res=new int[2];//res[0]:偷当前节点，res[1]不偷当前节点
        //终止条件
        if(root==null){return res ;}
        //遍历节点顺序
        int[] left= dfs(root.left);//遍历左节点，存储左节点偷，不偷的情况
        int[] right=dfs(root.right);
        /**
        res[0]=root.val+left[0]+right[0];
        res[1]=Math.max(left[0],left[1])+Math.max(right[0],right[1]);
         */
        //不偷当前节点，左右孩子不偷
        res[1]=root.val+left[0]+right[0];
        //偷当前节点,考虑偷左还是
        res[0]=Math.max(left[0],left[1])+Math.max(right[0],right[1]);

        
        return res;


    }
}