属性
归并排序(MERGE-SORT)是建立在归并操作上的一种有效的排序算法,该算法是采用分治法(Divide and Conquer)的一个非常典型的应用。将已有序的子序列合并,得到完全有序的序列;即先使每个子序列有序,再使 子序列段间有序。若将两个有序表合并成一个有序表,称为二路归并。 归并排序核心步骤:
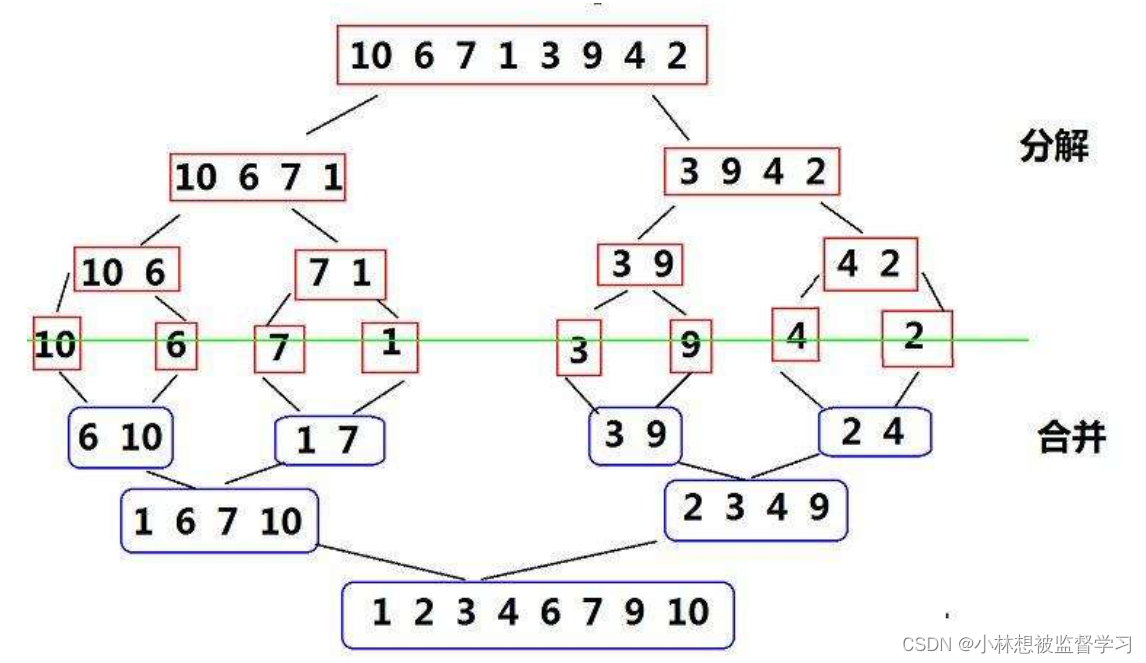 归并排序总结
归并排序总结
1. 归并的缺点在于需要O(N)的空间复杂度,归并排序的思考更多的是解决在磁盘中的外排序问题。
2. 时间复杂度:O(N*logN)
3. 空间复杂度:O(N)
4. 稳定性:稳定
代码及注释(递归实现)
//mergeSort是归并排序提供使用的方法
public static void mergeSort(int[]arr){
//用mergeSortChild进行递归排序
mergeSortChild(arr,0,arr.length-1);
}
private static void mergeSortChild(int[]arr,int left,int right){
//出递归
if(left>=right){
return;
}
//先计算出要排序数据的中间位置
int mid=(left+right)/2;
//先分别归并排序左边和右边的数据,排序好以后再将左边和右边的数据合并
mergeSortChild(arr,left,mid);
mergeSortChild(arr,mid+1,right);
merge(arr,left,right);
}
private static void merge(int[]arr,int left,int right){
int mid=(left+right)/2;
//left和right范围的数据分为了两个部分
//用s1,e1表示第一部分的数据范围,s2,e2表示第二部分的数据范围
//两个部分的数据分别是排序好了的,要将两个部分的数据进行合并
int s1=left;
int e1=mid;
int s2=mid+1;
int e2=right;
//定义辅助数组help来帮助合并
int[]help=new int[right-left+1];
//放数据的时候有以下的几种情况
//1.两个部分的数据还没有哪个部分全放到help数组中
int k=0; //k是用于指向help数组的下标
while (s1<=e1&&s2<=e2){
//当s1下标的数据比s2下标的小时,s1下标的数据就先放到help数组中
if(arr[s1]<arr[s2]){
help[k++]=arr[s1++];
}
else {
help[k++]=arr[s2++];
}
}
//2.s1>e1 第一部分的数据都放到了help数组中
//直接将第二部分的数据全放到help数组中
while (s2<=e2){
help[k++]=arr[s2++];
}
//3.s2>e1 第二部分的数据都放到了help数组中
//直接将第一部分的数据全放到help数组中
while (s1<=e1){
help[k++]=arr[s1++];
}
//此时两个部分的数据都放到了help数组中
//将数组中对应部分的数据改为help数组中的数据(help数组中的数据是合并好了的)
for(int i=left,j=0;i<=right;i++,j++){
arr[i]=help[j];
}
}代码及注释(非递归实现)
//归并排序---非递归
public static void mergeSortNo(int[] array){
//一个数据为一组
int gap=1;
while (gap<array.length){
for(int i=0;i<array.length;i+=2*gap){
int left=i;
int mid=left+gap-1;
int right=mid+gap;
merge(array,left,mid,right);
}
gap=gap*2;
}
}
//合并
private static void merge(int[] array,int left,int mid,int right){
int s1=left;
int e1=mid;
int s2=mid+1;
int e2=right;
//定义辅助数组
int[]help=new int[right-left+1];
int k=0;
//两组数据都没放完
while (s1<=e1&&s2<=e2){
if(array[s1]<array[s2]){
help[k++]=array[s1++];
}
else {
help[k++]=array[s2++];
}
}
//当有一组中的数据放完
while (s1<=e1){
help[k++]=array[s1++];
}
while (s2<=e2){
help[k++]=array[s2++];
}
//将合并好的数据返回给数组array
for (int i=0;i<help.length;i++){
array[left+i]=help[i];
}
}



![[Hadoop] start-dfs.sh ssh报错](https://img-blog.csdnimg.cn/a2b48d2c570447caab9cbb723814c886.png)