一、前言

这个LSTM系列是在学习时间序列预测过程中的一些学习笔记，包含理论分析和源码实现两部分。本质属于进阶内容，因此神经网络的基础内容不做过多讲解，想学习基础，可看之前的神经网络入门系列文章：

https://blog.csdn.net/yangwohenmai1/category_9126892.html?spm=1001.2014.3001.5482https://blog.csdn.net/yangwohenmai1/category_9126892.html?spm=1001.2014.3001.5482

本系列重心放在解析LSTM算法逻辑、前向和反向传播数学原理、推导过程、以及LSTM模型的源码实现上。本文详细讲解了LSTM源码的实现过程，以及数据在LSTM网络中流转的全过程，尽量做到每一行代码都讲解清楚，即是自己对知识做总结，也方便大家学习。本文是建立在前两篇文章的基础上，很多数学表达式不在重新推导，详细过程可查阅本系列第一篇和第二篇文章。

二、前情回顾

阅读本文前务必要先看上一篇文章，上篇文章讲解了LSTM网络的前向传播流程，本文接着上篇文章继续讲解LSTM网络的反向传播流程，用到的数据和变量均为上一篇文章的延续，所以要结合上篇文章才能看懂本文：

LSTM内部结构及前向传播原理——LSTM从零实现系列(1)_量化交易领域专家YangZongxian的博客-CSDN博客LSTM前向传播原理https://forecast.blog.csdn.net/article/details/127958263?spm=1001.2014.3001.5502LSTM反向传播原理——LSTM从零实现系列(2)_量化交易领域专家YangZongxian的博客-CSDN博客lstm反向传播原理https://forecast.blog.csdn.net/article/details/128047225?spm=1001.2014.3001.5502

LSTM前向传播代码实现——LSTM从零实现系列(3)_量化交易领域专家YangZongxian的博客-CSDN博客lstm前向传播代码实现https://forecast.blog.csdn.net/article/details/128154254?spm=1001.2014.3001.5502

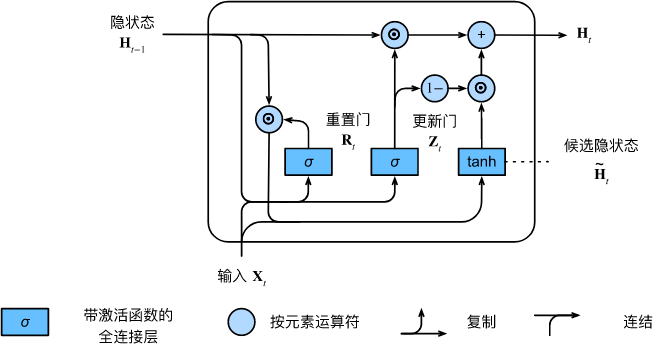
开始讲解反向传播之前，再来回顾一下这篇文章的模型结构，如下图所示：

三、损失函数

关于损失函数，上篇文章我们已经描述过代码如何实现，本模型用的是[softmax+二元交叉熵]的组合，反向传播时softmax损失函数的求导过程比较复杂，之前的文章里已经详细讲解过，可以直接参看下面给出的连接：

手动推导softmax神经网络反向传播求导过程——softmax前世今生系列(6)_量化交易领域专家YangZongxian的博客-CSDN博客导读：softmax的前世今生系列是作者在学习NLP神经网络时，以softmax层为何能对文本进行分类、预测等问题为入手点，顺藤摸瓜进行的一系列研究学习。其中包含：1.softmax函数的正推原理，softmax的代数和几何意义，softmax为什么能用作分类预测，softmax链式求导的过程。2.从数学的角度上研究了神经网络为什么能通过反向传播来训练网络的原理。3.结合信息熵理论...https://forecast.blog.csdn.net/article/details/96741328 损失函数和SoftMax反向传播的结果会首先传递到[全连接层]中，所以下面我们就从全连接层为起点讲解反向传播的代码实现。

四、全连接层的反向传播代码实现

4.1.误差矩阵的方向传播

下面代码中的self.deltaOri就是上篇文章中损失函数回传的误差矩阵deltaOri.shape(32, 2)，w是全连接层在前向传播过程中所使用的权重矩阵w.shape(30, 2)。

从代码中可以看出，误差矩阵在全连接层的反向传播其实是进行了一次矩阵乘法运算，即仿射变换。即误差矩阵deltaOri与全连接层的权重矩阵w的转置矩阵w.T进行相乘：

deltaOri.shape(32, 2) * w.T.shape(2, 30) => newdeltaOri.shape(32, 30)

完成仿射变换后，将新的误差结果向LSTM继续反向传播。

仿射变换后调整数据的维度：(32,30)=>(32,1,30)

# 误差矩阵反向传播
def bpDelta(self):
    # 将通过激活函数求导后的误差矩阵deltaOri，和当前FCNN层的权重矩阵转置w.T相乘，来将误差向前传播
    deltaPrevReshapped = Tools.matmul(self.deltaOri, self.w.T)
    # 误差矩阵恢复之前Flatten()的拉伸变形，适配上层网络shape以便向上层网络继续反向传播
    self.deltaPrev = deltaPrevReshapped if self.needReshape is False else deltaPrevReshapped.reshape(self.shapeOfOriIn)
    return self.deltaPrev

4.2.权重矩阵参数的更新

计算得到新的误差矩阵后，还要对全连接层的权重矩阵和偏置项进行更新，这里使用的更新函数是getUpdWeights((w, b),(dw, db), lrt)。

dw.shape(30,2)=inputReshaped.T.(30,32)*deltaOri.shape(32,2)

db.shape(2,)=sum((32,2),axis=0)

首先将当前的权重矩阵(w, b)和(dw, db)传入getUpdWeights，使用Adam优化器进行梯度更新，也就是更新[全连接层]中的权重矩阵w.shape(, )和偏置项b.shape(,)的参数。

# 计算反向传播权重梯度w,b
def bpWeights(self, input, lrt):
    # dw = Tools.matmul(input.T, self.deltaOri)
    # inputReshaped是正向传播时上层网络传到本层的输入矩阵，deltaOri是本层反向传播激活函数求导后的误差矩阵
    dw = Tools.matmul(self.inputReshaped.T, self.deltaOri)
    # 误差矩阵deltaOri.shape->(32,10),进行sum计算后将32个sample向量对应位置求和后db.shape->(1,10)，再reshape成b.shape用于后续梯度优化
    db = np.sum(self.deltaOri, axis=0, keepdims=True).reshape(self.b.shape)
    # 当前层网络权重(w,b)元组
    weight = (self.w,self.b)
    # 反向传播的权重(dw,db)元组
    dweight = (dw,db)
    # 元组按引用对象传递，值在方法内部已被更新
    # 将两个元组代入优化器，求出梯度方向，根据梯度更新参数，更新了self.lstmParams[i][Wx,Wh,b]的权重矩阵
    self.optimizerObj.getUpdWeights(weight,dweight, lrt)

五、LSTM层的反向传播代码实现

本文最核心的就是LSTM层的反向传播代码实现部分，由上一节可知全连接层传回的误差矩阵是deltaOri.shape(32,1,30)。

3层LSTM反向传播的代码中包含两个for循环，第一个for循环控制3个LSTM层之间的反向传播计算，每一个LSTM层中包含32个sample；第二个for循环控制每一个sample中包含的T个时间步，之间的反向传播计算。需要说明的是这32个sample的计算时并行进行的。即当计算第一个时间步时，是将32个sample的第一个时间步T1一起传入计算。

5.1.层间循环

在每个LSTM层计算前，首先要重新初始化C参数为零矩阵，作为状态参数传入；同时传入的还有前向传播过程中产生的中间参数cache[]；还要传入一个最重要的参数dh，dh在第一个LSTM层反向传播时传入的是上个FNN层计算得到的误差矩阵，后续的LSTM层反向传播时传入的dh其实是上一个LSTM层的最后一个时间步的输出dx。

第二个for循环内每次输出参数列举如下：

dx：反向传播到输入x位置的误差，每个时间步的计算结果按时间步维度保存，作为下个LSTM层的状态输入dh
dh：反向传播到输入状态h位置的误差，这个值在每层LSTM循环完全结束后会被抛弃，本质是计算过程的中间变量
dc：反向传播到输入状态c位置的误差，这个值在每层LSTM循环完全结束后会被抛弃，本质是计算过程的中间变量
dWx：输入x对应的权重矩阵Wx，每个时间步计算结果累加
dWh：输入h对应的权重矩阵Wh，每个时间步计算结果累加
db：偏置项对应的权重矩阵b，每个时间步计算结果累加

程序中定义了很多零矩阵，只有dprev_c，dprev_h作为入参进行计算，其他都是负责接收输出的值。

#############################################################################
# TODO: 两个for循环实现：N层堆叠LSTM模型，每个sample包含T个时间步，的backward计算
# Inputs:
# - dh: 全连接层反向传入堆叠LSTM中的，最后一个LSTM层的，误差矩阵(N, T, H)
# - cache: 前向传播过程中产生的中间变量，如f,i,g,o,H,C等
# Returns a tuple of:
# - dx: 存储 包含T个时间步的误差矩阵(N, T, D)
# - dWx: 存储 输入x<-控制门 权重矩阵的梯度(D, 4H)
# - dWh: 存储 状态h<-控制门 权重矩阵的梯度(H, 4H)
# - db: 偏置项的梯度(4H,)
#############################################################################
def lstm_backward(self, dh):
    dx, dh0, dWx, dWh, db = None, None, None, None, None
    #(32, 1, 30)
    N, T, H = dh.shape
    # 获取第一层输入的shape，第一层输入矩阵和隐藏层前向传播矩阵shape不同，lstmParams包含Wx Wh b h c cache
    x, _, _, _, _, _, _, _, _, _ = self.lstmParams[0]['cache'][0]
    #(32, 2)
    D = x.shape[1]
    # dh是全连接层传入的误差矩阵(32, 1, 30)
    dh_prevl = dh
    # 保存各层dwh,dwx,和db
    dweights = []

    for layer in range(self.layersNum - 1, -1, -1):
        # 得到前向传播保存的cache数组
        cache = self.lstmParams[layer]['cache']
        # 如果是第一层网络layer==0，则矩阵shape(DH=D)要与输入矩阵相同；
        # 如果是中间隐藏层矩阵，则shape(DH=H)替换成hidden神经节点数
        DH = D if layer == 0 else H
        # dWx(32, 1, 30)
        dx = np.zeros((N, T, DH))
        # dWx(30, 120)
        dWx = np.zeros((DH, 4 * H))
        # dWh(30, 120)
        dWh = np.zeros((H, 4 * H))
        # db(120,)
        db = np.zeros((4 * H))
        # dprev_h(32, 30)
        dprev_h = np.zeros((N, H))
        # dprev_c(32, 30),上述所有初始化的零矩阵，只有dprev_c，dprev_h是作为参数传入，其他主要作为接收输出用
        dprev_c = np.zeros((N, H))
        # T是一个sample中包含的时间timestep数，对全连接层传入的误差矩阵dh_prevl，按照每个时间步timesteps循环(倒序)，进行反向传播计算
        # 每步计算后将对应的状态存入dx对应的时间步位置，作为下个反向传播层的输入状态dh_prevl，cache是前向传播时记录的中间参数，用于后续求导
        for t in range(T - 1, -1, -1):
            dx[:, t, :], dprev_h, dprev_c, dWx_t, dWh_t, db_t = self.lstm_step_backward(dh_prevl[:, t, :] + dprev_h, dprev_c, cache[t])  # 注意此处的叠加
            dWx += dWx_t
            dWh += dWh_t
            db += db_t

        # 本层求得的n维timestep反向传播误差矩阵dx，作为下一层的输入dh_prevl继续传递；其他dprev_h,dprev_c等变量在当前sample所有时间步计算结束时舍弃。
        # 因为LSTM堆叠时，前向传播除了首层LSTM的输入是训练数据x，后续层的输入都是将上层的输出状态H作为下层的输入x，所以反向传播只用回传dx即可
        dh_prevl = dx
        # 存入dweight后续用梯度下降更新矩阵参数
        dweight = (dWx, dWh, db)
        dweights.append(dweight)
    ##############################################################################
    #                               END OF YOUR CODE                             #
    ##############################################################################
    # 返回dx误差和各层参数误差
    return dx, dweights

5.2.步间循环

LSTM反向传播具体的数学推导过程有一定复杂性，参考文章链接如下：

LSTM反向传播原理——LSTM从零实现系列(2)_量化交易领域专家YangZongxian的博客-CSDN博客lstm反向传播原理https://forecast.blog.csdn.net/article/details/128047225?spm=1001.2014.3001.5502

程序里首先定义了变量dnext_c = dnext_c + o*(1-np.tanh(next_c)**2)*dnext_h，其中o*(1-np.tanh(next_c)**2)*dnext_h其实是对应的是下面这个表达式的求导结果：

$H_t=O_t\odot tan(C_t)$

求导结果如下：

$\frac{\partial E}{\partial C_{t}}+\frac{\partial E}{\partial H_{t}}\cdot O_t\left [ 1-tan^{2}(C_t) \right ]$

di，df，do，dg分别对应四个控制门的求导结果，在最后合并成dz时根据每个控制门使用的激活函数不同，乘以对应的求导结果，如：o*(1 - o) 对应的是sigma导数，(1-g^2) 对应的是tanh导数。

对于 $dx$ ， $dW_x$ ， $dW_h$ 等，出现左乘转置和右乘转置的表达式，也是LSTM不同路径中误差反向传播对应的一部分，其转置原理类似矩阵的逆计算：

$\left\{\begin{matrix} x*w=z \\ x=z*w^T \\ w=x^T*z \end{matrix}\right.$

#############################################################################
# TODO: 每一个Timestep中的LSTM反向传播具体算法实现 
# Inputs:
# - dnext_h: 反向传播参数H_t(N, H)
# - dnext_c: 反向传播参数C_t(N, H)
# - cache: 前向传播过程中产生的中间参数
# Returns a tuple of:
# - dx: 反向传播到x的误差(N, D)
# - dprev_h: 反向传播到H_{t-1}的误差(N, H)
# - dprev_c: 反向传播到C_{t-1}的误差(N, H)
# - dWx: 输入x->控制门的梯度矩阵(D, 4H)
# - dWh: 状态h->控制门的梯度矩阵(H, 4H)
# - db: 偏置项梯度(4H,)
#############################################################################
def lstm_step_backward(self, dnext_h, dnext_c, cache):
    """
    LSTM计算技巧说明 ：
    i_t = σ(W_xi*x_t + W_hi*h_(t-1) + b_i)
    f_t = σ(W_xf*x_t + W_hf*h_(t-1) + b_f)
    o_t = σ(W_xo*x_t + W_ho*h_(t-1) + b_o)
    c^_t = tanh(W_xc*x_t + W_hc*h_(t-1) + b_c)
    // g_t = tanh(W_ig*x_t + b_ig + W_hg*h_(t-1) + b_hg)
    // c_t = f_t ⊙ c_(t-1) + i_t ⊙ g_t
    c_t = f_t ⊙ c_(t-1) + i_t ⊙ c^_t
    h_t = o_t ⊙ tanh(c_t)
    1.四个参数矩阵di,df,do,dg 都要向前传播,所以合并成一个矩阵dz，在统一和权重矩阵做计算，
      所以我们可以构建一个4倍大小的W，将4个W矩阵拼接起来，计算之后再将4个矩阵分别分离出来，这样可以减少计算量
    2.针对ΔE/ΔC_t_new导数过程示例，除o以外，f i g的反向传播都包含两条求导链，来自C_t和h_t，所以先求出ΔE/ΔC_t_new导数，再代入f i g求导过程
      (1)ht = o_t ⊙ tanh(Ct)
      (2)ΔE/ΔC_t_new = ΔE/ΔC_t + ΔE/(Δh->ΔC)  #根据LSTM模型，可发现ΔE/ΔC_t有两条求导链，都要进行计算，其中一条就是ΔE/ΔC_t
      (3)ΔE/ΔC_t_new = ΔE/ΔC_t + ΔE/Δh*Δh/ΔC_t = ΔE/ΔC_t + ΔE/Δh * (o_t ⊙ tanh(Ct))' = ΔE/ΔC_t + ΔE/Δh * [o_t ⊙ (1-tanh2(C_t))]
    3.针对ΔE/ΔWo_t导数过程示例，先求ΔE/Δo_t，再求ΔE/ΔWo_t <=> [σ(x)]' = σ(x)*(1-σ(x))
      (1)ht = o_t ⊙ tanh(Ct)
      (2)ΔE/Δo_t = ΔE/Δh * Δh/Δo_t = ΔE/Δh * Δ[o_t ⊙ tanh(Ct)]/Δo_t = ΔE/Δh * tanh(Ct)
      (3)o_t = σ(W_xo*x_t + W_ho*h_(t-1) + b_o)
      (4)σ' = σ(1-σ)
      (5)ΔE/ΔWo_t = ΔE/Δh * Δh/Δo_t * Δo_t/ΔWo_t = ΔE/Δo_t * Δo_t/ΔWo_t = ΔE/Δo_t * (o_t)' = ΔE/Δo_t * [σ(W...)]' = (ΔE/Δo_t) * {σ(W+...) * [1-σ(W+...)]} = (ΔE/Δo_t) * o_t * (1-o_t)
      (6)ΔE/ΔWo_t = (ΔE/Δo_t) * o_t * (1-o_t) = ΔE/Δh * tanh(Ct) * o_t * (1-o_t)
    4.针对ΔE/ΔWc^_t(即ΔE/ΔWg_t)导数过程示例，先求ΔE/Δc^_t(即ΔE/Δg_t)，再求ΔE/ΔWc^_t = ΔE/ΔWg_t <=> [tanh(x)]' = 1-tanh2(x)
      (1)c_t = f_t ⊙ c_(t-1) + i_t ⊙ c^_t
      (2)ΔE/Δg_t = ΔE/Δc_t * Δc_t/Δg_t = ΔE/Δc_t * Δ[f_t ⊙ c_(t-1) + i_t ⊙ g_t]/Δg_t = ΔE/Δc_t * i_t
      (3)g_t = tanh(W_ig*x_t + b_ig + W_hg*h_(t-1) + b_hg)
      (4)tanh'(x) = 1-tanh2(x)
      (5)ΔE/ΔWg_t = ΔE/Δc_t * Δc_t/Δg_t * Δg_t/ΔWg_t = ΔE/Δg_t * Δg_t/ΔWg_t = ΔE/Δg_t * (g_t)' = ΔE/Δg_t * [tanh(W...)]' = (ΔE/Δc_t * i_t) * (1-tanh2(W...)) = (ΔE/Δc_t * i_t) * (1 - g_t^2)
    5.在求出上述三个导数ΔE/ΔC_t_new ~ dnext_c、ΔE/ΔWo_t ~ do、ΔE/ΔWc^_t ~ dg后，代入后续表达式即可
    """
    dx, dprev_h, dprev_c, dWx, dWh, db = None, None, None, None, None, None
    #x(32, 30)prev_h(32, 30)(32, 30)(30, 120)(30, 120)i(32, 30)(32, 30)(32, 30)(32, 30)(32, 30)
    x, prev_h, prev_c, Wx, Wh, i, f, o, g, next_c = cache

    # ΔE/ΔC_t_new = ΔE/ΔC_t + (Δh->ΔC)，每个LSTM单元反向传播起始点包含C_t和H_t两条路径，所以此处进行了一个求和操作
    # next_h=o*np.tanh(next_c)，将求出的Δh/ΔC_t代入上式可得 => ΔE/(Δh->ΔC)=ΔE/Δh*Δh/ΔC_t = o*(1-np.tanh(next_c)**2)*ΔE/Δh
    dnext_c = dnext_c + o * (1 - np.tanh(next_c) ** 2) * dnext_h  
    # next_c = f*prev_c + i*g
    di = dnext_c * g
    df = dnext_c * prev_c
    # next_h = o*np.tanh(next_c)
    do = dnext_h * np.tanh(next_c)
    dg = dnext_c * i
    # next_c = f*prev_c + i*g
    dprev_c = f * dnext_c
    # 水平合并figo四部分(32, 120)
    dz = np.hstack((i * (1 - i) * di, f * (1 - f) * df, o * (1 - o) * do, (1 - g ** 2) * dg))  

    # 1.(32, 120)*(30,120).T = (32, 30) 
    # 2.(32, 120)*(30,120).T = (32, 30) 
    # 3.(32, 120)*(2,120).T=(32,2)
    dx = Tools.matmul(dz, Wx.T)
    # 1.(32, 120)*(30,120).T = (32, 30)
    # 2.(32, 120)*(30,120).T = (32, 30)
    # 3.(32, 120)*(30,120).T = (32, 30) 
    dprev_h = Tools.matmul(dz, Wh.T)
    # 1.(32, 30).T * (32, 120)=(30, 120)
    # 2.(32, 30).T * (32, 120)=(30, 120)
    # 3.(32,2).T * (32, 120)=(2,120)
    dWx = Tools.matmul(x.T, dz)
    # 1.(32, 30).T * (32, 120)=(30, 120)
    # 2.(32, 30).T * (32, 120)=(30, 120)
    # 3.(32, 30).T * (32, 120)=(30, 120)
    dWh = Tools.matmul(prev_h.T, dz)
    # 1,2,3:(32, 120)=>(120,)
    db = np.sum(dz, axis=0)

    ##############################################################################
    #                               END OF YOUR CODE                             #
    ##############################################################################
    return dx, dprev_h, dprev_c, dWx, dWh, db

3层LSTM全部循环计算完成后，最后一层的输出参数如下所示，这里要注意首层对应的 $dW_x$ 和其它层层对应的 $dW_x$ 的shape不一样：

dx.shape(32,1,2)

dWx.shape(2,120)

dWh.shape(30,120)

db.shape(123,)

5.3.权重矩阵参数的更新

误差矩阵计算完成后，还要对全连接层的权重矩阵和偏置项进行更新，这里使用的更新函数是getUpdWeights((Wx,Wh,b),(dWx,dWh,db), lrt)。

首先将当前的权重矩阵(Wx,Wh,b)和误差矩阵(dWx,dWh,db)传入getUpdWeights，配合着学习率lr，使用Adam优化器进行梯度更新，也就是更新LSTM层中的三个权重矩阵Wx.shape(, )，Wh.shape(, )和偏置项b.shape(,)的参数。

我们也正是通过误差矩阵在每一层进行反向传播计算过程中得到的 $dW_x$ ， $dW_h$ ， $db$ ，结合Adma等算法，来更新每一层权重矩阵 $W_x$ ， $W_h$ ， $b$ 的参数。其中Adma等算法也只是通过调整权重参数的更新方式，从而提升了损失函数的收敛速度。

# 计算反向传播权重梯度w,b
def bpWeights(self, input, lrt):
    # dw = Tools.matmul(input.T, self.deltaOri)
    # inputReshaped是正向传播时上层网络传到本层的输入矩阵，deltaOri是本层反向传播激活函数求导后的误差矩阵
    dw = Tools.matmul(self.inputReshaped.T, self.deltaOri)
    # 误差矩阵deltaOri.shape->(32,10),进行sum计算后将32个sample向量对应位置求和后db.shape->(1,10)，再reshape成b.shape用于后续梯度优化
    db = np.sum(self.deltaOri, axis=0, keepdims=True).reshape(self.b.shape)
    # 当前层网络权重(w,b)元组
    weight = (self.w,self.b)
    # 反向传播的权重(dw,db)元组
    dweight = (dw,db)
    # 元组按引用对象传递，值在方法内部已被更新
    # 将两个元组代入优化器，求出梯度方向，根据梯度更新参数，更新了self.lstmParams[i][Wx,Wh,b]的权重矩阵
    self.optimizerObj.getUpdWeights(weight,dweight, lrt)

到这里，一个完整的反向传播过程就完成了：这个过程通过将损失函数计算出的损失值不断向前传递，传递的过中模型不断的更新其每一层包含的权重矩阵中的参数；通过不断修改权重矩阵的参数使得后续预测产生的损失值越来越小，从而使得模型预测的结果越来越准确。

权重参数更新也是反向传播的意义和最终目的。