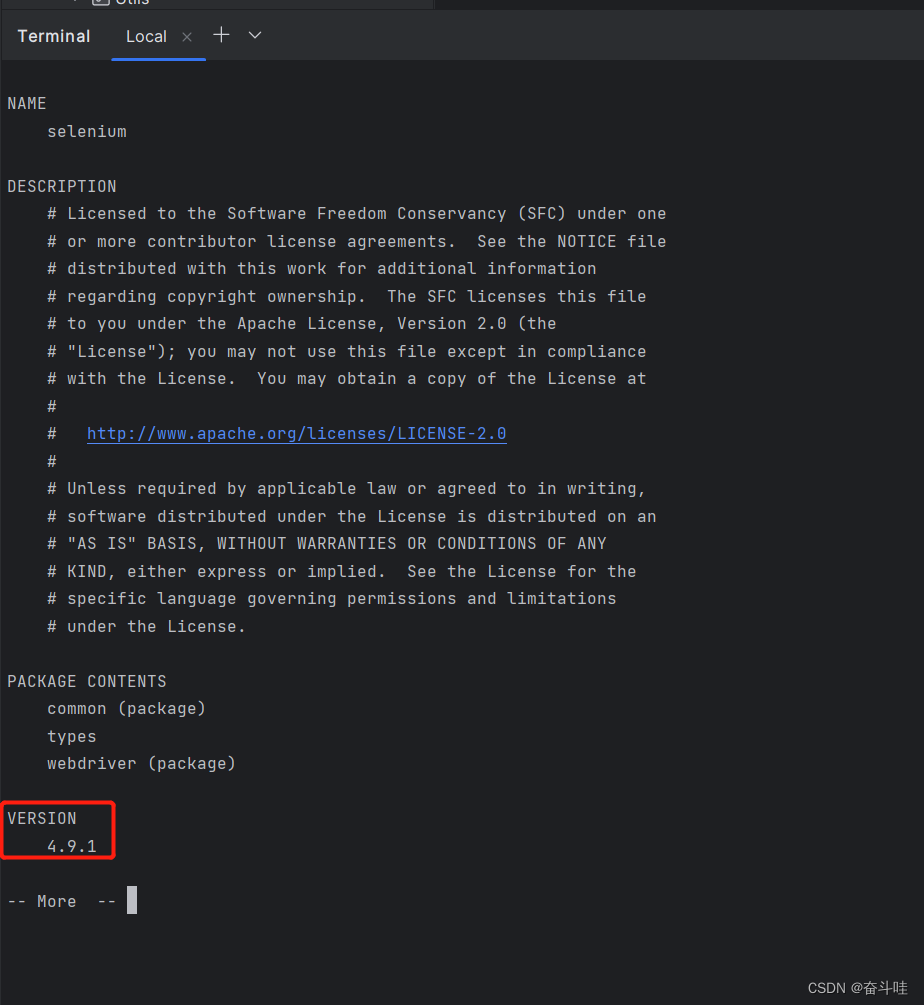
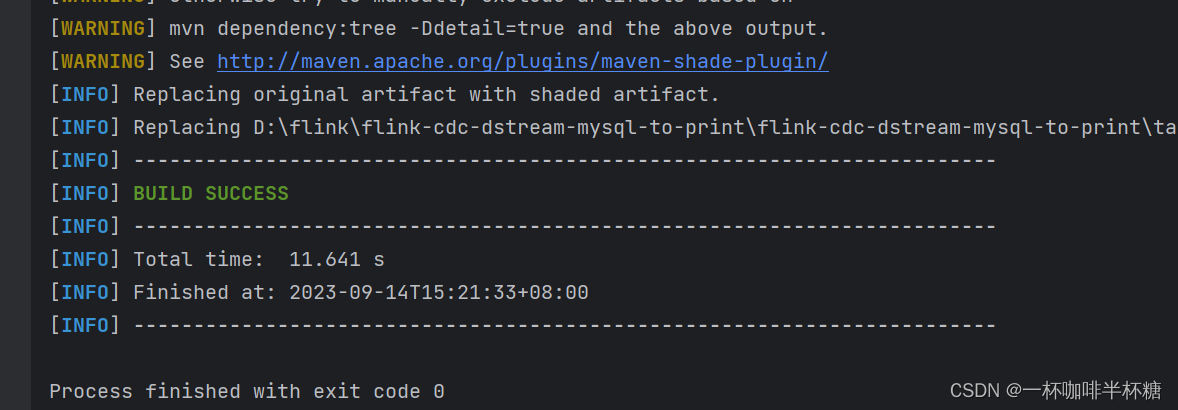
广义表 (又称列表 Lists)是 n >= 0个元素 . a0,a1....an-1的有限序列，其中每一个 ai 或者是原子，或者是一个广义表

广义表通常记作: LS = (a1，a2，.....，an）， LS为表名，n为表的长度，每一个 ai 为表的元素，一般用大写字母表示广义表，小写字母表示原子

表头: 若 LS非空(n>=1)，则其第一个元素 就是表头，表头可以是原子，也可以是子表记作 , head(LS)= a1

表尾：除表头之外的其它元奏组成的表 记作 tail(LS =(a2...., an)。表尾不是最后一个元素，而是一个子表

【案例】

广义表的性质

（1）广义表中的数据元素有相对次序，一个直接前驱和一个直接后继

（2）广义表的长度定义为最外层所包含元素的个数。如:C=(a (b)) 是长度为2的广义表

（3）广义表的深度定义为该广义表展开后所含括号的重数 A=(b，c) 的深度为1，B=(A,d) 的深度为 2，C=(f，B，h）的深度为3

注意:“原子”的深度为 0;“空表”的深度为 1。

（4）广义表可以为其他广义表共享; 如: 广义表 B就共享表A。在B中不必列出A的值，而是通过名称来引用，B= (A)

（5） 广义表可以是一个递归的表。如: F(a，F）= (a(a,(a ...)))

注意: 递归表的深度是无穷值，长度是有限值。

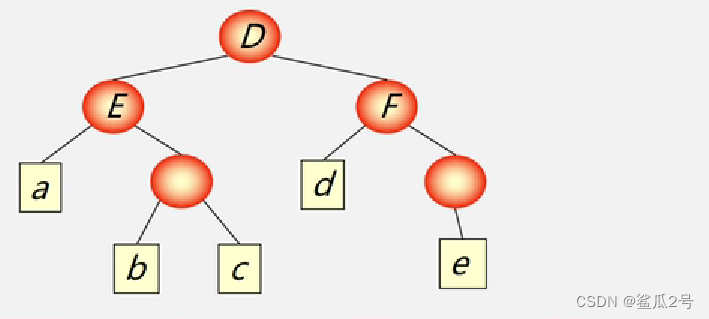
（6）广义表是多层次结构，广义表的元素可以是单元素，也可以是子表，而子表的元素还可以是子表，可以用图形象地表示

例: D=(E，F)，其中: E=(a(b,c))，F=(d(e))

广义表和线性表的区别？

广义表可以看成是线性表的推广，线性表是广义表的特例。

广义表的结构相当良活，在某种前提下，它可以兼容线性表、数组树和有向图等各种常用的数据结构。

当二维数组的每行(或每列) 作为子表处理时，二维数组即为一个广义表。

另外，树和有向图也可以用广义表来表示

由于广义表不仅集中了线性表、数组、树和有向图等常见数据结构的特点

而且可有效地利用存储空间，因此在计算机的许多应用领域都有成功使用广义表的实例。