中心频率 $f_c\mathrm{Hz}$
3dB陷波器带宽 $f_b\mathrm{Hz}$
陷波器深度 $d$ 倍，即 $20\log (d)\mathrm{dB}$

则
$$\begin{array}{rl}B& =2\pi f_b\\ {\omega }_n& =2\pi f_c\end{array}$$

定义

$$\begin{array}{rl}{\xi }_1& =\sqrt{\frac{1-\sqrt{1+\frac{B^2}{{\omega }_n^2}}}{4d^2-2}}\\ {\xi }_2& =d{\xi }_1\end{array}$$

则传递函数为
$$G(s)=\frac{s^2+2{\xi }_2{\omega }_{n}s+{\omega }_n^2}{s^2+2{\xi }_1{\omega }_{n}s+{\omega }_n^2}$$

fwb = 10; % 3dB截至频率 Hz
fc = 100; % 中心频率 Hz

B = 2*pi*fwb;
Wn = 2*pi*fc;
depth = 0.1;

k1 = sqrt((1-sqrt(1+B^2/Wn^2)) / (4*depth^2-2));
k2 = depth * k1;


num = [1, 2*k2*Wn, Wn^2];
den = [1, 2*k1*Wn, Wn^2];

G = tf(num,den);

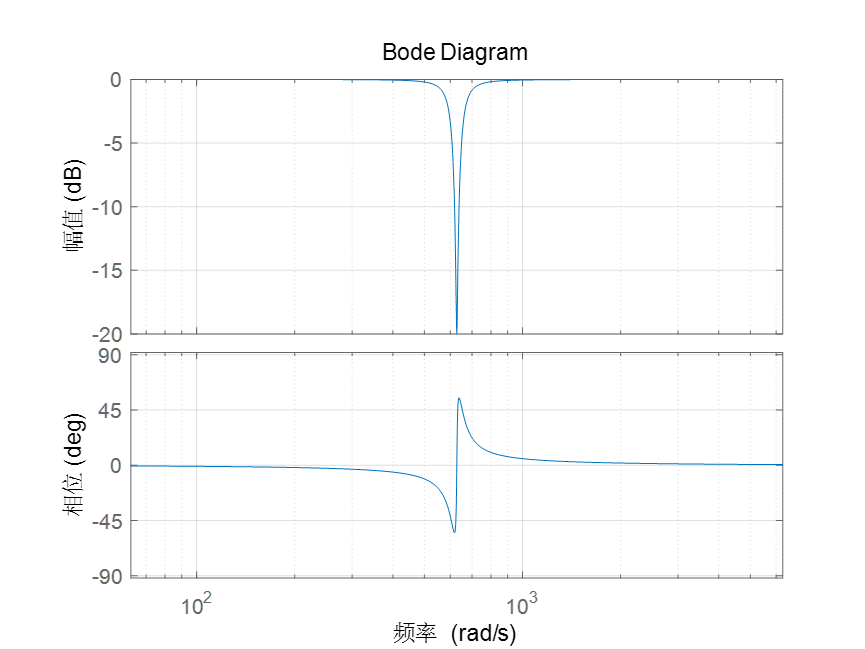
figure(1)
bode(G, 10*2*pi:0.01:1000*2*pi);
grid on;

figure(2);
[mag,phase,wout] = bode(G, 10*2*pi:0.01:1000*2*pi);
semilogx(wout/(2*pi), 20*log10(squeeze(mag)));
grid on;
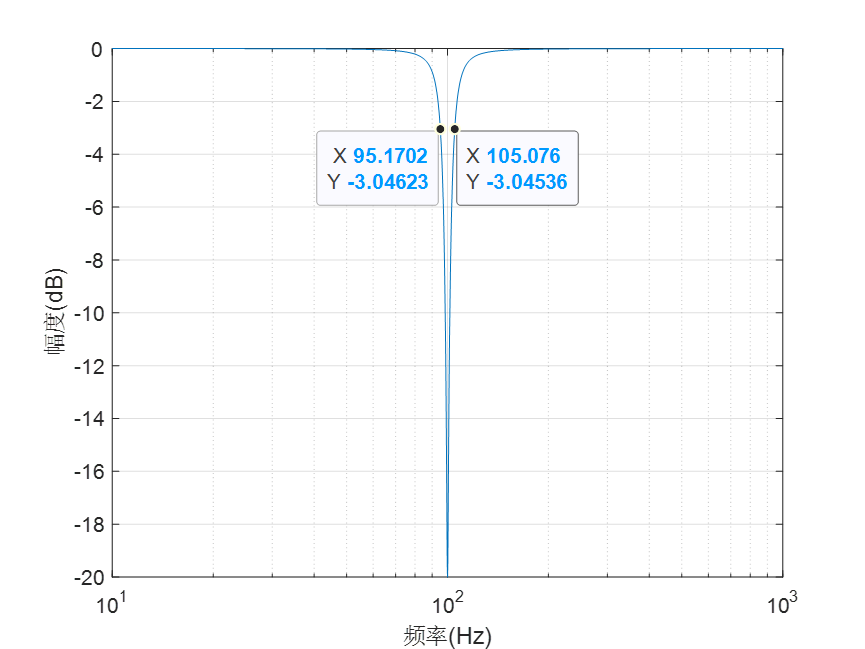
xlabel('频率(Hz)')
ylabel('幅度(dB)')

——完——