文章目录
- 参考文章及视频
- 导言
- 梯度下降的原理、过程
- 一、什么是梯度下降?
- 二、梯度下降的运行过程
- 批量梯度下降法(BGD)
- 随机梯度下降法(SGD)
- 小批量梯度下降法(MBGD)
- 梯度算法的改进
- 梯度下降算法存在的问题
- 动量法(Momentum)
- 目标
- 改进思想
- 为什么有效
- 动量法还有什么效果?
- 自适应梯度(AdaGrad)
- AdaGrad存在的问题
- AdaGrad算法具有以下特点:
- RMSProp
- ADAM梯度下降法
- 总结
参考文章及视频
耿直哥讲AI:https://www.bilibili.com/video/BV18P4y1j7uH/?spm_id_from=333.337.search-card.all.click&vd_source=f6c19848d8193916be907d5b2e35bce8
计算机视觉与深度学习 北京邮电大学 鲁鹏 清晰版合集(完整版):https://www.bilibili.com/video/BV1V54y1B7K3?p=5&vd_source=f6c19848d8193916be907d5b2e35bce8
导言
梯度下降的原理、过程
一、什么是梯度下降?
梯度下降(Gradient Descent)是一种常用的优化算法,主要用于寻找函数的局部最小值。在机器学习和深度学习中,我们通常使用梯度下降来优化损失函数,从而找到使损失最小的模型参数。
梯度在数学上可以看作是函数在某一点的斜率,或者说是函数在该点变化最快的方向。在多维空间中,梯度是一个向量,指向函数增长最快的方向。而"梯度下降"的思想就是,如果我们想找到函数的最小值,那么从当前位置沿着梯度的负方向,即函数下降最快的方向,进行迭代更新就可能找到这个最小值。
通俗的来讲就是:
- 想象一下你置身于一个大山谷中,你的目标是找到山谷最低处的位置。但是你没有地图,也不能一下子看到整个山谷的形状。所以你只能根据自己当前所处位置的周围情况来判断往哪个方向走。
- 梯度下降法就像是你通过观察地势斜率来下山。你站在某个位置上,然后观察周围的地势斜率。地势斜率的方向指示了最陡下坡的方向,而你的目标是下到山谷的最低点。
- 开始时,你随机选择一个位置作为起点。然后你观察当前位置的地势斜率,并朝着斜率最陡的方向迈出一步。然后,你再次观察新位置的地势斜率,并再次朝着最陡的方向迈出一步。你不断重复这个过程,每次都往下坡最陡的方向前进,直到你无法再下降或者到达了山谷的最低点。
- 通过这种迭代的方式,你能够一步步地接近山谷的最低点,也就是最优解。梯度下降法通过不断地调整位置,最终找到了函数的最小值点(或者最大值点)。
如图所示:

陡峭度=梯度
需要注意的是,梯度下降法中的步长(学习率)很重要。
如果步长太大,你可能会错过最低点;
如果步长太小,你会花费很长的时间才能到达最低点。
所以选择一个合适的步长是梯度下降法的一个关键因素。
二、梯度下降的运行过程
梯度下降的过程很直观,可以分为以下几个步骤:
- 初始化参数:给定一个初始点。
- 计算梯度:在当前点,计算函数的梯度,即各个参数的偏导数。
- 更新参数:按照以下公式更新参数:θ = θ - α * ∇f(θ)。其中,θ代表当前的参数,α是学习率(决定了步长的大小),∇f(θ)是函数在θ处的梯度。
- 迭代更新:重复步骤2和步骤3,直到梯度接近0,或者达到预设的迭代次数。
这个过程会持续进行,直到找到一个足够好的解,或者达到预设的迭代次
批量梯度下降法(BGD)
批量梯度下降(Batch Gradient Descent)是梯度下降算法的一种变体,用于优化机器学习模型的参数。与其他梯度下降算法相比,批量梯度下降在每次迭代中使用整个训练数据集来计算梯度和更新参数。
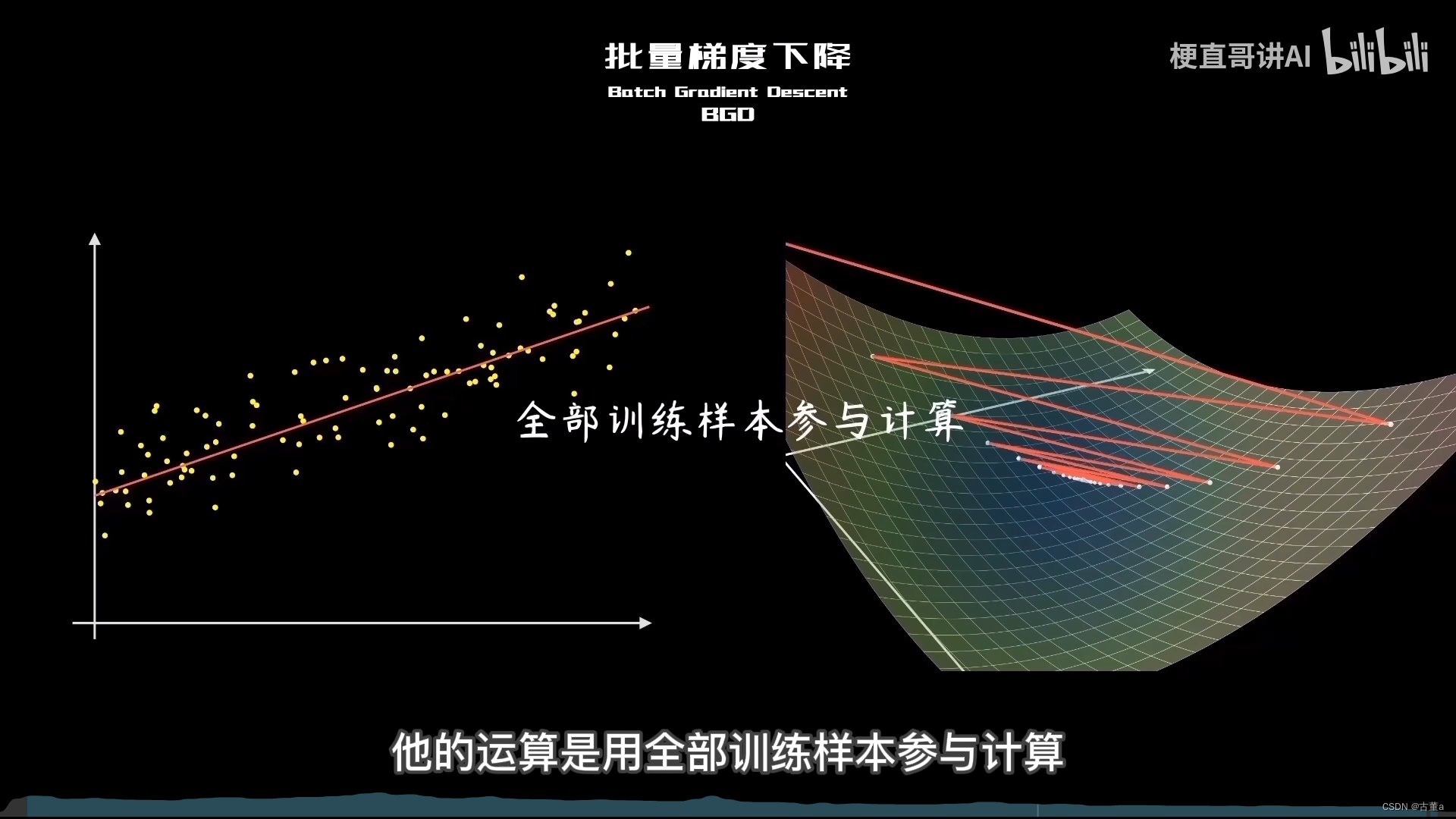
批量梯度下降通常用于小型数据集或参数空间较小的模型。
- 它的优点是能够更准确地收敛到全局最优解(如果存在),并且在参数更新方向上相对稳定。
- 然而,由于每次迭代时都要使用整个数据集,因此它的计算成本较高。尤其是在大规模数据集上。
随机梯度下降法(SGD)
随机梯度下降(Stochastic Gradient Descent,SGD)是一种梯度下降算法的变体,用于优化机器学习模型的参数。与批量梯度下降不同,随机梯度下降在每次迭代中仅使用一个样本来计算梯度和更新参数。
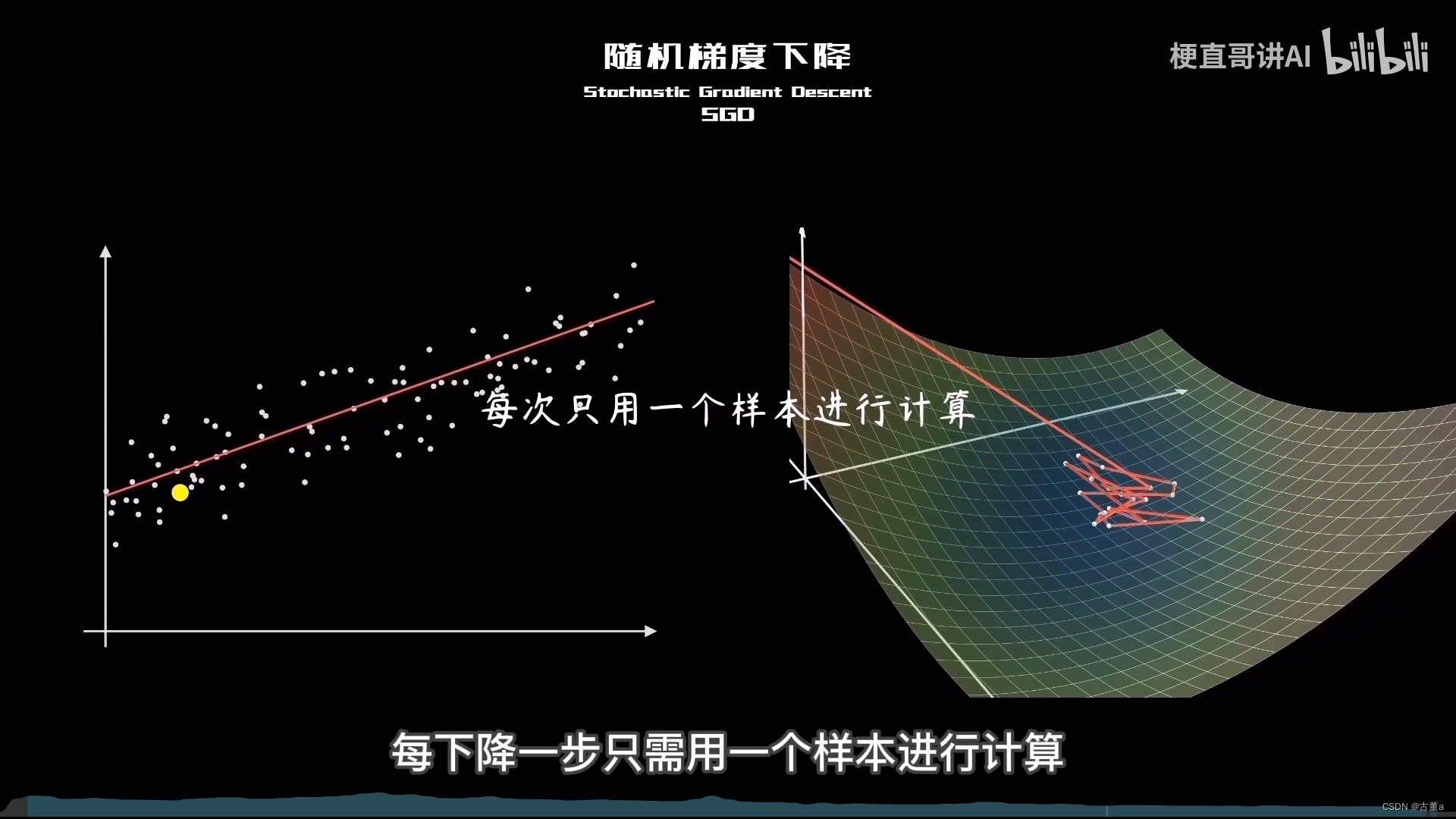
随机梯度下降是一种每次迭代仅使用一个样本来计算梯度并更新参数的梯度下降算法。
- 它的优点是计算代价较低,适用于大规模数据集,这一特性有助于算法逃离局部最小值,并具有一定的探索性。
- 然而,由于梯度估计存在噪音,参数更新可能不稳定。
小批量梯度下降法(MBGD)
小批量梯度下降(Mini-Batch Gradient Descent)是梯度下降算法的一种变体,介于批量梯度下降(Batch Gradient Descent)和随机梯度下降(Stochastic Gradient Descent)之间。
它在每次迭代中使用一小批次(mini-batch)的样本来计算梯度和更新参数。
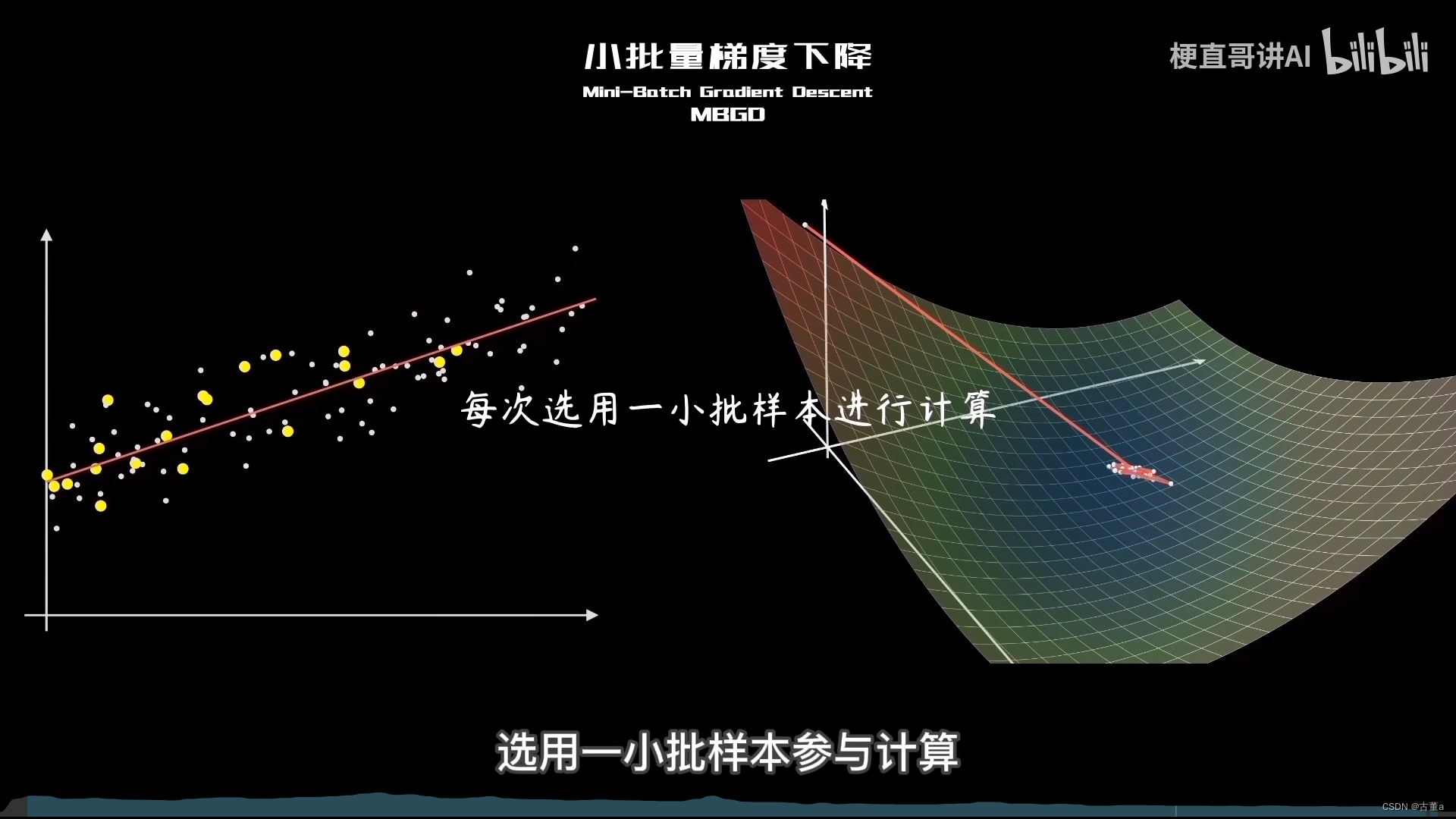
梯度算法的改进
梯度下降算法存在的问题
损失函数特性:一个方向上变化迅速而在另一个方向上变化缓慢。
优化目标:从起点处走到底端笑脸处。
梯度下降算法存在的问题:山壁间振荡,往谷底方向的行进较慢。
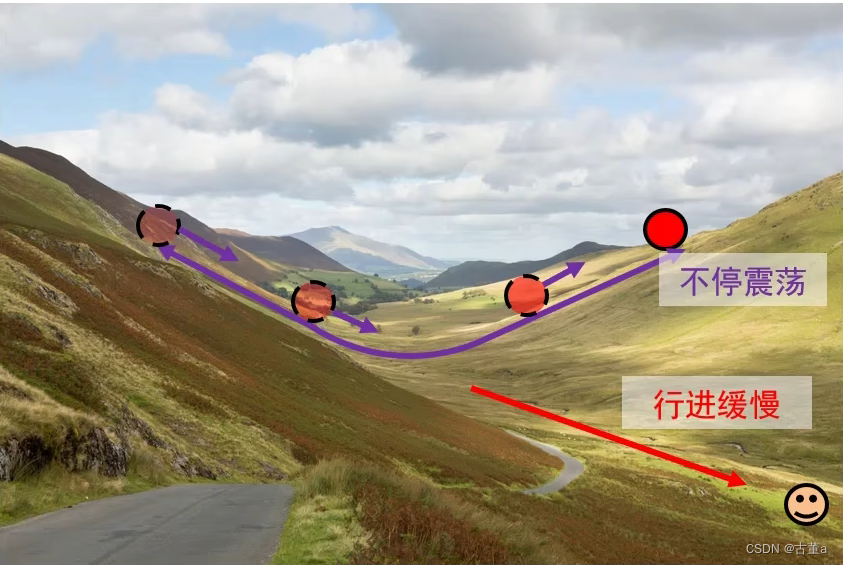
仅增大步长并不能加快算法收敛速度:相当于在振荡方向加了一个更大的速度,往山谷方向也加了,但是很小。
动量法(Momentum)
动量法梯度(Momentum Gradient Descent)下降通过引入动量变量,可以在更新过程中积累之前的梯度信息,并根据历史梯度的趋势来调整参数更新的方向和幅度。这样可以使参数更新在梯度方向上更加稳定,并且可以加速学习过程,尤其在目标函数存在大体量或弯曲的情况下。
目标
改进梯度下降算法存在的问题,即减少震荡,加速通往谷底
改进思想
利用累加历史梯度信息更新梯度

μ取值范围[0,1)
- 当动量系数μ等于0时,动量法梯度下降变为普通的梯度下降算法。在这种情况下,动量变量v的更新公式简化为:
v = 0 * v + g = g
也就是说,动量变量v只受当前梯度的影响,而不考虑历史梯度信息。参数更新时,只使用当前梯度乘以学习率进行更新。这样的更新方式使得参数更新的方向和幅度完全依赖于当前的梯度值。 - 当动量系数μ等于1时,动量法梯度下降完全依赖于历史梯度信息。动量变量v的更新公式为:
v = 1 * v + g = v + g
动量变量v实际上就是历史梯度的累积,因为历史梯度乘以1之后仍然是历史梯度本身。在参数更新时,只使用动量变量v进行更新,而不再考虑当前梯度的贡献。 即使g走到平坦局域了为0 了,可是v不为0,则权值θ还在持续更新。
建议取0.9,可以将其理解为摩擦系数 v = 0.9v 多次迭代后,v会接近于0
为什么有效
累加过程中震荡方向相互抵消,平坦方向得到加强
动量法还有什么效果?
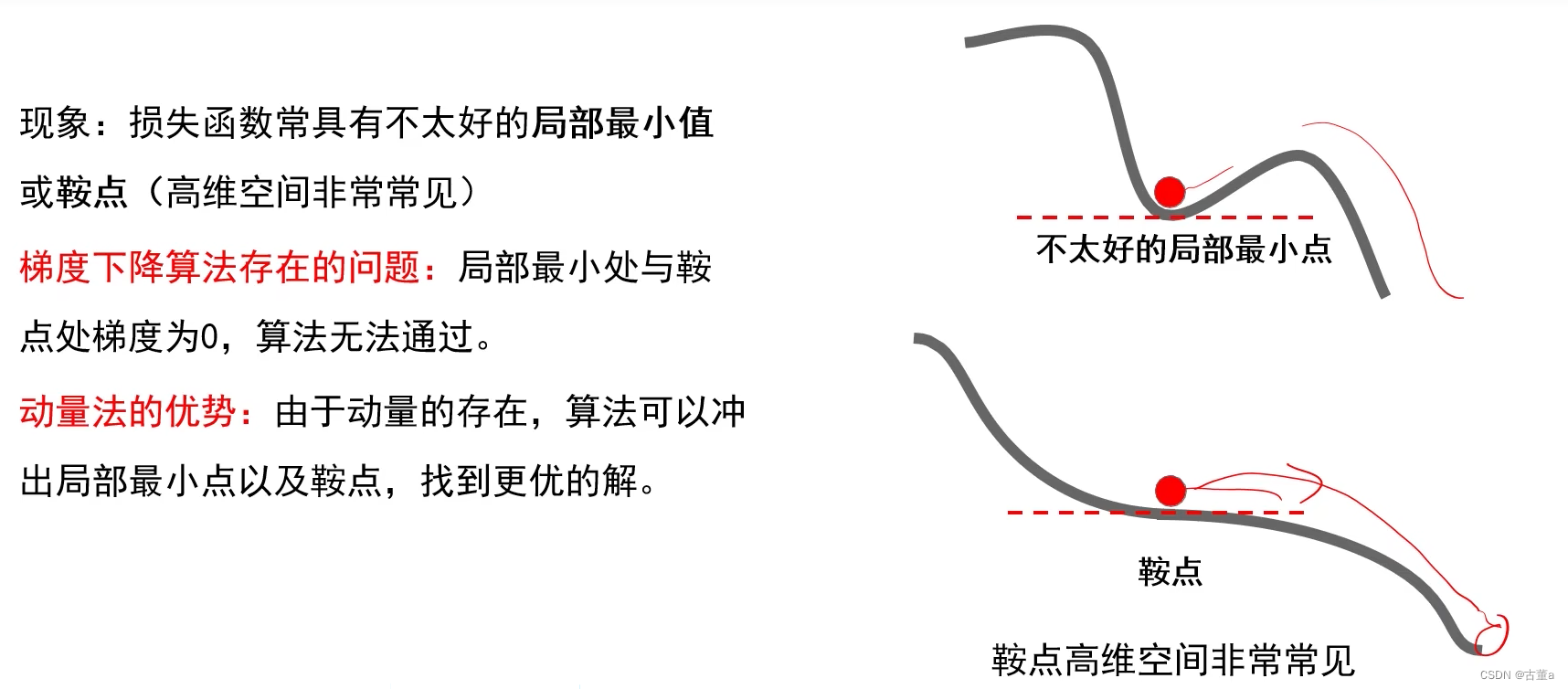
它在参数更新中引入了动量概念,以加速学习过程并帮助跳出局部最优解和鞍点。
自适应梯度(AdaGrad)
AdaGrad(Adaptive Gradient Algorithm)是一种自适应梯度算法,用于在机器学习中优化模型的参数。它根据参数的梯度历史信息自适应地调整学习率,使得在训练过程中较大的梯度得到较小的学习率,而较小的梯度得到较大的学习率。
AdaGrad算法的核心思想是为每个参数维护一个梯度的累积平方和,并在参数更新时将学习率除以这个累积平方和的平方根。

如何区分震荡方式与平坦方向?
梯度幅度的平方较大的方向是震荡方向;
梯度幅度的平方较小的方向是平坦方向。

震荡方向和平坦方向的梯度的平方和不断累加
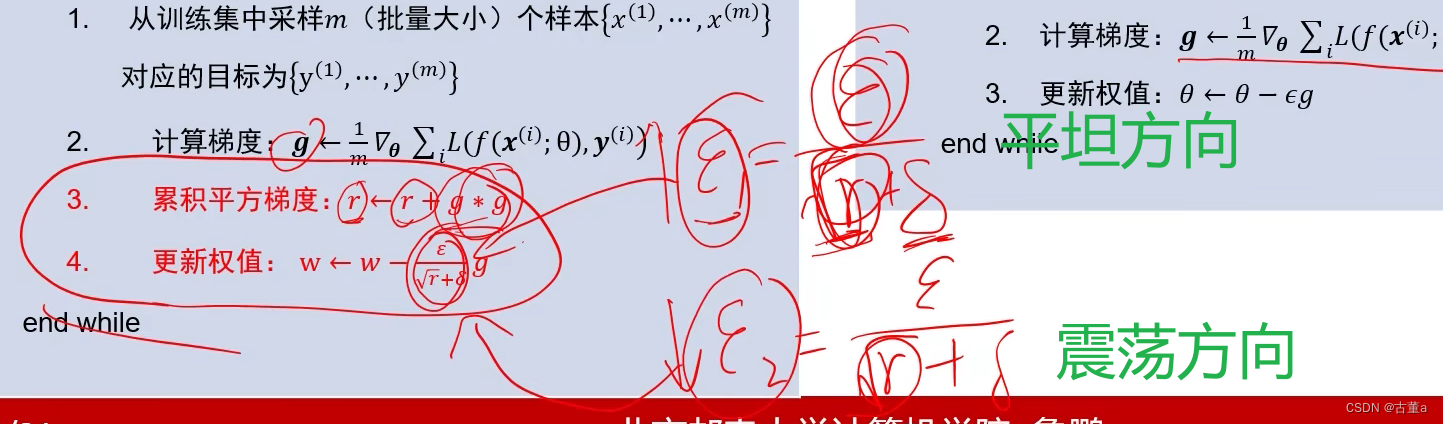
因为震荡方向的梯度大,因此累加平方梯度r不断变大,所以ε1不断减小
因为平坦方向的梯度小,因此累加平方梯度r不断变肖,所以ε2不断增大
AdaGrad存在的问题
由于累加平方梯度r在不断的变大,在多次迭代后,r会变得非常大,则ε1和ε2都会变成一个非常小的值。失去调节作用。
AdaGrad算法具有以下特点:
-
自适应学习率:AdaGrad算法根据参数的梯度历史信息自适应地调整学习率。当某个参数的梯度较大时,其累积平方和较大,学习率较小;当梯度较小时,累积平方和较小,学习率较大。这样可以保证在训练早期参数更新幅度较大,而在训练后期逐渐减小。
-
处理稀疏梯度:AdaGrad算法在处理稀疏数据集时表现良好。由于累积平方和的累加,较少出现的参数梯度将获得更大的学习率,从而更快地进行参数更新。
-
累积平方和的增长:AdaGrad算法累积了梯度的平方和,随着训练的进行,累积平方和会逐渐增大。这可能导致学习率过度下降,使得训练过程变得缓慢。为了解决这个问题,后续的优化算法如RMSprop和Adam引入了衰减系数,对累积平方和进行平滑衰减。
RMSProp
RMSprop(Root Mean Square Propagation)是一种自适应梯度算法,用于在机器学习中优化模型的参数。它是对AdaGrad算法的改进,主要解决AdaGrad算法累积平方梯度过度增大的问题。
RMSprop算法的核心思想是为每个参数维护一个梯度平方的移动平均,并在参数更新时使用这个移动平均来调整学习率。
算法思路:

当ρ等于0:不考虑历史梯度 ,r = 0 * r + (1 - 0)g * g = g * g 仅依靠当前的的梯度
- 就把梯度大的降低一些,梯度小的增大一些
当ρ等于1:即所有的历史梯度都考虑进来,r = 1 * r + (1 - 1) g * g = r
- 权值一直不会变了
建议取0.999, v = 0.999v + 0.001 * g * g 多次迭代后,v会不断减小
ADAM梯度下降法
Adam(Adaptive Moment Estimation)是一种自适应梯度算法,结合了动量法和RMSprop算法的优点,用于在机器学习中优化模型的参数。它在训练过程中自适应地调整学习率
算法思路:

修正偏差为什么可以缓解冷启动?
在进行第1次更新的时候:
v初始值为0,μ初始值为0.9
v
(
1
)
=
0
+
0.1
g
v^{(1)} = 0 + 0.1 g
v(1)=0+0.1g
则通过修正偏差
v
^
1
=
0.1
g
/
1
−
(
0.9
)
1
=
g
\hat{v}^1 = 0.1 g / 1 - (0.9)^1= g
v^1=0.1g/1−(0.9)1=g
解决了开始的梯度被减少10倍的问题
在进行第10次更新的时候:
修正偏差项就不起作用了
v
^
10
=
v
9
g
/
1
−
(
0.9
)
10
=
v
\hat{v}^{10} = v^9 g / 1 - (0.9)^{10} = v
v^10=v9g/1−(0.9)10=v
所以修正项仅在初期为了解决冷启动的时候起作用,来防止初期r = v = 0,更新特别慢的问题
总结
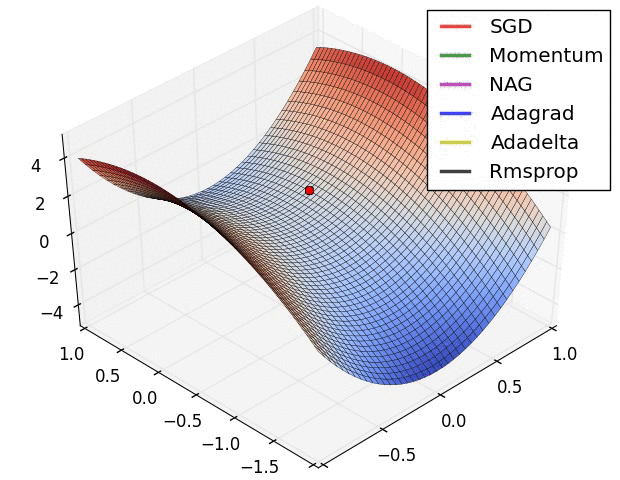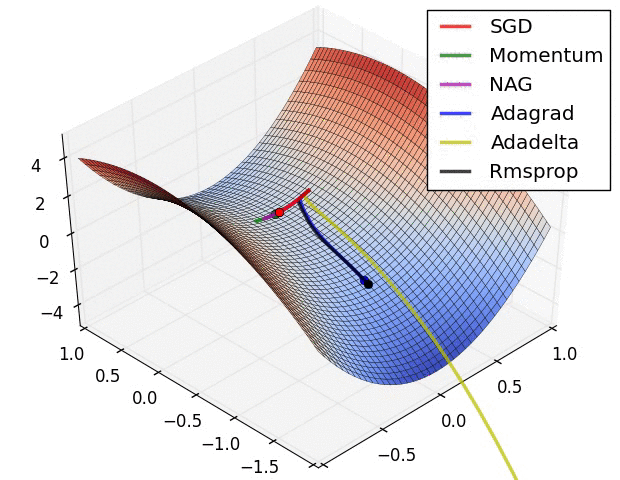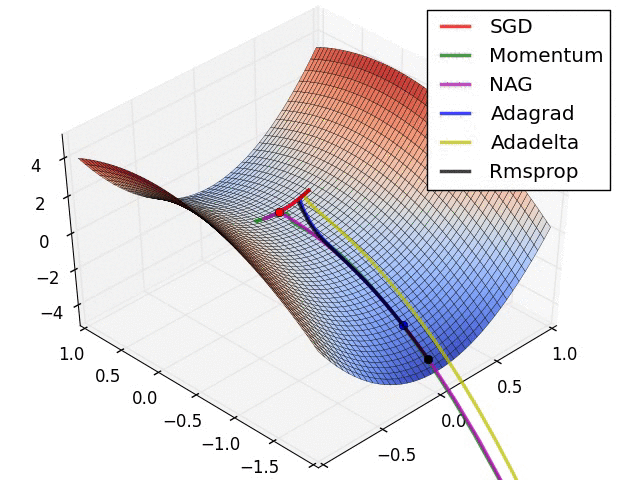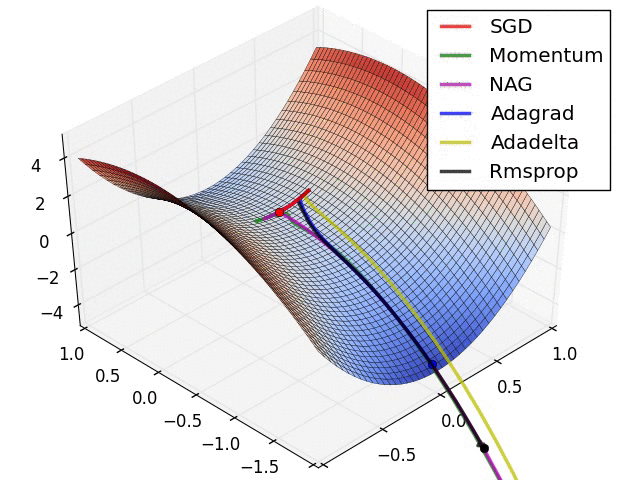
分享一个动态查看各种梯度梯度算法下降过程的图的网站https://www.ruder.io/optimizing-gradient-descent/
这个博主写的更多更详细:https://blog.csdn.net/oppo62258801/article/details/103175179?ydreferer=aHR0cHM6Ly93d3cuYmluZy5jb20v

同时可以学习一下算法的实现:https://zhuanlan.zhihu.com/p/77380412