NuGet安装MathNet.Numerics
引用:
using MathNet.Numerics.Random;
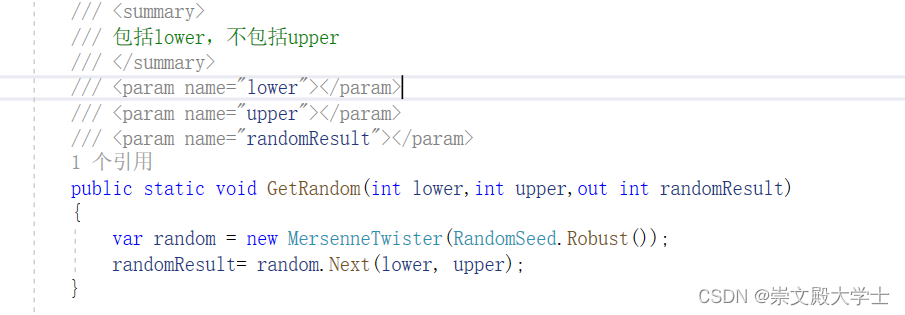
/// <summary>
/// 包括lower,不包括upper
/// </summary>
/// <param name="lower"></param>
/// <param name="upper"></param>
/// <param name="randomResult"></param>
public static void GetRandom(int lower,int upper,out int randomResult)
{
var random = new MersenneTwister(RandomSeed.Robust());
randomResult= random.Next(lower, upper);
}
Mersenne Twister算法是一种伪随机数发生器,名字来源于其周期长度通常取自Mersenne质数。它是由Makoto Matsumoto(松本)和Takuji Nishimura(西村)于1997年开发的,基于有限二进制字段上的矩阵线性再生。它的主要作用是生成伪随机数,并修正了古老随机数生成算法的许多缺陷。
Mersenne Twister算法利用线性反馈移位寄存器(LFSR)生成随机数。这个寄存器的反馈函数是某些位的简单异或,这些位也被称为抽头序列。一个n位的LFSR能在重复之前产生2n-1位长的伪随机序列。只有具有特定抽头序列的LFSR才能通过所有2n-1个内部状态,产生2^n-1位长的伪随机序列,这个输出序列就称为m序列。为了使LFSR成为最大周期的LFSR,由抽头序列加上常数1形成的多项式必须是本原多项式。
Mersenne Twister算法具有一些显著的优点。它生成的随机数质量好,随机性高,可以在计算机上容易实现,占用内存较少。与其他已使用的伪随机数发生器相比,它的运行速度更快,周期更长,可以达到2^19937-1,并且具有623维均匀分布的性质。对于一般的应用来说,这个周期长度已经足够了。此外,它的序列关联较小,能通过很多随机性测试。在计算机科学和工程领域,Mersenne Twister算法被广泛用于需要产生随机数的情况。