目录

一、仿函数 

二、priority_queue(优先级队列)

1、概念：

2、使用：

3、数组中第K个最大元素

4、priority_queue的模拟实现

---

一、仿函数 

①、概念：

仿函数，即函数对象。一种行为类似函数的对象，调用者可以像函数一样使用该对象，其实现起来也比较简单：用户只需实现一种新类型，在类中重载operator()即可，参数根据用户所要进行的操作选择匹配。

②、代码：

•  用内置类型比较大小关系：

//仿函数/函数对象 --- 对象可以像调用函数一样去使用
struct less
{
	//()运算符重载--用于比较大小
	bool operator()(int x, int y)
	{
		return x < y;
	}
};

• 利用模板比较less： 

template<class T>
struct less//用于 < 的比较
{
	bool operator()(const T& x, const T& y) const
	{
		return x < y;
	}
};

• 利用模板比较greater

template<class T>
struct greater//用于  > 的比较
{
	bool operator()(const T& x, const T& y) const
	{
		return x > y;
	}
};

 ③、测试： 

//测试less
less<int> LessFunc;
cout << LessFunc(1, 2) << endl;//1
//测试greater
greater<int> GreaterFunc;
cout << GreaterFunc(1, 5) << endl;//0

为什么说仿函数又叫函数对象？

比如测试代码中的LessFunc，它是个对象，但他调用时直接写为LessFunc(1, 2)，就像一个函数在调用，但他并不是函数，调用的本质是lessFunc.operator()(1, 2)，所以仿函数即对象可以像函数一样使用

④、algorithm中的sort

 sort的第三个参数使用到了仿函数，其为仿函数的对象

第一个参数和第二个参数都是迭代器，第三个参数是仿函数，其默认值为less

升序：less <       降序：greater >  

注：第三个参数不传默认是less，即排升序

#include<iostream>
#include<algorithm>
using namespace std;

void test_sort()
{
	vector<int>v;
	v.push_back(1);
	v.push_back(4);
	v.push_back(5);
	v.push_back(2);
	//升序，less <
	sort(v.begin(), v.end());

	for (auto e : v)
	{
		cout << e << " ";
	}
	cout << endl;

	//降序 greater >
	// 写法一、定义一个对象 
	//greater<int> gt;
	//sort(v.begin(), v.end(),gt);
	//写法二、匿名对象（更推荐）
	sort(v.begin(), v.end(), greater<int>());//greater<int>()是匿名对象
	for (auto e : v)
	{
		cout << e << " ";
	}
	cout << endl;

}

int main()
{
	//test_priority_queue();
	test_sort();

	return 0;
}

二、priority_queue(优先级队列)

1、概念：

 优先级队列与queue不一样，它是优先级高的先走（默认情况是大的数优先级高，但如果想要小的优先级高，如何操作？-> 用仿函数），它的底层其实是堆中的大堆，不用数组的原因是堆的效率高

2、使用：

 queue的头文件同时包含了priority_queue和queue，所以用priority_queue直接#include<queue>即可，

注：容器适配器都不支持迭代器遍历，因为他们通常都包含一些特殊性质，如果支持迭代器随便遍历，那他们无法很好的保持他的性质，这里priority_queue也是容器适配器，故不支持迭代器

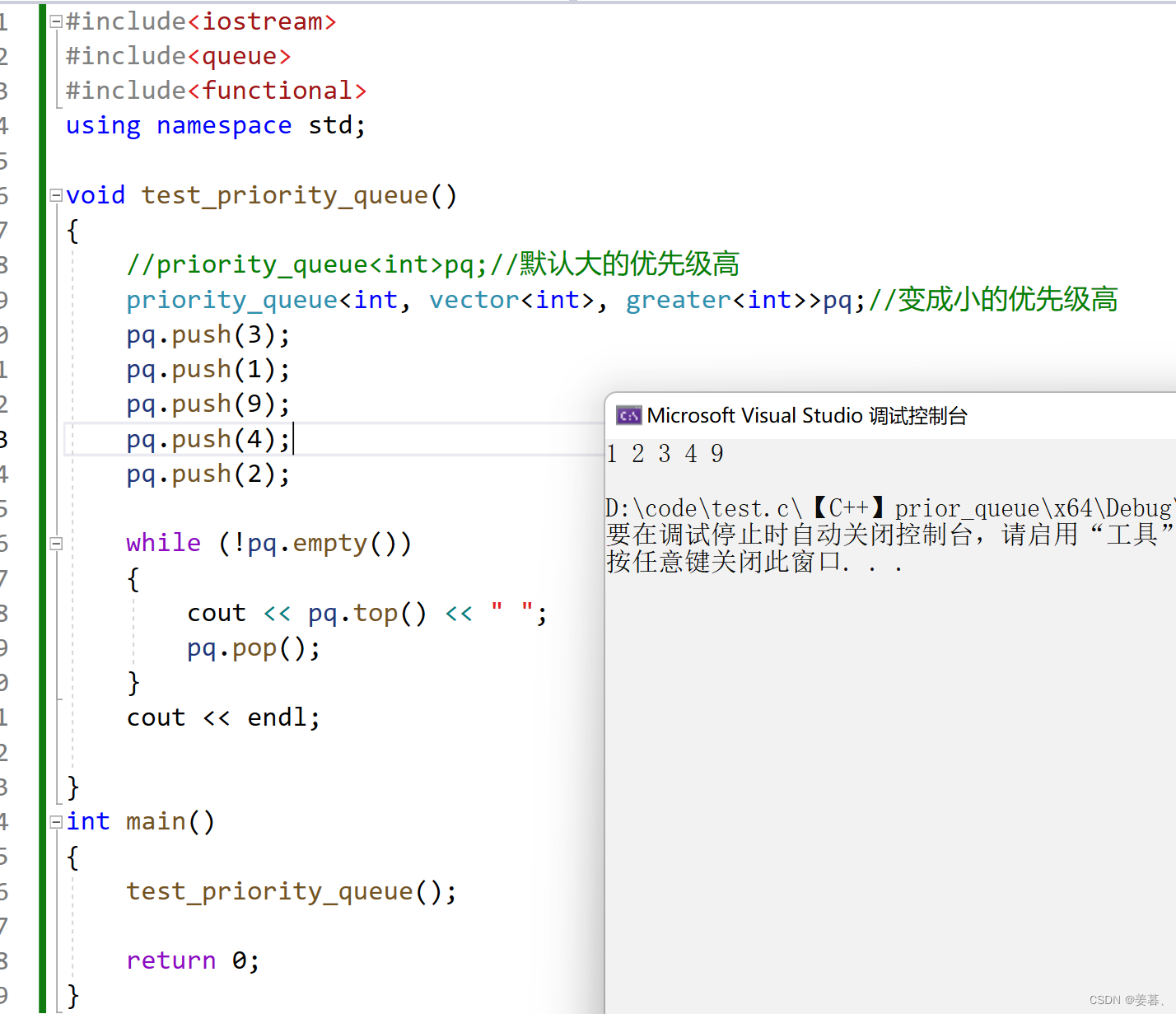
由运行结果可知，默认情况下是大的数优先级高，若要使小的优先级高，需要调用仿函数，priority_queue的第一个参数是值的类型，第二个参数是内部的适配容器，第三个参数是仿函数，而仿函数要引头文件 #include<functional>（仿函数下文会讲）

下面给出使小的优先级高的代码：

3、数组中第K个最大元素

基本介绍后我们来做一道可用priority_queue实现的题（三种解法）

 法一、优先级队列实现

class Solution {
public:
	int findKthLargest(vector<int>& nums, int k) {
		priority_queue<int> pq;
		for (auto e : nums)
			pq.push(e);//把所有数据插入到pq中

		while (--k)
			pq.pop();//执行了k-1次的删除

		return pq.top();//剩下的一个元素就是第k大的
	}
};

时间复杂度：O（N*logN）

解释：优先级队列建堆：O（N），插入数据push：O（N*logN），删除数据pop：O（k*logN），三者相加，综上时间复杂度为O（N*logN）

空间复杂度：O（N）

因为开辟的优先级队列的空间，故为O（N）

法二、用算法中的sort实现

class Solution {
public:
	int findKthLargest(vector<int>& nums, int k) {
		//解法二：
		sort(nums.begin(), nums.end());//不用仿函数的话默认情况下排升序
		return nums[nums.size() - k];//返回倒数第二个即可
	}
};

时间复杂度：O（N*logN）

因为sort的底层是快排，快排的时间复杂度：O（N*logN）

空间复杂度：O（1）

现假设N是一千万，K是100，这时时间空间消耗都很大，怎么优化？建堆实现

法三、用堆实现（类似于TopK问题）

这个其实跟TopK问题差不多，只不过这里是找第k个大的那个，故建有k个数的小堆（那么这k个数最后都会变成前k大的数），只要比堆顶大，就能进入堆中

下面是我之前写过的TopK求解思路（推荐看，便于理解）：

【数据结构】---TopK问题_姜暮、的博客-CSDN博客

class Solution {
public:
	int findKthLargest(vector<int>& nums, int k) {
		//解法三：
		//利用仿函数建小堆，因为默认情况下优先级队列是建大堆
		priority_queue<int, vector<int>, greater<int>>minHeap;
		size_t i = 0;
		for (; i < k; ++i)
			minHeap.push(nums[i]);//先入k个数据（数据是什么无所谓）

        //使堆中是前k大的数据
		for (; i < nums.size(); ++i)
		{
			if (nums[i] > minHeap.top())
			{//比堆顶大的就替换堆顶
				minHeap.pop();
				minHeap.push(nums[i]);
			}
		}

		return minHeap.top();//因为是小堆，则堆顶即k个数中它是最小的，因为k个数是前k大的
	}
};

时间复杂度：O（N*logK）

解释：优先级队列建堆：O（N），k个数据的push：O（logk），因为本质是向上调整法≈k次，比较的过程：O（N*2*logk）三者相加，综上为O（N*logk） 

空间复杂度：O（K）

当N很大的时候，这个方法的效率是非常好的

4、priority_queue的模拟实现

向上调整法和向下调整法为什么需要用到仿函数？

因为堆分大堆和小堆，向上和向下调整法对于大小堆的实现只有一个符号的差别，难道写两份调整法？不够好，故用仿函数实现，使大堆和小堆都能用一份代码

若参数是less，会建大堆,排升序
若参数是greater，会建小堆，排降序

为什么无需数组建堆？

之前讲的是已经存在数据的数组，他现有的顺序很可能不符合大堆或小堆的性质，故要数组建堆，这样插入删除等操作才能很好进行，而这里的模拟实现，一开始就没有数据，故不用建堆，它是每插入一个数据，调用向上调整法，删除数据，调用向下调整法，不断地插入和删除，还能使其保持堆的性质 

 priority_queue.h:

#pragma once
#include<iostream>
#include<assert.h>
#include<vector>
#include<queue>
#include<functional>
#include<algorithm>

namespace mz
{
	//仿函数/函数对象 --- 对象可以像调用函数一样去使用
	template<class T>
	struct less
	{
		//()运算符重载--用于比较大小
		bool operator()(const T& x, const T& y) const
		{
			return x < y;
		}
	};
	template<class T>
	struct greater
	{
		//()运算符重载--用于比较大小
		bool operator()(const T& x, const T& y) const
		{
			return x > y;
		}
	};

	//优先级队列
	template<class T, class Container = vector<T>, class Compare = less<T>>
	class priority_queue
	{
	public:
		//向上调整算法
		void AdjustUp(int child)
		{
			Compare com;//创建一个仿函数对象
			int parent = (child - 1) / 2;
			while (child > 0)
			{
				if (com(_con[parent], _con[child]))//利用仿函数建大堆或小堆
				{
					swap(_con[parent], _con[child]);
					//更新child和parent
					child = parent;
					parent = (child - 1) / 2;
				}
				else
				{
					//此时不需要调整，直接break
					break;
				}
			}
		}
		//向下调整算法
		void AdjustDown(int root)
		{
			int parent = root;
			int child = parent * 2 + 1;
			Compare com;//仿函数
			while (child < _con.size())
			{
				if (child + 1 < _con.size() && com(_con[child],_con[child + 1]))
				{//利用仿函数，区别大小堆向下调整法的不同之处
					child++;
				}
				if (com(_con[parent], _con[child]))
				{
					swap(_con[parent], _con[child]);
					//更新child和parent
					parent = child;
					child = parent * 2 + 1;
				}
				else
				{
					//此时不需要调整，直接break
					break;
				}
			}
		}
		//插入数据
		void push(const T& x)
		{
			_con.push_back(x);
			//每插入一个数据，都要向上调整建堆
			AdjustUp((int)_con.size() - 1);
		}
		//删除数据
		void pop()
		{
			assert(!_con.empty());//删除的前提：不为空
			swap(_con[0], _con[_con.size() - 1]);//交换头尾数据
			_con.pop_back();//删除最后一个数据
			AdjustDown(0);//从根部向下调整建堆
		}
		//取堆顶数据
		const T& top()
		{
			return _con[0];
		}
		//获取size有效数据个数
		size_t size()
		{
			return _con.size();
		}
		//判空
		bool empty()
		{
			return _con.empty();
		}
	private:
		Container _con;
	};
}

 test.cpp:

using namespace std;
#include"priority_queue.h"


void test_priority_queue()
{
	//priority_queue<int>pq;//默认大的优先级高
	mz::priority_queue<int, vector<int>, greater<int>> pq;//变成小的优先级高
	pq.push(3);
	pq.push(1);
	pq.push(9);
	pq.push(4);
	pq.push(2);

	while (!pq.empty())
	{
		cout << pq.top() << " ";
		pq.pop();
	}
	cout << endl;

}

int main()
{
	test_priority_queue();
	//test_sort();

	return 0;
}

运行结果：

 

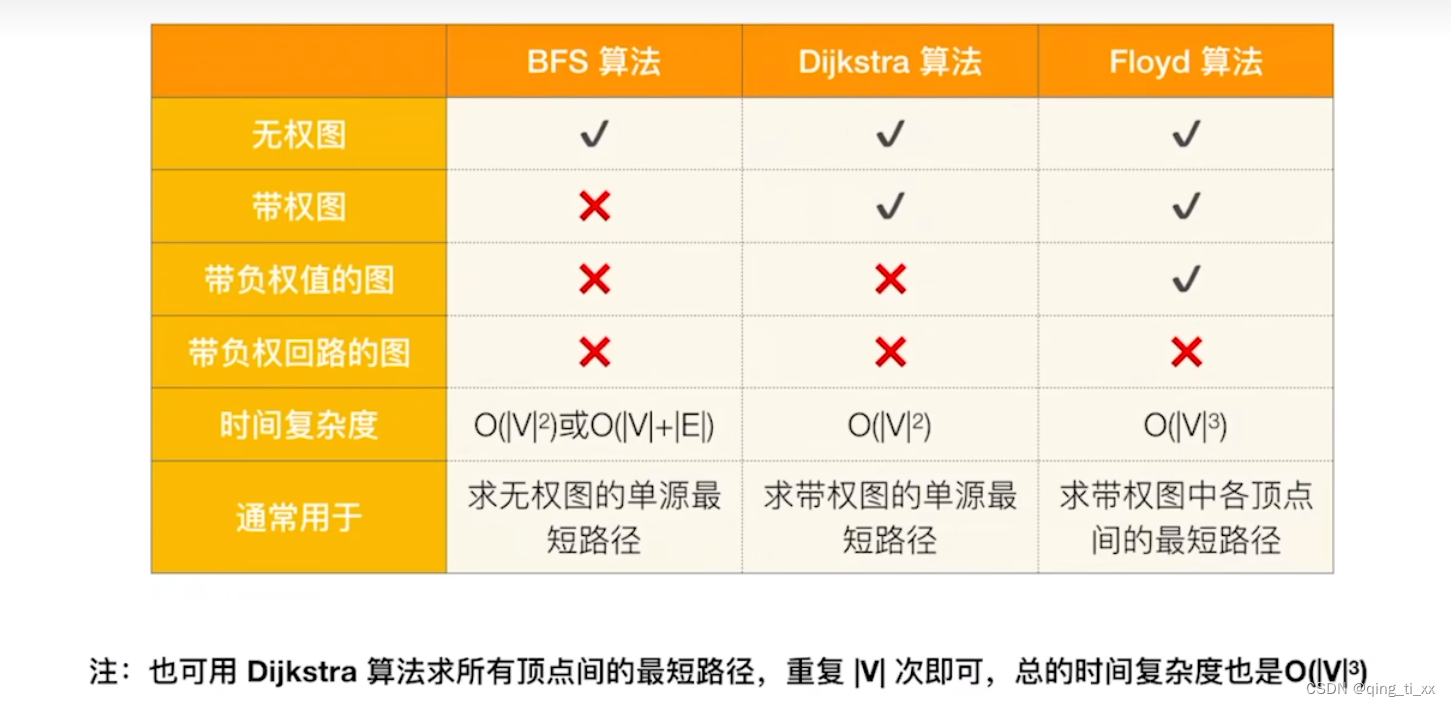
 STL的大体总结：