目录

一、BFS算法（单源最短路径）

（1）介绍：

（2）例子：

二、Dijkstra算法（单源最短路径）

（1）介绍：

（2）例子：

第一步

第二步

第三步

第四步

最后

三、Floyd算法（各个顶点间的最短路径）

代码：

例子：

第一步

第二步

第三步

第四步

结论：

注意★★★★★：

---

一、BFS算法（单源最短路径）

（1）介绍：

这个算法是计算所有路径权值为1的图的最短路径。

（2）例子：

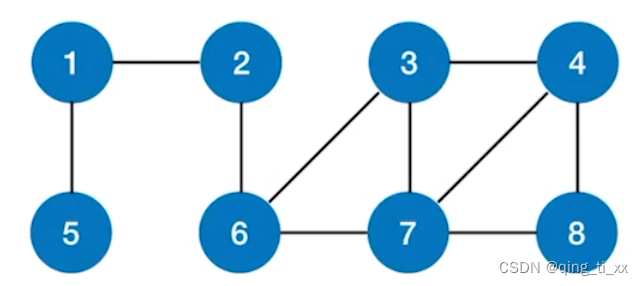
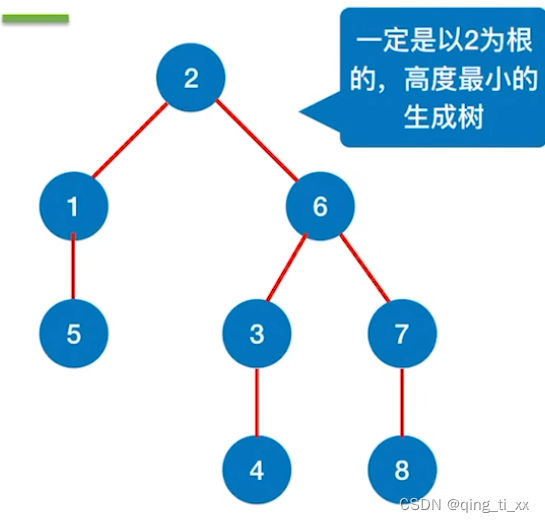
从结点2出发，使用宽度优先遍历，获得最小生成树，树的层数也就是到达该结点的最短路径。

二、Dijkstra算法（单源最短路径）

（1）介绍：

 找到有向有权图的最短路径。

（2）例子：

从V0出发找到最短路径

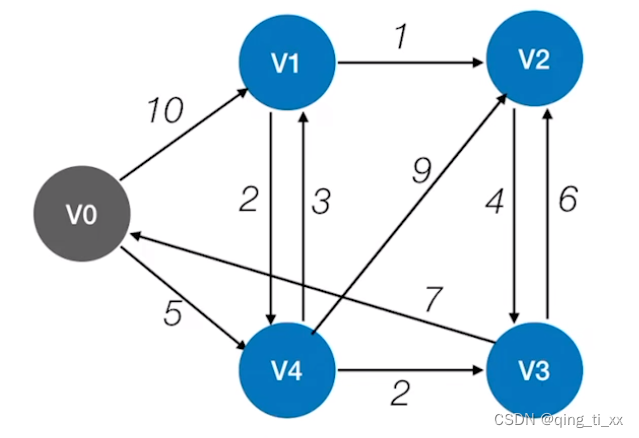
第一步

我们需要创建3个数组，分别存储

该结点是否已找到最短路径

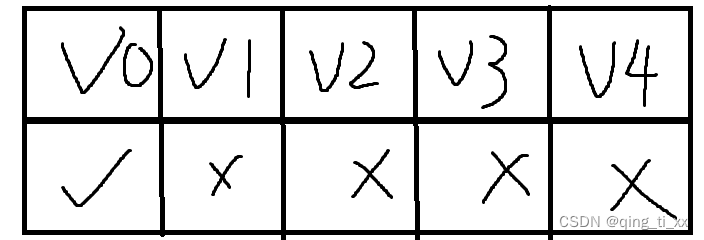
最短路径的长度

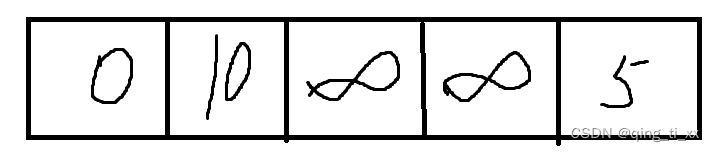
路径上的前驱

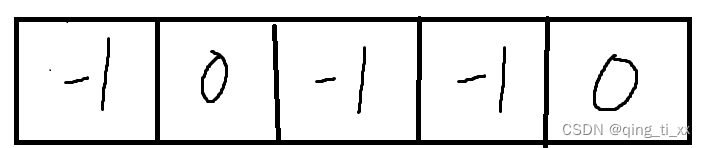
第二步

找最短的路径长度，并移动到该结点

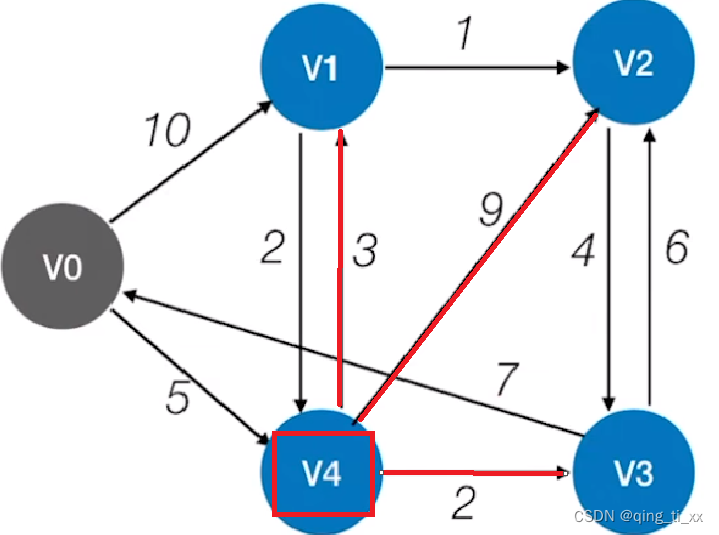
从该V4结点我们可以找到通往V4的路径长度为5（前驱为V0），

通往V1的新路径长度为3+5=8（前驱为V4），

还有V2的路径5+9=14（前驱为V4），V3的路径5+2=7（前驱为V4），更新数组。

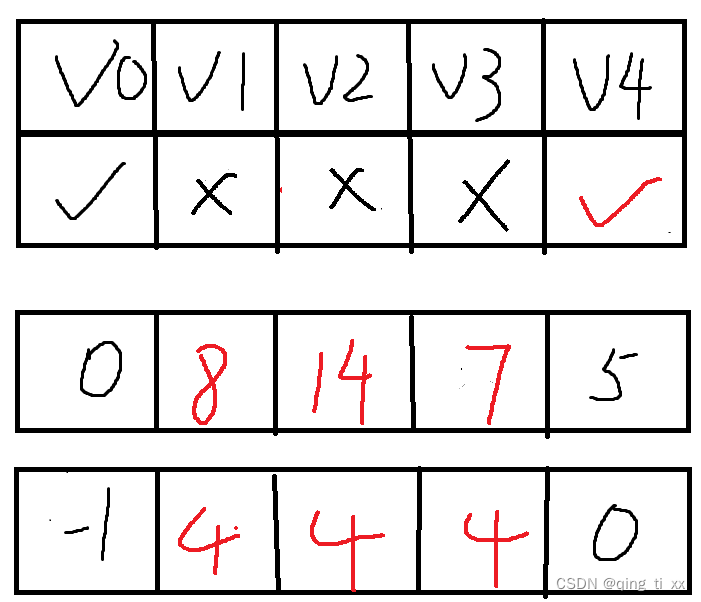
第三步

遍历该结点是否已找到最短路径的数组，找到它们路径的长度最短的结点。

在上图中，最短结点为V3，于是，我们将移动到V3，并将V3设置为已找到最短路径。

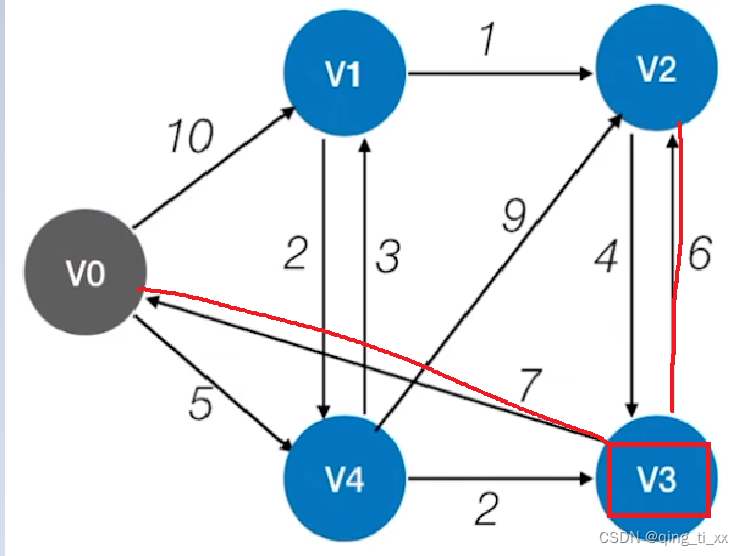
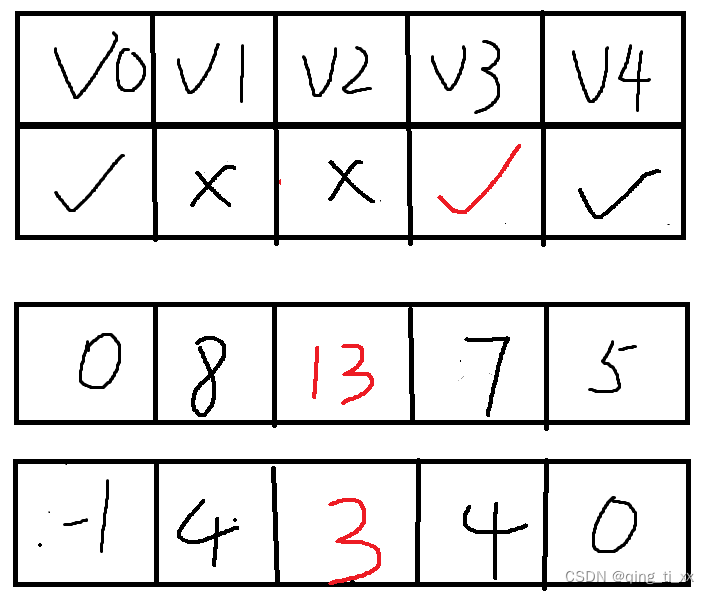
我们找到了前往V0的新路径，但是V0已经找到了最短路径。所以跳过。

还找到了前往V2的新路径，路径长度为7+6=13，用它与14比较，发现小于14，所以更新数组。

第四步

遍历该结点是否已找到最短路径的数组，找到它们路径的长度最短的结点。

在上图中，最短结点为V1，于是，我们将移动到V1，并将V1设置为已找到最短路径。

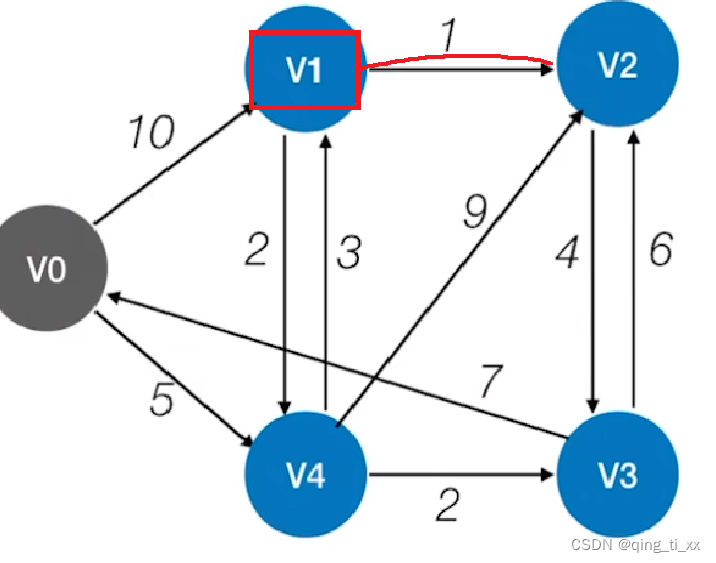
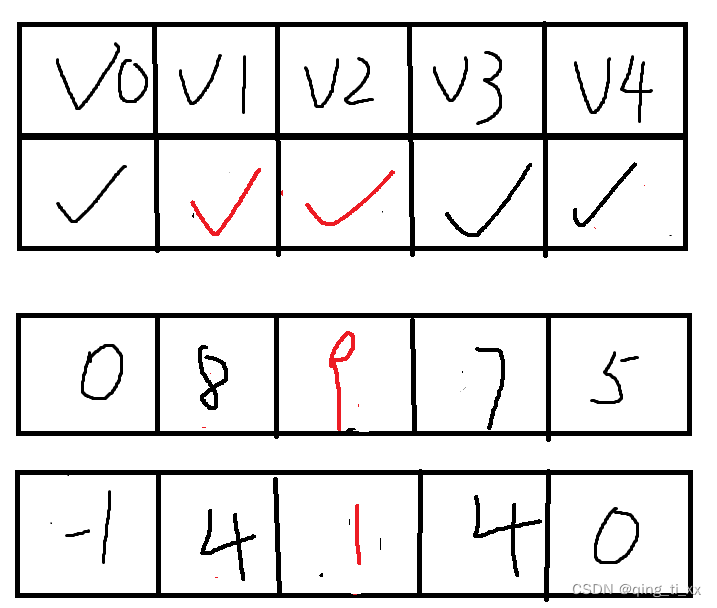
我们找到了前往V2的新路径，路径长度为8+1=9，前驱为V1。

更新数组，发现V2已经是最后一个结点，直接设置为true。

最后

我们可以通过这个数组任意结点找到到达V0的最短路径。

例如V2，L=9，v2 <- v1 <- v4 <- v0

时间复杂度：O()

注意：Dijkstra算法不适用于有负权值的带权图。

三、Floyd算法（各个顶点间的最短路径）

代码：

时间复杂度，O()

空间复杂度，O()
 

例子：

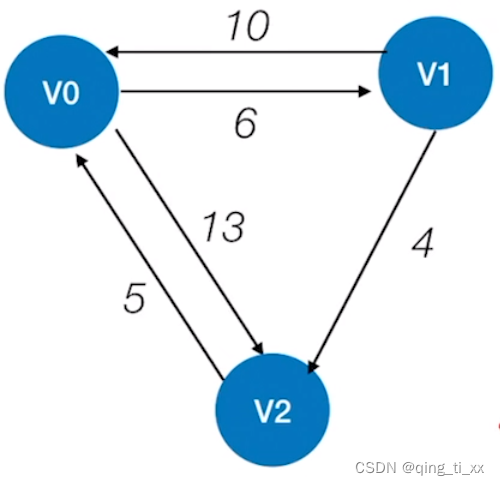
第一步

根据所给的图，不允许中转，做出相应的距离矩阵。

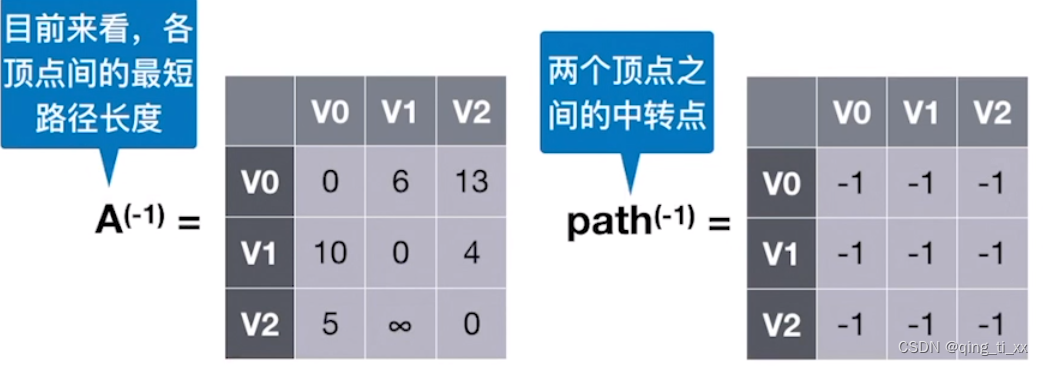
第二步

（1）加入V0，使路径允许在V0进行中转。

（2）我们发现，加入V0后，V2有新的路径指向V1，长度为5+6=11，与原来的进行比较，11<∞，于是更新矩阵A[V2][V1]的值为11，path[V2][V1]为0（V0为中转点）

（3）V1有新的路径指向V2，但是10+13>4，所以不更新。

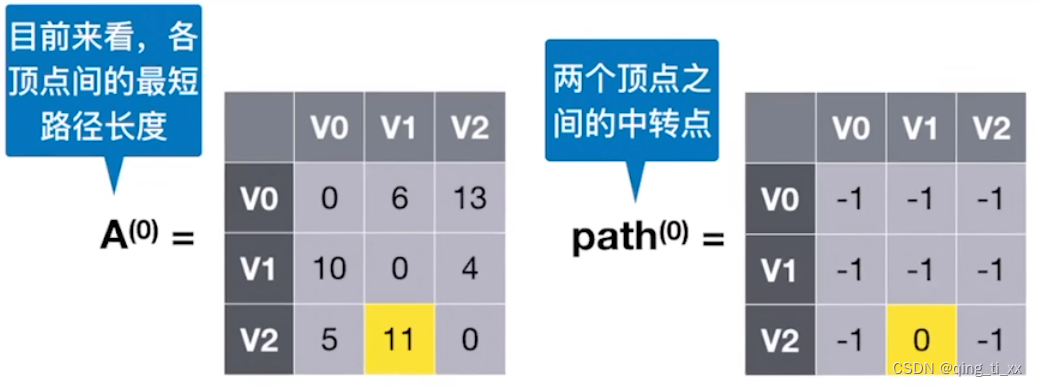
第三步

（1）加入V1，使路径允许在V0，V1进行中转。

（2）我们发现，加入V1后，V0有新的路径指向V2，长度为4+6=10，与原来的进行比较，10<13，于是更新矩阵A[V0][V2]的值为10，path[V0][V2]为1（V1为中转点）

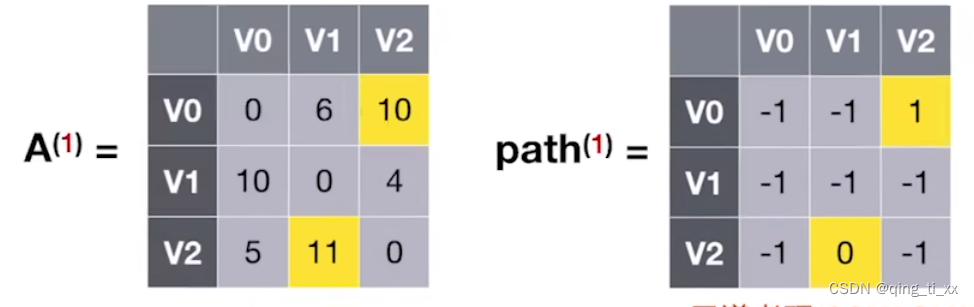
第四步

（1）加入V2，使路径允许在V0，V1，V2进行中转。

（2）我们发现，加入V2后，V1有新的路径指向V0，长度为4+5=9，与原来的进行比较，9<10，于是更新矩阵A[V1][V0]的值为9，path[V1][V0]为2（V2为中转点）

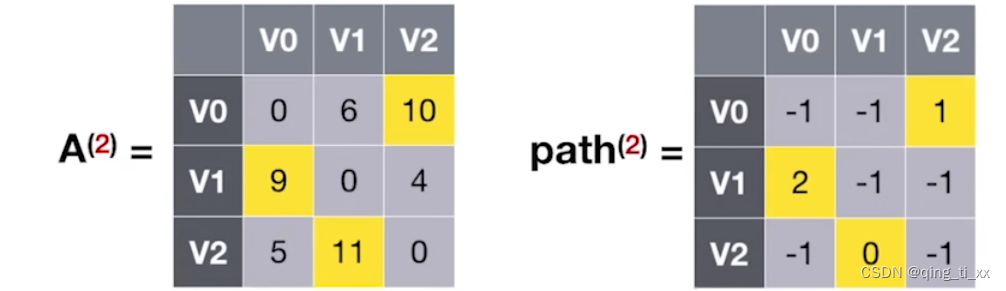
结论：

注意★★★★★：

Floyd算法可以用于负权值带权图；

Floyd算法不能解决带有“负权回路"的图（有负权值的边组成回路)，这种图有可能没有最短路径；