0、论文基本信息

DMP经典论文
论文题目：Learning and Generalization of Motor Skills by Learning from Demonstration
会议名称：2009 ICRA
论文作者：Peter Pastor, Heiko Hoffmann, Tamin Asfour and Stefan Schaal

作者简介：Stefan Schaal是美国University of Southern California教授，之前也介绍过，是DMP的提出者，非常厉害的老师，在Youtube上看过他的报告，学术气质一流，主要做运能技能的学习，如模仿学习和强化学习。知乎上的大佬也表示，经过Stefan Schaal教授点拨的学生或合作的同事都走向了人生巅峰，如Auke Jan Ijspeert，Aude Billard，Sethu Vijayakumar，Jan Peters（Jens Kober是Jan Peters的学生），欧洲很多有影响力的机器人+机器学习实验室都和Stefan Schaal有着千丝万缕的联系。

题目：从示教中学习和泛化运动技能
摘要：作者提供了一种从人类演示中学习机器人运动技能的通用方法。为了表示观察到的运动，学习了一个非线性微分方程，使其可以再现这一运动。基于这种表示，作者根据任务和上下文（例如，抓握、放置和释放）标记每个记录的动作来构建动作库。作者提出的微分方程可以通过将方程中的起始和目标参数调整为运动所需位置值来简单地实现泛化。对于对象操作，作者介绍了提出的框架如何扩展到控制抓手方向和手指位置。改方法的可行性在仿真中以及在Sarcos灵巧的机械臂上得到了验证。该机器人学习了pick and place操作和倒水任务，并可以将这些任务推广到新的情况。

一、引言

这里只提炼核心内容：机器人只有易于编程，才能广泛服务于人类。易于编程可以通过示教学习实现。示教学习的三个问题需要解决，1，对应问题，即人类和机器人的关节和连杆不匹配。2，泛化，即人类无法演示机器人支持的每一个动作，所以需要进行泛化。如果演示的动作可以推广到其他环境中，比如不同的目标位置，那么通过演示进行学习是可行的。3，抵抗扰动的鲁棒性，即，在未知的动态环境中，精确复现观察到的动作是不切实际的，因此在这个环境中可能会突然出现障碍物。

为了解决这些问题，作者提出了一个基于DMP框架的模型，在这个框架下，任何记录的运动，都可以表示为一系列微分方程。用微分方程表示运动的优点是1，可以自动矫正扰动的影响（通过耦耦合项），2，仅改变目标点参数，其他不变，就可到达一个新的位置，具有泛化能力。本文提出了新的DMP公式，以解决传统DMP在更改目标位置参数时遇到的几个问题。

作者在末端执行器空间表示运动轨迹以解决问题1的对应问题，对于抓取和放置等目标操作，除了末端位置，我们还需要控制抓手的姿态和手指的位置（张开和闭合程度），DMP框架允许结合末端运动和任何附加的自由度，因此，可以直接添加四元数表示的抓手姿态和手指位置。在机器人演示中，作者使用解析的运动速率逆运动学将末端执行器位置和抓手姿态映射到适当的关节角度。

为了处理复杂的运动，可以使用上述DMP框架来构建运动基元库，随后可以通过排序来组成更加复杂的运动。例如，运动基元库可能包含抓取、放置和释放动作。这些动作中的每一个都是从人类演示中记录下来的，随后由一个微分方程表示，并相应地标记。对于在桌子上移动对象，需要一个抓取-放置-释放序列，并从库中调用相应的基元。由于每个动态运动基元的泛化能力，可以仅基于所演示的三个运动，将物体放置在桌子上任意位置。

二、动态运动基元及其改进

A. 传统DMP

一维运动表示为受外力项扰动的线性弹簧系统：
公式1和公式2
$\begin{array}{rl}\tau \dot{v}& =K(g-x)-Dv+\left(g-x_0\right)f(s)\\ \tau \dot{x}& =v\end{array}$
这里的DMP公式和平常看到的可能不一样，这里只是强调了弹簧特性，并不影响。$x$和$v$分别是系统的位置和经过时间因子$\tau$缩放后的速度，$x_0$和$g$分别为运动的起点和终点。$K$是弹性常数$D$是阻尼常数，选择合适的$K$和$D$以保证系统达到临界阻尼状态。$f$是非线性函数，可以通过LWR（Locally Weighted Regression，局部加权回归）学习其参数，以生成任意复杂的运动。非线性函数$f$定义如下：
$\begin{array}{r}f(s)=\frac{{\sum }_i{w}_i{\psi }_i(s)s}{{\sum }_i{\psi }_i(s)}\end{array}$
其中，${\psi }_i=exp(-h_i(s-c_i{)}^2)$为高斯基函数，$c_i$为高斯基函数中心，$h_i$为高斯基函数宽度，$w_i$为可调权重。函数$f$不直接依赖时间$t$，而是相变量$s$的函数，$s$随着运动的进行，从1到到0单调递减，相变量$s$满足公式：
公式4：
$\begin{array}{r}\tau \dot{s}=-\alpha s\end{array}$
其中$\alpha$是一个预定义常数，上述公式通常被称为正则系统（canonical system）

使用这些方程表示运动的优势：
a.保证收敛到目标点$g$，因为$f(s)$会在运动的末端消失；
b.可以学习权重参数$w_i$以生成任意期望的光滑轨迹；
c.方程是空间和时间不变的，即，对于起点、重点和时间缩放的变化，运动是自相似的，而不需要改变权重$w_i$
解释：这里意思应该是泛化能力，给定任意起始点，运动轨迹总是和示教轨迹相似，不需要对微分方程做任何改变。
d.由于方程的固有吸引子动力学，该公式产生的运动对扰动是鲁棒的。

为了从示教中学习运动，首先，需要记录示教轨迹$x(t)$，以及他的导数$v(t)$和$\dot{v}(t)$，第二，对正则系统进行合并，即，为适当的时间缩放因子$\tau$计算$s(t)$。因此：
$\begin{array}{r}{f}_{target}(s)=\frac{-K(g-x)+dv+\tau \dot{v}}{g-x_0}\end{array}$
这里$f_{target}$只是通过公式得到的，另外$f$还可以表示为多个高斯基函数的组合。因此为了求权重$w_i$，可以转化为求解一个线性回归问题$J={\sum }_s(f_{target}(s)-f(s){)}^2$。有了权重$w_i$，给定不同起始点，便可生成与示教轨迹相同趋势的运动。

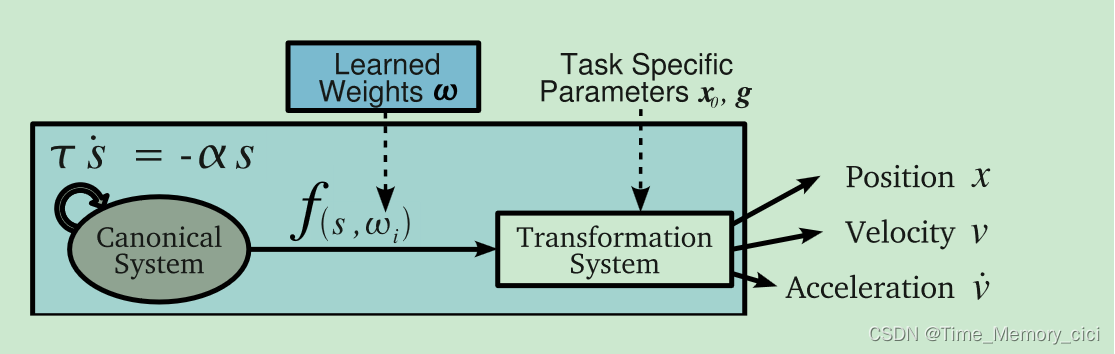
图1.一维DMP的原理图：正则系统驱动非线性函数f，该函数扰动变换系统以计算期望的运动。

B. 泛化到新的目标

经典DMP方法泛化到新的目标点时有三个缺点：1，如果运动的起点$x_0$和终点$g$一样，则公式1中的非线性项不能驱动系统离开起点$x_0$，这将导致系统停留在初始点$x_0$。2、如果$g-x_0$接近零，函数$f$的缩放$g-x_0$是有问题的。在这里，$g$的微小变化可能会导致巨大的加速度，这可以打破机器人的极限。3、每当一个动作适应一个新的目标$g_{new}$，使得$(g_{new}-x_0)$与$(g_{original}-x_0)$相比改变了它的符号时，所产生的泛化就会被镜像(想象一下sin曲线)。因此，作为本论文实验中的一个例子，在桌子上放置动作的起点和终点位置大致相同；因此，最初的DMP公式不适合将这种运动适应新的目标位置。

C. 改进的DMP

本文提出改进的DMP以解决上述问题，而且保留DMP的有优点，改进后的DMP如下：

$\begin{array}{rl}\tau \dot{v}& =K(g-x)-Dv-K(g-x_0)s+Kf(s)\\ \tau \dot{x}& =v\end{array}$
其中$f(s)$和经典DMP中的定义一致，正则系统有和前面公式4一致。与经典DMP的重要不同是非线性函数$f(s)$不再乘$(g-x_0)$，改进DMP的第三项$K(g-x_0)s$用于避免运动开始时的跳跃，学习和传播DMP和之前步骤是一样的，只是目标函数$f_{target}$是根据以下公式计算：
$\begin{array}{r}{f}_{target}(s)=\frac{\tau \dot{v}+Dv}{K}-(g-x)+(g-x_0)s\end{array}$

D. 避障