文章目录
- 一、简介
- 二、时间复杂度
- 三、非线性时间比较类排序
- 冒泡排序(Bubble Sort)
- 排序过程
- 代码实现
- 步骤拆解演示
- 复杂度
- 选择排序(Selection Sort)
- 排序过程
- 代码实现
- 步骤拆解演示
- 复杂度
- 插入排序(Insertion Sort)
- 排序过程
- 代码实现
- 步骤拆解演示
- 复杂度
- 二分插入排序(Binary Insertion Sort)
- 代码实现
- 希尔排序(Shell Sort)
- 排序过程
- 代码实现
- 步骤拆解演示
- 复杂度
- 归并排序(Merging Sort)
- 排序过程
- 代码实现
- 步骤拆解演示
- 复杂度
- 快速排序(Quick Sort)
- 排序过程
- 代码实现
- 步骤拆解演示
- 复杂度
- 堆排序(Heap Sort)
- 排序过程
- 代码实现
- 步骤拆解演示
- 复杂度
- 四、线性时间非比较类排序
- 基数排序(Radix Sort)
- 排序过程
- 代码实现
- 步骤拆解演示
- 复杂度
- 计数排序(Counting Sort)
- 排序过程
- 代码实现
- 步骤拆解演示
- 复杂度
- 桶排序(Bucket Sort)
- 排序过程
- 代码实现
- 步骤拆解演示
- 复杂度
- 五、Java中Arrays.sort()用的什么排序算法
- Dual-Pivot Quick Sort(双轴快速排序)
- 流程图
- Tim Sort
- run
- minRun
- 压栈
- 合并
- 流程总结
- 复杂度
一、简介
常见的排序算法有十种,可以分为以下两大类:
-
非线性时间比较类排序:通过比较来决定元素间的相对次序,由于其时间复杂度不能突破O(n log n),因此称为非线性时间比较类排序
-
线性时间非比较类排序:不通过比较来决定元素间的相对次序,它可以突破基于比较排序的时间下界,以线性时间运行,因此称为线性时间非比较类排序
二、时间复杂度
时间复杂度从小到大:
O(1) < O(log n) < O(n) < O(n log n) < O(n^2) < O(n^3) < O(2^n) < O(n!) < O(n^n)
前四个效率比较高,中间两个一般般,后三个比较差
三、非线性时间比较类排序
冒泡排序(Bubble Sort)
**循环遍历多次,每次从前往后把大元素往后调,每次确定一个最大(最小)元素,循环多次后达到排序效果。**因为在排序过程中,较大(或较小)的元素会逐渐向列表的一端"冒泡",所以得名:冒泡排序
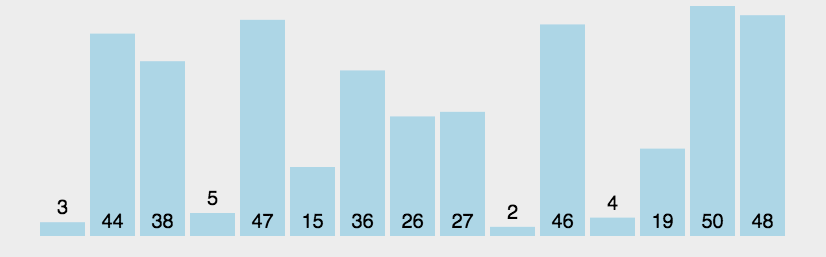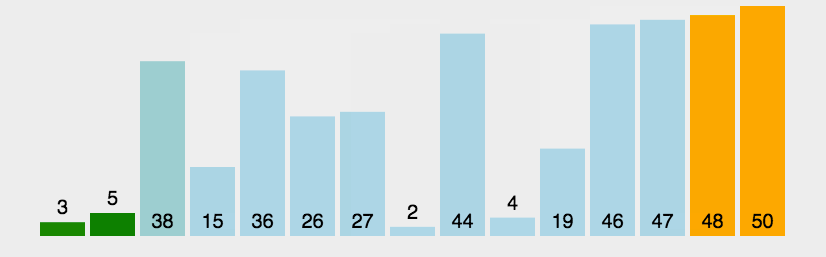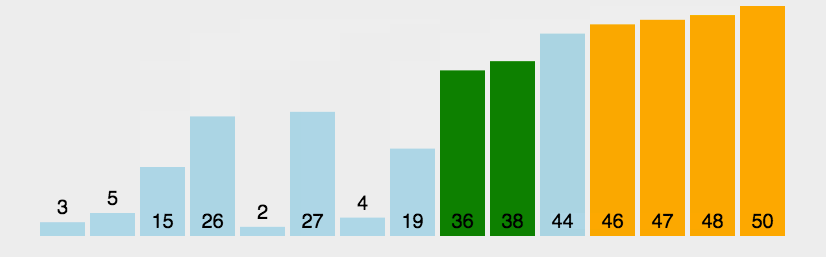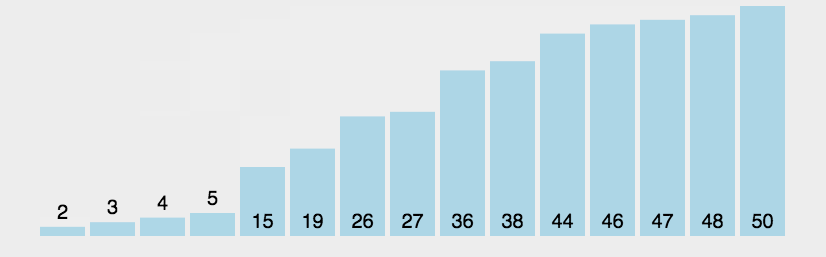
排序过程
- 比较相邻元素,如果前者大于后者,就交换两个元素的位置。对每一对相邻元素都做这样的操作,从开始第一对到结尾的最后一对。例如:一个长度是n的数组,先比对1、2两个位置,再比对2、3两个位置,直到比对完n-1、n两个位置,这时候,我们认为完成了一次冒泡,最后一个元素一定是最大的。
- 然后不断重复第1步的操作,因为最后一个元素一定是最大的,不需要再操作最后一个元素了,可以当最后一个元素不存在,数组长度变成了n-1,每一次冒泡,结尾都会排好一个元素,下一次冒泡需要操作的元素就少一个,一直重复直到完成排序
代码实现
public static void bubbleSort(int[] arr) {
if (arr == null || arr.length == 0) {
return;
}
for (int i = 0; i < arr.length - 1; i++) {
//这里减i的原因是,每次外循环会在最后排好一个元素,下次循环时就可以少比较一个元素
for (int j = 0; j < arr.length - 1 - i; j++) {
//如果前者大于后者,交换两者位置
if (arr[j] > arr[j + 1]) {
int temp = arr[j];
arr[j] = arr[j + 1];
arr[j + 1] = temp;
}
}
}
}
步骤拆解演示
我们以 [3, 44, 38, 5, 47, 15, 36, 26, 27, 2, 46, 4, 19, 50, 48] 为例,初始如下图所示:

从第一个元素开始比较大小,如果前者大于后者,就调换两个位置,先比较3和44,发现3小于44,不动,再比较44和38,发现44大于38,所以调换两者位置,因为44和38换了位置,所以下面比较44和5,发现44大于5,再调换两者位置,一直比对到最后,如下图所示:

这样就完成一次冒泡,50这个元素就排好了,下面再以同样的方法,只不过排到倒数第二个元素,每重复一次,排好一个元素,15次冒泡排序后就完成排序了,如下图所示:
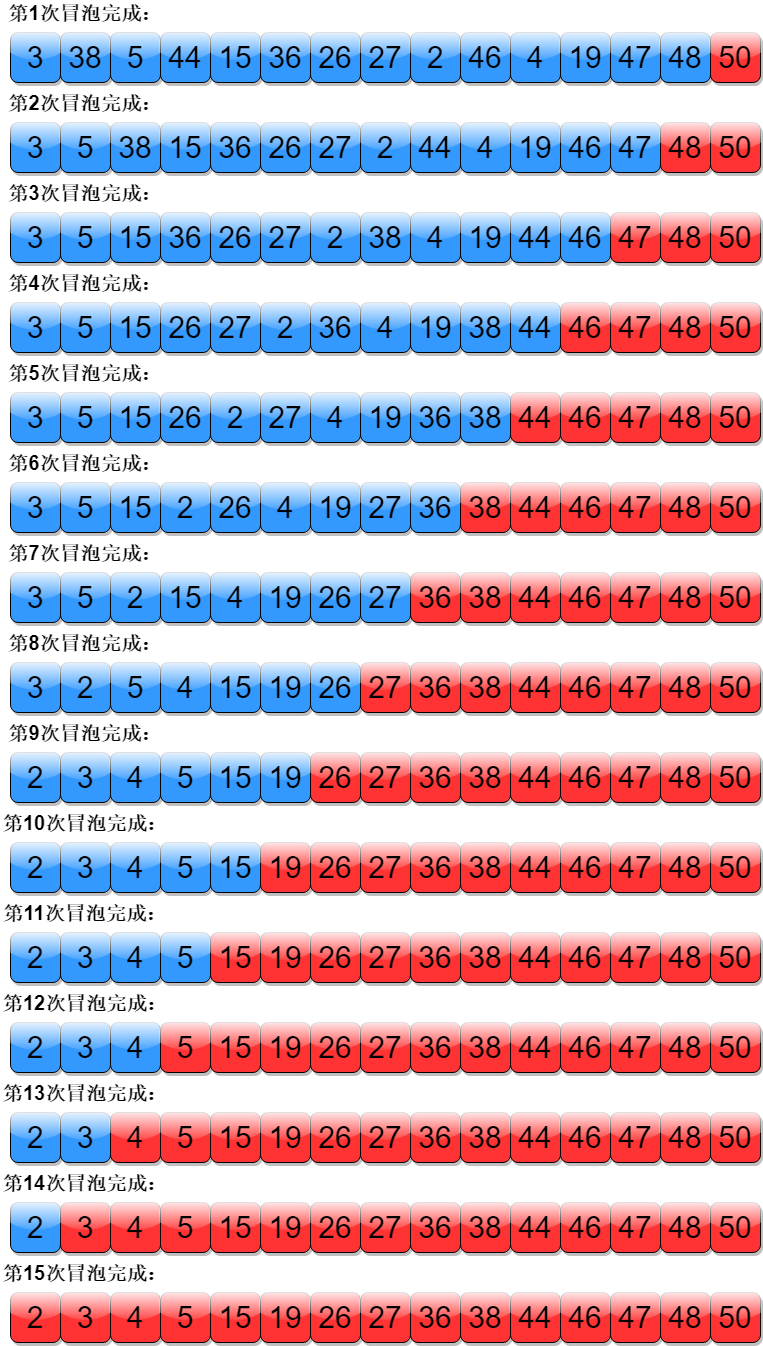
其实在第9次冒泡排序的时候,就已经完成所有的排序,所以冒泡排序还可以优化一下,比如增加一个标识来记录每次冒泡有没有元素交换,如果没有,就说明已经排好了,可以直接结束排序了。或者记录上一次最后交换的位置,作为下一次比较的终点,因为在这个位置之后的元素已经是有序的,不需要再进行比较了(比如第二次冒泡的最后一次交换是在倒数第4个位置,第三次冒泡的时候,比较到这个位置就可以了)。
复杂度
| 平均时间复杂度 | 最好情况 | 最坏情况 | 空间复杂度 |
|---|---|---|---|
| O(n^2) | O(n) | O(n^2) | O(1) |
最好的情况下,一趟扫描就可以完成排序,复杂度为O(n),最坏的情况就是每次都需要交换,复杂度为O(n2),总体平均复杂度为O(n2),因为没有占用额外空间,所以空间复杂度是O(1)。
选择排序(Selection Sort)
每次从待排序的数据元素中选出最小(或最大)的一个元素,存放在序列的起始位置,然后再从剩余未排序的元素中继续寻找最小(或最大)的元素,放到已排序序列的末尾。以此类推,直到所有元素都排序完毕
排序过程
- 先排第1个元素,拿第1个元素和后面所有的元素比较,如果找到比第1个元素小且最小的那个元素,就和第1个元素交换,这样第1个元素就是最小的
- 因为第1步已经排好了第1个元素,所以可以跳过第1个元素了,拿第2个元素和后面所有元素比较,找到最小的元素和第2个交换,这样第2个元素就排好了,下面是第3个元素…,一直重复这个操作,直到完成排序
代码实现
public static void selectSort(int[] arr) {
if (arr == null || arr.length == 0) {
return;
}
for (int i = 0; i < arr.length - 1; i++) {
//设定当前位置为最小值
int min = i;
//遍历剩余未排序的部分,如果找到比当前最小值更小的元素,则更新最小值的位置
for (int j = i + 1; j < arr.length; j++) {
if (arr[min] > arr[j]) {
min = j;
}
}
if (min != i) {
//将最小值与当前位置交换
int temp = arr[min];
arr[min] = arr[i];
arr[i] = temp;
}
}
}
步骤拆解演示
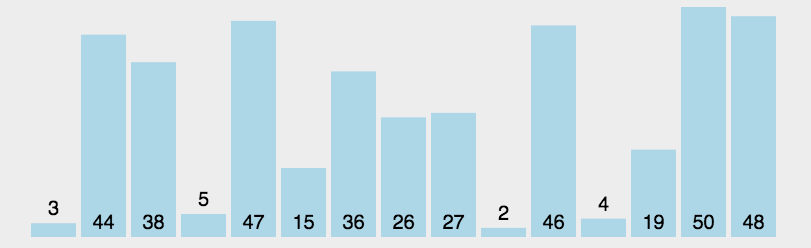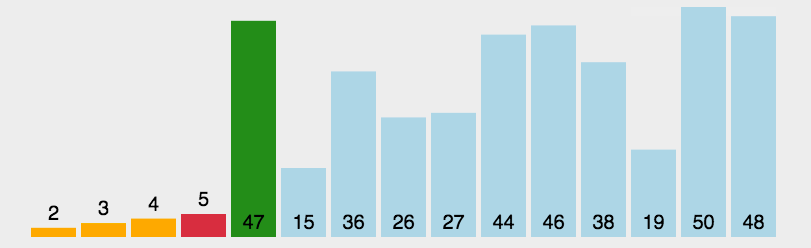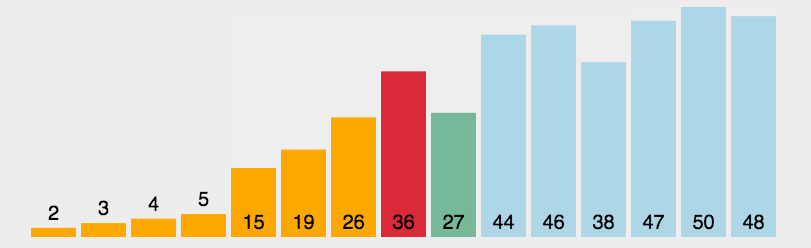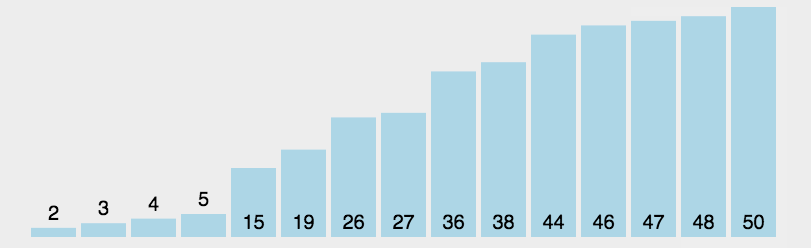
我们还是以 [3, 44, 38, 5, 47, 15, 36, 26, 27, 2, 46, 4, 19, 50, 48] 为例,初始如下图所示:

初始状态下,所有元素都是待排序元素,在其中找到最小的元素(也就是2),和待排序序列的第一个元素(也就是3)交换,这样第一个元素就是最小的,也是排好序的,这样剩下的元素就是下次的待排序元素,第2个元素就成了待排序序列的第一个元素,再从这个待排序序列里找最小元素,和这个第2个元素交换,如此重复就能排好整个序列,具体如下图所示:

复杂度
| 平均时间复杂度 | 最好情况 | 最坏情况 | 空间复杂度 |
|---|---|---|---|
| O(n^2) | O(n^2) | O(n^2) | O(1) |
最好的情况下,已经有序,最坏情况交换 n - 1 次,逆序交换 n/2 次,即使原数组已排序完成,它也将花费将近 n²/2 次遍历来确认一遍,所以其复杂度为O(n^2),不过不用花费额外空间,空间复杂度是O(1)。
插入排序(Insertion Sort)
对于未排序数据,在已排序序列中从后向前扫描,找到相应位置并插入
排序过程
- 从第一个元素开始,认为该元素已经是有序序列。
- 取出下一个元素,在已排序的序列中从后向前扫描。
- 如果该元素(已排序)大于新元素,则将该元素移到下一位置。
- 重复步骤3,直到找到已排序的元素小于或等于新元素的位置。
- 将新元素插入到该位置后。
- 重复步骤2~5,直到所有元素都排序完毕。
代码实现
public static void insertionSort(int[] arr) {
if (arr == null || arr.length == 0) {
return;
}
//默认第1个元素是有序的,从第2个开始遍历
for (int i = 1; i < arr.length; i++) {
//取出当前元素temp
int temp = arr[i];
//循环前面已经排好序的元素
for (int j = i; j >= 0; j--) {
//如果temp小于扫描的元素,就将扫描的元素挪至下一个位置
if (j > 0 && arr[j - 1] > temp) {
arr[j] = arr[j - 1];
} else {
//如果不小于扫描的元素,就插入到该元素的下一个
arr[j] = temp;
break;
}
}
}
}
步骤拆解演示
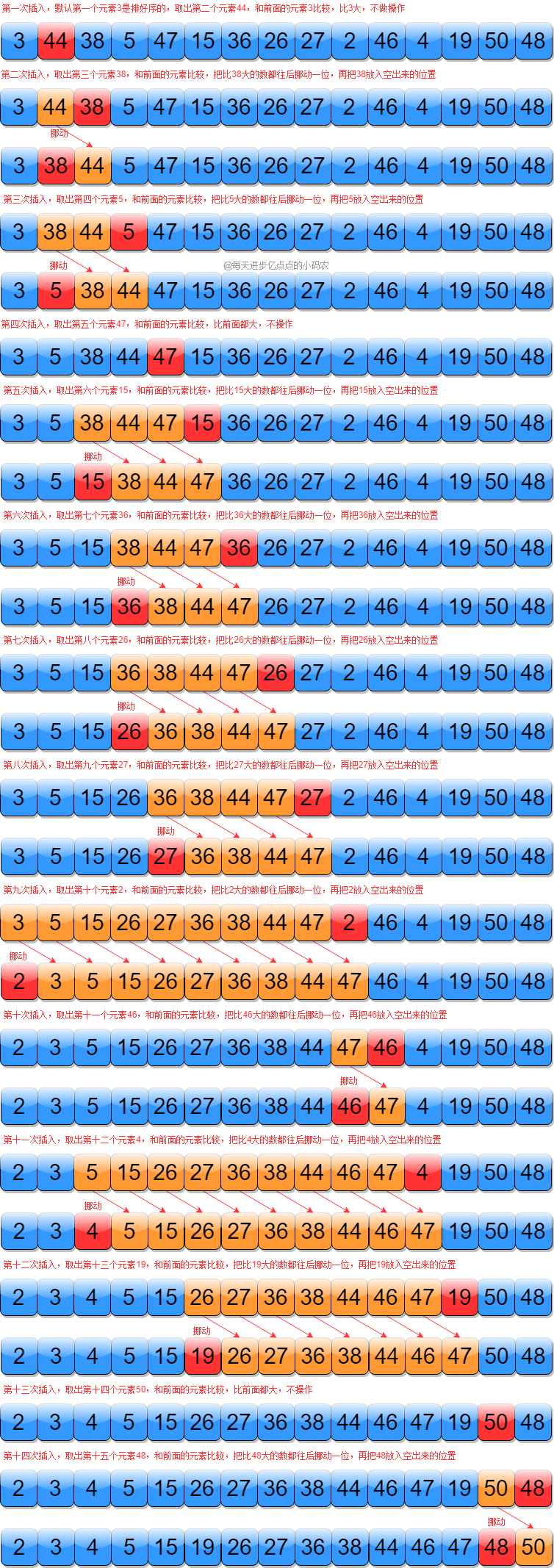
我们还是以 [3, 44, 38, 5, 47, 15, 36, 26, 27, 2, 46, 4, 19, 50, 48] 为例,初始如下图所示:

我们默认第一个元素3是排好的,取第二个元素44和前面的比较,44大于3,不动,然后取第三个元素38和前面的比较,发现38小于44大于3,就把44往后挪,然后把38放置在44的位置上,下面再取第四个元素,重复之前的操作,直到完成排序
复杂度
| 平均时间复杂度 | 最好情况 | 最坏情况 | 空间复杂度 |
|---|---|---|---|
| O(n^2) | O(n) | O(n^2) | O(1) |
最好情况是已经有序,只需当前数跟前一个数比较一下就可以了,这时一共需要比较 n- 1次,复杂度为O(n),最坏情况就是逆序,这时比较次数最多,总次数 = 1+2+…+ (n - 1),所以最坏情况复杂度是O(n2),所以平均复杂度是O(n2),因为不花费额外空间,所以空间复杂度是O(1)。
二分插入排序(Binary Insertion Sort)
我们发现插入排序,在往前扫描找合适插入位置的时候,是逐个扫描的,因为前面是已经排好序的,所以可以使用二分查找的方式提高一点效率,于是就有了二分插入排序(Binary Insertion Sort)
排序过程:
- 从第一个元素开始,认为该元素已经是有序序列。
- 取出下一个元素,在已排序的序列中使用二分查找的方式找到合适的位置索引。
- 将大于该元素的所有元素后移,腾出合适的位置。
- 将新元素插入到该位置。
- 重复步骤2~4,直到所有元素都排序完毕。
代码实现
public static void binaryInsertionSort(int[] arr) {
if (arr == null || arr.length == 0) {
return;
}
for (int i = 1; i < arr.length; ++i) {
int temp = arr[i];
int left = 0, right = i - 1;
// 使用二分查找找到合适的位置索引
while (left <= right) {
int mid = (left + right) / 2;
if (arr[mid] > temp) {
right = mid - 1;
} else {
left = mid + 1;
}
}
// 将大于该元素的所有元素后移,腾出合适的位置
for (int j = i - 1; j >= left; --j) {
arr[j + 1] = arr[j];
}
arr[left] = temp;
}
}
虽然在插入排序的基础上优化了,但是在最坏的情况下,其时间复杂度仍然是 O(n^2),没有使用额外空间,所以空间复杂度是 O(1)
希尔排序(Shell Sort)
将待排序的数组分割成若干个较小的子数组进行插入排序,最后再对整个数组进行一次插入排序
排序过程
- 先选定一个小于数组长度n的整数gap(一般情况下是将n/2作为gap)作为第一增量,然后将所有距离为gap的元素分为一组,并对每一组进行插入排序
- 重复步骤1,每次将gap缩减一半,直到gap等于1停止,这时整个序列被分到了一组,进行一次直接插入排序,排序完成
代码实现
public static void shellSort(int[] arr) {
if (arr == null || arr.length == 0) {
return;
}
//初始间隔设置为数组长度的一半
int gap = arr.length / 2;
while (gap > 0) {
//因为插入排序默认第一个是排好序的,所以每组的第一个元素全部跳过,从第2个元素开始循环,和前面的元素比较
for (int i = gap; i < arr.length; i++) {
//先取出这个元素
int temp = arr[i];
//标记自己组的元素下标
int j = i;
//找自己组的前一个元素,并比较大小,如果比自己大,就把那个元素挪动至自己的位置,并且把下标往前挪,标记前一个同组元素
while (j >= gap && arr[j - gap] > temp) {
arr[j] = arr[j - gap];
j -= gap;
}
arr[j] = temp;
}
//缩小增量
gap /= 2;
}
}
步骤拆解演示
我们还是以 [3, 44, 38, 5, 47, 15, 36, 26, 27, 2, 46, 4, 19, 50, 48] 为例,初始如下图所示:

因为数组长度是15,所以初始增量为 15/2 = 7,然后我们将元素分组,间隔7的元素为1组,3、26、48一组,44、27一组…,如下图所示,相同颜色的为一组:

然后对每组使用插入排序,排序后如下图所示:

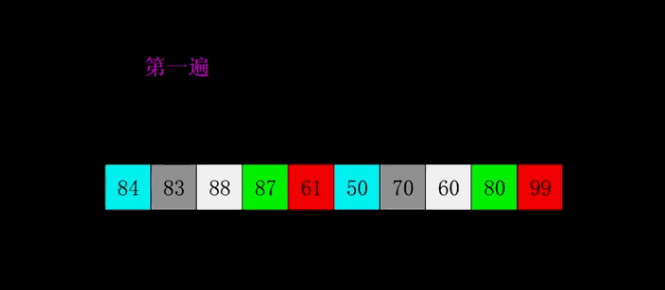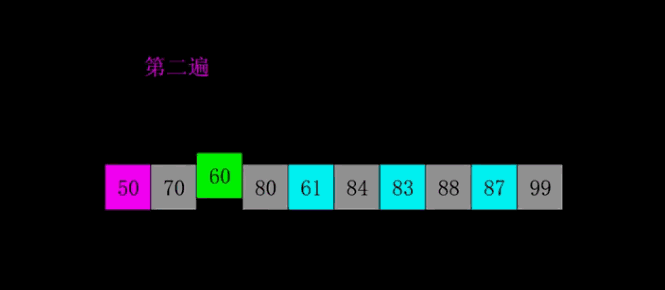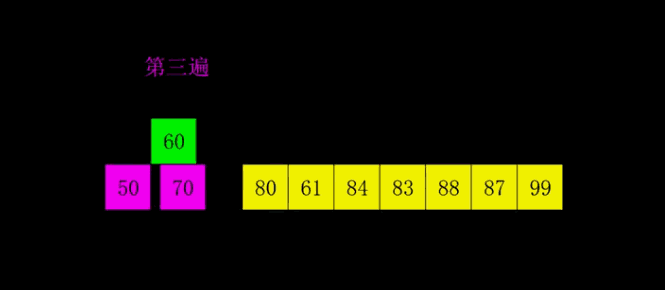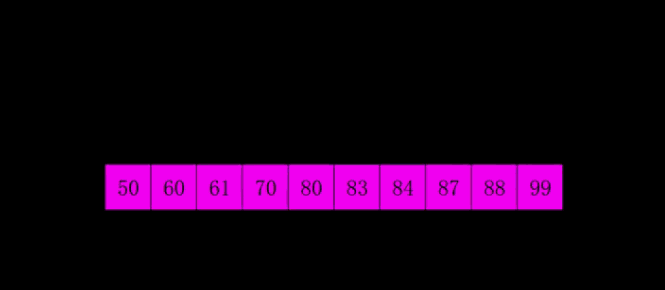
这时候增量需要重新计算,7/2 = 3,然后我们将元素分组,间隔3的元素为1组,3、5、36、38、19一组,27、4、26、46、50一组…,如下图所示,相同颜色的为一组:

然后对每组使用插入排序,排序后如下图所示:

最后,增量再除以2,3/2 = 1,最后所有数是一组,完成一次插入排序,就得到最终排序好的序列

复杂度
| 平均时间复杂度 | 最好情况 | 最坏情况 | 空间复杂度 |
|---|---|---|---|
| O(n log^2 n) | O(n log^2 n) | O(n^2) | O(1) |
希尔排序的时间复杂度不易准确地表示为一个函数,因为它取决于增量序列的选择,总体我们认为是 O(n log n) 到 O(n^2) 之间,不额外花费空间,所以空间复杂度为O(1)。
归并排序(Merging Sort)
通过将待排序的序列逐步划分为更小的子序列,并对这些子序列进行排序,最后再将已排序的子序列合并成一个有序序列

排序过程
- 将待排序的数组递归地分解成若干个小的子数组,直到每个子数组只包含一个元素或为空
- 将相邻的子数组进行合并,得到更大的有序子数组。合并操作从最小的子数组开始,逐步合并直到整个数组排序完成
代码实现
public static void mergingSort(int[] arr) {
if (arr == null || arr.length == 0) {
return;
}
doMergingSort(arr, 0, arr.length - 1);
}
private static void doMergingSort(int[] arr, int left, int right) {
if (left >= right) {
return;
}
int mid = (left + right) / 2;
//递归归并左边
doMergingSort(arr, left, mid);
//递归归并右边
doMergingSort(arr, mid + 1, right);
//开始归并
//创建数组用于放归并后的元素
int[] temp = new int[right - left + 1];
//标记左边数组的起始下标
int lIndex = left;
//标记右边数组的起始下标
int rIndex = mid + 1;
//标记归并后的新数组下标
int index = 0;
// 把较小的数先移到新数组中
while (lIndex <= mid && rIndex <= right) {
//对比两个数组的元素大小,小的就放入新数组,下标++
if (arr[lIndex] < arr[rIndex]) {
temp[index++] = arr[lIndex++];
} else {
temp[index++] = arr[rIndex++];
}
}
//做完上面的操作,最后左边数据或者右边数组还有剩余(只可能一个数组有剩余,不可能两个都剩),移入到新数组里
//把左边数组剩余的数移入数组
while (lIndex <= mid) {
temp[index++] = arr[lIndex++];
}
//把右边剩余的数移入数组
while (rIndex <= right) {
temp[index++] = arr[rIndex++];
}
//将新数组的值赋给原数组
for (int i = 0; i < temp.length; i++) {
arr[i + left] = temp[i];
}
}
步骤拆解演示
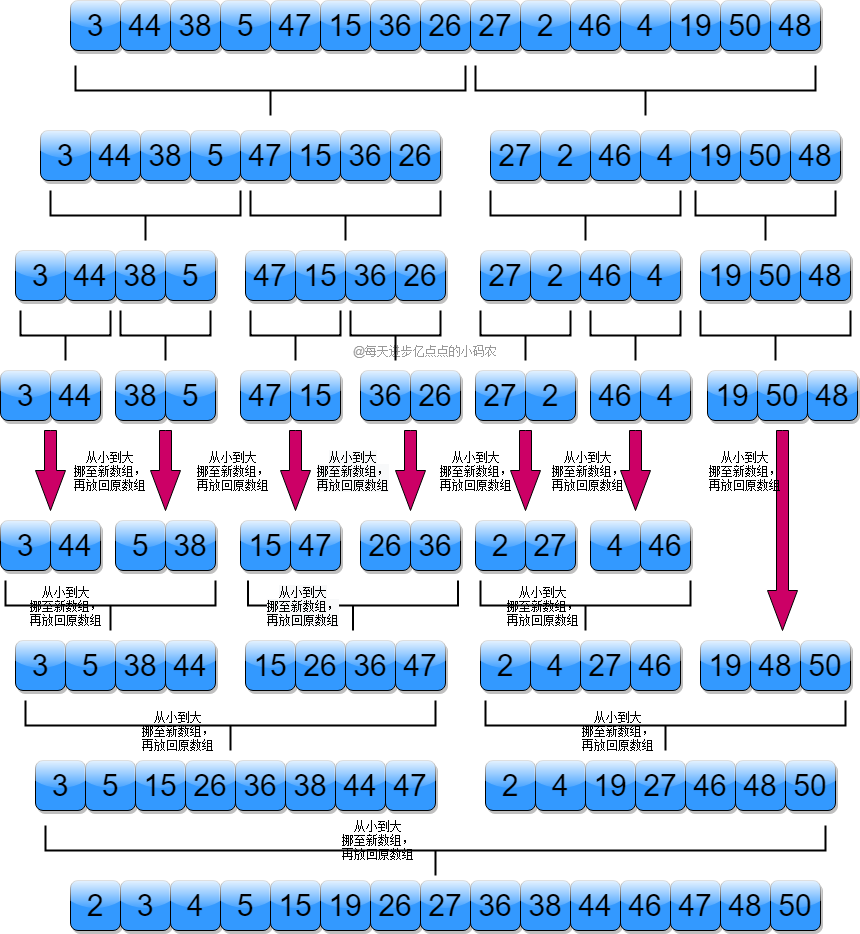
我们还是以 [3, 44, 38, 5, 47, 15, 36, 26, 27, 2, 46, 4, 19, 50, 48] 为例,初始如下图所示:

我们先把数组进行分割,分割成若干个小的子数组,然后再将相邻的子数组合并,如下图所示:
复杂度
| 平均时间复杂度 | 最好情况 | 最坏情况 | 空间复杂度 |
|---|---|---|---|
| O(n log n) | O(n log n) | O(n log n) | O(n) |
分割过程的时间复杂度是O(log n),因为每次都将数组分割成两半。合并过程的时间复杂度是O(n),因为需要将两个有序数组合并成一个有序数组。因此,总的时间复杂度可以表示为O(n log n),其复杂度是稳定的,无论是在最好情况、平均情况还是最坏情况下,都是O(n log n),因为需要创建临时数组来存储合并过程的中间结果,这个临时数组的长度与待排序数组的长度相同,所以空间复杂度是O(n)。
快速排序(Quick Sort)
基于分治思想的排序算法,它通过在数组中选择一个基准元素,将数组分成两个子数组,其中一个子数组的所有元素都小于基准元素,另一个子数组的所有元素都大于基准元素,然后递归地对两个子数组进行排序,最终达到整个序列有序的目的
排序过程
- 从数列中挑出一个元素,称为 “基准”(pivot)
- 重新排序数列,所有元素比基准值小的摆放在基准前面,所有元素比基准值大的摆在基准的后面(相同的数可以到任一边)。在这个分区退出之后,该基准就处于数列的中间位置
- 递归地把小于基准值元素的子数列和大于基准值元素的子数列排序
代码实现
public static void quickSort(int[] arr) {
if (arr == null || arr.length == 0) {
return;
}
doQuickSort(arr, 0, arr.length - 1);
}
public static void doQuickSort(int[] arr, int left, int right) {
if (left >= right) {
return;
}
//分区
int partitionIndex = partition(arr, left, right);
//递归左分区
doQuickSort(arr, left, partitionIndex - 1);
//递归右分区
doQuickSort(arr, partitionIndex + 1, right);
}
//分区
public static int partition(int[] arr, int left, int right) {
//基准值
int pivot = arr[left];
//mark标记初始下标
int mark = left;
//循环基准值之后的所有元素
for (int i = left + 1; i <= right; i++) {
if (arr[i] < pivot) {
//如果有小于基准值的元素,把他挪动至标记的下一位(相当于标记+1,然后交换位置)
mark++;
int temp = arr[mark];
arr[mark] = arr[i];
arr[i] = temp;
}
}
//最后把基准值和标记位的值互换(目的是为了把基准值放置到正确的位置)
arr[left] = arr[mark];
arr[mark] = pivot;
return mark;
}
步骤拆解演示
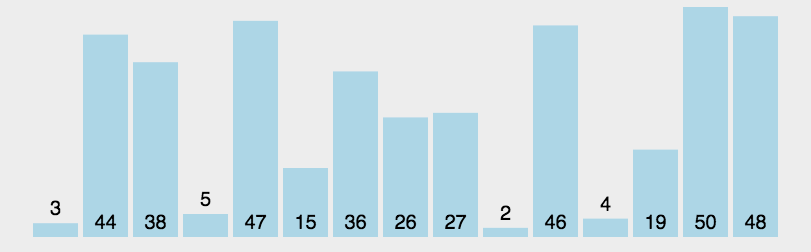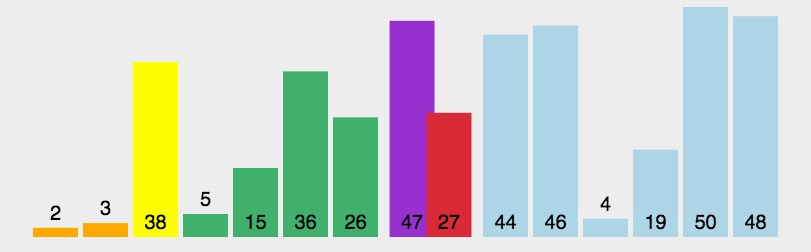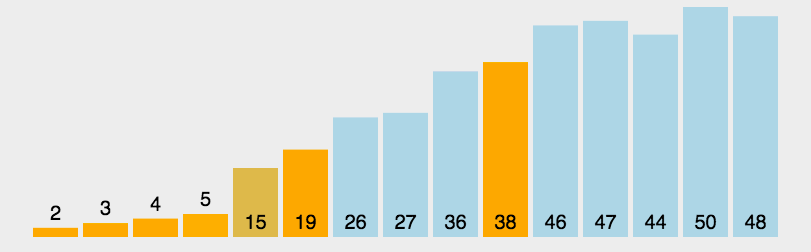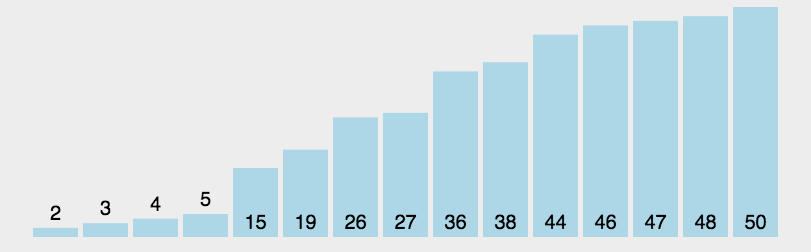
我们还是以 [3, 44, 38, 5, 47, 15, 36, 26, 27, 2, 46, 4, 19, 50, 48] 为例,初始如下图所示:

首先取数组第一个元素为基准值,也就是3,然后把所有小于3的值挪动至3后面(就是和3后面的元素交换),这里只有一个2比3小,所以挪动后,如下图所示:

然后再把基准值3和最后一次调换的元素2交换,如下图所示:

这时候认为3就排好了,然后以3为中心,把数组分割成左右两块,再递归执行上面的操作,因为左侧只有一个元素2,不用操作,对右侧操作即可,右侧数组的第一个元素是38,所以以38为基准值,把小于38的元素挪动到38之后,如下图所示:
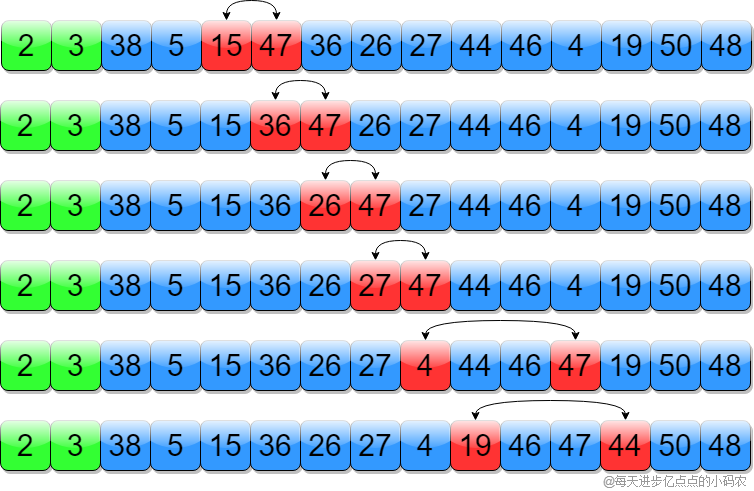
然后再把基准值38和最后一次调换的元素19交换,如下图所示:

这时候38这个元素是排好的了,然后再以38为中心,把数组分割成左右两块,[19, 5, 15, 36, 26, 27, 4] 和 [46, 47, 44, 50 48] ,分别对左右两个数组重复上面的操作,(找基准值,把比基准值小的挪至基准值后面,最后调换基准值和最后一次交换的元素),执行完之后,对左右两个数组分别再分割,直至完成排序

复杂度
| 平均时间复杂度 | 最好情况 | 最坏情况 | 空间复杂度 |
|---|---|---|---|
| O(n log n) | O(n log n) | O(n^2) | O(1) |
最好的情况是,每次划分所选择的中间数恰好将当前序列几乎等分,经过 log n 趟划分,便可得到长度为1的子表。这样,整个算法的时间复杂度为 O(n log n),最坏的情况是,每次所选的中间数是当前序列中的最大或最小元素,这使得每次划分所得的子表中一个为空表,另一子表的长度为原表的长度-1。这样,长度为n的数据表的快速排序需要经过 n 趟划分,使得整个排序算法的时间复杂度为O(n^2)。所以平均复杂度是O(n log n),不额外花费空间,所以空间复杂度是O(1)
堆排序(Heap Sort)
堆排序利用了二叉堆的性质,将待排序的数组构建成一个最大堆(或最小堆),然后将堆顶元素与当前未排序区的最后一个元素交换位置,并对交换后的堆进行调整,直到所有元素都排好序为止

排序过程
- 先将待排序的数组构建成最大堆(或最小堆)
- 将堆顶元素和未排序的最后一个元素交换位置
- 将剩余元素组成的堆调整
- 重复操作2、3步骤直至排序完成
代码实现
public static int[] heapSort(int[] arr) {
if (arr == null || arr.length == 0) {
return;
}
//构建一个最大堆(这边演示正序排序,如果是倒序就构建一个最小堆)
int length = arr.length;
//从最后一个非叶子节点开始向上调整
for (int i = length / 2 - 1; i >= 0; i--) {
adjustHeap(arr, i, length);
}
//上面构建好了最大堆,下面开始排序
//将最大的节点放在堆尾,然后从根节点重新调整
for (int j = arr.length - 1; j > 0; j--) {
//因为最大堆的根节点是最大的,把它和最后一个节点交换,相当于把最大元素排好了
int temp = arr[j];
arr[j] = arr[0];
arr[0] = temp;
//然后再以根节点调整最大堆
adjustHeap(arr, 0, j);
}
return arr;
}
private static void adjustHeap(int[] arr, int i, int length) {
//当前的节点i是父节点,我们先认为它是最大的
int largest = i;
//i节点的左子节点
int left = 2 * i + 1;
//i节点的右子节点
int right = 2 * i + 2;
//比较左子节点和父节点
if (left < length && arr[left] > arr[largest]) {
//如果子节点大于父节点,改标记
largest = left;
}
//比较右子节点和父节点
if (right < length && arr[right] > arr[largest]) {
//如果子节点大于父节点,改标记
largest = right;
}
//如果父节点不是最大值,则交换父节点和最大值,因为调整后可能会导致子树不满足最大堆,所以通过递归调整交换后的子树
if (largest != i) {
//交换
int temp = arr[i];
arr[i] = arr[largest];
arr[largest] = temp;
//调整子树
adjustHeap(arr, largest, length);
}
}
步骤拆解演示
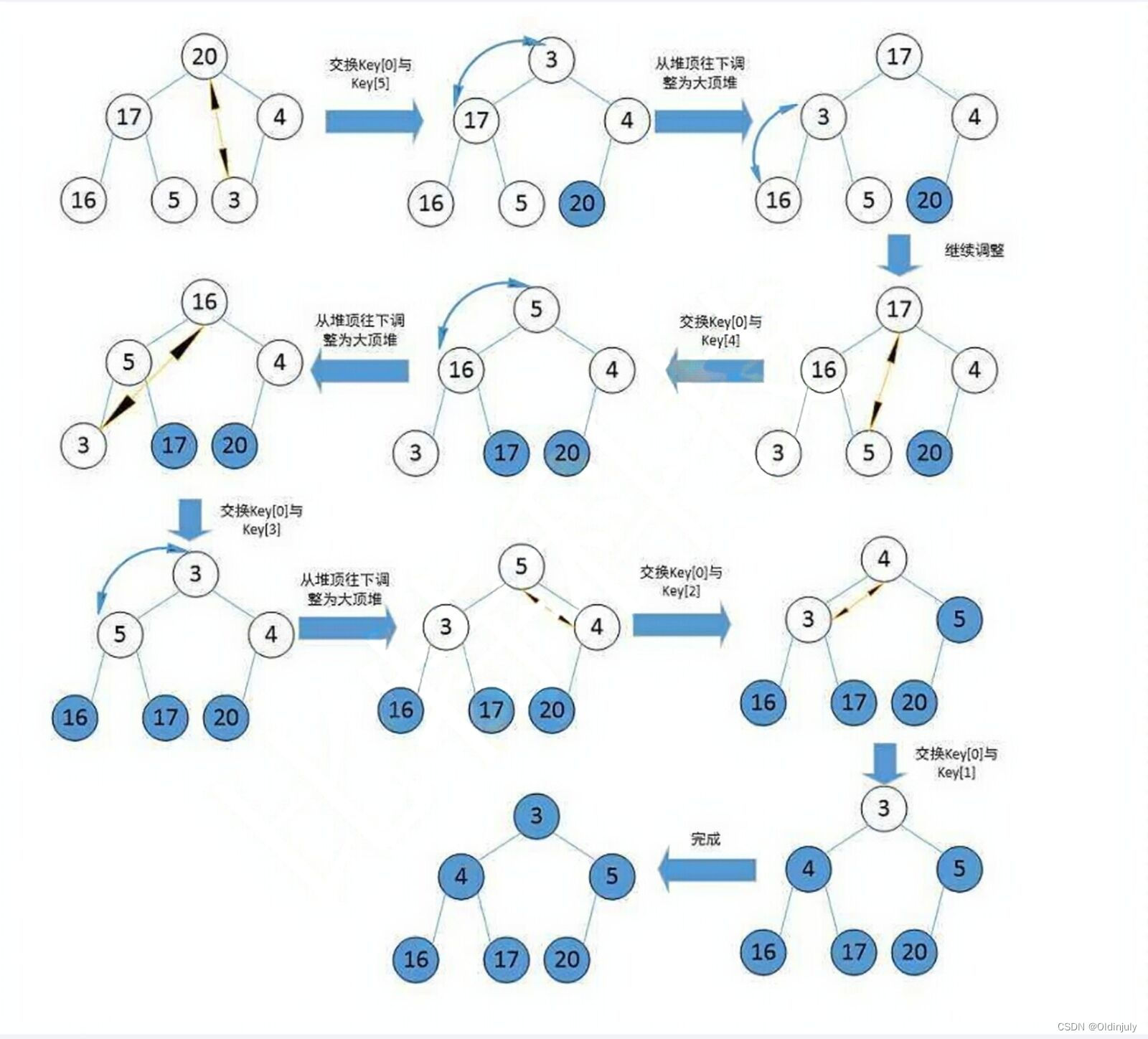
我们还是以 [3, 44, 38, 5, 47, 15, 36, 26, 27, 2, 46, 4, 19, 50, 48] 为例,初始如下图所示:

第一步,我们要把数组构建成一个最大堆(父节点大于等于子节点的特殊完全二叉树),首先可以把这个数组看成是一个完全二叉树,如下图所示:
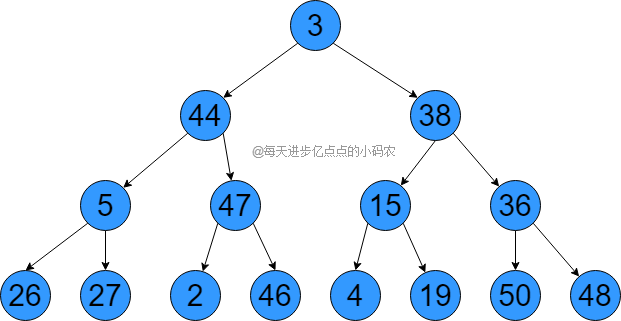
数组的第一个元素(索引为0)将表示树的根节点,对于任意位置 i 的节点,它的左子节点位置为 2 * i + 1,右子节点位置为 2 * i + 2,现在我们需要将这个完全二叉树调整为最大堆,首先找到最后一个非叶子节点(也就是36,位置是数组长度除以2再减1),然后和它的两个子节点比较,找到最大的那个和自己交换,所以就是36和50交换,如下图所示:
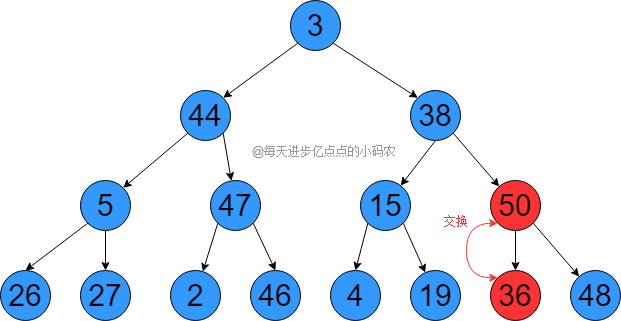
然后按照这个操作,从后往前循环调整前面的所有非叶子节点(15、47、5、38、44、3),调整完15、47、5这三个非叶子节点后,如下图所示:

下面调整38、44的时候,需要注意调整后需要递归调整子树,因为调整后可能会导致子树不满足最大堆,比如38在和50交换之后,38还比子节点48小,还需要和48交换,交换之后,如下图所示:
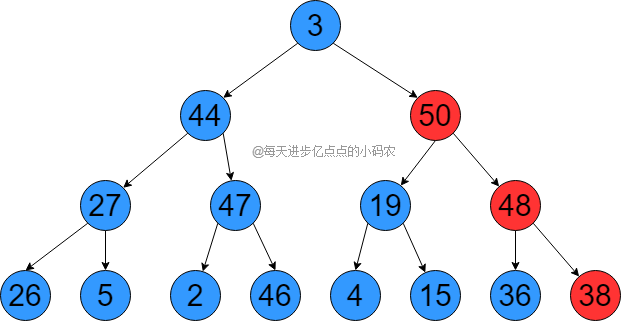
44、3也按这样操作后,就会得到最大堆,如下图所示:
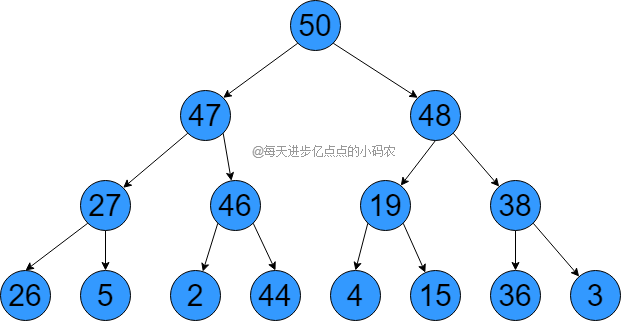
下面就是开始排序,将堆顶元素(最大元素)和未排序的最后一个元素交换位置,也就是50和3交换位置,交换后50在最后一个位置,我们认为他是排好序的(将它从树上挪走,其实它只是在数组的最后一位),如下图所示:
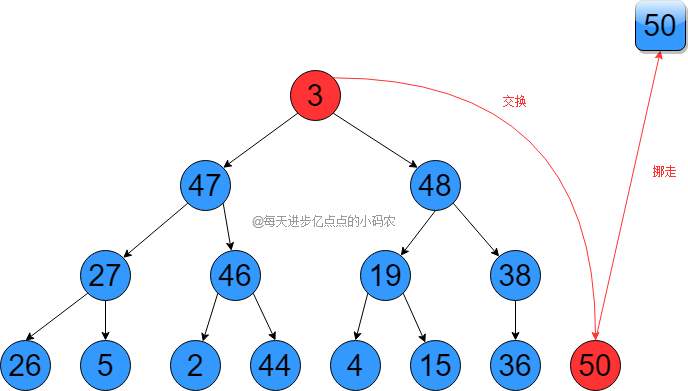
然后剩下的元素,以根节点调整为最大堆(就是拿根节点3和它的子节点47、48比,发现48最大,然后把48和3交换,再比较交换后3的子节点19和38,发现38最大,把38和3交换,再比较交换后3的子节点36,发现36大,再交换36和3),调整后,如下图所示:
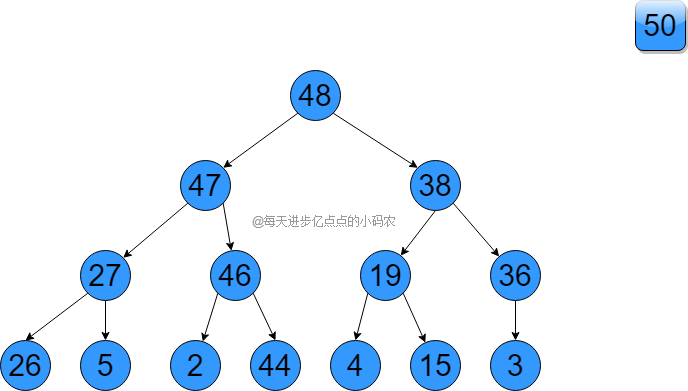
这时候再重复之前的操作,把堆顶和最后的元素交换,48交换3,那么48就排好序了,再调整堆为最大堆,如此重复直到排好序
复杂度
| 平均时间复杂度 | 最好情况 | 最坏情况 | 空间复杂度 |
|---|---|---|---|
| O(n log n) | O(n log n) | O(n log n) | O(1) |
堆排序包括建堆和排序两个操作,建堆过程的时间复杂度是 O(n),排序过程的时间复杂度是 O(n log n),所以,堆排序整体的时间复杂度是 O(n log n),因为没有占用额外空间,所以空间复杂度是O(1)。
四、线性时间非比较类排序
基数排序(Radix Sort)
按照低位先排序,然后收集;再按照高位排序,然后再收集;依次类推,直到最高位。需要注意的是,只能排大于等于0的数

排序过程
- 找到数组里最大的数,以及它的位数
- 按照位数从低位到高位,对元素进行排序,放置于桶中,然后再从桶里收集数据
代码实现
public static void radixSort(int[] arr) {
if (arr == null || arr.length == 0) {
return;
}
//找出数组中最大值,
int max = Arrays.stream(arr).max().getAsInt();
//确定最大值的位数
int maxDigits = (int) Math.log10(max) + 1;
//创建10个桶用于分配元素
int[][] buckets = new int[10][arr.length];
//记录每个桶里的元素个数
int[] bucketSizes = new int[10];
//进行maxDigits轮分配和收集
for (int digit = 0; digit < maxDigits; digit++) {
//分配元素到桶中
for (int num : arr) {
int bucketIndex = (num / (int) Math.pow(10, digit)) % 10;
//将元素放到对应的桶内
buckets[bucketIndex][bucketSizes[bucketIndex]] = num;
//对应桶里的元素数量+1
bucketSizes[bucketIndex]++;
}
//收集桶中的元素
int index = 0;
for (int i = 0; i < 10; i++) {
for (int j = 0; j < bucketSizes[i]; j++) {
arr[index] = buckets[i][j];
index++;
}
//清空桶计数器
bucketSizes[i] = 0;
}
}
}
步骤拆解演示
我们还是以 [3, 44, 38, 5, 47, 15, 36, 26, 27, 2, 46, 4, 19, 50, 48] 为例,初始如下图所示:

首先确定最大值以及它的位数,最大值是50,位数是2位,下面创建10个桶,按个位数的数字摆放这些元素到桶里,比如27个位数是7就放到7那个桶里,如下图所示:

然后从低到高收集每个桶里的元素,如下图所示:

再按十位数的数字摆放这些元素到桶里,比如36十位数是3就放到3那个桶里,如下图所示
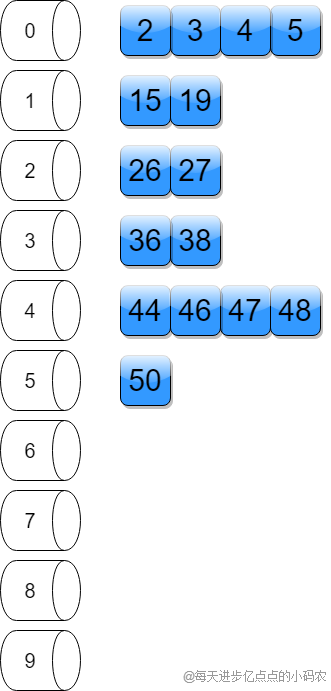
然后从低到高收集每个桶里的元素,就会得到排好序的序列,如下图所示:

复杂度
| 平均时间复杂度 | 最好情况 | 最坏情况 | 空间复杂度 |
|---|---|---|---|
| O(d*(n+r)) | O(d*(n+r)) | O(d*(n+r)) | O(n+r) |
其中,d 为位数,r 为基数,n 为原数组个数。在基数排序中,因为没有比较操作,所以在复杂上,最好的情况与最坏的情况在时间上是一致的。
计数排序(Counting Sort)
将输入的数据值转化为键存储在额外开辟的数组空间中,需要排序的元素必须是整数,并且里面的元素取值要在一定范围内且比较集中
排序过程
- 找出待排序的数组中最大和最小的元素
- 统计数组中每个值为i的元素出现的次数,存入数组count的第i项
- 对所有的计数累加(从count中的第一个元素开始,每一项和前一项相加)
- 反向填充目标数组:将每个元素i放在新数组的第count(i)项,每放一个元素就将count(i)减去1
代码实现
public static int[] countingSort(int[] arr) {
if (arr == null || arr.length <= 1) {
return arr;
}
//找出数组中的最大值、最小值
int max = Integer.MIN_VALUE;
int min = Integer.MAX_VALUE;
for (int num : arr) {
max = Math.max(max, num);
min = Math.min(min, num);
}
//初始化计数数组count,长度为最大值减最小值加1
int[] count = new int[max - min + 1];
for (int num : arr) {
//数组中的元素要减去最小值作为新索引
count[num - min]++;
}
//计数数组变形,新元素的值是前面元素累加之和的值
int sum = 0;
for (int i = 0; i < count.length; i++) {
sum += count[i];
count[i] = sum;
}
//倒序遍历原始数组,从统计数组找到正确位置,输出到结果数组
int[] sortedArr = new int[arr.length];
for (int i = arr.length - 1; i >= 0; i--) {
sortedArr[count[arr[i] - min] - 1] = arr[i];
count[arr[i] - min]--;
}
return sortedArr;
}
步骤拆解演示
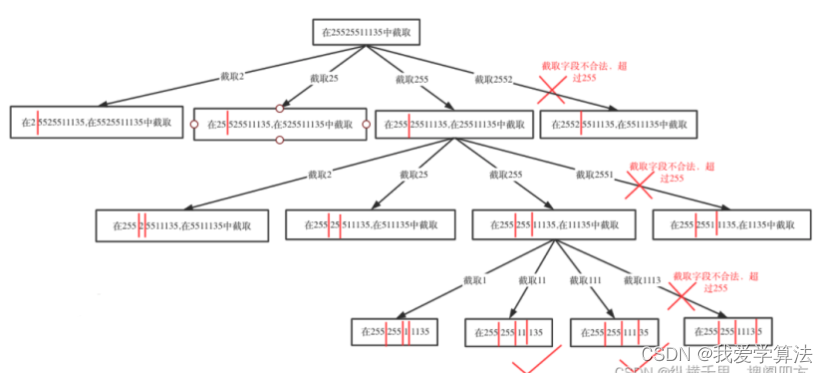
我们还是以 [2, 3, 8, 7, 1, 2, 2, 2, 7, 3, 9, 8, 2, 1, 4, 2, 4, 6, 9, 2] 为例,先找到最大值和最小值,分别为 9 和 1,然后我们建一个 count 数组,长度是 max - min + 1,所以是 9,然后把待排序数组里的值减去最小值就得到 count 数组的下标位置,每有一个,count 加 1,比如元素 7 减去最小值 1 得到 6,就是 7 这个元素在 count 数组里的下标
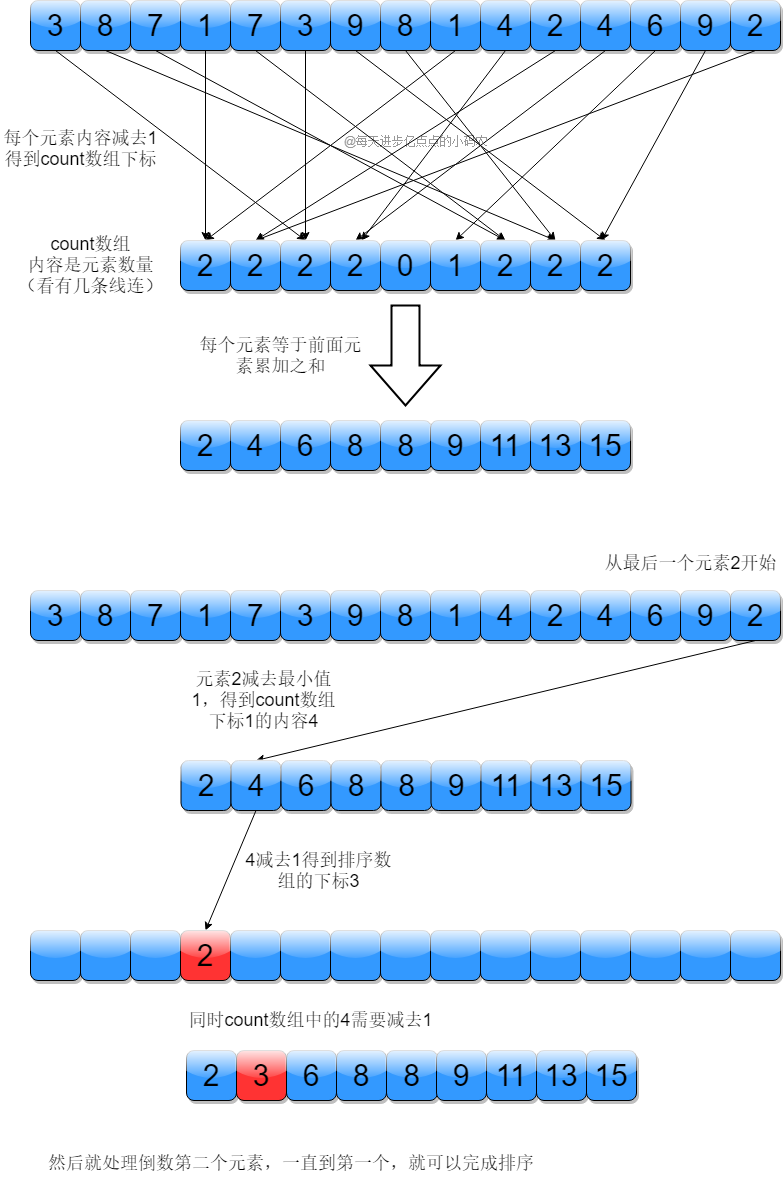
复杂度
| 平均时间复杂度 | 最好情况 | 最坏情况 | 空间复杂度 |
|---|---|---|---|
| O(n + k) | O(n + k) | O(n + k) | O(k) |
n表示的是数组的个数,k表示的 max - min + 1 的大小。
桶排序(Bucket Sort)
将待排序的元素分配到有限数量的桶中,然后对每个桶中的元素进行排序,最后按照桶的顺序将各个桶中的元素依次取出,适用于数据分布范围已知,在分布范围内均匀分布,并且数据量不能过大的场景
排序过程
- 根据待排序序列的最大值和最小值,确定需要的桶的数量
- 遍历待排序序列,根据元素的大小将其分配到对应的桶中
- 对每个桶中的元素进行排序(可以使用其他排序算法,如插入排序、快速排序等)
- 按照桶的顺序,依次将每个桶中排好序的元素取出,就可以得到有序序列
代码实现
public static int[] bucketSort(int[] arr) {
if (arr == null || arr.length <= 1) {
return arr;
}
//找出数组中的最大值、最小值
int max = Integer.MIN_VALUE;
int min = Integer.MAX_VALUE;
for (int value : arr) {
max = Math.max(max, value);
min = Math.min(min, value);
}
//计算桶的数量
int bucketNum = (max - min) / arr.length + 1;
//创建桶
List<List<Integer>> bucketArr = new ArrayList<>(bucketNum);
for (int i = 0; i < bucketNum; i++) {
bucketArr.add(new ArrayList<>());
}
//将每个元素放入桶
for (int value : arr) {
//算出元素应该放的桶
int num = (value - min) / (arr.length);
bucketArr.get(num).add(value);
}
//对每个桶进行排序(可以使用其他排序算法,如插入排序、快速排序等),这里用的Collections.sort()
for (List<Integer> bucket : bucketArr) {
Collections.sort(bucket);
}
//将桶中的元素赋值到原序列
int index = 0;
for (List<Integer> bucket : bucketArr) {
for (Integer i : bucket) {
arr[index++] = i;
}
}
return arr;
}
步骤拆解演示
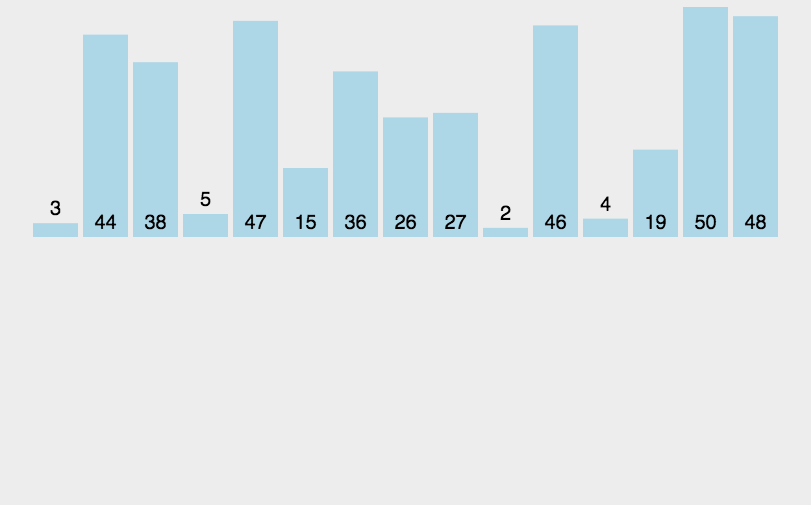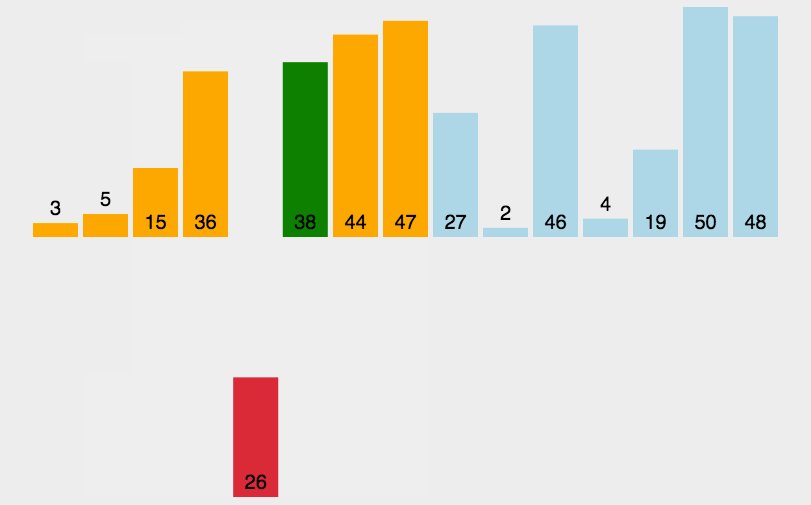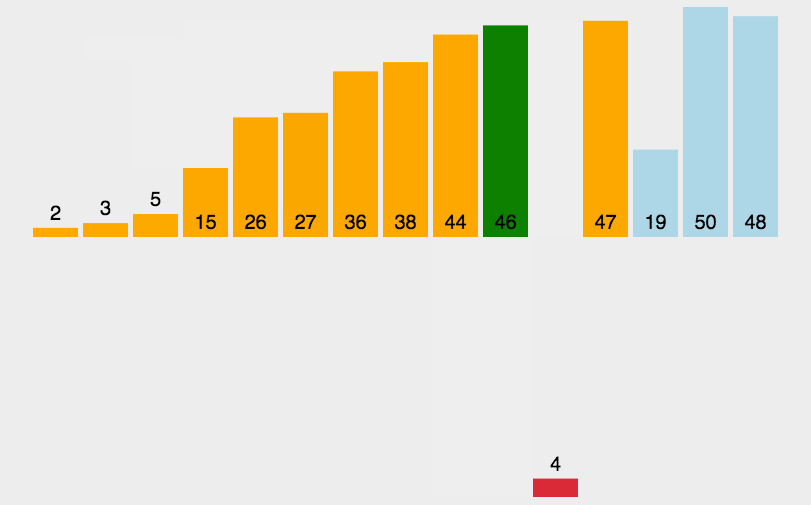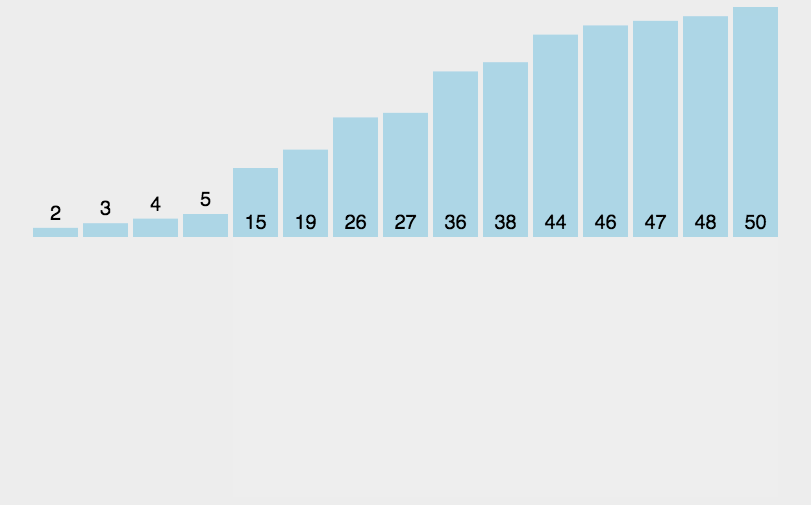
我们还是以 [3, 44, 38, 5, 47, 15, 36, 26, 27, 2, 46, 4, 19, 50, 48] 为例,初始如下图所示:

第一步,根据待排序序列的最大值和最小值,确定需要的桶的数量,计算方式是最大值减最小值,然后除以数组长度,最后再加1,int bucketNum = (max - min) / arr.length + 1;这里最大是50,最小是2,数组长度15,算出来是桶的数量是4,然后根据每个元素的值减去最小值之后,再除以数组长度得到需要放置的桶,int num = (value - min) / (arr.length);,按顺序一个一个放到桶里,就得到下图:

然后针对每个桶内部做排序,排序后,如下图:
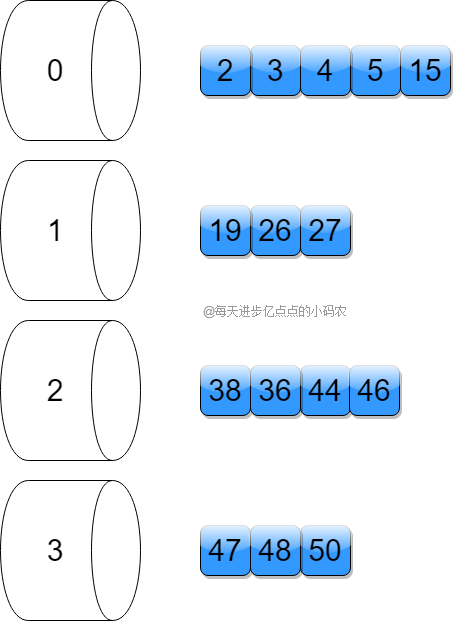
然后再从前往后,把每个桶的元素取出,就可以得到排好序的序列

复杂度
| 平均时间复杂度 | 最好情况 | 最坏情况 | 空间复杂度 |
|---|---|---|---|
| O(n + c) | O(n) | O(n log n) | O(n + m) |
有n个元素进行排序的话,其时间复杂度可以分为两个部分:
- 循环计算每个元素所属桶的映射函数,其时间复杂度是O(n)
- 对每个桶进行排序,比较算法复杂度的最好情况是O(n log n)
所以尽可能均匀分布元素到每个桶里,并且尽可能增加桶的数量,极限情况下,一个桶就一个元素,就可以避免桶内排序,但是这样会导致空间浪费
对于n个元素,m个桶,平均每个桶 n/m 个数据,可以得到复杂度计算公式:
O(n) + O(m * (n/m) * log(n/m))
=O(n + n * (logn - logm))
极限情况下,一个桶就一个元素,也就是 n = m 时,桶排序的复杂度可以达到最好情况的 O(n),平均复杂度为 O(n + c) ,c = n * (logn - logm),最差情况,所有元素在一个桶里,也就是 m = 1,复杂度为 O(n log n) ,如果桶内排序选择较差的插入排序之类的,复杂度会退化到 O(n^2),空间复杂度是待排序元素加上桶数,也就是 O(n + m)。
五、Java中Arrays.sort()用的什么排序算法
原本学了基础的十大排序算法,就结束了,但是我就好奇 Java 里的排序底层用了什么排序算法,于是去看了 Arrays.sort() 的源码,这一看不得了,发现了新大陆。。。
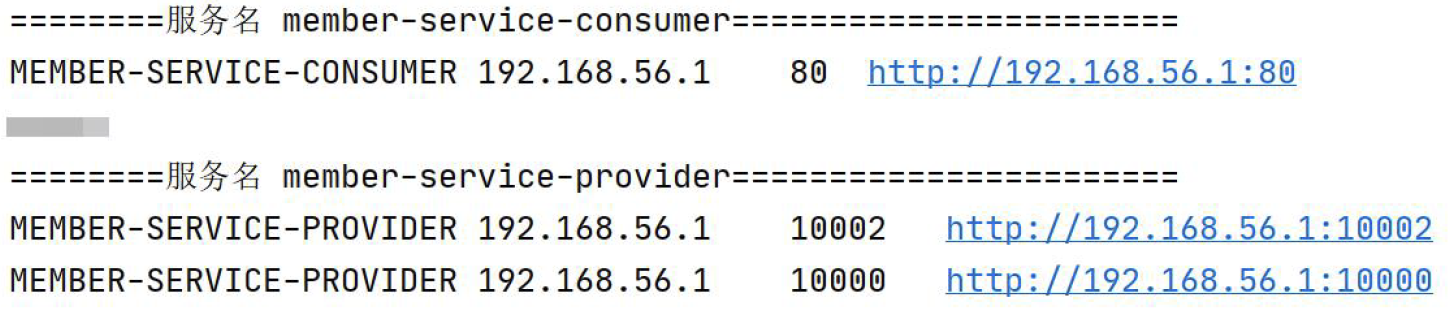
首先,针对基本数据类型和对象类型,使用了不同的算法,如下图
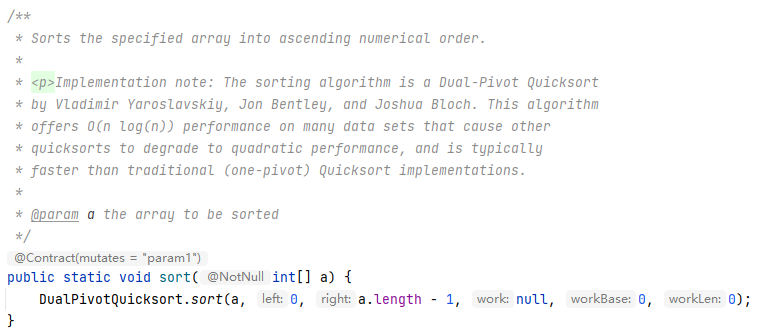
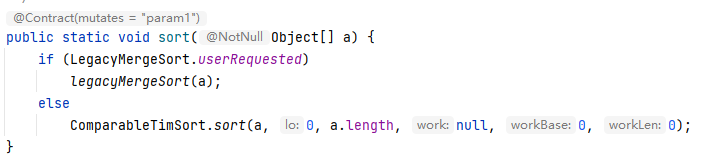
对于基本数据类型,使用了 DualPivotQuicksort,对于对象类型使用了 TimSort(ps:也可以通过配置改成归并排序),我们逐一来看
Dual-Pivot Quick Sort(双轴快速排序)
Dual-Pivot Quick Sort(双轴快速排序)是一种快速排序算法,是传统快速排序的进阶版,Java里的这个 DualPivotQuicksort.sort() 方法内部并不是直接使用双轴快速排序,而是根据不同的数组长度选择不同的排序算法,可以简单总结如下:
- 1 <= len < 47:使用插入排序
- 47 <= len < 286 : 使用快速排序
- 286 < len 且数组有一定顺序:使用归并排序
- 286 < len 且数组无顺序:使用快速排序
流程图
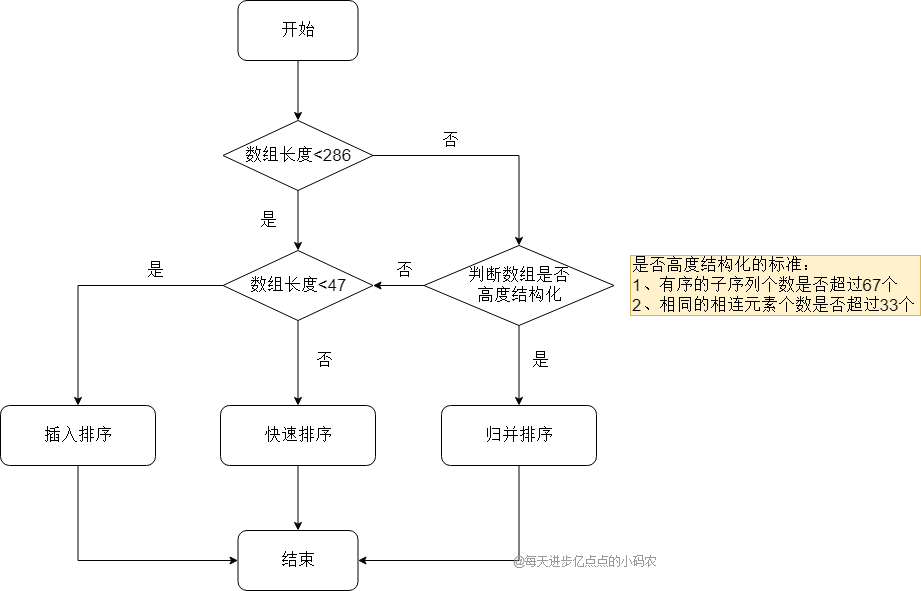
下面重点讲下双轴快排:
我们原本的快速排序其实是单轴快排,会选取一个基准点 pivot,双轴快排其实就是选两个基准点 pivot1和 pivot2,这样可以规避单轴快排时,基准点总是选中最大或者最小的值,而导致复杂度退化到O(n^2),双轴通过两个基准点可以将区间划为三部分,这样不仅每次能够确定2个元素,最坏最坏的情况就是左右同大小并且都是最大或者最小,但这样的概率相比一个最大或者最小还是低很多很多,选取到基准点之后排序方式和单轴快排是一样的,所以重点就在于怎么选取两个基准点 pivot1 和 pivot2,具体步骤如下:
- 通过数组长度 n / 7 算出轴长,然后算出序列的中间数 e3,
- 然后用 e3 往前减1个轴长和2个轴长,得到 e2 和 e1,后面加1个轴长和2个轴长,得到 e4 和 e5,
- 然后使用插入排序将这五个位置的数排序,排序后如果5个数相邻的数两两不相同(
a[e1] != a[e2] && a[e2] != a[e3] && a[e3] != a[e4] && a[e4] != a[e5]),就取 e2 和 e4 位置的两个数为 pivot1 和 pivot2,使用双轴快排,否则就取 e3 位置的数为 pivot 使用单轴快排。
可以看 Java 源码里的注释:

Tim Sort
Tim Sort 是一种混合排序算法,结合了归并排序(Merge Sort)和插入排序(Insertion Sort)的优点。它由Tim Peters于2002年设计,号称世界上最快的排序算法。
下面直接看源码
static void sort(Object[] a, int lo, int hi, Object[] work, int workBase, int workLen) {
assert a != null && lo >= 0 && lo <= hi && hi <= a.length;
//计算数组的长度
int nRemaining = hi - lo;
//如果数组长度小于2,一定有序,直接返回
if (nRemaining < 2)
return;
//如果数组长度小于32,就是用二分插入排序
if (nRemaining < MIN_MERGE) {
//找到数组从起始位置开始的第一个run(连续递增或递减的子数组,递减的翻转)的长度
int initRunLen = countRunAndMakeAscending(a, lo, hi);
//因为第一个run的是已经排序好的,从后面开始使用二分插入排序
binarySort(a, lo, hi, lo + initRunLen);
return;
}
//接下来是主要的排序
ComparableTimSort ts = new ComparableTimSort(a, work, workBase, workLen);
//根据待排序数组长度计算最小run分区大小minRun,介于16-32之间
int minRun = minRunLength(nRemaining);
do {
//计算当前run(连续递增或递减的子数组,递减的翻转)的长度
int runLen = countRunAndMakeAscending(a, lo, hi);
//如果run的长度小于minRun,则会将其扩展到min(minRun, nRemaining) 的长度
if (runLen < minRun) {
//nRemaining代表剩余元素大小,如果nRemaining小于minRun,则将剩余元素处理完毕
int force = nRemaining <= minRun ? nRemaining : minRun;
//使用二分插入排序对指定范围元素排序
binarySort(a, lo, lo + force, lo + runLen);
runLen = force;
}
//将run压入待处理的栈中(其实压入的是起始下标和长度)
ts.pushRun(lo, runLen);
/**
* 不满足以下两个条件,就执行merge操作,直到满足以下两个条件(很有意思,可以看看源码)
* 1. runLen[i - 3] > runLen[i - 2] + runLen[i - 1] 栈顶第3个元素大于栈顶第2个和第1个元素之和
* 2. runLen[i - 2] > runLen[i - 1] 栈顶第2个元素大于栈顶第1个元素
**/
ts.mergeCollapse();
//更新下一个run的起始位置(lo)以及数组中剩余元素(nRemaining),继续寻找下一个run
lo += runLen;
nRemaining -= runLen;
} while (nRemaining != 0);
//最后,使用mergeForceCollapse方法将剩余的所有run进行合并,以完成排序
assert lo == hi;
ts.mergeForceCollapse();
assert ts.stackSize == 1;
}
源码中有几个重点:
run
首先有一个很重要的概念,叫 run,这个 run 是什么呢,可以理解为分区,每一个 run 都是递增或者递减的子数组,比如 [1, 3, 7, 6, 4, 8, 9] 可以拆分成 [1, 3, 7]、[6, 4]、[8, 9]三个 run,而且会把倒序的 run 翻转,以保证所有的 run 都是单向递增的。具体怎么获取 run的长度 以及翻转的,可以看看源码:
/**
* 计算待排序数组中从指定位置开始升序或严格降序的run长度,
* 如果是run是降序,还需进行反转(确保方法返回时run始终是升序的)
*
* run最长升序条件满足(注意有等于号,相等的数认为是满足升序条件):
*
* a[lo] <= a[lo + 1] <= a[lo + 2] <= ...
*
* run最长降序条件满足(注意没有等于号,相等的数认为是不满足降序条件):
*
* a[lo] > a[lo + 1] > a[lo + 2] > ...
*
* 为了保证算法的稳定性,必须严格满足降序条件,以便在进行反转时不破坏稳定性
*
* @param a 待排序的数组
* @param lo 计算run分区的起始索引下标
* @param hi 计算run分区的结束索引下标
* @param c 比较器
* @return 返回待排序数组中从指定位置开始升序或严格降序的run长度
*/
private static <T> int countRunAndMakeAscending(T[] a, int lo, int hi,
Comparator<? super T> c) {
//必须满足lo < hi
assert lo < hi;
int runHi = lo + 1;
if (runHi == hi)
return 1;
// Find end of run, and reverse range if descending
if (c.compare(a[runHi++], a[lo]) < 0) { // Descending
//开头的两个元素如果是降序,就循环找到结束下标
while (runHi < hi && c.compare(a[runHi], a[runHi - 1]) < 0)
runHi++;
//降序需要翻转
reverseRange(a, lo, runHi);
} else { // Ascending
//开头的两个元素如果是升序,就循环找到结束下标
while (runHi < hi && c.compare(a[runHi], a[runHi - 1]) >= 0)
runHi++;
}
//计算长度
return runHi - lo;
}
minRun
其次会根据数组长度计算一个 run 的最小长度,控制在16~32之间,在后面循环每个 run 的时候,如果该 run 长度太短,就用二分插入排序把 run 后面的元素插入到前面的 run 里面,比如我们假设 run 的最小长度是3(实际不会这么小,会在16~32之间), 数组[1, 3, 7, 6, 4, 5, 9] ,先找到第一个 run [1, 3, 7] 满足长度大于等于3,跳过,再找第二个 run [6, 4] 反转成 [4, 6] 长度只有2,小于3,所以就会把后面的5用二分插入法插入到这个 run 中,使其满足条件,变成 [4, 5, 6]
/**
* 如果数组大小为2的N次幂,则返回16(MIN_MERGE / 2)
* 其他情况下,逐位向右位移(即除以2),直到找到16-32间的一个数
* MIN_MERGE/2 <= minRun <= MIN_MERGE (MIN_MERGE默认32)
*/
private static int minRunLength(int n) {
assert n >= 0;
int r = 0; // Becomes 1 if any 1 bits are shifted off
while (n >= MIN_MERGE) { //MIN_MERGE是32
r |= (n & 1);
n >>= 1;
}
return n + r;
}
压栈
每划分一个 run 后,就会把这个 run 压栈,然后检查栈顶三个run是否满足合并规则,满足的话就将相邻的run合并
- 如果栈中
run的数量等于1,直接跳过合并; - 如果栈中
run的数量等于2,只要满足下面的run长度小于等于上面的run长度,就会合并; - 如果栈中
run的数量大于2,比较栈顶3个run的长度,下面的长度小于等于中间和上面的长度之和,就从下面和上面中选出较短长度的和中间的合并
执行合并后,会再次检查栈顶的3个元素,不满足条件会再次合并,直至满足条件
光说好像不好理解,画个图把,先说明下源码压入栈的不是整个 run,而是 run 的初始位置和 run 的长度,这里我们用 run(n) 来表示 run,用 runLen(n) 来表示 run 的长度
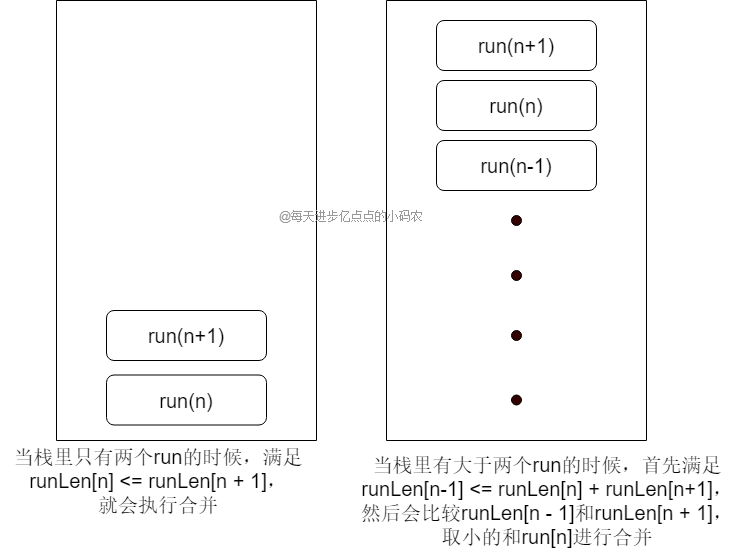
可以参考下源码:
/**
* 检查栈顶三个run是否满足合并规则,满足的话就将相邻的run合并。
* 不满足以下的规则,就会发起合并
*
* 1. runLen[i - 3] > runLen[i - 2] + runLen[i - 1]
* 2. runLen[i - 2] > runLen[i - 1]
*
* 每次有新的run压入栈时就调用这个方法,栈里run的数量必须大于1
*/
private void mergeCollapse() {
//循环条件,栈内run的数量必须大于1
while (stackSize > 1) {
int n = stackSize - 2;
//stackSize > 2 并且栈顶第三个run个长度小于等于栈顶两个run的长度之和
if (n > 0 && runLen[n-1] <= runLen[n] + runLen[n+1]) {
//满足上面的条件之后,从栈顶第一个和第三个中选出小的那个,为了下面和第二个合并
if (runLen[n - 1] < runLen[n + 1])
n--;
//合并
mergeAt(n);
//如果前一条件不满足,当栈顶第二个run的长度小于等于栈顶第一个run时也需要合并
} else if (runLen[n] <= runLen[n + 1])
//合并
mergeAt(n);
} else {
//不满足条件退出
break; // Invariant is established
}
}
}
合并
上面讲到满足一些条件就会把两个 run 进行合并,具体怎么合并的呢?
首先查找 run2 的第一个元素在 run1 中的位置。run1 中这个位置之前的元素就可以忽略(因为它们已经就位)。再查找 run1 的最后一个元素在 run2 中的位置。run2 中这个位置之后的元素就可以忽略(因为它们已经就位)。另外,这里的查找使用了加速查找的方式提高效率(内部其实是先用指数搜索确定大致范围,再使用二分查找具体定位)。
然后用 run1 的后半部分和 run2 的前半部分进行合并,合并的时候,是需要开辟额外空间来提高合并效率的,这个开辟的额外空间是多少才能尽可能的节省空间呢,从 run1 的后半部分和 run2 的前半部分中选出较短的长度作为额外空间的大小,去做合并,如下图

然后就是合并了,这个合并也有讲究,我们知道在归并排序算法中合并两个数组其实就是比较每个元素,把较小的放到相应的位置,然后再比较下一个,这种方式有个不好的地方,拿这里的 run1 和 run2 举例,比如 run1 中有连续的好多元素小于 run2 里的某一个元素,归并排序会一直去比较,浪费时间,所以 Tim Sort 就引入了一个 gallop 模式,当 run1 中小于 run2 的元素连续超过一个阈值(minGallop,初始值是MIN_GALLOP,等于7,这个阈值会变化,后面再说)就会进入 gallop 模式,进入 gallop 模式之后,就不是每次拿一个元素了,而是一串元素(找的时候使用了和上面一样的加速查找),进行合并,并且找到的串的长度不能小于阈值(MIN_GALLOP,固定是7),如果小于就会退出 gallop 模式,如果每次 gallop 循环没有退出,就把 minGallop 减1,minGallop 减少会导致退出 gallop 模式之后,更容易再次进入,而退出 gallop 模式之后,又会将 minGallop 加2,minGallop 增加会导致再次进入到 gallop 模式变难,这里其实就是根据实际的情况,去调整阈值,做平衡,因为如果是比较聚集的数组,我们希望通过 gallop 模式处理(减少比对时间),而随机分布的数组,我们更希望使用单个元素比对的方式处理(减少查找时间)
这里我们先看下 mergeAt 的源码:
/**
* 合并栈中下标位置是i和i+1的两个run
*
*/
private void mergeAt(int i) {
assert stackSize >= 2;
assert i >= 0;
//i必须是栈顶的第二个或者第三个
assert i == stackSize - 2 || i == stackSize - 3;
//获取两个run的其实位置和长度
int base1 = runBase[i];
int len1 = runLen[i];
int base2 = runBase[i + 1];
int len2 = runLen[i + 1];
assert len1 > 0 && len2 > 0;
//必须是连续的两个run
assert base1 + len1 == base2;
/*
* Record the length of the combined runs; if i is the 3rd-last
* run now, also slide over the last run (which isn't involved
* in this merge). The current run (i+1) goes away in any case.
*/
//更新合并后的run长度
runLen[i] = len1 + len2;
if (i == stackSize - 3) {
//当i是栈顶第三个run的时候,就意味着栈顶的run不会被合并(合并第二和第三嘛),所以要把栈顶第二个run的起始位置和长度更新成目前第三个run的
runBase[i + 1] = runBase[i + 2];
runLen[i + 1] = runLen[i + 2];
}
//合并会导致run的数量减少1,所以栈的长度减1
stackSize--;
/*
* Find where the first element of run2 goes in run1. Prior elements
* in run1 can be ignored (because they're already in place).
*/
//查找run2的第一个元素在run1中的位置。这个位置之前的元素在run1中可以忽略
int k = gallopRight(a[base2], a, base1, len1, 0, c);
assert k >= 0;
base1 += k;
len1 -= k;
//当run2的第一个元素在run1的最后一个,说明两个run已经有序,直接返回
if (len1 == 0)
return;
/*
* Find where the last element of run1 goes in run2. Subsequent elements
* in run2 can be ignored (because they're already in place).
*/
//查找run1的最后一个元素在run2中的位置。这个位置之后的元素在run2中可以忽略
len2 = gallopLeft(a[base1 + len1 - 1], a, base2, len2, len2 - 1, c);
assert len2 >= 0;
//当run1的最后一个元素在run2的第一个,说明两个run已经有序,直接返回
if (len2 == 0)
return;
// Merge remaining runs, using tmp array with min(len1, len2) elements
//run1和run2忽略部分元素之后,根据剩余的长度对比,分别调用mergeLo或者mergeHi方法完成合并
if (len1 <= len2)
mergeLo(base1, len1, base2, len2);
else
mergeHi(base1, len1, base2, len2);
}
这里我们看下 mergeLo 的源码:
private void mergeLo(int base1, int len1, int base2, int len2) {
assert len1 > 0 && len2 > 0 && base1 + len1 == base2;
// Copy first run into temp array
//下面这一段是创建一个临时数组tmp,并把较小的去除忽略元素的run拷贝过去
T[] a = this.a; // For performance
T[] tmp = ensureCapacity(len1);
int cursor1 = tmpBase; // Indexes into tmp array
int cursor2 = base2; // Indexes int a
int dest = base1; // Indexes int a
System.arraycopy(a, base1, tmp, cursor1, len1);
// Move first element of second run and deal with degenerate cases
//把run2的第一个元素拷贝到原本run1的起始位置
a[dest++] = a[cursor2++];
//上面那步处理之后,如果run2的元素没有了,就直接把临时数组里的run1拷贝回去,直接完成合并,返回
if (--len2 == 0) {
System.arraycopy(tmp, cursor1, a, dest, len1);
return;
}
//如果run1的长度是1,就把run2复制到原本run1的位置,再把run1的那个元素复制到最后,直接完成合并,返回
if (len1 == 1) {
System.arraycopy(a, cursor2, a, dest, len2);
a[dest + len2] = tmp[cursor1]; // Last elt of run 1 to end of merge
return;
}
Comparator<? super T> c = this.c; // Use local variable for performance
int minGallop = this.minGallop; // " " " " "
outer:
while (true) {
//因为归并排序就是比较两个run中元素的大小,谁小谁就赢了,这里分别用count1和count2来记录run1和run2赢的次数
int count1 = 0; // Number of times in a row that first run won
int count2 = 0; // Number of times in a row that second run won
/*
* Do the straightforward thing until (if ever) one run starts
* winning consistently.
*/
//这一段就是当(count1 | count2)小于阈值(可变)就执行单个元素比对合并,当不满足了,就会跳过这段
do {
assert len1 > 1 && len2 > 0;
if (c.compare(a[cursor2], tmp[cursor1]) < 0) {
a[dest++] = a[cursor2++];
count2++;
count1 = 0;
if (--len2 == 0)
break outer;
} else {
a[dest++] = tmp[cursor1++];
count1++;
count2 = 0;
if (--len1 == 1)
break outer;
}
} while ((count1 | count2) < minGallop);
/*
* One run is winning so consistently that galloping may be a
* huge win. So try that, and continue galloping until (if ever)
* neither run appears to be winning consistently anymore.
*/
//这里是当大于阈值(固定7)的情况,就进入gallop模式,取多段合并
do {
assert len1 > 1 && len2 > 0;
//gallopRight内部其实是先用指数搜索确定大致范围,再使用二分查找具体定位
count1 = gallopRight(a[cursor2], tmp, cursor1, len1, 0, c);
if (count1 != 0) {
System.arraycopy(tmp, cursor1, a, dest, count1);
dest += count1;
cursor1 += count1;
len1 -= count1;
if (len1 <= 1) // len1 == 1 || len1 == 0
break outer;
}
a[dest++] = a[cursor2++];
if (--len2 == 0)
break outer;
count2 = gallopLeft(tmp[cursor1], a, cursor2, len2, 0, c);
if (count2 != 0) {
System.arraycopy(a, cursor2, a, dest, count2);
dest += count2;
cursor2 += count2;
len2 -= count2;
if (len2 == 0)
break outer;
}
a[dest++] = tmp[cursor1++];
if (--len1 == 1)
break outer;
minGallop--;
} while (count1 >= MIN_GALLOP | count2 >= MIN_GALLOP);
if (minGallop < 0)
minGallop = 0;
minGallop += 2; // Penalize for leaving gallop mode
} // End of "outer" loop
this.minGallop = minGallop < 1 ? 1 : minGallop; // Write back to field
if (len1 == 1) {
assert len2 > 0;
System.arraycopy(a, cursor2, a, dest, len2);
a[dest + len2] = tmp[cursor1]; // Last elt of run 1 to end of merge
} else if (len1 == 0) {
throw new IllegalArgumentException(
"Comparison method violates its general contract!");
} else {
assert len2 == 0;
assert len1 > 1;
System.arraycopy(tmp, cursor1, a, dest, len1);
}
}
流程总结
最后总结下 Tim Sort 的整体流程
- 数组长度小于2,直接返回,小于32,使用二分插入排序
- 根据数组长度算出
run(连续递增或递减的子数组) 的最小长度minRun - 开始循环获取
run,得到run的长度,如果递减的,将其翻转,如果run的长度小于minRun,就拿其后面的元素使用二分插入补充到这个run中,使其满足minRun长度 - 把这个
run压入到栈中,并判断栈中的run是否满足合并条件,如果满足就合并(合并时,使用了很多提速和节省空间的手段) - 循环完成后,将剩余的所有的
run合并
复杂度
最后附上和快速排序(Quick Sort)以及归并排序(Merging Sort)的复杂度对比:
| 算法名称 | 平均时间复杂度 | 最好情况 | 最坏情况 | 空间复杂度 |
|---|---|---|---|---|
| 快速排序(Quick Sort) | O(n log n) | O(n log n) | O(n^2) | O(1) |
| 归并排序(Merging Sort) | O(n log n) | O(n log n) | O(n log n) | O(n) |
| Tim Sort | O(n log n) | O(n) | O(n log n) | O(n) |
Tim Sort 在处理一些部分排序好的数的时候,需要的比较次数要远小于 n log n,也是远小于相同情况下的归并排序算法需要的比较次数。但是和其他的归并排序算法一样,最坏情况下的时间复杂度是 O(n log n) 。但是在最坏的情况下,Tim Sort 需要的临时存储空间只有 n/2,在最好的情况下,需要的额外空间是常数级别的。所以各个方面都优于需要 O(n) 空间和稳定 O(n log n) 时间的归并算法。