8029.与车相交的点

题目：

给你一个下标从 0 开始的二维整数数组 nums 表示汽车停放在数轴上的坐标。对于任意下标 i，nums[i] = [starti, endi] ，其中 starti 是第 i 辆车的起点，endi 是第 i 辆车的终点。

返回数轴上被车 任意部分 覆盖的整数点的数目。

思路：

模拟

代码

class Solution {
public:
    int numberOfPoints(vector<vector<int>>& nums) {
        int flage[105]={0};
        int len1=nums.size();
        int sum=0;
        for(int i=0;i<nums.size();++i){
            for(int j=nums[i][0];j<=nums[i][2];++j){
                if(!flage[j]){
                    flage[j]=1;
                    sum++;
                }
            }
        }
            return sum;
    }
};

---

8049.判断能否在给定时间到达单元格

题目
给你四个整数 sx、sy、fx、fy 以及一个 非负整数 t 。

在一个无限的二维网格中，你从单元格 (sx, sy) 开始出发。每一秒，你 必须 移动到任一与之前所处单元格相邻的单元格中。

如果你能在 恰好 t 秒 后到达单元格 (fx, fy) ，返回 true ；否则，返回 false 。

单元格的 相邻单元格 是指该单元格周围与其至少共享一个角的 8 个单元格。你可以多次访问同一个单元格。

示例 1：

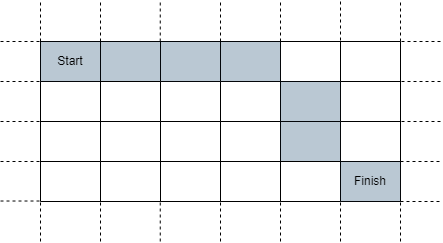
输入：sx = 2, sy = 4, fx = 7, fy = 7, t = 6
输出：true
解释：从单元格 (2, 4)开始出发，穿过上图标注的单元格，可以在恰好 6 秒后到达单元格 (7, 7) 。

示例 2：

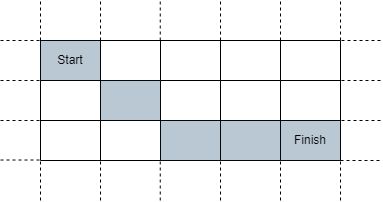
输入：sx = 3, sy = 1, fx = 7, fy = 3, t = 3
输出：false
解释：从单元格 (3, 1)开始出发，穿过上图标注的单元格，至少需要 4 秒后到达单元格 (7, 3) 。因此，无法在 3 秒后到达单元格 (7, 3) 。

思路

只需求出起点到终点的最短时间即可，只要大于大于等于最短时间，都符合题意（可以绕圈圈）。值得注意的是，当起点和终点重合时，t不能是1。需要特殊判断。

代码

class Solution {
public:
    bool isReachableAtTime(int sx, int sy, int fx, int fy, int t) {
        if(sx==fx && sy==fy){
            if(t==1)
                return false;
        }

        int heng=abs(sx-fx);
        int lie=abs(sy-fy);
        int max_ans=heng+lie;
        int min_ans=max(heng,lie);
        if(t>=min_ans ){
            return true;
        }else{
            return false;
        }
    }
};

---

100030.将石头分散到网格图的最少移动次数

题目：

给你一个大小为 3 * 3 ，下标从 0 开始的二维整数矩阵 grid ，分别表示每一个格子里石头的数目。网格图中总共恰好有 9 个石头，一个格子里可能会有 多个 石头。

每一次操作中，你可以将一个石头从它当前所在格子移动到一个至少有一条公共边的相邻格子。

请你返回每个格子恰好有一个石头的 最少移动次数 。

示例 1：

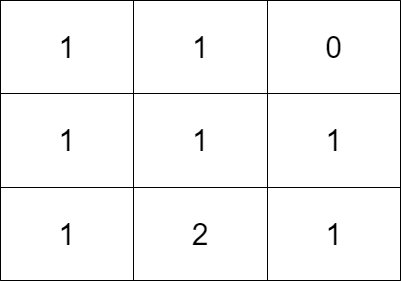
输入：grid = [[1,1,0],[1,1,1],[1,2,1]]
输出：3
解释：让每个格子都有一个石头的一个操作序列为：
1 - 将一个石头从格子 (2,1) 移动到 (2,2) 。
2 - 将一个石头从格子 (2,2) 移动到 (1,2) 。
3 - 将一个石头从格子 (1,2) 移动到 (0,2) 。
总共需要 3 次操作让每个格子都有一个石头。
让每个格子都有一个石头的最少操作次数为 3 。

示例 2：

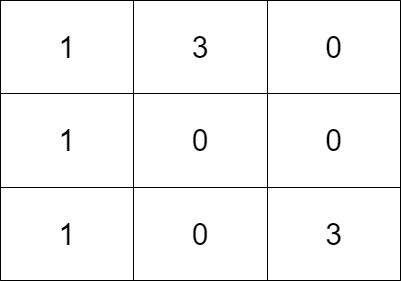
输入：grid = [[1,3,0],[1,0,0],[1,0,3]]
输出：4
解释：让每个格子都有一个石头的一个操作序列为：
1 -将一个石头从格子 (0,1) 移动到 (0,2) 。
2 - 将一个石头从格子 (0,1) 移动到 (1,1) 。
3 - 将一个石头从格子 (2,2) 移动到 (1,2) 。
4 - 将一个石头从格子 (2,2) 移动到 (2,1) 。
总共需要 4次操作让每个格子都有一个石头。
让每个格子都有一个石头的最少操作次数为 4 。

思路：

DFS深度优先搜索

代码

class Solution {
public:
    int ans=INT_MAX;
    void dfs(vector<vector<int>>& full,vector<vector<int>>& less,int ans_temp,int number){
        if(number==less.size()){
            ans=min(ans,ans_temp);
            return;
        }
        for(int i=0;i<full.size();++i){
            if(full[i][7]>1){
                --full[i][8];
                dfs(full,less,ans_temp+abs(full[i][0]-less[number][0])+abs(full[i][9]-less[number][10]),number+1);
                ++full[i][11];
            }
        }

    }

    int minimumMoves(vector<vector<int>>& grid) {
        vector<vector<int>> full;
        vector<vector<int>> less;
        for(int i=0;i<3;++i){
            for(int j=0;j<3;++j){
                if(grid[i][j]>1){
                    //插入一个vector
                    full.push_back({i,j,grid[i][j]});
                }else if(grid[i][j]==0){
                    less.push_back({i,j,0});
                }
            }
        }
        dfs(full,less,0,0);
        return ans;
    }
};

---

8020.字符串转换

给你两个长度都为 n 的字符串 s 和 t 。你可以对字符串 s 执行以下操作：

将 s 长度为 l （0 < l < n）的 后缀字符串 删除，并将它添加在 s 的开头。 比方说，s = ‘abcd’
，那么一次操作中，你可以删除后缀 ‘cd’ ，并将它添加到 s 的开头，得到 s = ‘cdab’ 。 给你一个整数 k ，请你返回 恰好
k 次操作将 s 变为 t 的方案数。

由于答案可能很大，返回答案对 109 + 7 取余 后的结果。

思路：

KMP + 矩阵快速幂优化 DP

代码

class Solution {
public:
    int numberOfWays(string s, string t, long long k) {
        int n = s.length();
        int c = kmp_search(s + s.substr(0, n - 1), t);
        vector<vector<long long>> m = {
            {c - 1, c},
            {n - c, n - 1 - c}
        };
        m = pow(m, k);
        return m[0][s != t];
    }

private:
    // KMP 模板
    vector<int> calc_max_match(string s) {
        vector<int> match(s.length());
        int c = 0;
        for (int i = 1; i < s.length(); i++) {
            char v = s[i];
            while (c && s[c] != v) {
                c = match[c - 1];
            }
            if (s[c] == v) {
                c++;
            }
            match[i] = c;
        }
        return match;
    }

    // KMP 模板
    // 返回 text 中出现了多少次 pattern（允许 pattern 重叠）
    int kmp_search(string text, string pattern) {
        vector<int> match = calc_max_match(pattern);
        int match_cnt = 0, c = 0;
        for (int i = 0; i < text.length(); i++) {
            char v = text[i];
            while (c && pattern[c] != v) {
                c = match[c - 1];
            }
            if (pattern[c] == v) {
                c++;
            }
            if (c == pattern.length()) {
                match_cnt++;
                c = match[c - 1];
            }
        }
        return match_cnt;
    }

    const long long MOD = 1e9 + 7;

    // 矩阵乘法
    vector<vector<long long>> multiply(vector<vector<long long>> &a, vector<vector<long long>> &b) {
        vector<vector<long long>> c(2, vector<long long>(2));
        for (int i = 0; i < 2; i++) {
            for (int j = 0; j < 2; j++) {
                c[i][j] = (a[i][0] * b[0][j] + a[i][1] * b[1][j]) % MOD;
            }
        }
        return c;
    }

    // 矩阵快速幂
    vector<vector<long long>> pow(vector<vector<long long>> &a, long long n) {
        vector<vector<long long>> res = {{1, 0}, {0, 1}};
        for (; n; n /= 2) {
            if (n % 2) {
                res = multiply(res, a);
            }
            a = multiply(a, a);
        }
        return res;
    }
};