一.二叉树链式结构的实现：

1.前置说明：

对于一颗二叉树的构建是比较复杂的在刚刚开始了解二叉树的构建的时候。我们可以通过创建多个节点的方式去构建二叉树的结构，直接连接节点的左右节点构建一个二叉树方便去学习。

1.创建二叉树：

struct TreeNode* byNode(TreeNodeData x)
{
	struct TreeNode* tmp = (struct TreeNode*)malloc(sizeof(struct TreeNode));
	if (tmp == NULL)
	{
		perror(tmp);
		exit(-1);
	}
	tmp->val = x;
	tmp->left = NULL;
	tmp->right = NULL;

	return tmp;
}

void creatTreeNode()
{
	//1.构建二叉树：

	struct TreeNode* n1 = byNode(1);
	struct TreeNode* n2 = byNode(2);
	struct TreeNode* n3 = byNode(3);
	struct TreeNode* n4 = byNode(4);
	struct TreeNode* n5 = byNode(5);
	struct TreeNode* n6 = byNode(6);
	struct TreeNode* n7 = byNode(7);

	n1->left = n2;
	n1->right = n3;
	n2->left = n4;
	n2->right = n5;
	n3->left = n6;
	n3->right = n7;

}
int main()
{
	//1.构建二叉树：
	creatTreeNode();
}

2.二叉树的结构：

1.需要注意的是上面的代码不是创建二叉树的一个正规方法，后面我的博客是会去涉及到二叉树的一个创建：
1.空树：
2.非空树：
从二叉树的概念可知二叉树是递归构建的所以后面的操作都是基于递归构建的内容。

2.二叉树的遍历：

1.二叉树的前中后序遍历：

1.学习二叉树结构，最简单的方式就是遍历。所谓二叉树遍历(Traversal)是按照某种特定的规则，依次对二叉树中的节点进行相应的操作，并且每个节点只操作一次。访问结点所做的操作依赖于具体的应用问题。 遍历是二叉树上最重要的运算之一，也是二叉树上进行其它运算的基础。

2.前中后序遍历递归结构遍历：

1. 前序遍历(Preorder Traversal 亦称先序遍历)——访问根结点的操作发生在遍历其左右子树之前。
2. 中序遍历(Inorder Traversal)——访问根结点的操作发生在遍历其左右子树之中（间）。
3. 后序遍历(Postorder Traversal)——访问根结点的操作发生在遍历其左右子树之后。

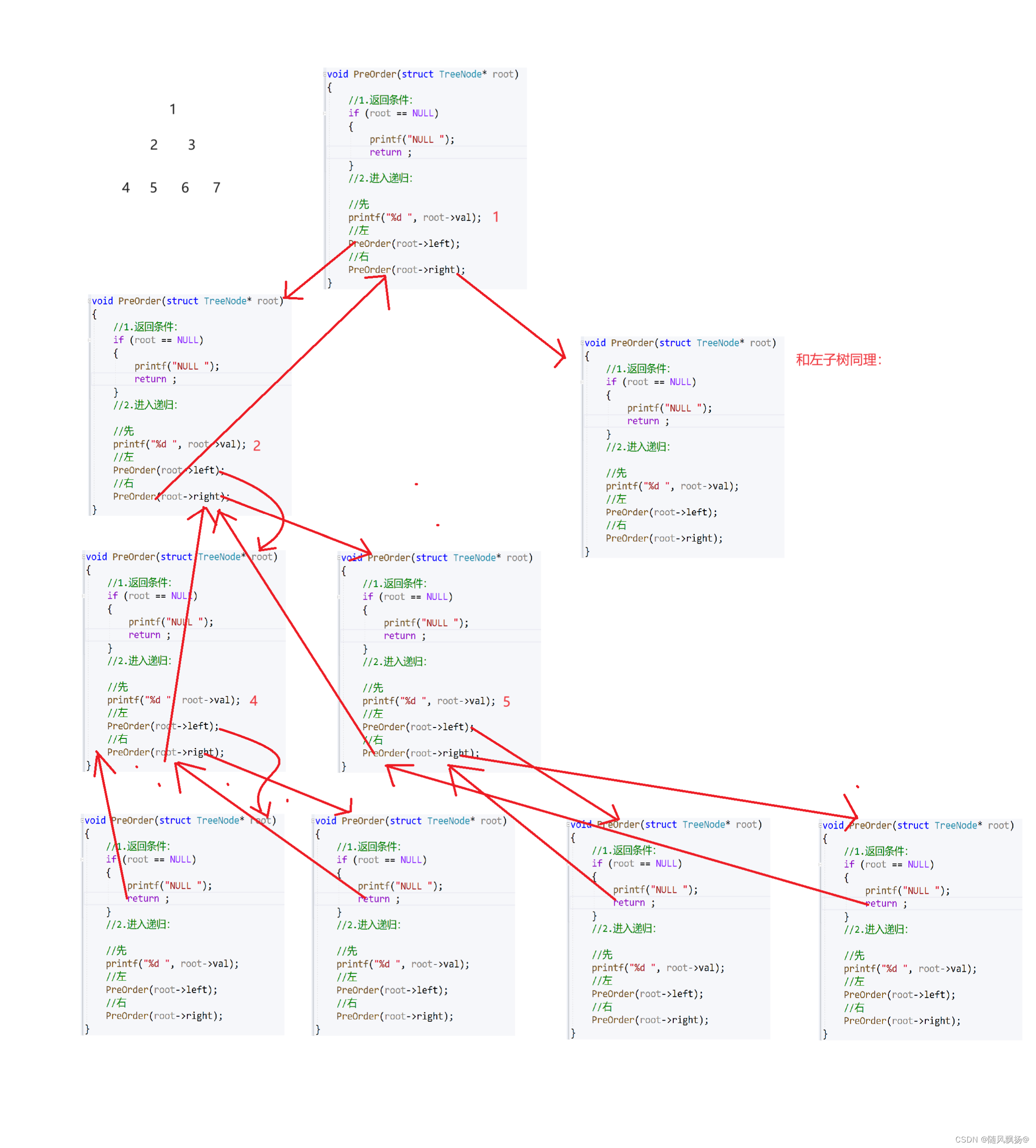
前序遍历：

//1.前序
void PreOrder(struct TreeNode* root)
{
	//1.返回条件：
	if (root == NULL)
	{
		printf("NULL ");
		return ;
	}
	//2.进入递归：

	//先
	printf("%d ", root->val);
	//左
	PreOrder(root->left);
	//右
	PreOrder(root->right);
}

中序遍历：

//2.中序
void InOrder(struct TreeNode* root)
{
	//1.返回条件：
	if (root == NULL)
	{
		printf("NULL ");
		return;
	}
	//2.进入递归：
	//左
	PreOrder(root->left);
	//根：
	printf("%d ", root->val);
	//右
	PreOrder(root->right);
}

后序遍历：

//3.后序
void PostOrder(struct TreeNode* root)
{
	//1.返回条件：
	if (root == NULL)
	{
		printf("NULL ");
		return;
	}
	//2.进入递归：

	//左
	PreOrder(root->left);
	//右
	PreOrder(root->right);
	//根：
	printf("%d ", root->val);
}

2.内容拓展：

一.普通二叉树：
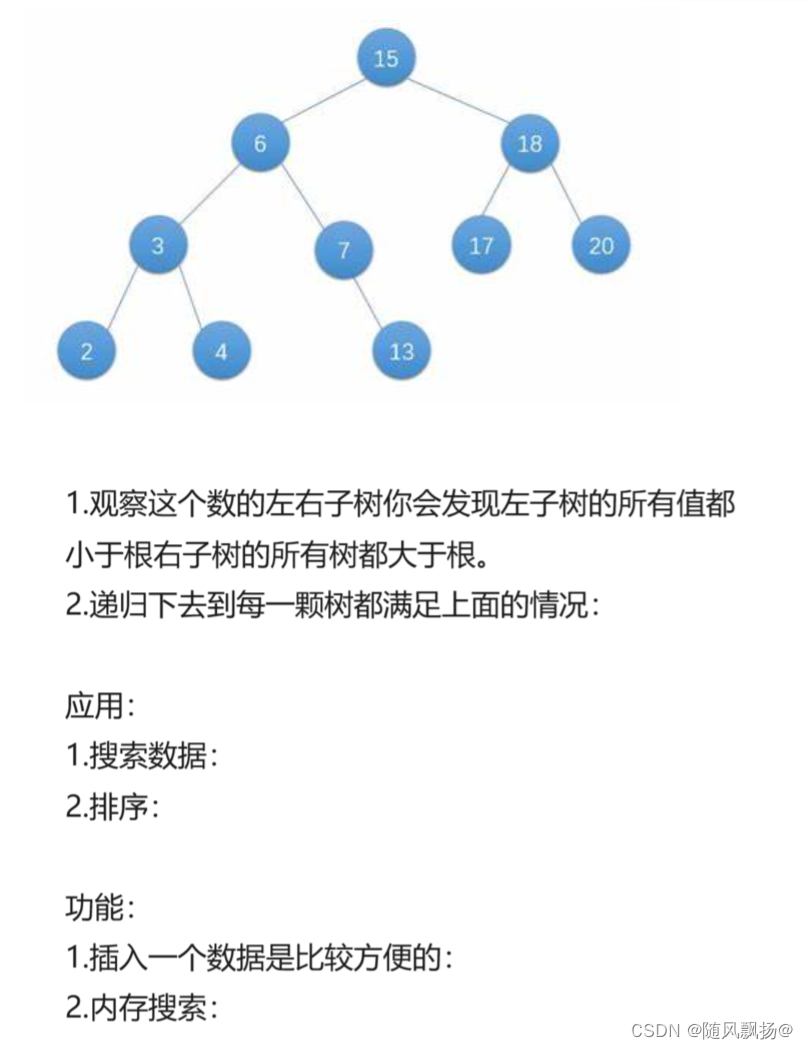
1.增删查改是没有意义的：内容上的增删查改对二叉树的结构造成破坏：

二.二叉搜索树(链式结构)：
1.AVL树：
2.红黑树：
3.二叉树的oj题目：

二.二叉树链式(题目)

题目一：计算节点的个数：

方法一：注意事项：

1.创建在函数里面创建静态局部变量进入递归函数这个变量不会再一次创建：
2.注意root到空的时候的返回值为0：
3.注意不要去创建多个树如果存在多个树去计算节点会导致静态变量数值的问题：

//题目一：计算节点个数：

//方法一(使用局部静态)：
int TreeSize(TN* root)
{
	//1.返回条件：
	if (root == NULL)
	{
		return 0;
	}
	//只会在第一次进入函数去定义：
	static int num = 0;
	//2.进入递归：

	//1.当前节点：
	num++;

	//2.左：
	TreeSize(root->left);
	//3.右：
	TreeSize(root->right);

	return num;
}

方法二：注意事项：

1.使用分治的思路去每次加上一个当前节点的个数。
2.当节点为空的时候就返回一个0.
3.注意：这个函数可以同时去计算多个树的节点个数：

//方法二(使用分治的思路)：
int TreeSize2(TN* root)
{
	if (root == NULL)
		return 0;

	//左节点+右节点
	return TreeSize2(root->left) + TreeSize2(root->right) + 1;
}

题目二：计算叶子节点的个数：

方法一：

1,叶子节点是没有左子树没有右子树的就是叶子节点：
2.遍历每一个节点，并且判断节点是否是叶子节点：
3.使用分治的思路去计数：

int TreeLeafSize(TN* root)
{
	//1.只有叶子才返回：
	if (root->left == NULL && root->right==NULL)
	{
		return 1;
	}

	//2.进入左右子树递归：
	return TreeLeafSize(root->left) + TreeLeafSize(root->right);
}

题目三：求第K层节点的个数：

方法一：

1.函数需要传参数K
2.找根节点的K层就相当于找根节点左子树根的第K-1层：
3.找根节点的K层就相当于找根节点右子树根的第K-1层：
4.进入函数不要多次的进行–，k–不要写在函数中：下一次进入右树的时候就不需要再一次的–了！

//题目三：计算第K层节点个数：

//方法一：

int TreeKSize(TN* root, int k)
{
	assert(k!=0);

	//1.如果在k层没有到的情况下到空返回0
	if (root == NULL)
	{
		return 0;
	}
	//2.当到达K层的时候。
	if (k == 1)
	{
		return 1;
	}

	//3.没有到达K层并且没有为空的时候就进入递归：
	//3-1:进入不同的栈中只要是同层的就可以保证K值相同：
	k--;
	return TreeKSize(root->left, k)+TreeKSize(root->right,k);
}

题目四：

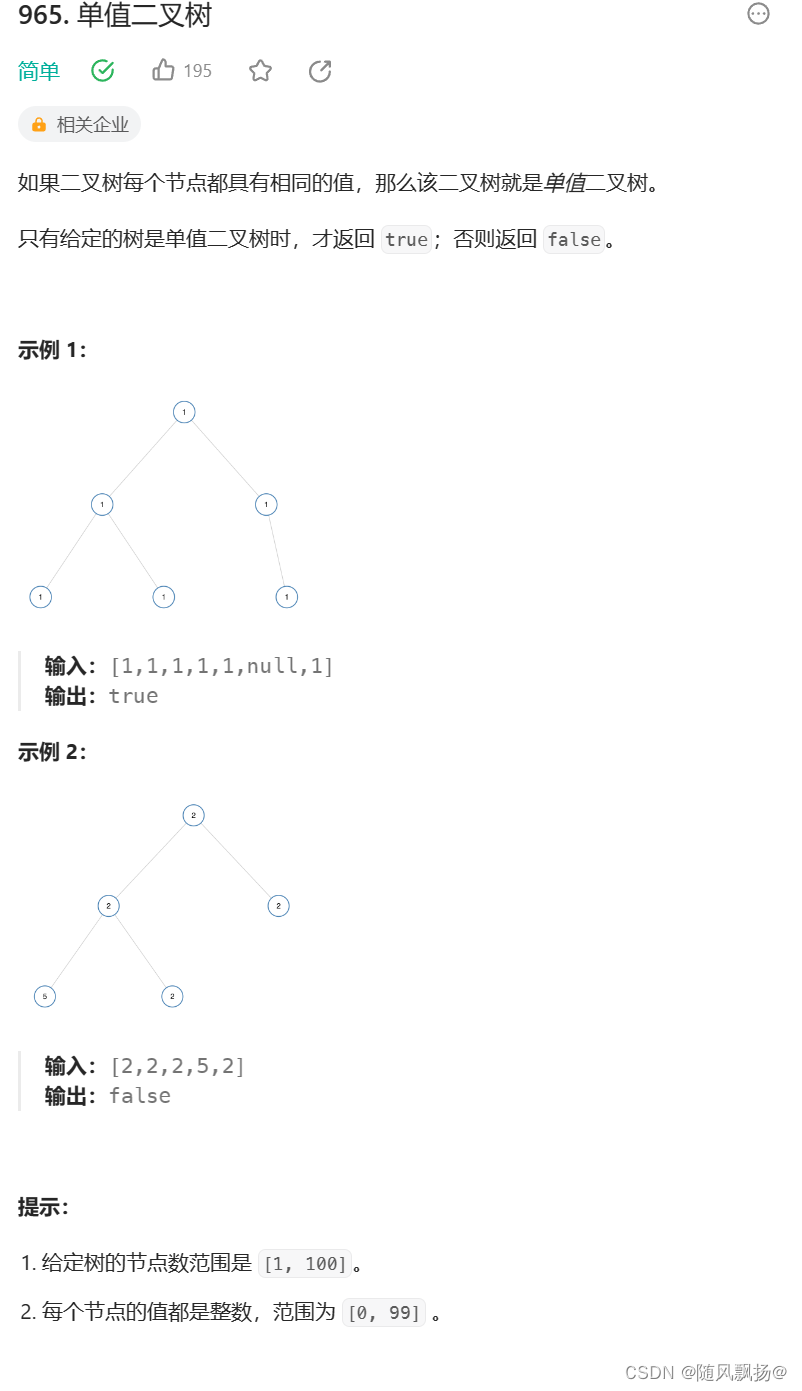
题目链接：单值二叉树

方法一：重新定义一个函数：

1.我们前面大部分的操作就是root为空就返回(true)(因为我们是比较数值是否相同所有返回true):
2…如果每一次通过root的数值去判断我们是需要传数值到递归的下一个部分：
3.如果左子树有不相等的就直接返回false(就不需要进入右子树判断)：
4.如果左右相等的就继续函数不需要返回(继续进入函数)。

bool isUnivalTreeNode(struct TreeNode* root,int val)
{
    //1.到空树：
    if(root==NULL)
    {
        return true;
    }
    //2.数值相同：
    if(root->val==val)
    {

    }
    else if(root->val!=val)
    {
        return false;
    }
      //左子树：
    if(isUnivalTreeNode(root->left,root->val))
    {
        //右子树：
        return isUnivalTreeNode(root->right,root->val);
    }
    
    return false;
}

bool isUnivalTree(struct TreeNode* root){
    
    //左子树：
    if(isUnivalTreeNode(root->left,root->val))
    {
        //右子树：
        return isUnivalTreeNode(root->right,root->val);
    }
    
    return false;
}

方法二：(判断左右节点数值和root数值)

1.如果根为空就返回真：
2.如果左右子树的根节点数值和当前root的数值相同就继续递归进入。
3.如果左右子树中有一个节点数值和root的数值不相同就返回

bool isUnivalTree(struct TreeNode* root){
    if(root==NULL)
        return true;
    
    //1.这两个思路可以解决一个为空，一个有的情况。
    //2.解决两个都为空的情况。
    //3.解决两个都不是空的情况。
    if(root->left!=NULL && root->left->val != root->val)
    {
        return false;
    }
    if(root->right!=NULL && root->right->val != root->val)
    {
        return false;
    }

    //进入递归：
    return isUnivalTree(root->left) && isUnivalTree(root->right);
}

题目五：二叉树的最大深度：

方法一：

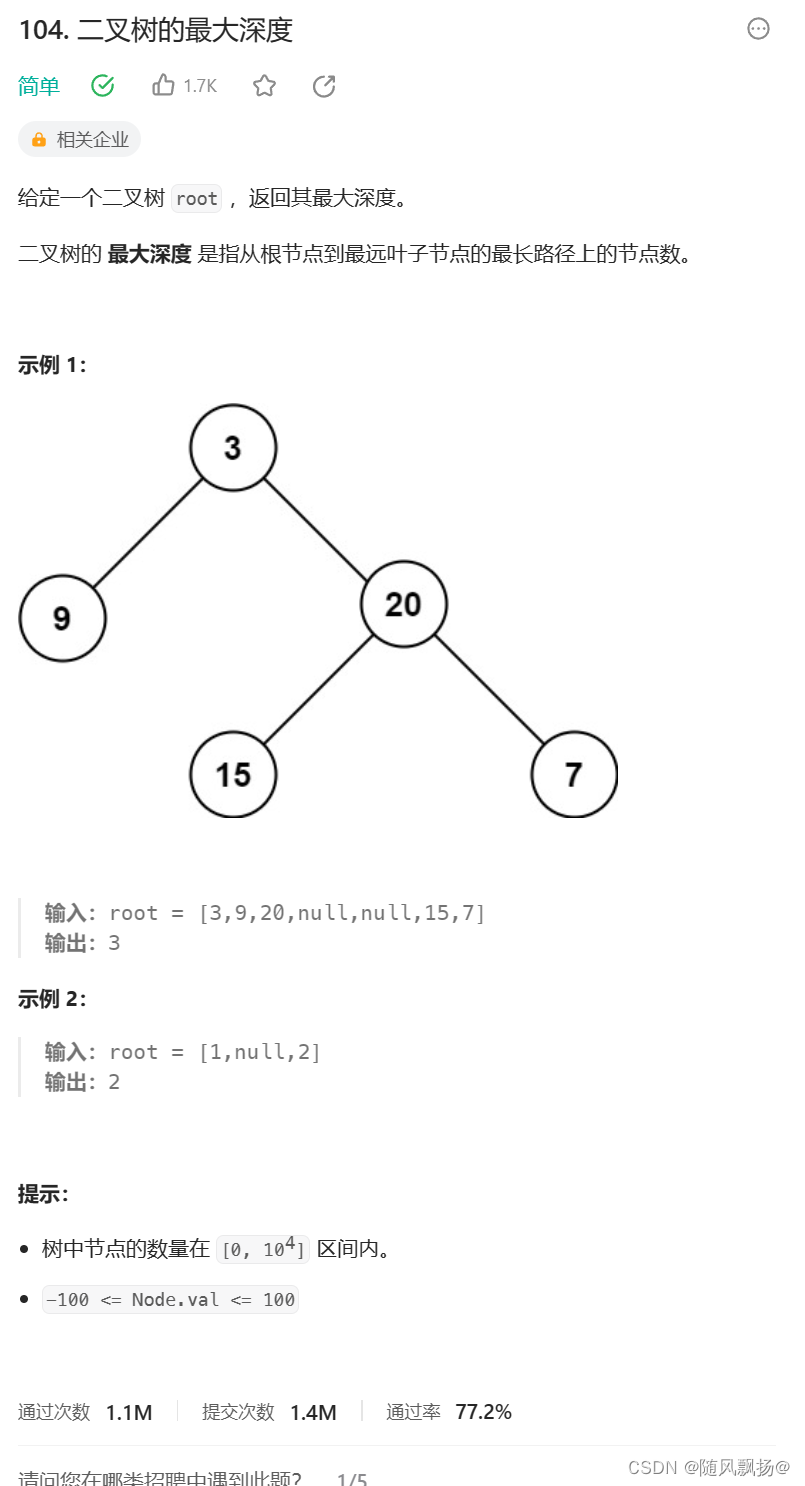
二叉树的深度

1.如果到空就返回0，空不是节点数。
2.每一次比较左右的数的值拿出较大的数值进行+1这个+1就相当加上当前节点。
3.子树的根节点不是空就继续。

int maxDepth(struct TreeNode* root){

    //1.左为空返回0（空节点不是节点数是一个返回的标志）。
    //2.右子树不是空就继续进入函数。
    if(root==NULL)
        return 0;
    
    //2.比较左右子树的返回值取较大的数值：
    int max=maxDepth(root->left);
    int max1=maxDepth(root->right); 

    if(max1>max)
    {
        max=max1;
    }

    //在回去的过程中自己也是节点
    return max+1;
}