物流和供应链管理是当前管理研究的热点和前沿领域。供应链是一个由物流系统和该供应链中的所有单个组织或企业相关活动组成的网络。为满足供应链中顾客需求,需要对商品服务及相关信息,从产地到消费地高效率低成本地流动及储存进行规划、执行和控制。运筹学中对运输模型的研究为达到上述目的提供相应的理论基础。
1 运输问题的数学模型
在经济建设中,经常碰到大宗物资调运问题。如煤、钢铁、木材、粮食等物资,在全国有若干生产基地,根据已有的交通网,应如何制订调运方案,将这些物资运到各消费地点,而总运费要最小。这问题可用以下数学语言描述。
已知有m个生产地点
A
i
,
i
=
1
,
2
,
⋯
,
m
A_i,i=1,2,\cdots ,m
Ai,i=1,2,⋯,m。可供应某种物资,其供应量(产量)分别为
a
i
,
i
=
1
,
2
,
⋯
,
m
a_i,i=1,2,\cdots ,m
ai,i=1,2,⋯,m,有n个销地
B
j
,
j
=
1
,
2
,
⋯
,
n
B_j, j=1,2,\cdots , n
Bj,j=1,2,⋯,n,其需要量分别为
b
j
,
j
=
1
,
2
,
⋯
,
n
b_j,j=1,2,\cdots ,n
bj,j=1,2,⋯,n,从
A
i
A_i
Ai到
B
j
B_j
Bj,运输单位物资的运价(单价)为c,这些数据可汇总于产销平衡表和单位运价表中,见
表4-1,表4-2。有时可把这两表合二为一。
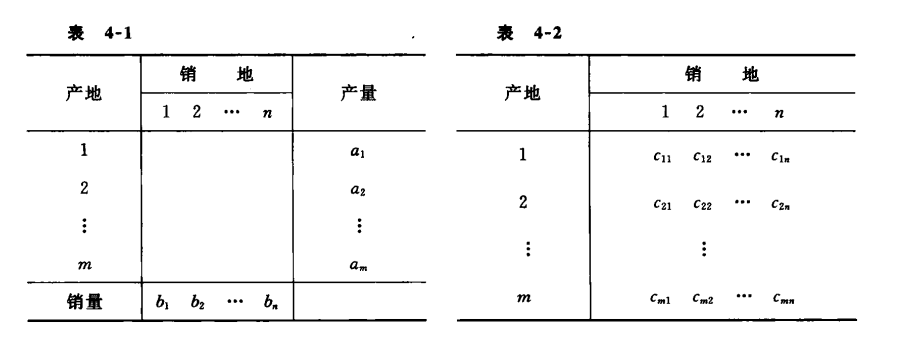
若用
x
i
j
x_{ij}
xij表示从
A
i
A_i
Ai到
B
j
B_j
Bj的运量,那么在产销平衡的条件下,要求得总运费最小的调运方案,可求解以下数学模型
min
z
=
∑
i
=
1
m
∑
j
=
1
n
c
i
j
x
i
j
{
∑
i
=
1
m
x
i
j
=
b
j
,
j
=
1
,
2
,
⋯
,
n
∑
j
=
1
n
x
i
j
=
a
i
,
i
=
1
,
2
,
⋯
,
m
x
i
j
⩾
0
\begin{aligned} \min z=\sum_{i=1}^{m} \sum_{j=1}^{n} c_{i j} x_{i j} \\ \left\{\begin{array}{l} \sum_{i=1}^{m} x_{i j}=b_{j}, \quad j=1,2, \cdots, n \\ \sum_{j=1}^{n} x_{i j}=a_{i}, \quad i=1,2, \cdots, m \\ x_{i j} \geqslant 0 \end{array}\right. \end{aligned}
minz=i=1∑mj=1∑ncijxij⎩
⎨
⎧∑i=1mxij=bj,j=1,2,⋯,n∑j=1nxij=ai,i=1,2,⋯,mxij⩾0
这就是运输问题的数学模型。它包含m*n个变量,(m+n)个约束方程。其系数矩阵的结构比较松散,且特殊。

该系数矩阵中对应于变量x的系数向量P,其分量中除第i个和第m+j个为1以外,其余的都为零。即
P
i
j
=
(
0
⋯
1
⋯
0
⋯
1
⋯
0
)
T
=
e
i
+
e
m
+
j
P_{ij} = (0 \cdots 1 \cdots 0 \cdots 1 \cdots 0)^T = e_i + e_{m+j}
Pij=(0⋯1⋯0⋯1⋯0)T=ei+em+j
对产销平衡的运输问题,由于有以下关系式存在
∑
j
=
1
n
b
j
=
∑
j
=
1
n
(
∑
i
=
1
m
x
i
j
)
=
∑
i
=
1
m
(
∑
j
=
1
n
x
i
j
)
=
∑
i
=
1
m
a
i
\sum_{j=1}^{n} b_{j}=\sum_{j=1}^{n}\left(\sum_{i=1}^{m} x_{i j}\right)=\sum_{i=1}^{m}\left(\sum_{j=1}^{n} x_{i j}\right)=\sum_{i=1}^{m} a_{i}
j=1∑nbj=j=1∑n(i=1∑mxij)=i=1∑m(j=1∑nxij)=i=1∑mai
所以模型最多只有m十n一1个独立约束方程。即系数矩阵的秩≤m十n一1。由于有以
上特征,所以求解运输问题时,可用比较简便的计算方法,习惯上称为表上作业法。
对产销平衡的运输问题,一定存在可行解。又因为所有变量有界,因而存在最优解。
2 表上作业法
表上作业法是单纯形法在求解运输问题时的一种简化方法,其实质是单纯形法,故也
称运输问题单纯形法。但具体计算和术语有所不同。可归纳为:
(1)找出初始基可行解。即在有(m*n)格的产销平衡表上按一定的规则,给出m+n-1个数字,称为数字格。它们就是初始基变量的取值。
(2)求各非基变量的检验数,即在表上计算空格的检验数,判别是否达到最优解。如已是最优解,则停止计算,否则转到下一步。
(3)确定换入变量和换出变量,找出新的基可行解。在表上用闭回路法调整。
(4)重复(2),(3)直到得到最优解为止。
以上运算都可以在表上完成。
2.1 确定初始基可行解
这与一般线性规划问题不同。产销平衡的运输问题总是存在可行解。因有
∑
i
=
1
m
a
i
=
∑
j
=
1
n
b
j
=
d
\sum_{i=1}^m a_i = \sum_{j=1}^n b_j = d
i=1∑mai=j=1∑nbj=d
必存在
x
i
j
≥
0
,
i
=
1
,
⋯
,
m
,
j
=
1
,
…
,
n
x_{ij}≥0, \quad i=1,\cdots,m, \quad j=1,…,n
xij≥0,i=1,⋯,m,j=1,…,n
这就是基可行解。又因
0
≤
x
i
j
≤
m
i
n
(
a
j
,
b
j
)
0 \le x_{ij} \le min(a_j, b_j)
0≤xij≤min(aj,bj)
故运输问题必定存在最优解。
2.1.1 最小元素法
这方法的基本思想是就近供应,即从单位运价表中最小的运价开始确定供销关系,然后次小。一直到给出初始基可行解为止。
2.1.2 伏格尔法
最小元素法的缺点是:可能开始时节省一处的费用,但随后在其他处要多花几倍的运费。伏格尔法考虑到,一产地的产品假如不能按最小运费就近供应,就考虑次小运费,这就有一个差额(也称罚数)。差额越大,说明不能按最小运费调运时,运费增加越多。因而对差额最大处,就应当采用最小运费调运。基于此,伏格尔法的步骤是:
① 首先计算运输表中每一行和每一列的次小单位运价和最小单位运价之间的差值,分别称为行罚数和列罚数。
② 选取这些罚数中最大者(若存在最大罚数相同的情况,则任选其中一个)所在的行或列的最小单位运价所在的格子,在格子中给其分配尽可能大的运量,划去该行 / 该列。
③ 在尚未划去的各行或各列中,重复以上步骤,直到最后一个格子也被分配上运量,得到所求运输问题的初始基可行解。
案例
某部门有 3 个生产同类型的工厂(产地),生产的产品有 4 个销售点(销地)出售,各工厂的生产量(单位:吨)、各销售点的销售量(单位吨)以及各工厂到各销售点单位运价(百元:吨)如下表所示:

适当安排调运方案,最小总运费为()
A . 450
B . 455
C . 460
D . 465
解题过程
- 找出各行各列最小元素和次小元素的差额,最大差值为 B2 列,该列销售量 28 赋予最小元素 5
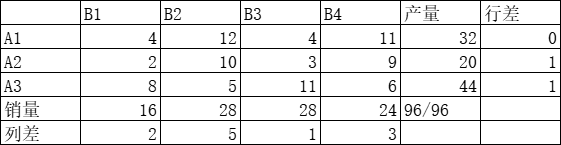
第一次计算运费为 5 ∗ 28 5*28 5∗28
-
重新计算各行各列最小元素和次小元素的差额,最大差值为 B4 列,该列销量 24,由于受产量限制,将 A3 产量 16 赋予最小元素 6
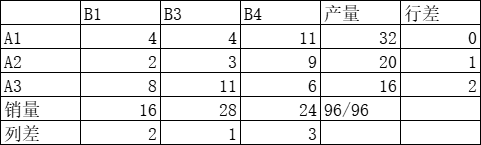
第二次计算的运费为: 5 ∗ 28 + 16 ∗ 6 5*28+16*6 5∗28+16∗6
- 重新计算各行各列最小元素和次小元素的差额。最大差值 B1 列。将销量 16 赋予最小元素 2
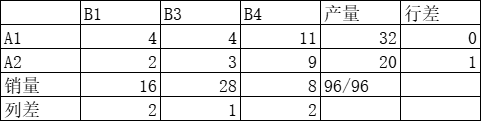
第三次计算: 5 ∗ 28 + 16 ∗ 6 + 2 ∗ 16 5*28+16*6+2*16 5∗28+16∗6+2∗16
-
重新计算各行各列最小元素和次小元素的差额,最大差值 A1 行,赋予销量 28 给元素 4
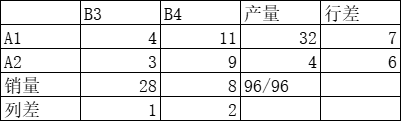
第四次计算: 5 ∗ 28 + 16 ∗ 6 + 2 ∗ 16 + 28 ∗ 4 5*28+16*6+2*16+28*4 5∗28+16∗6+2∗16+28∗4
-
重新计算各行各列最小元素和次小元素的差额,将最后剩下的销量 8 吨中,4 吨分给元素 9,4 吨分元素 11

最终总运费为= 5 ∗ 28 + 16 ∗ 6 + 2 ∗ 16 + 28 ∗ 4 + 11 ∗ 4 + 9 ∗ 4 = 460 5*28+16*6+2*16+28*4+11*4+9*4=460 5∗28+16∗6+2∗16+28∗4+11∗4+9∗4=460
2.2 最优解的判别
2.2.1 闭回路法
2.2.2 位势法
在得到运输问题的初始基可行解后,应对该解做最优性判别。位势法就是用来判断解的最优性的一种方法,其实质是在求解单纯形表中非基变量的检验数。该方法适用于产地和销地较少的运输问题。
★求解步骤
① 在所求得的初始基可行解的表中增加位势列和位势行;
② 由于基变量的检验数等于 0,对这组基变量可以构建位势方程组:




2.3 代码实现
2.3.1 伏格尔法
使用下面的 EXCEL 文件作为运输表(最后一行表示销量,最后一列表示产量),文件名为 TP_PPT_Sample1.xlsx:
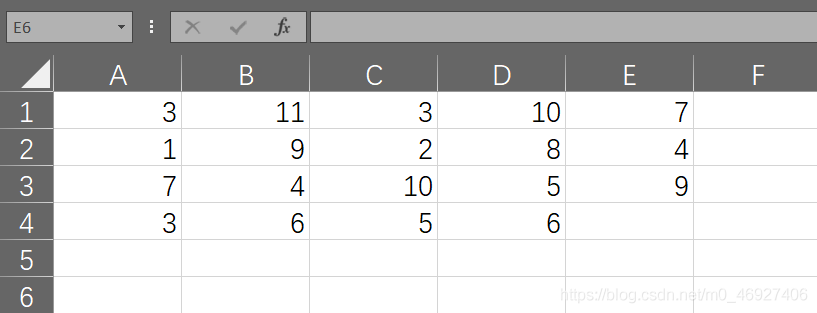
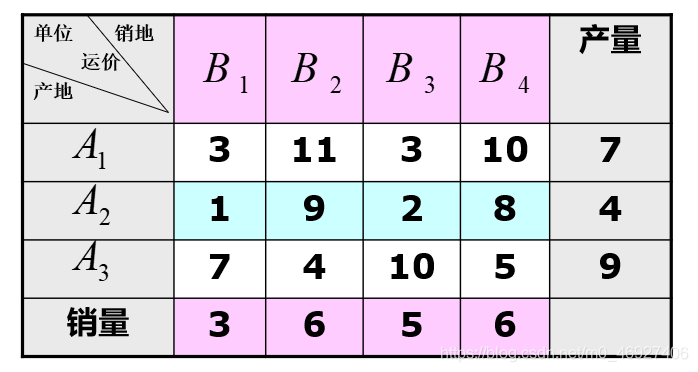
然后在 Python 中执行以下代码:
import numpy as np
import copy
import pandas as pd
# 运输问题求解:使用Vogel逼近法寻找初始基本可行解
def TP_split_matrix(mat):
# 将运输表拆分为成本矩阵c、供给向量a、需求向量b
c = mat[:-1, :-1]
a = mat[:-1, -1]
b = mat[-1, :-1]
return (c, a, b)
def TP_vogel(var):
# Vogel法代码,变量var可以是以numpy.ndarray保存的运输表,或以tuple或list保存的(成本矩阵,供给向量,需求向量)
import numpy
# 检查var的类型
typevar1 = type(var) == numpy.ndarray
typevar2 = type(var) == tuple
typevar3 = type(var) == list
# 格式化输入
if typevar1 == False and typevar2 == False and typevar3 == False:
# 如果var的类型不符合要求,则输出错误信息并返回None
print('>>>非法变量<<<')
(cost, x) = (None, None)
else:
if typevar1 == True:
# 如果var是ndarray类型,则将其拆分为成本矩阵c、供给向量a、需求向量b
[c, a, b] = TP_split_matrix(var)
elif typevar2 == True or typevar3 == True:
# 如果var是tuple或list类型,则直接取出成本矩阵c、供给向量a、需求向量b
[c, a, b] = var
# 深拷贝成本矩阵c,用于记录原始成本矩阵
cost = copy.deepcopy(c)
# 初始化运输方案矩阵x,全为0
x = np.zeros(c.shape)
# 设置一个大的数M,用于表示无穷大
M = pow(10, 9)
# 迭代处理成本矩阵c中的每个元素
for factor in c.reshape(1, -1)[0]:
# 直到所有元素都达到最大值M,或者成本矩阵中所有元素都相等且等于最大值M。
while int(factor) != M:
if np.all(c == M):
break
else:
# 在每次迭代时,将打印当前的成本矩阵c,以便观察迭代过程。
print('c:\n', c)
# 获取行/列最小值数组
row_mini1 = []
row_mini2 = []
for row in range(c.shape[0]):
Row = list(c[row, :])
row_min = min(Row) # 最小值
row_mini1.append(row_min)
Row.remove(row_min)
row_2nd_min = min(Row) # 次小值
row_mini2.append(row_2nd_min)
# 求解罚数
r_pun = [row_mini2[i] - row_mini1[i] for i in range(len(row_mini1))]
print('行罚数:', r_pun)
# 计算列罚数
col_mini1 = []
col_mini2 = []
for col in range(c.shape[1]):
Col = list(c[:, col])
col_min = min(Col)
col_mini1.append(col_min)
Col.remove(col_min)
col_2nd_min = min(Col)
col_mini2.append(col_2nd_min)
c_pun = [col_mini2[i] - col_mini1[i] for i in range(len(col_mini1))]
print('列罚数:', c_pun)
# 将行罚数和列罚数合并为罚数向量
pun = copy.deepcopy(r_pun)
pun.extend(c_pun)
print('罚数向量:', pun)
# 找到最大罚数及其索引
max_pun = max(pun)
max_pun_index = pun.index(max(pun))
max_pun_num = max_pun_index + 1
print('最大罚数:', max_pun, '元素序号:', max_pun_num)
# 前面是行,后面是列。这里是判断最大罚数的位置
if max_pun_num <= len(r_pun):
# 对行进行操作
row_num = max_pun_num
print('对第', row_num, '行进行操作:')
row_index = row_num - 1
catch_row = c[row_index, :]
print(catch_row)
min_cost_colindex = int(np.argwhere(catch_row == min(catch_row)))
print('最小成本所在列索引:', min_cost_colindex)
if a[row_index] <= b[min_cost_colindex]:
x[row_index, min_cost_colindex] = a[row_index]
c1 = copy.deepcopy(c)
c1[row_index, :] = [M] * c1.shape[1]
b[min_cost_colindex] -= a[row_index]
a[row_index] -= a[row_index]
else:
x[row_index, min_cost_colindex] = b[min_cost_colindex]
c1 = copy.deepcopy(c)
c1[:, min_cost_colindex] = [M] * c1.shape[0]
a[row_index] -= b[min_cost_colindex]
b[min_cost_colindex] -= b[min_cost_colindex]
else:
# 对列进行操作
col_num = max_pun_num - len(r_pun)
col_index = col_num - 1
print('对第', col_num, '列进行操作:')
catch_col = c[:, col_index]
print(catch_col)
# 寻找最大罚数所在行/列的最小成本系数
min_cost_rowindex = int(np.argwhere(catch_col == min(catch_col)))
print('最小成本所在行索引:', min_cost_rowindex)
# 计算将该位置应填入x矩阵的数值(a,b中较小值)
if a[min_cost_rowindex] <= b[col_index]:
x[min_cost_rowindex, col_index] = a[min_cost_rowindex]
c1 = copy.deepcopy(c)
c1[min_cost_rowindex, :] = [M] * c1.shape[1]
b[col_index] -= a[min_cost_rowindex]
a[min_cost_rowindex] -= a[min_cost_rowindex]
else:
x[min_cost_rowindex, col_index] = b[col_index]
# 填入后删除已满足/耗尽资源系数的行/列,得到剩余的成本矩阵,并改写资源系数
c1 = copy.deepcopy(c)
c1[:, col_index] = [M] * c1.shape[0]
a[min_cost_rowindex] -= b[col_index]
b[col_index] -= b[col_index]
c = c1
print('本次迭代后的x矩阵:\n', x)
print('a:', a)
print('b:', b)
print('c:\n', c)
if np.all(c == M):
print('【迭代完成】')
print('-' * 60)
else:
print('【迭代未完成】')
print('-' * 60)
# 计算总成本
total_cost = np.sum(np.multiply(x, cost))
# 判断运输问题类别
if np.all(a == 0):
if np.all(b == 0):
print('>>>供求平衡<<<')
else:
print('>>>供不应求,需求方有余量<<<')
elif np.all(b == 0):
print('>>>供大于求,供给方有余量<<<')
else:
print('>>>无法找到初始基可行解<<<')
print('>>>初始基本可行解x*:\n', x)
print('>>>当前总成本:', total_cost)
[m, n] = x.shape
varnum = np.array(np.nonzero(x)).shape[1]
# 根据秩来判断是否有退化解
if varnum != m + n - 1:
print('【注意:问题含有退化解】')
return (cost, x)
path = r'TP_PPT_Sample1.xlsx'
mat = pd.read_excel(path, header=None).values
# c=np.array([[3,11,3,10],[1,9,2,8],[7,4,10,5]])
# a=np.array([7,4,9])
# b=np.array([3,6,5,6])
[c, x] = TP_vogel(mat)
# [c,x]=TP_vogel([c,a,b])
运行代码结果
c:
[[ 3. 11. 3. 10.]
[ 1. 9. 2. 8.]
[ 7. 4. 10. 5.]]
行罚数: [0.0, 1.0, 1.0]
列罚数: [2.0, 5.0, 1.0, 3.0]
罚数向量: [0.0, 1.0, 1.0, 2.0, 5.0, 1.0, 3.0]
最大罚数: 5.0 元素序号: 5
对第 2 列进行操作:
[11. 9. 4.]
最小成本所在行索引: 2
本次迭代后的x矩阵:
[[0. 0. 0. 0.]
[0. 0. 0. 0.]
[0. 6. 0. 0.]]
a: [7. 4. 3.]
b: [3. 0. 5. 6.]
c:
[[3.e+00 1.e+09 3.e+00 1.e+01]
[1.e+00 1.e+09 2.e+00 8.e+00]
[7.e+00 1.e+09 1.e+01 5.e+00]]
【迭代未完成】
------------------------------------------------------------
c:
[[3.e+00 1.e+09 3.e+00 1.e+01]
[1.e+00 1.e+09 2.e+00 8.e+00]
[7.e+00 1.e+09 1.e+01 5.e+00]]
行罚数: [0.0, 1.0, 2.0]
列罚数: [2.0, 0.0, 1.0, 3.0]
罚数向量: [0.0, 1.0, 2.0, 2.0, 0.0, 1.0, 3.0]
最大罚数: 3.0 元素序号: 7
对第 4 列进行操作:
[10. 8. 5.]
最小成本所在行索引: 2
本次迭代后的x矩阵:
[[0. 0. 0. 0.]
[0. 0. 0. 0.]
[0. 6. 0. 3.]]
a: [7. 4. 0.]
b: [3. 0. 5. 3.]
c:
[[3.e+00 1.e+09 3.e+00 1.e+01]
[1.e+00 1.e+09 2.e+00 8.e+00]
[1.e+09 1.e+09 1.e+09 1.e+09]]
【迭代未完成】
------------------------------------------------------------
c:
[[3.e+00 1.e+09 3.e+00 1.e+01]
[1.e+00 1.e+09 2.e+00 8.e+00]
[1.e+09 1.e+09 1.e+09 1.e+09]]
行罚数: [0.0, 1.0, 0.0]
列罚数: [2.0, 0.0, 1.0, 2.0]
罚数向量: [0.0, 1.0, 0.0, 2.0, 0.0, 1.0, 2.0]
最大罚数: 2.0 元素序号: 4
对第 1 列进行操作:
[3.e+00 1.e+00 1.e+09]
最小成本所在行索引: 1
本次迭代后的x矩阵:
[[0. 0. 0. 0.]
[3. 0. 0. 0.]
[0. 6. 0. 3.]]
a: [7. 1. 0.]
b: [0. 0. 5. 3.]
c:
[[1.e+09 1.e+09 3.e+00 1.e+01]
[1.e+09 1.e+09 2.e+00 8.e+00]
[1.e+09 1.e+09 1.e+09 1.e+09]]
【迭代未完成】
------------------------------------------------------------
c:
[[1.e+09 1.e+09 3.e+00 1.e+01]
[1.e+09 1.e+09 2.e+00 8.e+00]
[1.e+09 1.e+09 1.e+09 1.e+09]]
行罚数: [7.0, 6.0, 0.0]
列罚数: [0.0, 0.0, 1.0, 2.0]
罚数向量: [7.0, 6.0, 0.0, 0.0, 0.0, 1.0, 2.0]
最大罚数: 7.0 元素序号: 1
对第 1 行进行操作:
[1.e+09 1.e+09 3.e+00 1.e+01]
最小成本所在列索引: 2
本次迭代后的x矩阵:
[[0. 0. 5. 0.]
[3. 0. 0. 0.]
[0. 6. 0. 3.]]
a: [2. 1. 0.]
b: [0. 0. 0. 3.]
c:
[[1.e+09 1.e+09 1.e+09 1.e+01]
[1.e+09 1.e+09 1.e+09 8.e+00]
[1.e+09 1.e+09 1.e+09 1.e+09]]
【迭代未完成】
------------------------------------------------------------
c:
[[1.e+09 1.e+09 1.e+09 1.e+01]
[1.e+09 1.e+09 1.e+09 8.e+00]
[1.e+09 1.e+09 1.e+09 1.e+09]]
行罚数: [999999990.0, 999999992.0, 0.0]
列罚数: [0.0, 0.0, 0.0, 2.0]
罚数向量: [999999990.0, 999999992.0, 0.0, 0.0, 0.0, 0.0, 2.0]
最大罚数: 999999992.0 元素序号: 2
对第 2 行进行操作:
[1.e+09 1.e+09 1.e+09 8.e+00]
最小成本所在列索引: 3
本次迭代后的x矩阵:
[[0. 0. 5. 0.]
[3. 0. 0. 1.]
[0. 6. 0. 3.]]
a: [2. 0. 0.]
b: [0. 0. 0. 2.]
c:
[[1.e+09 1.e+09 1.e+09 1.e+01]
[1.e+09 1.e+09 1.e+09 1.e+09]
[1.e+09 1.e+09 1.e+09 1.e+09]]
【迭代未完成】
------------------------------------------------------------
c:
[[1.e+09 1.e+09 1.e+09 1.e+01]
[1.e+09 1.e+09 1.e+09 1.e+09]
[1.e+09 1.e+09 1.e+09 1.e+09]]
行罚数: [999999990.0, 0.0, 0.0]
列罚数: [0.0, 0.0, 0.0, 999999990.0]
罚数向量: [999999990.0, 0.0, 0.0, 0.0, 0.0, 0.0, 999999990.0]
最大罚数: 999999990.0 元素序号: 1
对第 1 行进行操作:
[1.e+09 1.e+09 1.e+09 1.e+01]
最小成本所在列索引: 3
本次迭代后的x矩阵:
[[0. 0. 5. 2.]
[3. 0. 0. 1.]
[0. 6. 0. 3.]]
a: [0. 0. 0.]
b: [0. 0. 0. 0.]
c:
[[1.e+09 1.e+09 1.e+09 1.e+09]
[1.e+09 1.e+09 1.e+09 1.e+09]
[1.e+09 1.e+09 1.e+09 1.e+09]]
【迭代完成】
------------------------------------------------------------
>>>供求平衡<<<
>>>初始基本可行解x*:
[[0. 0. 5. 2.]
[3. 0. 0. 1.]
[0. 6. 0. 3.]]
>>>当前总成本: 85.0
下面举一个退化解的例子:
退化解指的是在计算过程中,初始基本可行解中的基变量数量少于m+n-1,其中m和n分别为运输问题的供应源和需求点的数量。换句话说,退化解是一种特殊情况,其中一些供应源和需求点没有在初始基本可行解中使用。
退化解的出现可能导致后续的迭代过程无法继续进行,因为基变量数量不足以满足问题的要求。这会影响最终解的有效性和准确性。
在退化解的情况下,通常需要采取特殊的策略来处理,以确保迭代过程的正常进行。这可能包括修改初始基本可行解或应用其他算法来解决问题。
一运输问题的运输表如下:

将以上表格保存为 TP_Text_5.9.xlsx,在 Python 中求解。程序运行的最终结果为:
>>>供求平衡<<<
>>>初始基本可行解x*:
[[1. 0. 0. 0. 0.]
[0. 0. 1. 0. 0.]
[0. 0. 0. 1. 0.]
[0. 0. 0. 0. 1.]
[0. 1. 0. 0. 0.]]
>>>当前总成本: 0.8999999999999999
【注意:问题含有退化解】
最终得到的初始基可行解只含有 5 个非零变量,而 (m+n-1)=9,可见发生了退化。
2.3.2 位势法判断最优解
在实现伏格尔法的基础上添加下列函数,以及函数调用sigma=TP_potential(c,x)。
def create_c_nonzeros(c, x):
"""
根据运输问题中的需求矩阵x创建一个与成本矩阵c相同形状的新矩阵c_nonzeros,其中非零元素与x相对应位置上的元素相乘,而零元素仍保持为零。
"""
import numpy as np
import copy
nonzeros = copy.deepcopy(x)
for i in range(x.shape[0]):
for j in range(x.shape[1]):
if x[i, j] != 0:
nonzeros[i, j] = 1
# print(nonzeros)
c_nonzeros = np.multiply(c, nonzeros)
return c_nonzeros
def if_dsquare(a, b):
"""
函数if_dsquare用于判断位势方程组是否可解。
根据输入的系数矩阵a和值向量b,函数检查矩阵的维度和条件来判断是否可解。
如果位势方程组可解,则返回True;如果不可解,则返回False。
:param a: 系数矩阵a
:param b: 值向量b
:return: 位势方程组可解,为True
"""
print('a:', a.shape, '\n', 'b:', b.shape)
correct = '>>>位势方程组可解<<<'
error = '>>>位势方程组不可解,请检查基变量个数是否等于(m+n-1)及位势未知量个数是否等于(m+n)<<<'
if len(a.shape) == 2:
if len(b.shape) == 2:
if a.shape[0] == a.shape[1] and a.shape == b.shape:
print(correct)
if_dsquare = True
else:
print(error)
if_dsquare = False
elif len(b.shape) == 1 and b.shape[0] != 0:
if a.shape[0] == a.shape[1] and a.shape[0] == b.shape[0]:
print(correct)
if_dsquare = True
else:
print(error)
if_dsquare = False
else:
print(error)
if_dsquare = False
elif len(a.shape) == 1:
if len(b.shape) == 2:
if b.shape[0] == b.shape[1] and a.shape[0] == b.shape[0]:
print('>>>位势方程组系数矩阵与方程组值向量位置错误<<<')
if_dsquare = 'True but not solvable'
else:
print(error)
if_dsquare = False
elif len(b.shape) == 1:
print(error)
if_dsquare = False
else:
print(error)
if_dsquare = False
else:
print(error)
if_dsquare = False
return if_dsquare
def TP_potential(cost, x):
"""
运输问题的位势法求解函数。首先,它计算变量的数量varnum,如果varnum不等于m + n - 1(基变量的数量),
则表示问题存在退化解,将返回None,并输出相应的提示信息。如果varnum满足条件,则继续进行位势法的计算。
:param cost: 成本矩阵cost
:param x: 需求矩阵x
:return:
"""
[m, n] = x.shape
varnum = np.array(np.nonzero(x)).shape[1]
if varnum != m + n - 1:
sigma = None
print('【问题含有退化解,暂时无法判断最优性】')
else:
# print(c_nonzeros.shape)
c_nonzeros = create_c_nonzeros(c, x)
cc_nonzeros = np.array(np.nonzero(c_nonzeros))
A = []
B = []
length = c_nonzeros.shape[0] + c_nonzeros.shape[1]
zeros = np.zeros((1, length))[0]
for i in range(cc_nonzeros.shape[1]):
zeros = np.zeros((1, length))[0]
zeros[cc_nonzeros[0, i]] = 1
zeros[cc_nonzeros[1, i] + c_nonzeros.shape[0]] = 1
A.append(zeros)
B.append(c_nonzeros[cc_nonzeros[0, i], cc_nonzeros[1, i]])
l = [1]
for j in range(length - 1):
l.append(0) # 补充一个x1=0的方程以满足求解条件
A.append(l)
B.append(0)
# print(A)
# print(B)
A = np.array(A)
B = np.array(B)
judge = if_dsquare(A, B)
if judge == True:
sol = np.linalg.solve(A, B) # 求解条件:A的行数(方程个数)=A的列数(变量个数)=B的个数(方程结果个数)才能解
# print(sol)
var = [] # 创建位势名称数组
for i in range(c_nonzeros.shape[0]):
var.append('u' + str(i + 1))
for j in range(c_nonzeros.shape[1]):
var.append('v' + str(j + 1))
# print(var)
solset = dict(zip(var, sol))
print('>>>当前位势:\n', solset)
u = []
v = []
[m, n] = c_nonzeros.shape
zero_places = np.transpose(np.argwhere(c_nonzeros == 0))
for i in range(m):
u.append(sol[i])
for j in range(n):
v.append(sol[j + m])
for k in range(zero_places.shape[1]):
c_nonzeros[zero_places[0, k], zero_places[1, k]] = u[zero_places[0, k]] + v[zero_places[1, k]]
# print(c_nonzeros)
sigma = cost - c_nonzeros
print('>>>检验表σ:\n', sigma)
if np.all(sigma >= 0):
print('>>>TP已达到最优解<<<')
else:
print('>>>TP未达到最优解<<<')
else:
sigma = None
print('>>>位势方程组不可解<<<')
return sigma
结果
c:
[[ 3. 11. 3. 10.]
[ 1. 9. 2. 8.]
[ 7. 4. 10. 5.]]
行罚数: [0.0, 1.0, 1.0]
列罚数: [2.0, 5.0, 1.0, 3.0]
罚数向量: [0.0, 1.0, 1.0, 2.0, 5.0, 1.0, 3.0]
最大罚数: 5.0 元素序号: 5
对第 2 列进行操作:
[11. 9. 4.]
最小成本所在行索引: 2
本次迭代后的x矩阵:
[[0. 0. 0. 0.]
[0. 0. 0. 0.]
[0. 6. 0. 0.]]
a: [7. 4. 3.]
b: [3. 0. 5. 6.]
c:
[[3.e+00 1.e+09 3.e+00 1.e+01]
[1.e+00 1.e+09 2.e+00 8.e+00]
[7.e+00 1.e+09 1.e+01 5.e+00]]
【迭代未完成】
------------------------------------------------------------
c:
[[3.e+00 1.e+09 3.e+00 1.e+01]
[1.e+00 1.e+09 2.e+00 8.e+00]
[7.e+00 1.e+09 1.e+01 5.e+00]]
行罚数: [0.0, 1.0, 2.0]
列罚数: [2.0, 0.0, 1.0, 3.0]
罚数向量: [0.0, 1.0, 2.0, 2.0, 0.0, 1.0, 3.0]
最大罚数: 3.0 元素序号: 7
对第 4 列进行操作:
[10. 8. 5.]
最小成本所在行索引: 2
本次迭代后的x矩阵:
[[0. 0. 0. 0.]
[0. 0. 0. 0.]
[0. 6. 0. 3.]]
a: [7. 4. 0.]
b: [3. 0. 5. 3.]
c:
[[3.e+00 1.e+09 3.e+00 1.e+01]
[1.e+00 1.e+09 2.e+00 8.e+00]
[1.e+09 1.e+09 1.e+09 1.e+09]]
【迭代未完成】
------------------------------------------------------------
c:
[[3.e+00 1.e+09 3.e+00 1.e+01]
[1.e+00 1.e+09 2.e+00 8.e+00]
[1.e+09 1.e+09 1.e+09 1.e+09]]
行罚数: [0.0, 1.0, 0.0]
列罚数: [2.0, 0.0, 1.0, 2.0]
罚数向量: [0.0, 1.0, 0.0, 2.0, 0.0, 1.0, 2.0]
最大罚数: 2.0 元素序号: 4
对第 1 列进行操作:
[3.e+00 1.e+00 1.e+09]
最小成本所在行索引: 1
本次迭代后的x矩阵:
[[0. 0. 0. 0.]
[3. 0. 0. 0.]
[0. 6. 0. 3.]]
a: [7. 1. 0.]
b: [0. 0. 5. 3.]
c:
[[1.e+09 1.e+09 3.e+00 1.e+01]
[1.e+09 1.e+09 2.e+00 8.e+00]
[1.e+09 1.e+09 1.e+09 1.e+09]]
【迭代未完成】
------------------------------------------------------------
c:
[[1.e+09 1.e+09 3.e+00 1.e+01]
[1.e+09 1.e+09 2.e+00 8.e+00]
[1.e+09 1.e+09 1.e+09 1.e+09]]
行罚数: [7.0, 6.0, 0.0]
列罚数: [0.0, 0.0, 1.0, 2.0]
罚数向量: [7.0, 6.0, 0.0, 0.0, 0.0, 1.0, 2.0]
最大罚数: 7.0 元素序号: 1
对第 1 行进行操作:
[1.e+09 1.e+09 3.e+00 1.e+01]
最小成本所在列索引: 2
本次迭代后的x矩阵:
[[0. 0. 5. 0.]
[3. 0. 0. 0.]
[0. 6. 0. 3.]]
a: [2. 1. 0.]
b: [0. 0. 0. 3.]
c:
[[1.e+09 1.e+09 1.e+09 1.e+01]
[1.e+09 1.e+09 1.e+09 8.e+00]
[1.e+09 1.e+09 1.e+09 1.e+09]]
【迭代未完成】
------------------------------------------------------------
c:
[[1.e+09 1.e+09 1.e+09 1.e+01]
[1.e+09 1.e+09 1.e+09 8.e+00]
[1.e+09 1.e+09 1.e+09 1.e+09]]
行罚数: [999999990.0, 999999992.0, 0.0]
列罚数: [0.0, 0.0, 0.0, 2.0]
罚数向量: [999999990.0, 999999992.0, 0.0, 0.0, 0.0, 0.0, 2.0]
最大罚数: 999999992.0 元素序号: 2
对第 2 行进行操作:
[1.e+09 1.e+09 1.e+09 8.e+00]
最小成本所在列索引: 3
本次迭代后的x矩阵:
[[0. 0. 5. 0.]
[3. 0. 0. 1.]
[0. 6. 0. 3.]]
a: [2. 0. 0.]
b: [0. 0. 0. 2.]
c:
[[1.e+09 1.e+09 1.e+09 1.e+01]
[1.e+09 1.e+09 1.e+09 1.e+09]
[1.e+09 1.e+09 1.e+09 1.e+09]]
【迭代未完成】
------------------------------------------------------------
c:
[[1.e+09 1.e+09 1.e+09 1.e+01]
[1.e+09 1.e+09 1.e+09 1.e+09]
[1.e+09 1.e+09 1.e+09 1.e+09]]
行罚数: [999999990.0, 0.0, 0.0]
列罚数: [0.0, 0.0, 0.0, 999999990.0]
罚数向量: [999999990.0, 0.0, 0.0, 0.0, 0.0, 0.0, 999999990.0]
最大罚数: 999999990.0 元素序号: 1
对第 1 行进行操作:
[1.e+09 1.e+09 1.e+09 1.e+01]
最小成本所在列索引: 3
本次迭代后的x矩阵:
[[0. 0. 5. 2.]
[3. 0. 0. 1.]
[0. 6. 0. 3.]]
a: [0. 0. 0.]
b: [0. 0. 0. 0.]
c:
[[1.e+09 1.e+09 1.e+09 1.e+09]
[1.e+09 1.e+09 1.e+09 1.e+09]
[1.e+09 1.e+09 1.e+09 1.e+09]]
【迭代完成】
------------------------------------------------------------
>>>供求平衡<<<
>>>初始基本可行解x*:
[[0. 0. 5. 2.]
[3. 0. 0. 1.]
[0. 6. 0. 3.]]
>>>当前总成本: 85.0
>>>位势方程组可解<<<
>>>当前位势:
{'u1': 0.0, 'u2': -2.0, 'u3': -5.0, 'v1': 3.0, 'v2': 9.0, 'v3': 3.0, 'v4': 10.0}
>>>检验数表σ:
[[ 0. 2. 0. 0.]
[ 0. 2. 1. 0.]
[ 9. 0. 12. 0.]]
>>>TP已达到最优解<<<
退化现象的问题暂时不可解。
>>>供求平衡<<<
>>>初始基本可行解x*:
[[1. 0. 0. 0. 0.]
[0. 0. 1. 0. 0.]
[0. 0. 0. 1. 0.]
[0. 0. 0. 0. 1.]
[0. 1. 0. 0. 0.]]
>>>当前总成本: 0.8999999999999999
【注意:问题含有退化解】
【问题含有退化解,暂时无法判断最优性】
参考资料:
运筹学 第4版 钱颂迪 清华大学出版社
https://zhuanlan.zhihu.com/p/448725456
https://blog.csdn.net/m0_46927406/article/details/109903843
https://blog.csdn.net/m0_46927406/article/details/110070154