文章目录
- 01背包 - 问题分析
- 01背包题目
- 第一问
- 1. 状态表示
- 2. 分析状态转移方程
- 3. 初始化
- 4. 填表顺序
- 5. 返回值
- 第二问
- 1. 状态表示
- 2. 状态转移⽅程
- 3. 初始化
- 4. 填表顺序
- 5. 返回值
- C++运行代码
01背包 - 问题分析
01背包是指在一个有容积限制(或者重量限制)的背包中放入物品,物品拥有体积、重量和价值等属性。需要求一种满足背包限制的放置物品的方式,使得背包中物品的价值之和最大。比如有n件物品和一个最多能背重量为w 的背包。第i件物品的重量是weight[i],得到的价值是value[i] 。每件物品只能用一次,求解将哪些物品装入背包里物品价值总和最大。

在01背包问题中,每种物品仅有一件,可以选择放或不放。这是背包问题中最简单的一种,也是动态规划的经典问题之一。
- 在下面的讲解中,我举一个例子:
背包最大重量为5.
物品为:
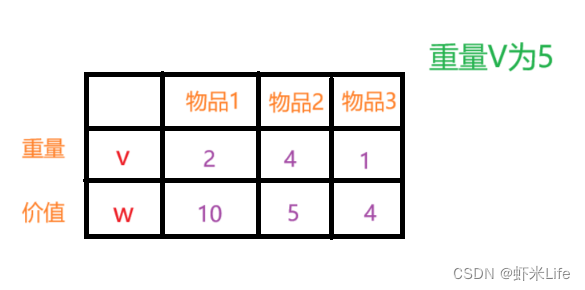
- 问背包能背的物品最大价值是多少?
此时发现物品1 + 物品3 的重量为3 价值为14。 此时这是我们最大价值
- 若背包恰好装满,求至多能装多大价值的物品是多少?
此时发现物品1 + 物品3 的重量为3 价值为14. 但是重量没有恰好装满,不符合题意.
我们在看物品2 + 物品3 的重量为5,价值为9. 重量恰好装满,且是我们这里的最大价值
01背包题目
【模板】01背包_牛客题霸_牛客网 (nowcoder.com)
动规五部曲分析:
- 分析状态表示
- 分析状态转移方程
- 初始化
- 填表顺序
- 返回值
第一问
- 问背包能背的物品最大价值是多少
1. 状态表示
我们看看这个状态表示
dp[i] 表示: 从前 i 个物品中选,所有选法中,能挑选出来的最大价值.
相信很多同学第一时间是想出的是这个状态表示,但你们仔细想一下,我们的体积呢?这个状态表示体积可能会超出题目给定的范围,所有这个状态表示是错.我们必须换一种状态表示,我们换一个二维的数组,加多一维表示体积.
dp[i][j] 表⽰:从前 i 个物品中挑选,总体积「不超过J」 ,所有的选法中,能挑选出来的最⼤价值。
v表示体积,w表示价值
要时刻记着这个dp数组的含义,下面的一些步骤都围绕这dp数组的含义进行的,如果哪里看懵了,就来回顾一下i代表什么,j又代表什么。
2. 分析状态转移方程
- 线性 dp 状态转移⽅程分析⽅式,⼀般都是根据「最后⼀步」的状况,来分情况讨论:
- 如果不放第i个物品的值
最后⼀步如果不选第 i 个物品.相当于就是去前 i - 1 个物品中挑选,并且总体积不超过 j
其实就是当物品i的重量大于背包j的重量时,物品i无法放进背包中,所以背包内的价值依然和前面相同。
- 如果选择第i个物品
那么我就只能去前 i - 1 个物品中,挑选总体积不超过 j - v[i]的物品,。此时
dp[i][j] = dp[i - 1][j - v[i]] + w[i] 。因此需要特判⼀下j >= v[i],因为要留⾜够的体积装这个第 i 个物品。综上,状态转移⽅程为:dp[i][j] = max(dp[i 1][j], dp[i - 1][j - v[i]] +w[i])如果没看懂回顾一下状态表示, dp[i][j] 表⽰:从前 i 个物品中挑选,总体积「不超过J」 ,所有的选法中,能挑选出来的最⼤价值。
综上,状态转移⽅程为:
dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - v[i]] + w[i]),但需要特判一下 dp[i - 1][j - v[i]] + w[i])` 是否存在.
3. 初始化
- 初始化的意义就是让我填表时候不越界,需要我们需要对边界条件处理一下.
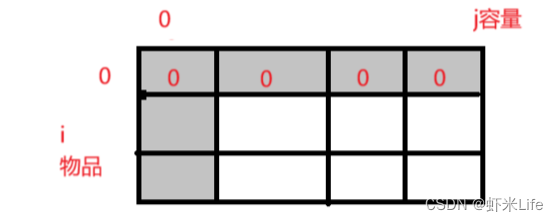
我们多加⼀⾏,⽅便我们的初始化
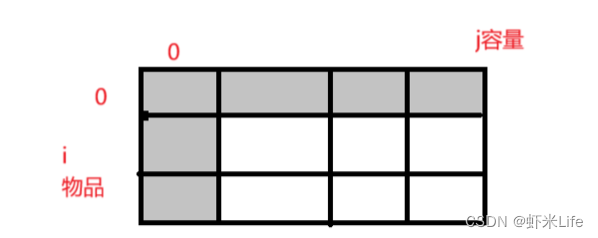
- 第一个位置
i 是物品 ,从 0 号位置开始选,但是没有 0 号位置,因为物品是从 1 到 n的,所有填 0。
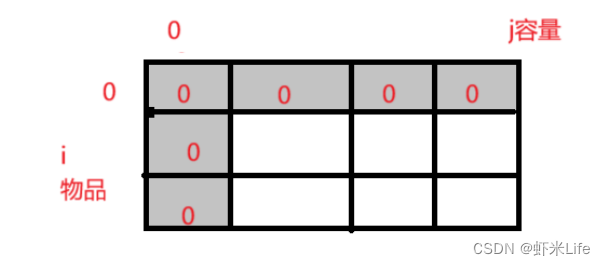
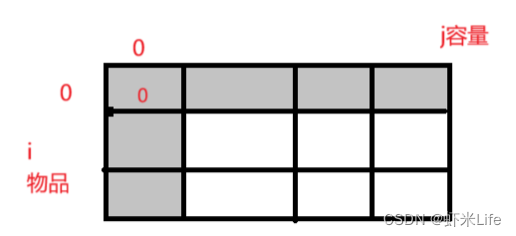
- 第一行
从 0 号位置开始选,容量不超过 0,此时仅需将第⼀⾏初始化为 0 即可。因为什么也不选,也能满⾜体积不⼩于 j 的情况,此时的价值为 0 。
- 我们讨论第 0 竖的情况,讨论 j,容量不超过 0,物品总是有体积,所以全部都不
选,初始化成 0.
4. 填表顺序
根据「状态转移⽅程」,我们仅需「从上往下」填表即可。
5. 返回值
我们看看状态转移⽅程
从前 i 个物品中挑选,最⼤价值总体积不超过 j,所有的选法中,能挑选出来的最⼤价值。根据「状态表⽰」,返回 dp[n][V] 。
第二问
- 若背包恰好装满,求至多能装多大价值的物品是多少?
其实第⼆问仅需微调⼀下 dp 过程的五步即可。
1. 状态表示
还是跟之前一样
dp[i][j] 表⽰:从前 i 个物品中挑选,总体积正好等于 j ,所有的选法中,能挑选出来的最⼤价值。
2. 状态转移⽅程
- 线性 dp 状态转移⽅程分析⽅式,⼀般都是根据「最后⼀步」的状况,来分情况讨论:
我们的dp[i-1][j]不一定存在 , 因为有可能凑不⻬ j 体积的物品,因此我们把不合法的状态设置为 -1 。不能等于0,因为0是代表没有物品选.
- 其实分析情况跟第一问差不多,但是要注意细节
- 如果不放第i个物品的值
最后一步如果不选第i个物品.相当于就是去前 i - 1 个物品中挑选此时, 这个无需判断是否是-1,因为在
dp[i][j]这种情况是一定存在的,所有我们的dp[i][j]可以先等于dp[i-1][j].如果dp[i-1][j]是等于-1的话,那没关系,你选不了我也选不了,你从i-1个物品想凑成一个j,我这种情况也凑不成j,所有不用判断dp[i][j] = dp[i -1][ j ]
- 如果选择第i个物品
在使⽤
dp[i][j - v[i]]的时候,不仅要判断j >= v[i],⼜要判断dp[i][j -
v[i]]表⽰的情况是否合法,也就是dp[i][j - v[i]] != -1。
综上,状态转移⽅程为:
dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - v[i]] + w[i]),但是在使⽤dp[i - 1][j - v[i]]的时候,要判断j >= v[i],因为要留⾜够的体积装这个第 i 个物品。,⼜要判断dp[i - 1][j - v[i]]表⽰的情况是否合法,也就是dp[i - 1][j - v[i]] != -1
3. 初始化
- 初始化的意义就是让我填表时候不越界,需要我们需要对边界条件处理一下.
跟之前一样我们多加⼀⾏,⽅便我们的初始化
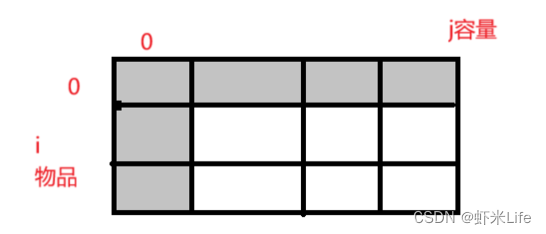
- 第一个位置
跟之前一样第一个物品是0的位置,容量为0,正好不选就可以了,所有初始化成0.
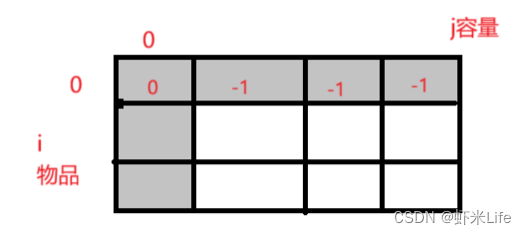
- 第一行
没有物品想凑成容量为1-n 那是不可能的,因为没有物品哪里的体积,那就是非法的,所有填-1
- 我们讨论第 0 竖的情况, 这个状态可以根据状态转移方程推导而出,当然判断条件
j ≥ v[i]为false不会进去
4. 填表顺序
根据状态转移⽅程,我们仅需从上往下填表即可。
5. 返回值
我们看看状态转移⽅程
从前 i 个物品中挑选,最⼤价值总体积不超过 j,所有的选法中,能挑选出来的最⼤价值。根据「状态表⽰」,返回dp[n][V]。但是由于最后可能凑不成体积为 V 的情况,因此返回之前需要「特判」⼀下。
C++运行代码
#include <iostream>
#include <string.h>
using namespace std;
const int N = 1010;
int n, V, v[N], w[N];
int dp[N][N];
int main()
{
// 读⼊数据
cin >> n >> V;
for (int i = 1; i <= n; i++)
cin >> v[i] >> w[i];
// 解决第⼀问
for (int i = 1; i <= n; i++)
for (int j = 0; j <= V; j++) // 修改遍历顺序
{
dp[i][j] = dp[i - 1][j];
if (j >= v[i])
dp[i][j] = max(dp[i][j], dp[i - 1][j - v[i]] + w[i]);
}
cout << dp[n][V] << endl;
// 解决第⼆问
memset(dp, 0, sizeof dp);
for (int j = 1; j <= V; j++) dp[0][j] = -1; //初始化
for (int i = 1; i <= n; i++)
for (int j = 0; j <= V; j++) // 修改遍历顺序
{
dp[i][j] = dp[i - 1][j];
if (j >= v[i] && dp[i - 1][j - v[i]] != -1)
dp[i][j] = max(dp[i][j], dp[i - 1][j - v[i]] + w[i]);
}
//由于最后可能凑不成体积为 V 的情况,因此返回之前需要特判⼀下。
cout << (dp[n][V] == -1 ? 0 : dp[n][V]) << endl;
return 0;
}