用javascript分类刷leetcode10.递归分治(图文视频讲解)

news2024/11/23 12:32:49

递归三要素

  • 递归函数以及参数
  • 递归终止条件
  • 递归单层搜索逻辑

递归伪代码模版：

function recursion(level, param1, param2, ...) {
  //递归终止条件
  if (level > MAX_LEVEL) {
    // output result
    return;
  }

  //处理当前层
  process_data(level, data, ...);

  //进入下一层
  recursion(level + 1, p1, ...);

  //重置状态
  reverse_state(level);
}

什么是分治：

分治会将大问题拆解成小问题，拆解到最小问题之后，开始不断合并结果，递归是分治实现的一种形式或者是分治实现的一部分，分治包括三分部分，分解、计算、合并。分治的场景很多，例如快速排序，归并排序。

ds_49

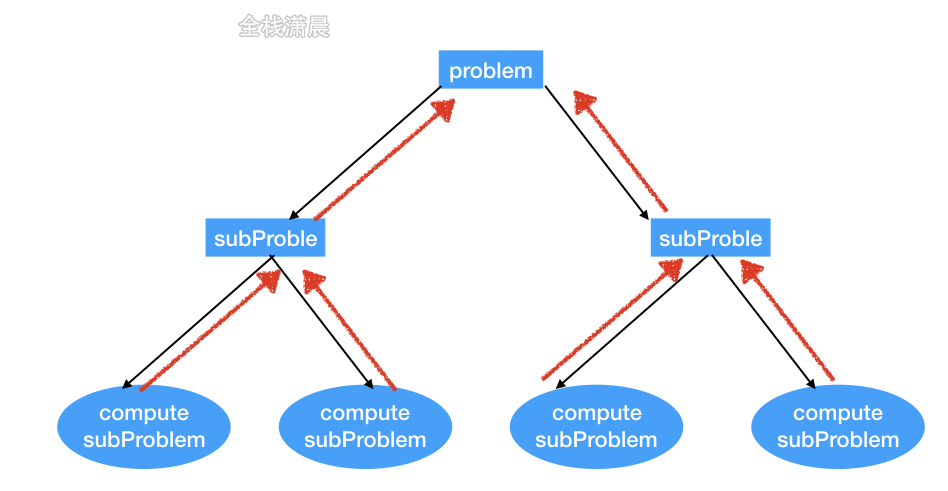
分治伪代码模版：

function divide_conquer(problem, param1, param2, ...){
  if(problem === null){
    // return result
  }

  //分割问题
  subproblem = split_problem(problem, data)

  //计算子问题
  subResult1 = divide_conquer(subproblem[0], p1, ...)
  subResult2 = divide_conquer(subproblem[1], p1, ...)
  subResult3 = divide_conquer(subproblem[2], p1, ...)
  ...

  result = process_resule(subResult1, subResult2, subResult3,...)
}

举例

计算n! n! = 1 * 2 * 3... * n

function factorial(n) {
  if (n <= 1) return 1;
  return n * factorial(n - 1);
}

factorial(6);
6 * factorial(5);
6 * 5 * factorial(4);
//...
6 * 5 * 4 * 3 * 2 * factorial(1);
6 * 5 * 4 * 3 * 2 * 1;
6 * 5 * 4 * 3 * 2;
//...
6 * 120;
720;

斐波那契数列，F(n)=F(n-1)+F(n+2)

function fib(n) {
  if (n === 0 || n === 1) {
    return n;
  }
  return fib(n - 1) + fib(n - 2);
}

53. 最大子序和 （easy）

给你一个整数数组 nums ，请你找出一个具有最大和的连续子数组（子数组最少包含一个元素），返回其最大和。

子数组 是数组中的一个连续部分。

示例 1：

输入：nums = [-2,1,-3,4,-1,2,1,-5,4]
输出：6
解释：连续子数组 [4,-1,2,1] 的和最大，为 6 。
示例 2：

输入：nums = [1]
输出：1
示例 3：

输入：nums = [5,4,-1,7,8]
输出：23

提示：

1 <= nums.length <= 105
-104 <= nums[i] <= 104

进阶：如果你已经实现复杂度为 O(n) 的解法，尝试使用更为精妙的 分治法 求解。

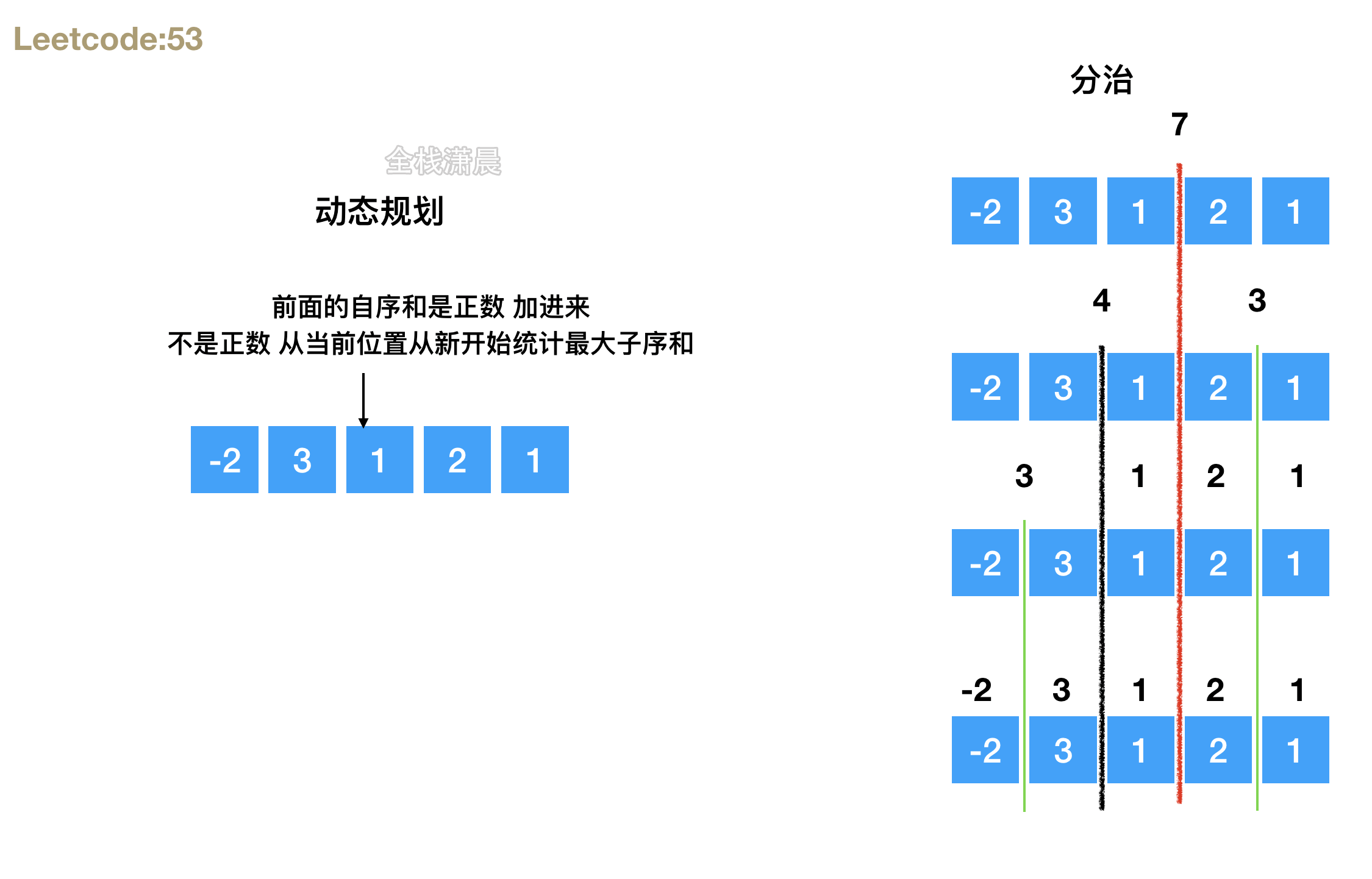
ds_159

方法1:动态规划
  • 思路：当前最大子序和只和前面的子序和相关，循环数组，不断更新最大子序和
  • 复杂度：时间复杂度O(n)，空间复杂度O(1)

js：

var maxSubArray = function(nums) {
    const dp = [];
    let res = (dp[0] = nums[0]);//初始化状态
    for (let i = 1; i < nums.length; ++i) {
        dp[i] = nums[i];
        if (dp[i - 1] > 0) {//前面的状态是正数 则加上
            dp[i] += dp[i - 1];
        }
        res = Math.max(res, dp[i]);//更新最大值
    }
    return res;
};

//状态压缩
var maxSubArray = function(nums) {
    let pre = 0, maxAns = nums[0];
    nums.forEach((x) => {
        pre = Math.max(pre + x, x);
        maxAns = Math.max(maxAns, pre);
    });
    return maxAns;
};
方法2.分治
  • 思路：不断分割，直到每个部分是一个数字为止，然后不断合并，返回左右和左右合并之后，3个最大子序和中的最大的一个
  • 复杂度：时间复杂度O(nlogn)，二分复杂度O(logn)，二分之后每一层统计左右和合并之后的最大子序和复杂度是O(n)，所以之后的复杂度是O(nlogn)。空间复杂度O(logn)，递归的栈空间，因为是二分，每次数据规模减半

js：

function crossSum(nums, left, right, mid) {
    if (left === right) {//左右相等 返回左边的值
        return nums[left];
    }

    let leftMaxSum = Number.MIN_SAFE_INTEGER;//左边最大值初始化
    let leftSum = 0;
    for (let i = mid; i >= left; --i) {
        leftSum += nums[i];
        leftMaxSum = Math.max(leftMaxSum, leftSum);//更新左边最大子序和
    }

    let rightMaxSum = Number.MIN_SAFE_INTEGER;
    let rightSum = 0;
    for (let i = mid + 1; i <= right; ++i) {
        rightSum += nums[i];
        rightMaxSum = Math.max(rightMaxSum, rightSum);//更新右边最大子序和
    }

    return leftMaxSum + rightMaxSum;//返回左右合并之后的最大子序和
}

function _maxSubArray(nums, left, right) {
    if (left === right) {//递归终止条件
        return nums[left];
    }

    const mid = Math.floor((left + right) / 2);
    const lsum = _maxSubArray(nums, left, mid);//左边最大子序和
    const rsum = _maxSubArray(nums, mid + 1, right);//右边最大子序和
    const cross = crossSum(nums, left, right, mid);//合并左右的之后的最大子序和

    return Math.max(lsum, rsum, cross);//返回3中子序和中最大的
}

var maxSubArray = function(nums) {
    return _maxSubArray(nums, 0, nums.length - 1);
};

50. Pow(x, n) (medium)

实现 pow(x, n) ，即计算 x 的整数 n 次幂函数（即，xn ）。

示例 1：

输入：x = 2.00000, n = 10
输出：1024.00000
示例 2：

输入：x = 2.10000, n = 3
输出：9.26100
示例 3：

输入：x = 2.00000, n = -2
输出：0.25000
解释：2-2 = 1/22 = 1/4 = 0.25

提示：

-100.0 < x < 100.0
-231 <= n <= 231-1
-104 <= xn <= 104

方法1：分治

ds_66

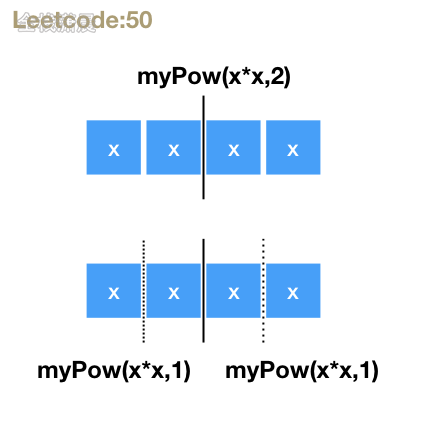
  • 思路：当n是偶数的时候，对n进行分治，拆解为x*x的n/2的次方，当n为奇数的时候拆分成x * myPow(x,n-1),注意当n是负数或者是0的特殊情况
  • 复杂度分析：时间复杂度：O(logn)， n是进行二进制拆分的时间复杂度。空间复杂度：O(logn), n为递归深度

js：

var myPow = function (x, n) {
    if (n === 0) return 1 // n=0直接返回1
    if (n < 0) {                   //n<0时 x的n次方等于1除以x的-n次方分
        return 1 / myPow(x, -n)
    }
    if (n % 2) {    //n是奇数时 x的n次方 = x*x的n-1次方
        return x * myPow(x, n - 1)
    }
    return myPow(x * x, n / 2) //n是偶数，使用分治，一分为二，等于x*x的n/2次方 
}
方法2：二进制

ds_50

  • 思路：对n的二进制不断右移动，判断n的二进制最后一位是否是1， 如果是1则将结果乘以x。
  • 复杂度分析：时间复杂度O(logn)： n为对 n 进行二进制拆分的时间复杂度，空间复杂度O(1)

js:

var myPow = function (x, n) {
    if (n < 0) {
        x = 1 / x;
        n = -n;
    }
    let result = 1;
    while (n) {
        if (n & 1) result *= x;  //判断n的二进制最后一位是否是1， 如果是1则将结果乘以x
        x *= x;
        n >>>= 1;
        //进行无符号右移1位，此处不能使用有符号右移（>>）
        //当n为-2^31转换成正数时的二进制位“10000000000000000000000000000000” , 
          //如果采用有符号右移时会取最左侧的数当符号即（1），所以返回的结果是 -1073741824
        /*
          C++ 中只有一种右移运算符——>>。它的定义如下：移出的低位舍弃；
          如果是无符号数，高位补0；如果是有符号数，高位补符号位。
          而JavaScript中有两种右移运算符——>>和>>>。其中>>是有符号右移，
          即高位补符号位（可能会出现负数变正数，正数变负数的异常情况）；>>>是无符号右移，高位无脑补0。
        */
    }
    return result;
}

124. 二叉树中的最大路径和 (hard)

路径 被定义为一条从树中任意节点出发，沿父节点-子节点连接，达到任意节点的序列。同一个节点在一条路径序列中 至多出现一次 。该路径 至少包含一个 节点，且不一定经过根节点。

路径和 是路径中各节点值的总和。

给你一个二叉树的根节点 root ，返回其 最大路径和 。

示例 1：

输入：root = [1,2,3]
输出：6
解释：最优路径是 2 -> 1 -> 3 ，路径和为 2 + 1 + 3 = 6
示例 2：

输入：root = [-10,9,20,null,null,15,7]
输出：42
解释：最优路径是 15 -> 20 -> 7 ，路径和为 15 + 20 + 7 = 42

提示：

树中节点数目范围是 [1, 3 * 104]
-1000 <= Node.val <= 1000

方法1.递归

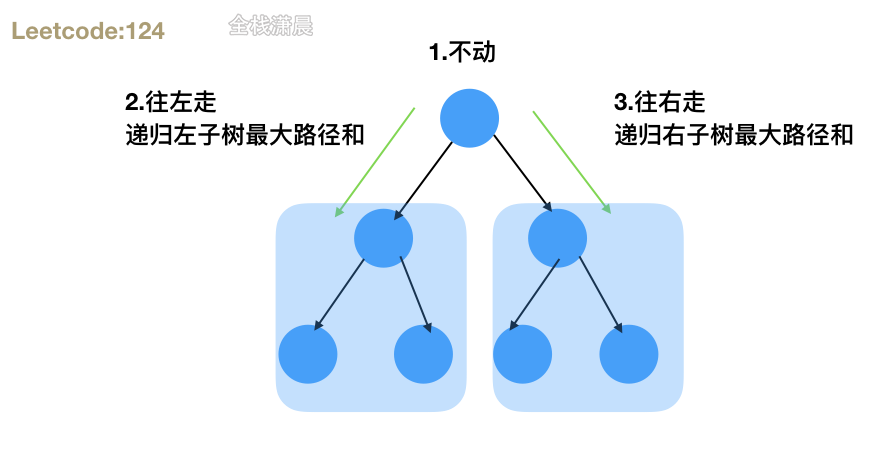
ds_107

  • 思路：从根节点递归，每次递归分为走左边、右边、不动 3种情况，用当前节点加上左右子树最大路径和不断更新最大路径和
  • 复杂度：时间复杂度O(n)，n为树的节点个数。空间复杂度O(n)，递归深度，最差情况下为数的节点数

js：

const maxPathSum = (root) => {
    let maxSum = Number.MIN_SAFE_INTEGER;//初始化最大路径和

    const dfs = (root) => {
        if (root == null) {//遍历节点是null 返回0
           return 0;
        }
        const left = dfs(root.left);   //递归左子树最大路径和
        const right = dfs(root.right); //递归右子树最大路径和

        maxSum = Math.max(maxSum, left + root.val + right);      //更新最大值

          //返回当前子树的路径和 分为走左边、右边、不动 3种情况
        const pathSum = root.val + Math.max(0, left, right);
        return pathSum < 0 ? 0 : pathSum;
    };

    dfs(root);

    return maxSum; 
};

169. 多数元素（easy）

给定一个大小为 n 的数组 nums ，返回其中的多数元素。多数元素是指在数组中出现次数 大于 ⌊ n/2 ⌋ 的元素。

你可以假设数组是非空的，并且给定的数组总是存在多数元素。

示例 1：

输入：nums = [3,2,3]
输出：3
示例 2：

输入：nums = [2,2,1,1,1,2,2]
输出：2

提示：
n == nums.length
1 <= n <= 5 * 104
-109 <= nums[i] <= 109

进阶：尝试设计时间复杂度为 O(n)、空间复杂度为 O(1) 的算法解决此问题。

方法1.排序
  • 思路：排序数组，如果有一个数字出现的频率大于n/2，则在数组nums.length / 2的位置就是这个数
  • 复杂度分析：时间复杂度：O(nlogn)，快排的时间复杂度。空间复杂度：O(logn)，排序需要logn的空间复杂度

js：

var majorityElement = function (nums) {
    nums.sort((a, b) => a - b);
    return nums[Math.floor(nums.length / 2)];
};
方法2.哈希表
  • 思路：循环数组，用哈希表存储数字和对应的个数，如果数字出现的个数大于n/2则返回这个数
  • 复杂度分析：时间复杂度：O(n)，n为nums数组的长度。空间复杂度：O(n），哈希表需要的空间

js:

var majorityElement = function (nums) {
    let half = nums.length / 2;
    let obj = {};
    for (let num of nums) {
        obj[num] = (obj[num] || 0) + 1;
        if (obj[num] > half) return num;
    }
};
方法3:抵消

js：

//[1,1,2,2,2]
const majorityElement = nums => {
    let count = 1;
    let majority = nums[0];
    for (let i = 1; i < nums.length; i++) {
        if (count === 0) {
            majority = nums[i];
        }
        if (nums[i] === majority) {
            count++;
        } else {
            count--;
        }
    }
    return majority;
};
方法4.分治

ds_51

  • 思路：不断从数组的中间进行递归分割，直到每个区间的个数是1，然后向上合并左右区间个数较多的数，向上返回。
  • 复杂度分析：时间复杂度：O(nlogn)，不断二分，复杂度是logn，二分之后每个区间需要线性统计left与right的个数，复杂度是n。空间复杂度：O(logn)，递归栈的消耗，不断二分。

Js:

var majorityElement = function (nums) {
    const getCount = (num, lo, hi) => {//统计lo到hi之间num的数量
        let count = 0;

        for (let i = lo; i <= hi; i++) {
            if (nums[i] === num) count++;
        }

        return count;
    };

    const getMode = (lo, hi) => {
        if (lo === hi) return nums[lo];

          //拆分成更小的区间
        let mid = Math.floor((lo + hi) / 2);
        let left = getMode(lo, mid);
        let right = getMode(mid + 1, hi);

        if (left === right) return left;

        let leftCount = getCount(left, lo, hi);//统计区间内left的个数
        let rightCount = getCount(right, lo, hi);//统计区间内right的个数

        return leftCount > rightCount ? left : right;//返回left和right中个数多的那个
    };

    return getMode(0, nums.length - 1);
};

938. 二叉搜索树的范围和 (easy)

给定二叉搜索树的根结点 root，返回值位于范围 [low, high] 之间的所有结点的值的和。

示例 1：

输入：root = [10,5,15,3,7,null,18], low = 7, high = 15
输出：32
示例 2：

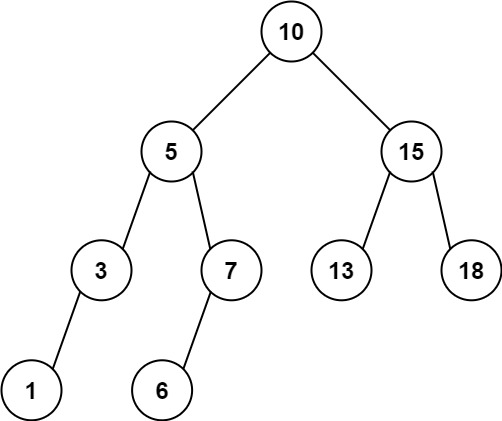
输入：root = [10,5,15,3,7,13,18,1,null,6], low = 6, high = 10
输出：23

提示：

树中节点数目在范围 [1, 2 * 104] 内
1 <= Node.val <= 105
1 <= low <= high <= 105
所有 Node.val 互不相同

方法1:dfs
  • 复杂度：时间复杂度O(n)，空间复杂度O(n)

js:

var rangeSumBST = function(root, low, high) {
    if (!root) {
        return 0;
    }
    if (root.val > high) {
        return rangeSumBST(root.left, low, high);
    }
    if (root.val < low) {
        return rangeSumBST(root.right, low, high);
    }
    return root.val + rangeSumBST(root.left, low, high) + rangeSumBST(root.right, low, high);
};
方法2:bfs
  • 复杂度：时间复杂度O(n)，空间复杂度O(n)

js：

var rangeSumBST = function(root, low, high) {
    let sum = 0;
    const q = [root];
    while (q.length) {
        const node = q.shift();
        if (!node) {
            continue;
        }
        if (node.val > high) {
            q.push(node.left);
        } else if (node.val < low) {
            q.push(node.right);
        } else {
            sum += node.val;
            q.push(node.left);
            q.push(node.right);
        }
    }
    return sum;
};

视频讲解：传送门

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/100600.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

10_缓存-2_二级缓存

10_缓存-2_二级缓存

二级缓存是以namespace为标记的缓存&#xff0c;可以是由一个SqlSessionFactory创建的SqlSession之间共享缓存数据。默认并不开启。下面的代码中创建了两个SqlSession&#xff0c;执行相同的SQL语句&#xff0c;尝试让第二个SqlSession使用第一个SqlSession查询后缓存的数据。要…
阅读更多...
CTF Misc(1)图片隐写基础以及原理，覆盖了大部分题型

CTF Misc(1)图片隐写基础以及原理，覆盖了大部分题型

前言 在ctf比赛中&#xff0c;misc方向是必考的一个方向&#xff0c;其中&#xff0c;图片隐写也是最常见的题目类型&#xff0c;在本篇文章中&#xff0c;将教授以下内容 1.各种图片文件的头数据以及判断是什么类型的图片 2.png图片隐写 3.jpg图片隐写 4.gif图片隐写 5.bmp图…
阅读更多...
Android---RecyclerView实现吸顶效果

Android---RecyclerView实现吸顶效果

目录 一、ItemDecoration 二、实现RecyclerView吸顶效果 1、实现一个简单的RecyclerView。 2、通过ItemDecoration画分割线 3、画出每个分组的组名 4、实现吸顶效果 完整demo 一、ItemDecoration ItemDecoration 允许应用给具体的 View 添加具体的图画或者 layout 的偏移…
阅读更多...
论文投稿指南——中文核心期刊推荐（物理学）

论文投稿指南——中文核心期刊推荐（物理学）

【前言】 &#x1f680; 想发论文怎么办&#xff1f;手把手教你论文如何投稿&#xff01;那么&#xff0c;首先要搞懂投稿目标——论文期刊 &#x1f384; 在期刊论文的分布中&#xff0c;存在一种普遍现象&#xff1a;即对于某一特定的学科或专业来说&#xff0c;少数期刊所含…
阅读更多...
[附源码]计算机毕业设计Python的高校课程知识库(程序+源码+LW文档)

[附源码]计算机毕业设计Python的高校课程知识库(程序+源码+LW文档)

该项目含有源码、文档、程序、数据库、配套开发软件、软件安装教程 项目运行 环境配置&#xff1a; Pychram社区版 python3.7.7 Mysql5.7 HBuilderXlist pipNavicat11Djangonodejs。 项目技术&#xff1a; django python Vue 等等组成&#xff0c;B/S模式 pychram管理等…
阅读更多...
如何做好源代码防泄密

如何做好源代码防泄密

​ 一、前言 • 各类嵌入式研发及平台软件研发行业&#xff0c;都有自己的核心数据以及核心文档&#xff0c;用户数据等敏感信息&#xff0c;这些信息数据有以下共性&#xff1a; –属于核心机密资料&#xff0c;万一泄密会给造成恶劣影响 –核心数据类型多&#xff0c;有…
阅读更多...
验证码是自动化的天敌？看看大神是怎么解决的

验证码是自动化的天敌？看看大神是怎么解决的

01 验证码 1、什么是验证码&#xff1a; 指一种随机生成的信息&#xff08;数字、字母、汉字、图片、算术题&#xff09;等为了防止恶意的请求行为&#xff0c;增加应用的安全性 自动化过程中也是需要进行注册或者登陆的操作&#xff0c;所以需要处理验证 2、验证码处理方式…
阅读更多...
《第一堂棒球课》:MLB棒球创造营·棒球名人堂

《第一堂棒球课》:MLB棒球创造营·棒球名人堂

铃木一朗&#xff0c;1973年10月22日出生于西春日井郡丰山町&#xff08;日本&#xff09;&#xff0c;日本职业棒球运动员&#xff0c;效力于美国职棒大联盟西雅图水手队。 1991年被欧力士蓝浪以第四指名选中&#xff0c;1994年以片假名&#xff08;Ichiro&#xff09;在一军…
阅读更多...
记录一次并发问题的解决

记录一次并发问题的解决

并发问题的产生背景 该问题是在生产运行的过程中出现的。这个运行的项目是一个拉取第三方数据的一个服务&#xff0c;该服务会在拉取到数据之后直接将该数据直接插入到本地库&#xff0c;其中插入本地库的操作是调用的一个静态方法&#xff0c;静态方法对数据进行了多次数据处…
阅读更多...
携程Apollo配置中心架构介绍

携程Apollo配置中心架构介绍

俗话说”麻雀虽小&#xff0c;五脏俱全“&#xff0c;有人说想看开源源码却不知道什么好&#xff0c;事实上&#xff0c;那些流行多年&#xff0c;广受好评的开源工程都是很值得一读的。今天我们介绍Apollo配置中心的基本情况&#xff0c;之所以介绍这个&#xff0c;主要是因为…
阅读更多...
在线地图持续进化，BAT技术“鲜”发制人

在线地图持续进化，BAT技术“鲜”发制人

配图来自Canva可画 眼下&#xff0c;在线地图正在成为智能穿戴、物流运输、旅游度假等诸多领域的“基础设施”&#xff0c;尤其是自动驾驶、车路协同等汽车细分赛道越来越重视在线地图的导入。 得益于此&#xff0c;在线地图市场持续走向火热。华经产业研究院数据显示&#x…
阅读更多...
linux基础学习-ssh基础

linux基础学习-ssh基础

ssh基础 通过SSH客户端我们可以连接到运行了SSH服务器的远程机器上 SSH客户端是一种使用Secure Shell(SSH)协议连接到远程计算机的软件程序目前较为可靠&#xff0c;专门为远程登录会话和其他网络服务提供安全性的协议 利用SSH协议可以有效防止远程管理过程中的信息泄露提供SS…
阅读更多...
行业级开源无人机目标追踪，高空助力抓贼！

行业级开源无人机目标追踪，高空助力抓贼！

活久见&#xff01;成都一高楼惊险无人机抓小偷视频中危险动作&#xff0c;请勿模仿&#xff01; 本次实验中我们使用的是Prometheus 600&#xff08;P600&#xff09;行业级无人机研发平台&#xff08;此平台适用于无人机行业应用开发与室外环境下的无人机算法验证&#xff0…
阅读更多...
White Rose设计与架构的想法分享

White Rose设计与架构的想法分享

在七牛云校园黑客马拉松中&#xff0c;一款设计优秀、逻辑清晰的白板作品脱颖而出&#xff0c;获得第二名的好成绩&#xff0c;这就是来自郑州大学Since团队的White Rose白板&#xff0c;以下是他们的设计和架构分享。 一、前言 White Rose是参加七牛云hackathon比赛的作品&am…
阅读更多...
【】Fate单机部署及代码调试全流程ongoing

【】Fate单机部署及代码调试全流程ongoing

这里写自定义目录标题Fate单机部署及代码调试全流程一、安装Linux系统或者虚拟机-Linux系统1、先装虚拟机2、在虚拟机上安装Ubuntu系统二、FATE单机部署并PyCharm如何连接远程服务器的docker容器进行运行和调试代码【整体未成功&#xff0c;可跳过】三、Ubuntu系统上安装anacon…
阅读更多...
谈谈什么是才是InnoDB解决幻读的最佳方案

谈谈什么是才是InnoDB解决幻读的最佳方案

本文会分享一下MySQL的InnoDB引擎下的事务幻读问题与解决方案--LBCC&MVCC。经过好几天的熬夜通宵&#xff0c;终于把这部分的内容捋清楚了。至于为什么说是InnoDB呢&#xff1f;因为MyISAM引擎是不支持事务的。 事务 概念 一个事情由n个单元组成&#xff0c;这n个单元在…
阅读更多...
Apache 虚拟主机里的 ServerName 指令

Apache 虚拟主机里的 ServerName 指令

术语虚拟主机(Virtual host)是指在一台机器上运行多个网站&#xff08;例如 company1.example.com 和 company2.example.com&#xff09;的做法。 虚拟主机可以是“基于 IP”的&#xff0c;这意味着每个网站都有不同的 IP 地址&#xff0c;也可以是“基于名称的”&#xff0c;…
阅读更多...
Springboot集成Neo4j

Springboot集成Neo4j

一、概述 1.为什么图形数据库&#xff1f; 生活在一个互联的世界中&#xff0c;大多数领域需要处理丰富的连接集以了解真正发生的事情。通常&#xff0c;我们发现项目之间的联系与项目本身一样重要。 虽然现有的关系数据库可以存储这些关系&#xff0c;但它们通过昂贵的JOIN操作…
阅读更多...
微服务框架 SpringCloud微服务架构 服务异步通讯 50 消息可靠性 50.3 消费者消息确认

微服务框架 SpringCloud微服务架构 服务异步通讯 50 消息可靠性 50.3 消费者消息确认

微服务框架 【SpringCloudRabbitMQDockerRedis搜索分布式&#xff0c;系统详解springcloud微服务技术栈课程|黑马程序员Java微服务】 服务异步通讯 文章目录微服务框架服务异步通讯50 消息可靠性50.3 消费者消息确认50.3.1 消费者确认50 消息可靠性 50.3 消费者消息确认 50…
阅读更多...
OTA前装搭载率逼近50%，哪些供应商正在领跑细分赛道

OTA前装搭载率逼近50%，哪些供应商正在领跑细分赛道

智能汽车的OTA&#xff0c;正在进入新发展周期。 早期的OTA&#xff0c;主要围绕座舱信息娱乐、T-BOX及少部分车内其他ECU&#xff0c;主要目的是修复软件Bug以及改进用户体验&#xff0c;降低整车的召回成本。这个阶段&#xff0c;OTA对应的整车电子架构还是以传统的分布式EC…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023