【Java 基础篇】Java TreeSet 详解：红黑树实现的有序集合

在这里插入图片描述

Java 集合框架提供了多种数据结构，用于存储和操作数据。其中，TreeSet 是一种特殊类型的集合，它通过红黑树（Red-Black Tree）数据结构实现了有序的、唯一元素存储。本篇博客将深入探讨 TreeSet，包括其概念、特性、内部实现、使用方法以及示例代码。无论您是初学者还是有一定经验的 Java 开发者，都能在这里找到有关 TreeSet 的有用信息。

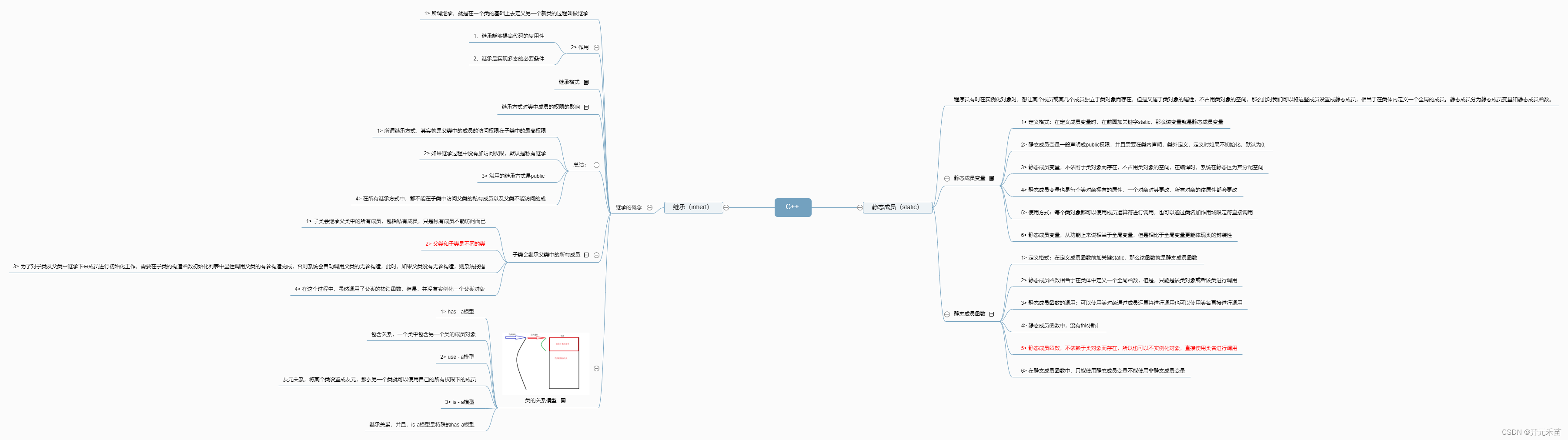
1. 什么是 TreeSet？

1.1. 集合的基本概念

在开始介绍 TreeSet 之前，我们先来回顾一下集合的基本概念。

集合是 Java 编程中常用的数据结构之一，它用于存储一组对象。集合通常分为两大类：

有序集合（Ordered Collection）：其中的元素按照某种顺序排列，可以是添加顺序、自然顺序或自定义顺序。
无序集合（Unordered Collection）：其中的元素没有明确定义的顺序。

集合可以用于存储不同类型的数据，例如整数、字符串、对象等。在使用集合时，我们通常关心以下几个方面的问题：

唯一性：集合是否允许重复元素。
有序性：集合中的元素是否有顺序。
性能：在集合中执行常见操作的性能，如添加、删除、查找等。

1.2. TreeSet 的定义

TreeSet 是 Java 集合框架中的一种有序集合，它实现了 Set 接口，因此具有不允许重复元素的特性。与 HashSet 不同，TreeSet 使用红黑树数据结构来存储元素，这使得元素在集合中保持有序。

这里需要理解两个主要特性：

有序性（Order）：TreeSet 中的元素按照自然排序（元素的自然顺序）或者指定的排序方式（通过比较器）排列。这意味着您可以遍历 TreeSet 得到的元素是按照一定的顺序排列的。
唯一性（Uniqueness）：与 HashSet 一样，TreeSet 也保证元素的唯一性，不允许重复元素。

因此，TreeSet 是一个适用于需要有序存储唯一元素的场景的理想选择。

2. TreeSet 的内部实现

要深入理解 TreeSet，我们需要了解它的内部实现机制，即红黑树。红黑树是一种自平衡二叉搜索树（Self-Balancing Binary Search Tree），它具有以下特性：

每个节点要么是红色，要么是黑色。
根节点是黑色。
每个叶子节点（NIL 节点，空节点）是黑色的。
如果一个节点是红色的，则它的两个子节点都是黑色的。
从任意节点到其每个叶子节点的所有路径都包含相同数目的黑色节点。

这些规则确保了树的平衡，从而保证了树的高度不会过高，使得查找、插入和删除操作的性能稳定。

在 TreeSet 中，元素被存储在红黑树的节点中，根据元素的大小关系构建树结构。这意味着，插入、删除和查找操作的时间复杂度为 O(log n)，其中 n 是集合中的元素个数。由于红黑树的平衡性质，这些操作的性能是可预测的。

3. TreeSet 的创建与初始化

要使用 TreeSet，首先需要创建和初始化它。以下是一些常见的初始化方法：

3.1. 默认构造函数

使用默认构造函数创建一个空的 TreeSet 对象：

TreeSet<String> treeSet = new TreeSet<>();

这将创建一个初始容量为 16 的 TreeSet，加载因子为 0.75。您可以根据需要调整这些参数。

3.2. 指定排序方式的构造函数

您可以使用带有 Comparator 参数的构造函数来指定元素的排序方式。比如，创建一个降序排列的 TreeSet：

TreeSet<Integer> customOrderTreeSet = new TreeSet<>(Comparator.reverseOrder());

3.3. 从现有集合创建

您还可以从现有的集合（如 List 或 Set）创建一个 TreeSet，以便在不同集合类型之间进行转换：

Set<String> existingSet = new HashSet<>(Arrays.asList("A", "B", "C"));
TreeSet<String> treeSetFromSet = new TreeSet<>(existingSet);

这将使用现有集合中的元素来初始化新的 TreeSet。

4. 基本操作：添加、删除和查询元素

TreeSet 提供了常见的集合操作，包括添加、删除和查询元素。以下是一些基本操作的示例：

4.1. 添加元素

使用 add 方法来向 TreeSet 中添加元素：

treeSet.add("D");
treeSet.add("E");

4.2. 删除元素

使用 remove 方法来从 TreeSet 中删除元素：

treeSet.remove("B");

4.3. 查询元素是否存在

使用 contains 方法来检查元素是否存在于 TreeSet 中：

boolean containsC = treeSet.contains("C");

5. 遍历 TreeSet

遍历 TreeSet 中的元素通常使用迭代器或增强的 for 循环。以下是两种遍历方式的示例：

5.1. 使用迭代器遍历

Iterator<String> iterator = treeSet.iterator();
while (iterator.hasNext()) {
    String element = iterator.next();
    System.out.println(element);
}

5.2. 使用增强的 for 循环遍历

for (String element : treeSet) {
    System.out.println(element);
}

无论哪种方式，遍历 TreeSet 都会按照元素的顺序输出元素值。

6. 示例：使用 TreeSet

让我们通过一些示例代码来演示 TreeSet 的使用场景：

6.1. 存储成绩

假设我们要存储一组学生的成绩，并且希望按照成绩从低到高的顺序排列。我们可以使用 TreeSet 来实现：

TreeSet<Integer> studentScores = new TreeSet<>();

studentScores.add(85);
studentScores.add(92);
studentScores.add(78);
studentScores.add(92); // 这个重复的成绩将被忽略

for (int score : studentScores) {
    System.out.println("成绩：" + score);
}

输出：

成绩：78
成绩：85
成绩：92

6.2. 记录考试排名

假设我们要记录一场考试的排名，并希望排名按照分数从高到低的顺序排列。我们可以使用 TreeSet 来存储排名信息：

TreeSet<Ranking> examRankings = new TreeSet<>(Comparator.reverseOrder());

examRankings.add(new Ranking("Alice", 95));
examRankings.add(new Ranking("Bob", 88));
examRankings.add(new Ranking("Charlie", 92));

for (Ranking ranking : examRankings) {
    System.out.println("排名：" + ranking.getName() + "，分数：" + ranking.getScore());
}

输出：

排名：Alice，分数：95
排名：Charlie，分数：92
排名：Bob，分数：88

7. TreeSet 的更多用法

当使用 TreeSet 时，除了基本的添加、删除、查询和遍历操作，还可以利用其更多的特性和方法来满足不同的需求。接下来，我们将介绍一些 TreeSet 的更多用法。

7.1. 获取第一个和最后一个元素

如果您需要获取 TreeSet 中的最小元素（第一个元素）或最大元素（最后一个元素），可以使用以下方法：

String firstElement = treeSet.first(); // 获取第一个元素
String lastElement = treeSet.last(); // 获取最后一个元素

这些方法在需要找到极值元素时非常有用。

7.2. 获取小于或大于某个元素的子集

TreeSet 提供了 headSet 和 tailSet 方法，用于获取小于或大于某个元素的子集。这在需要根据某个元素的值来划分集合时非常有用。

TreeSet<Integer> numbers = new TreeSet<>(Arrays.asList(1, 2, 3, 4, 5, 6, 7, 8, 9));

// 获取小于等于 5 的子集
SortedSet<Integer> lessThanOrEqualFive = numbers.headSet(5); // [1, 2, 3, 4, 5]

// 获取大于等于 5 的子集
SortedSet<Integer> greaterThanOrEqualFive = numbers.tailSet(5); // [5, 6, 7, 8, 9]

7.3. 获取某一范围内的子集

除了获取小于或大于某个元素的子集，还可以获取某一范围内的子集，使用 subSet 方法：

// 获取范围在 [3, 7) 之间的子集（不包含 7）
SortedSet<Integer> subset = numbers.subSet(3, 7); // [3, 4, 5, 6]

7.4. 寻找最接近的元素

TreeSet 提供了 ceiling 和 floor 方法，用于寻找最接近指定元素的元素。ceiling 方法返回大于等于指定元素的最小元素，而 floor 方法返回小于等于指定元素的最大元素。

TreeSet<Integer> numbers = new TreeSet<>(Arrays.asList(1, 3, 6, 8, 10));

int closestGreaterOrEqual = numbers.ceiling(5); // 返回 6
int closestLessOrEqual = numbers.floor(5); // 返回 3

7.5. 比较两个 TreeSet

如果您需要比较两个 TreeSet 是否相等或一个是否包含另一个，可以使用 equals 和 containsAll 方法：

TreeSet<Integer> set1 = new TreeSet<>(Arrays.asList(1, 2, 3, 4, 5));
TreeSet<Integer> set2 = new TreeSet<>(Arrays.asList(3, 4, 5));

boolean areEqual = set1.equals(set2); // 判断两个集合是否相等
boolean containsAll = set1.containsAll(set2); // 判断 set1 是否包含 set2 的所有元素

7.6. 自定义比较器

默认情况下，TreeSet 使用元素的自然顺序来排序。但是，您也可以通过提供自定义比较器来指定排序规则。比较器必须实现 Comparator 接口。

// 使用自定义比较器来按字符串长度排序
TreeSet<String> customOrderSet = new TreeSet<>(Comparator.comparing(String::length));

customOrderSet.add("apple");
customOrderSet.add("banana");
customOrderSet.add("cherry");

// 结果：[apple, cherry, banana]

以上是 TreeSet 的一些更多用法，根据您的需求，您可以灵活运用这些方法来处理和操作有序集合中的数据。请根据具体场景选择适当的方法和特性，以便更高效地使用 TreeSet。

8. TreeSet 使用注意事项

在使用 TreeSet 时，有一些注意事项需要考虑，以确保正确、高效地使用该集合。

8.1. 唯一性

TreeSet 是一个有序的集合，它确保了元素的唯一性。这意味着集合中不会包含重复的元素。如果您尝试将重复元素添加到 TreeSet 中，它们将被忽略。因此，如果您需要处理重复元素，可能需要考虑其他集合类型，如 ArrayList 或 LinkedList。

8.2. 自然顺序

TreeSet 默认按照元素的自然顺序进行排序。如果元素类型实现了 Comparable 接口，它将使用 compareTo 方法来确定元素之间的顺序。如果元素类型没有实现 Comparable 接口，并且没有提供自定义的比较器，添加元素时可能会引发 ClassCastException。

8.3. 自定义比较器

如果需要根据不同的排序规则来处理元素，可以提供自定义的比较器。自定义比较器必须实现 Comparator 接口，并在创建 TreeSet 时传递给构造函数。这样，您可以控制元素的排序方式，而不仅仅依赖于自然顺序。

8.4. 性能考虑

TreeSet 的插入、删除和查询操作的平均时间复杂度为 O(log n)，其中 n 是集合中的元素数量。这意味着 TreeSet 对于大型数据集合是高效的。然而，在某些情况下，其他数据结构，如 HashSet，可能会更快，因为它们的性能更接近于 O(1)。

8.5. 并发性

TreeSet 不是线程安全的，如果多个线程同时访问和修改同一个 TreeSet 实例，可能会导致不一致的结果或并发问题。如果需要在多线程环境中使用 TreeSet，请考虑使用 Collections.synchronizedSortedSet 来创建一个线程安全的集合。

8.6. 遍历顺序

TreeSet 的元素是按照排序顺序存储的。因此，通过迭代器或增强的 for 循环遍历时，元素的顺序是有序的。这可以用于按顺序访问元素，但请注意，这可能与元素插入的顺序不同。

8.7. 空集合

TreeSet 可以包含空元素（null），但请小心使用。如果您要在集合中包含 null 元素，请确保您的比较器或元素类型不会导致意外的行为。

总之，TreeSet 是一个强大的有序集合，但在使用时需要注意其唯一性、排序方式、性能、并发性等方面的问题。根据具体需求选择合适的集合类型，并确保正确处理和操作数据以避免潜在的问题。

9. 总结

在本篇博客中，我们深入探讨了 TreeSet，这是 Java 集合框架中的一种有序集合。我们了解了它的概念、特性、内部实现、创建与初始化方法以及基本操作。通过示例代码，我们演示了如何使用 TreeSet 来解决不同场景的问题，如存储成绩和记录考试排名。希望本文能帮助您更好地理解和应用 TreeSet，并在实际开发中充分利用它的有序性和唯一性特点。如果您有任何问题或建议，请随时提出，我们将竭诚为您提供帮助。