引言

 目标

        傅里叶变化（Fourier transform）是一种信号处理技术，它可以将时间信号转换为频率信号，即将一组具有相同数量频率的正弦波叠加在一起，形成一组新的正弦波。如果我们把时间信号从频域转换到时域，那么就会得到一个“频谱”。所以傅里叶变化就是通过分析不同频率正弦波的相位差，来确定它们的频率。 傅里叶变化在信号处理中有广泛应用。比如，可以用它来检测和定位信号中的突变点；可以用它来确定信号中是否存在非周期信号；可以用它来分析复杂系统的行为；还可以用它来计算复杂系统的频谱等。 那么我们为什么要使用傅里叶变化呢？

 意义

        如果你是一个对音乐敏感的人，那么你一定会发现，我们今天讨论的这个主题似乎非常熟悉。在任何技术领域，几乎都能找到类似的事情：从音频和视频的分析中发现信号中的非周期性成分。当然，这种分析是复杂的，有时甚至是不可能的，因为在现实世界中，这些信号可能是由许多不同的原因产生的。但是，它们通常都会以特定的方式出现。这就是为什么我们要使用傅里叶变化。 傅里叶变化在技术分析中有很多用途。它可以帮助我们确定信号是否包含一些频率之外的频率成分。或者，如果我们想找出特定信号或噪声的频率范围，我们可以使用傅里叶变化来确定它是否会出现在我们要找的范围内。 如果你还不知道如何使用傅里叶变化，那么这篇博文可以帮您非常深入的了解。

背景知识

  声音

        我们知道声音是一种机械波，是由振动产生的。我们生活的世界就是由各种不同频率、不同振幅、不同方向的振动组成的。通常把频率范围为20Hz-20kHz的振动称为声音；频率范围为1 kHz-20 kHz的振动称为乐音；频率范围为2 kHz-20 kHz的振动称为声音；频率范围为3 kHz-20 kHz的振动称为高音。另外，还存在有某些频率范围在10-6~10-7 Hz之间（如人耳可听到的次声波）的声音。可以说，每个人都能发出声音，但发出什么样的声音取决于振动器官所处环境和声波频率。但是声音究竟是什么样子的呢？？？我们使用一种特殊的拍照可以查看声波穿过空气分子时看到空气分子的运动，如图1.1。这是Michael Hargather 博士和 Gary Settles 博士进行的一项实验，他们在纹影装置内的摄像头前放置了一个发出单一音调的扬声器。并拍摄了周围空气分子发生的情况。中间红色的椭圆是扬声器通过空气远离它的是声波，当空气分子聚在一起时会得到一个波峰显示出一个高压区 ，当空气分子再次被拉开时会看到一个低气压区域的形成。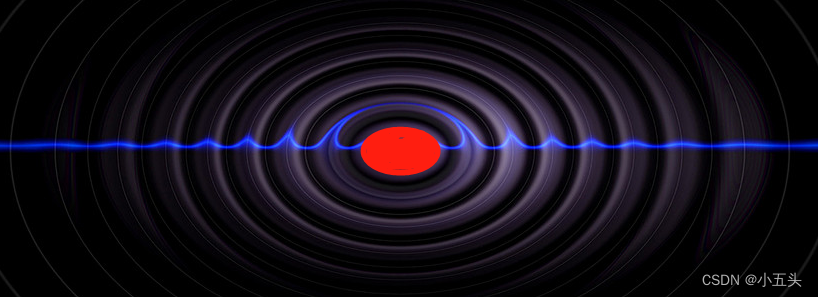

图1.1

        当在扬声器面前放置一个假球时，可假想球经过声波的震动如何上下摆动的如图1.2。一直持续下去我们可以绘制出声音波形的表示。而我们在数学上有一个函数就可以表示此波形SIN函数。

图1.2

        如果在三角形上取①点的正弦值并将其乘以斜边的长度就可以计算出三角形定点的高度如图1.3。

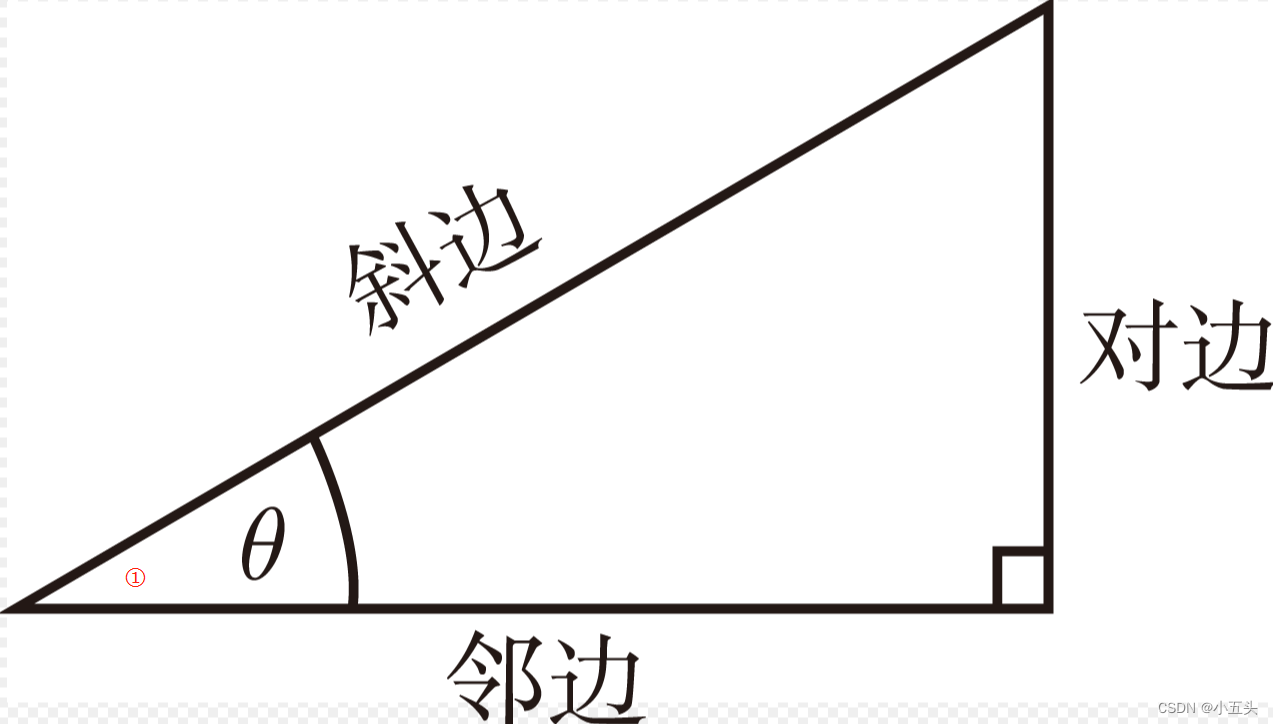
图1.3

        随着我们三角形的角度增加，它会绕着旋转三角形的顶点成为一个圆圈，如果把它对应在二维坐标系中，三角形旋转的不同角度的形状看起来与之前的声波信号非常相似图1.4。这就是为什么sin信号是声音一个很好的近似值。但如果只是单纯的一个正弦波那么听起来就是一种很刺耳的声音如果想让正弦波听起来想现实生活中听到的声音呢？

图1.4

        稍微以不同的方式看待声波信号的波浪，假设正弦波的基本形状永久保持不变，它总是随着时间的推移上升和下降的。那么我们可以改变正弦波的那个属性（频率、幅度、相位），先从频率改变缩短正弦波或者拉长正弦波，幅度可以拉高正弦波或拉低正弦波。最终所呈现的声音也会随之发生改变。如图1.5表示的是在时域下查看幅度与频率的关系。如图1.6所表示的是在频域下查看幅度与频率的关系。

图1.5

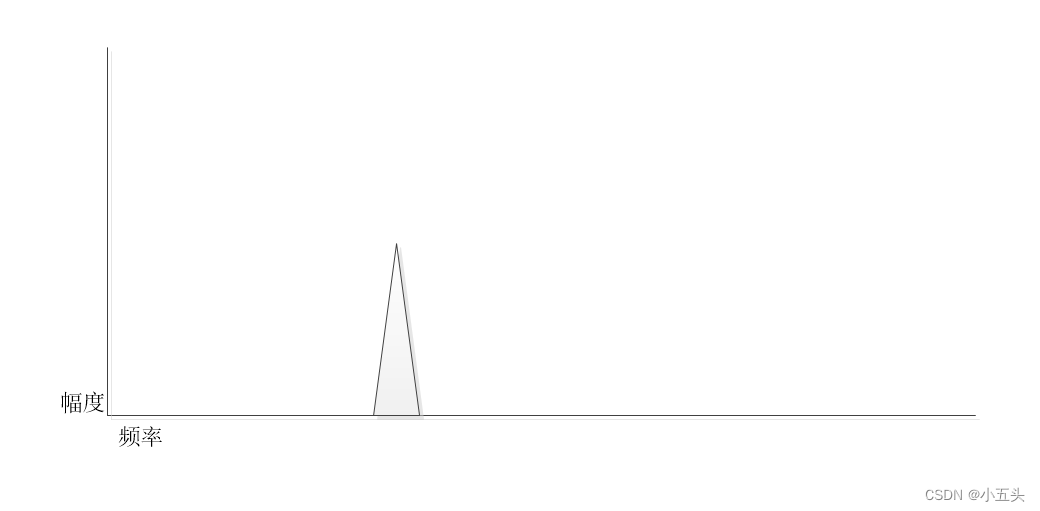
图1.6

        而多频率信号叠加在一起时候的时域下如图1.7。频域下查看如图1.8.

图1.7

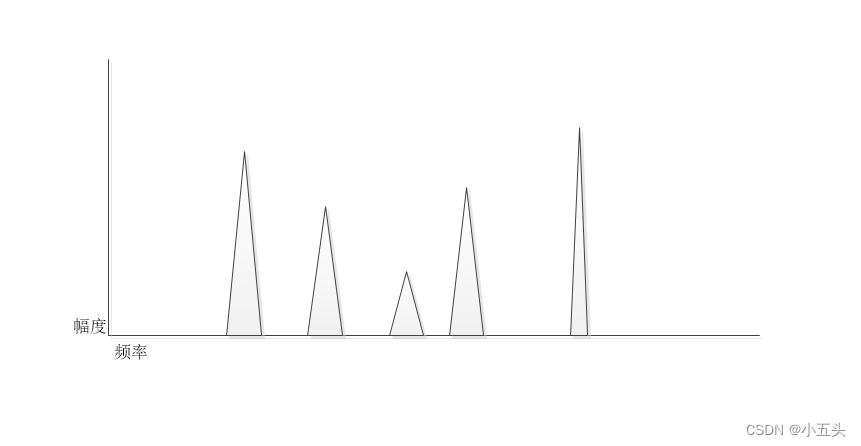
图1.8

          显示世界中发出的声音，实际是不同频率和振幅的正弦波，这一系列的正弦波加在一起就是所谓的傅里叶系列。

 相位

        取一个频率为440Hz的正弦波与一个频率为660Hz的正弦波，将二者叠加在一起，然后开始改变660Hz的相位，相加后的波形会随着第二个波形的相位改变而发生变化。因此如果想要使用傅里叶级数准确的表示该信号为一系列正弦波，那么每个波的相位信息也很重要，因为它会印象信号的整体形状，那么如果在数学上表示这种相移呢如图1.9。傅里叶曾经说过一个变量的任何函数都可以在该变量的倍数的一系列正弦中展开。当我们谈论声音信号时，我们的变量在X轴上发生是时间，而在当时傅里叶提出他的理论时，他正在测量热流所以他的变量很可能是距离，因此需要一些可以应用于所有类型信号的通用变量。在谈论正弦波时角度是常见的变量然后可以缩短此变量，以用于我们正在处理的任何信号。如果我们有一个频率为660Hz的声波，这意味着我们耳朵周围的空气，正在以每秒660Hz的速度被压缩和膨胀。意味着1个压缩/扩展周期所需的时间是1/660秒。

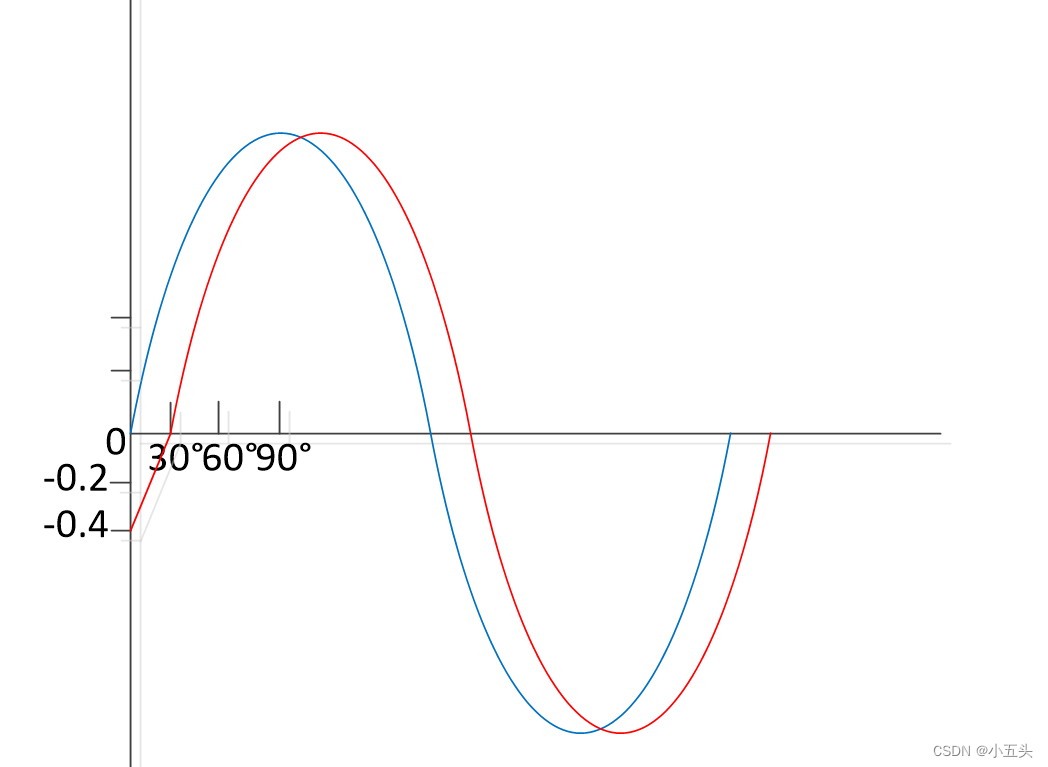
图1.9

        完成一个正弦波的一个周期需要360°也就是在园内旋转一周如图2.0。因此我们可以将声音信号的一个周期所花费的时间映射到360°是圆上，因此如果我们想将信号相移30°，则30°是360°的12度（正弦波的一个周期），因此对于需要1/660秒完成的一个周期的660Hz信号，1/660秒的12秒=0.000126秒如图2.1.

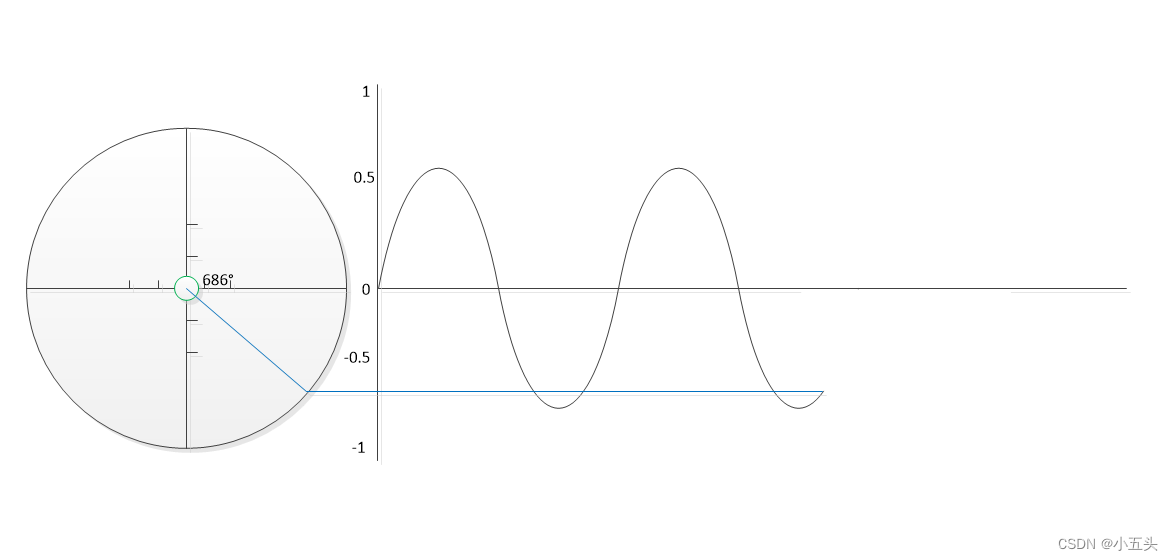
图2.0

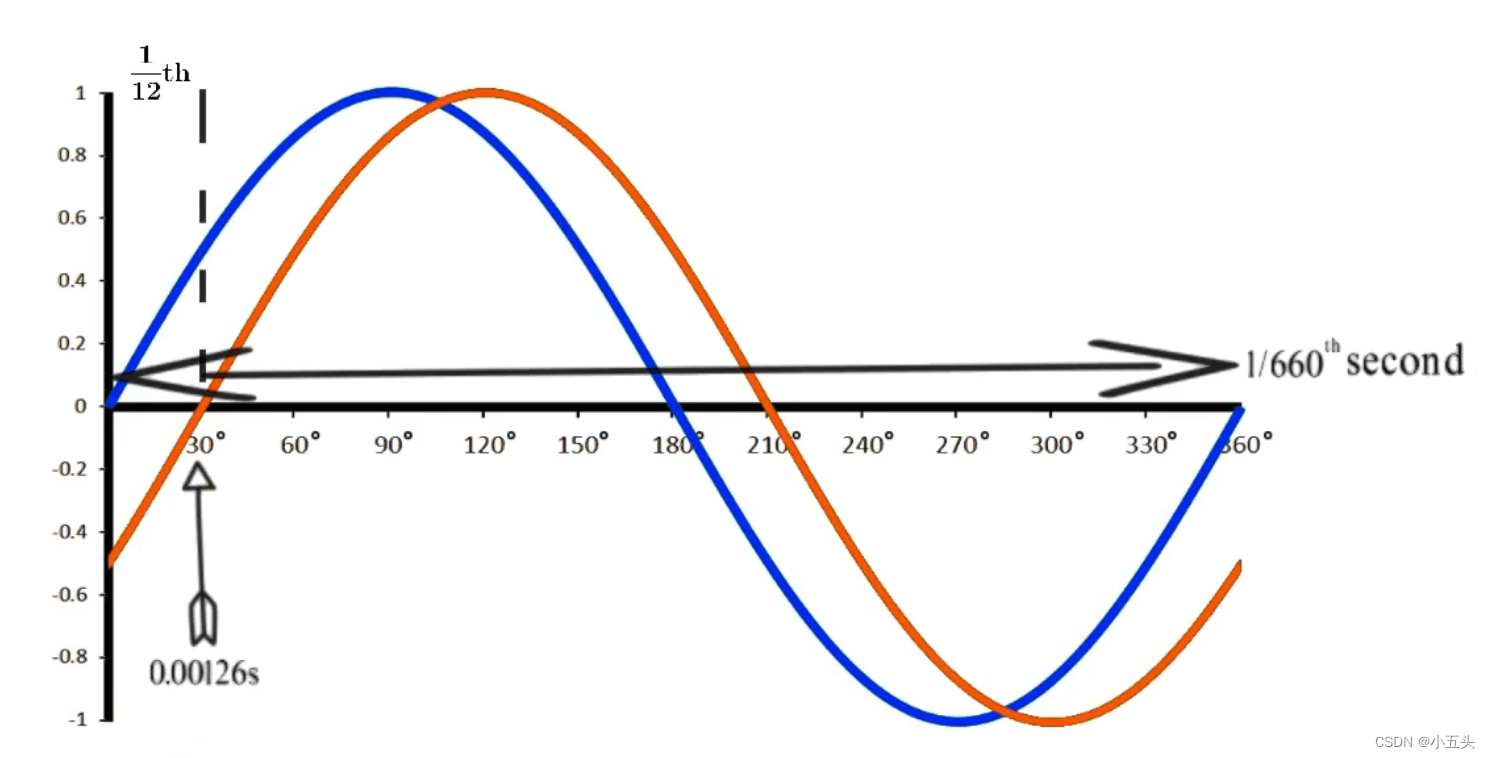
图2.1

        因此要将正弦波的角度变量转换，为信号的时间变量，我们将角度除以360°并乘以周期信号，在本例中为1/660秒。需记住乘以信号周期等于除以频率。频率是每秒的信号周期数660Hz表示每秒660个完整的正弦波周期。如果我们将信号的时间变量转换，为正弦波的角度变量，而在这种情况下我们除以信号周期并乘以360°或者，因为这次我们除以周期，我们可以简单的乘以频率。因此要将时间转换为角度，我们乘以频率然后乘以360°。

        所以我们在数学上表示30°的相移！注意看第二个正弦波比第一个正弦波滞后30°如图2.2。如果角度为30°蓝色正弦波的幅度为0.5，红色正弦波不会达到0.5。当角度为60°，再达到30°。因此红色波的方程：SIN（X-30°）。

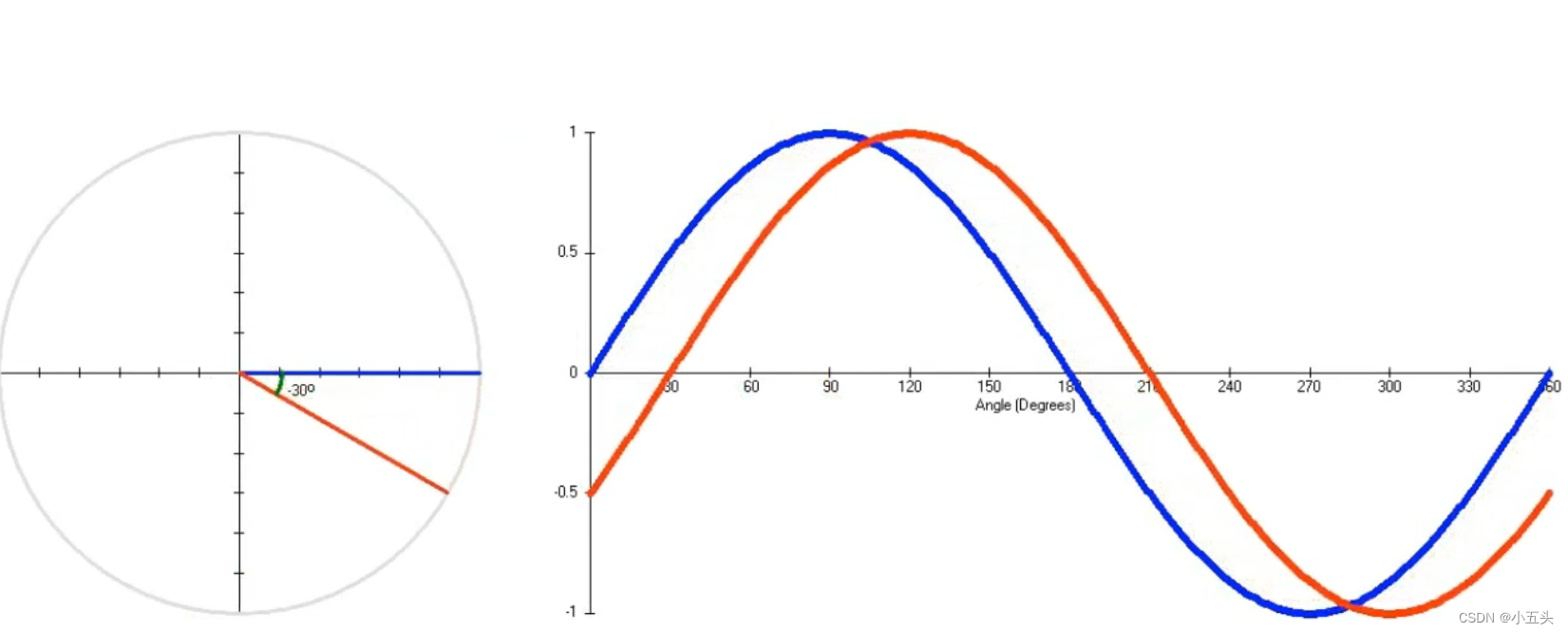
图2.2

        如果我们将红波移向另一个方向，使红波领先与蓝波30°。而红波现在的方程为：SIN（X+30°）如图2.3。

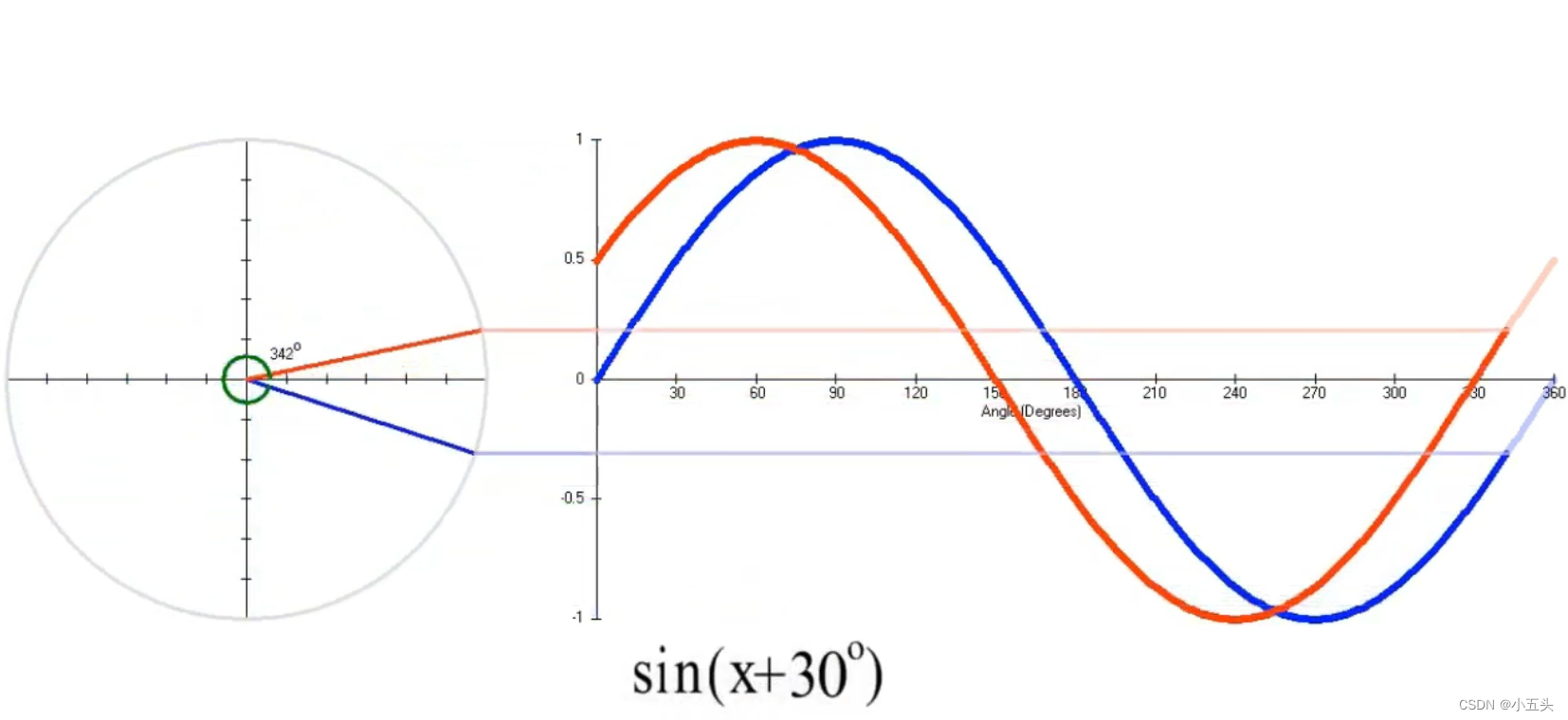
图2.3

        如果我们将正弦波移动90°，会得到另一个三角函数（余弦函数）描述的波。所以SIN（x+90°）= COS（X）。

        如图2.4所示.如果我们取这个角的正弦值，乘以斜边的长度，可以计算出三角形的高度。取角度的余弦值并乘以斜边长度，可以计算出三角的宽度。

图2.4

        如果我们将三角形旋转90°，三角的宽度现在变成了它的高度。所以任何角的正弦，称为sin(X+90°) 等于 该角的余弦值。所以到目前为止有两种方法可以查看正弦和余弦函数的办法。要么相位可以改变的波，要么是角度可以改变的三角形。

        当我们查看旋转三角形时，看到这个角度对于改变正弦波相位的量。我们可以通过两个不同的波（余弦波和正弦波）相加来描述任何相移相同的频率，只需某种方法改变它们的振幅。如图2.5

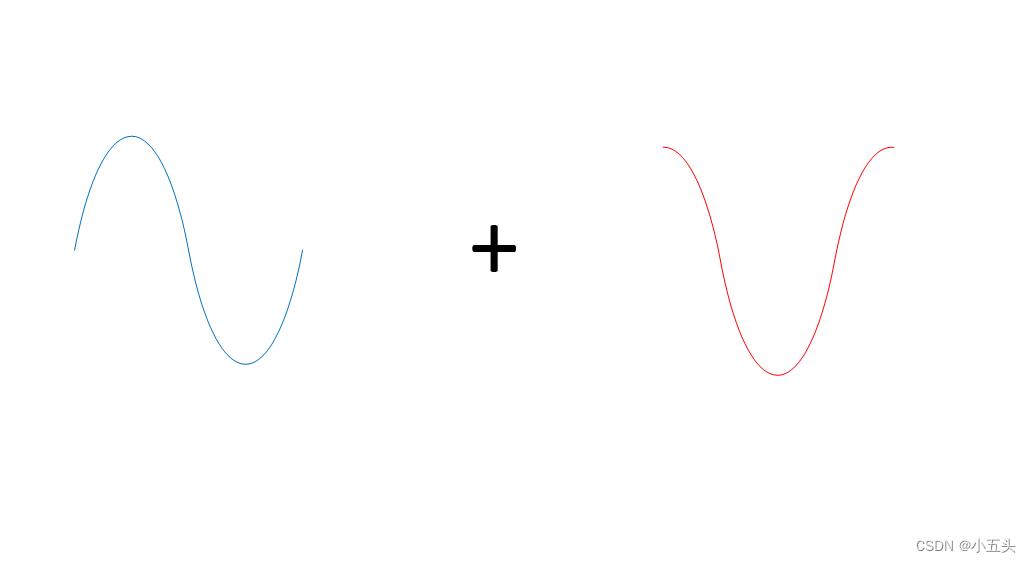
图2.5

        我们将从振幅为32的余弦开始如图2.6，可以看到这只是一个没有相移的普通的余弦波。还有一个振幅位29的正弦波同样是一个没有相移的普通正弦波。

图2.6

        将两个波形进行相加如图2.7。这是一个大约偏移42°的余弦波，如果想知道它的振幅是多少，首先回到三角形建模。如图2.8。余弦波为32幅度由三角形底边长表示，正弦波为29幅度由三角形高长度表示。那么斜边的长度需要用到勾股定理求出：斜边上的平方等于其他两条边上的平方和。而这就是相移后的波形幅度值。

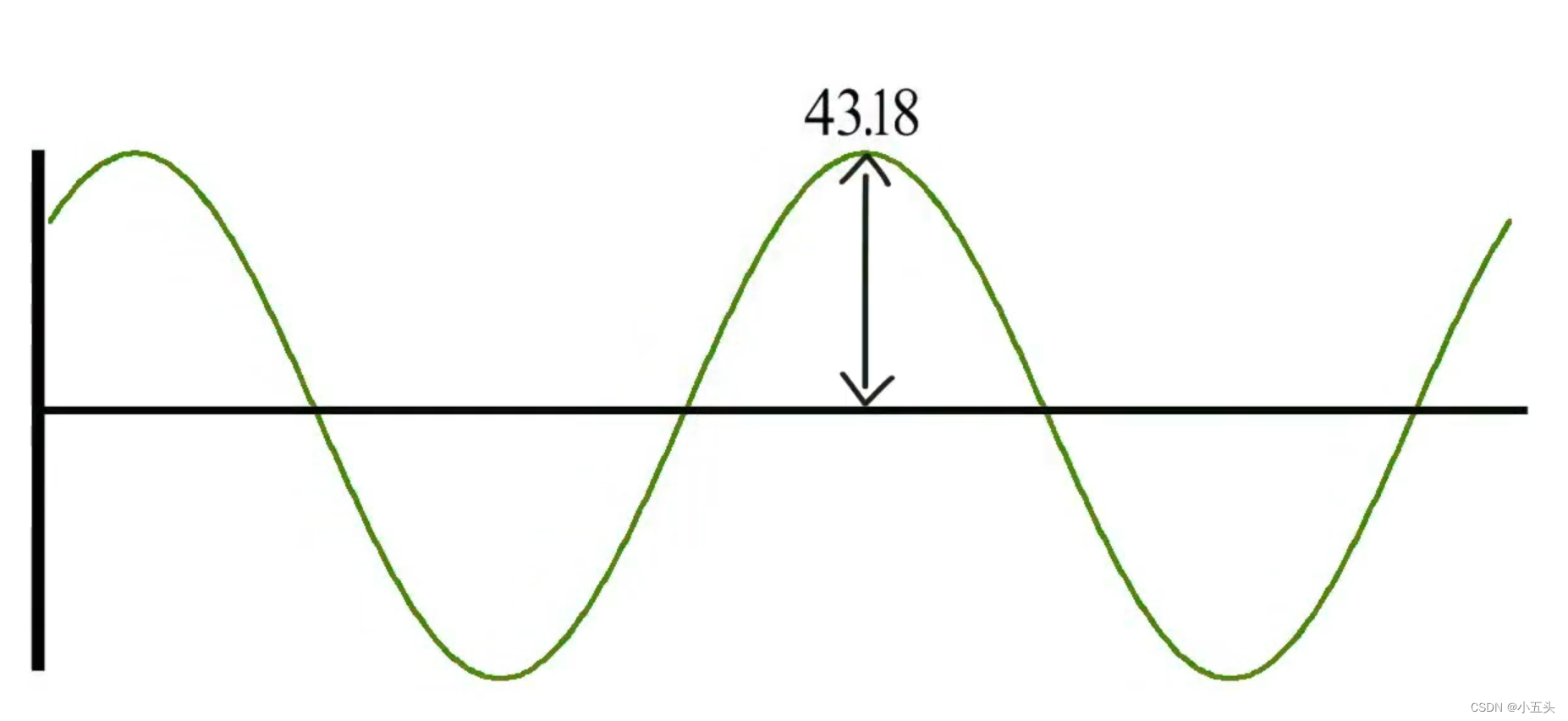
图2.7

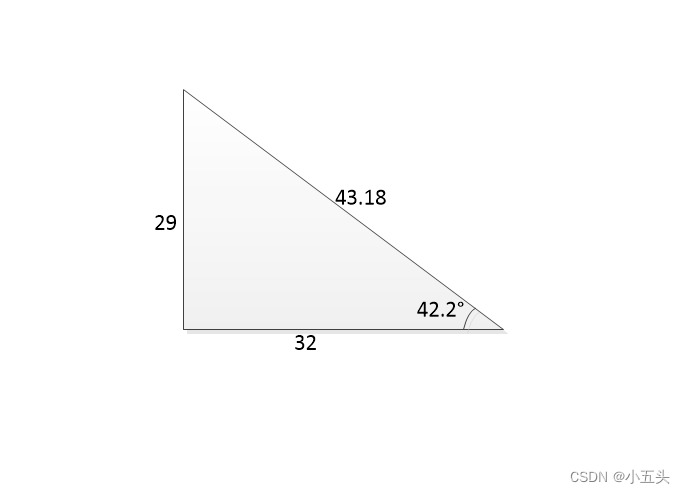
图2.8

        根据余弦波与正弦波的幅度计算角度？在一次把波形看作成三角形。如果增加三角形的宽度而高度保持不变，角度会缩小。如果增加三角形的高度但宽度保持不变，角度会增加。如果增加三角的宽度，那么为了保持角度不变，就必须增加它的高度。这意味着三角的角度、高度和宽度之间必须存在关系。保持三角形的宽度相同，并增加高度会使角度一起增加。随着除法运算的分子增加，除法结果也会增加如图2.9，就像三角形的角度一样，所以高度必须构成除法的分子。保持三角形的高度相同，并增加宽度会使角度缩小。随着除法运算分母的增长，除法结果会缩小如图3.0就像三角形的角度一样，因此宽度必须构成除法的分母。

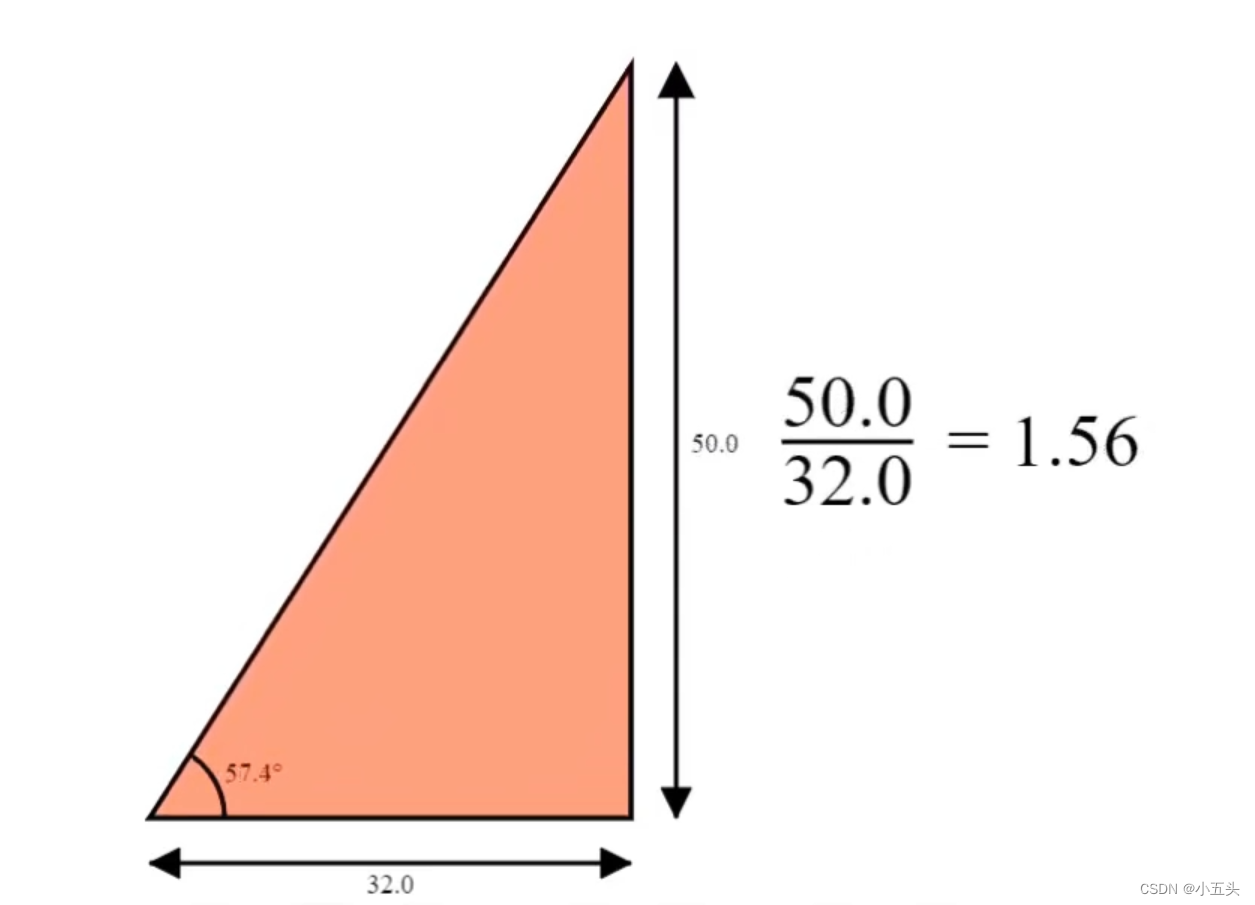图2.9

图3.0

        在图形的X轴上绘制，三角形的高度除以宽度的结果，要测量三角形的角度，并将其绘制在Y轴上如图3.1。可以清晰的看到三角形的宽度，高度和角度之间存在的关系，但它不是直接甚至线性关系。也就是说高度除以宽度还不足以给出角度，如果只知道三角形的的宽度和高度，还需要进行其他操作才能恢复三角形的角度。

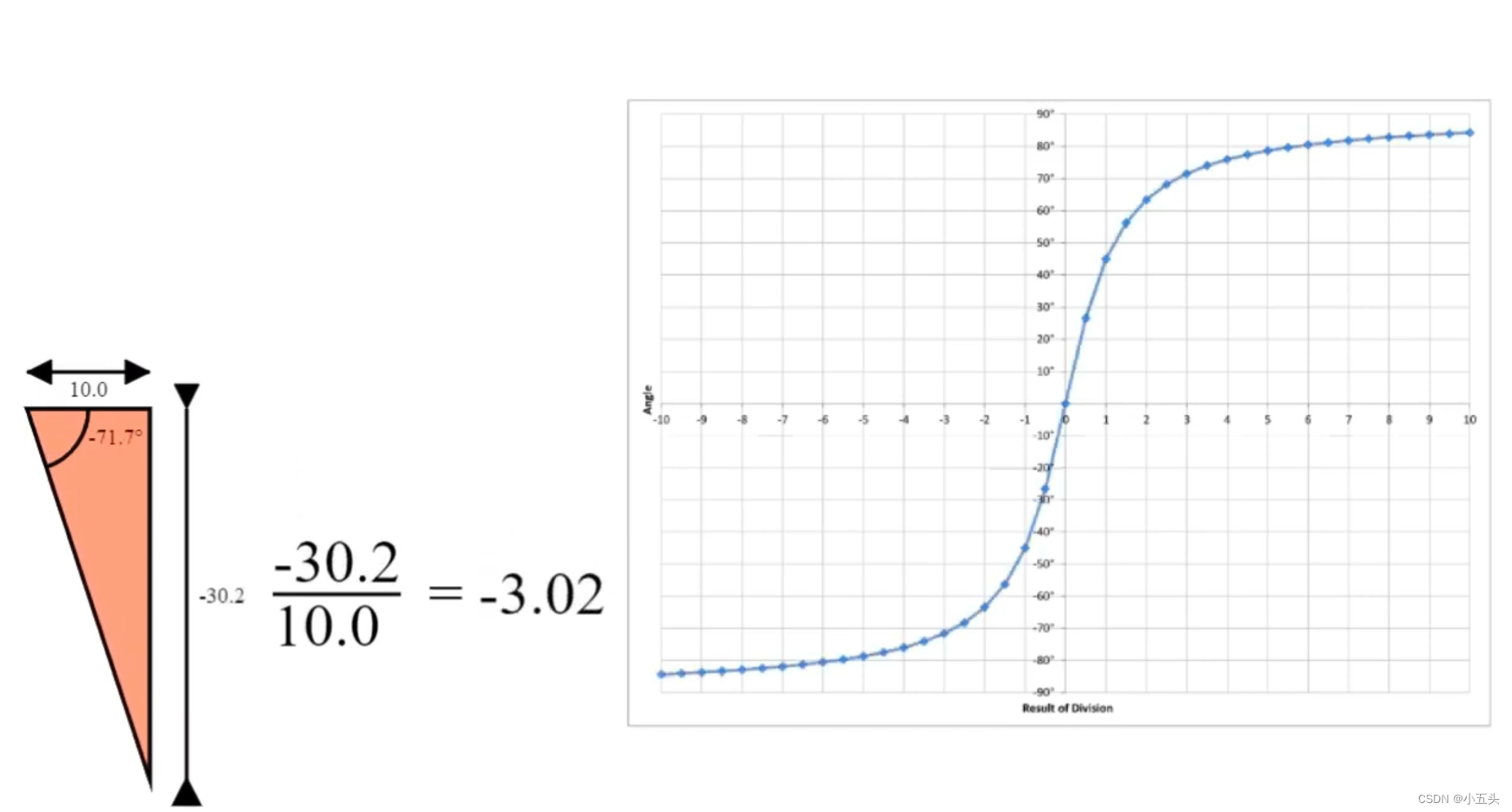
图3.1

        为了计算三角形的高度，我们将斜边乘以角度正弦。计算三角形的宽度，将斜边乘以角的余弦。通过这俩个表达式来恢复角度。斜边乘以角的正弦除以斜边乘以角的余弦。经过化简又得到一个正切函数。所以恢复角度的公式为：高度/宽度的反正切如图3.2所示。

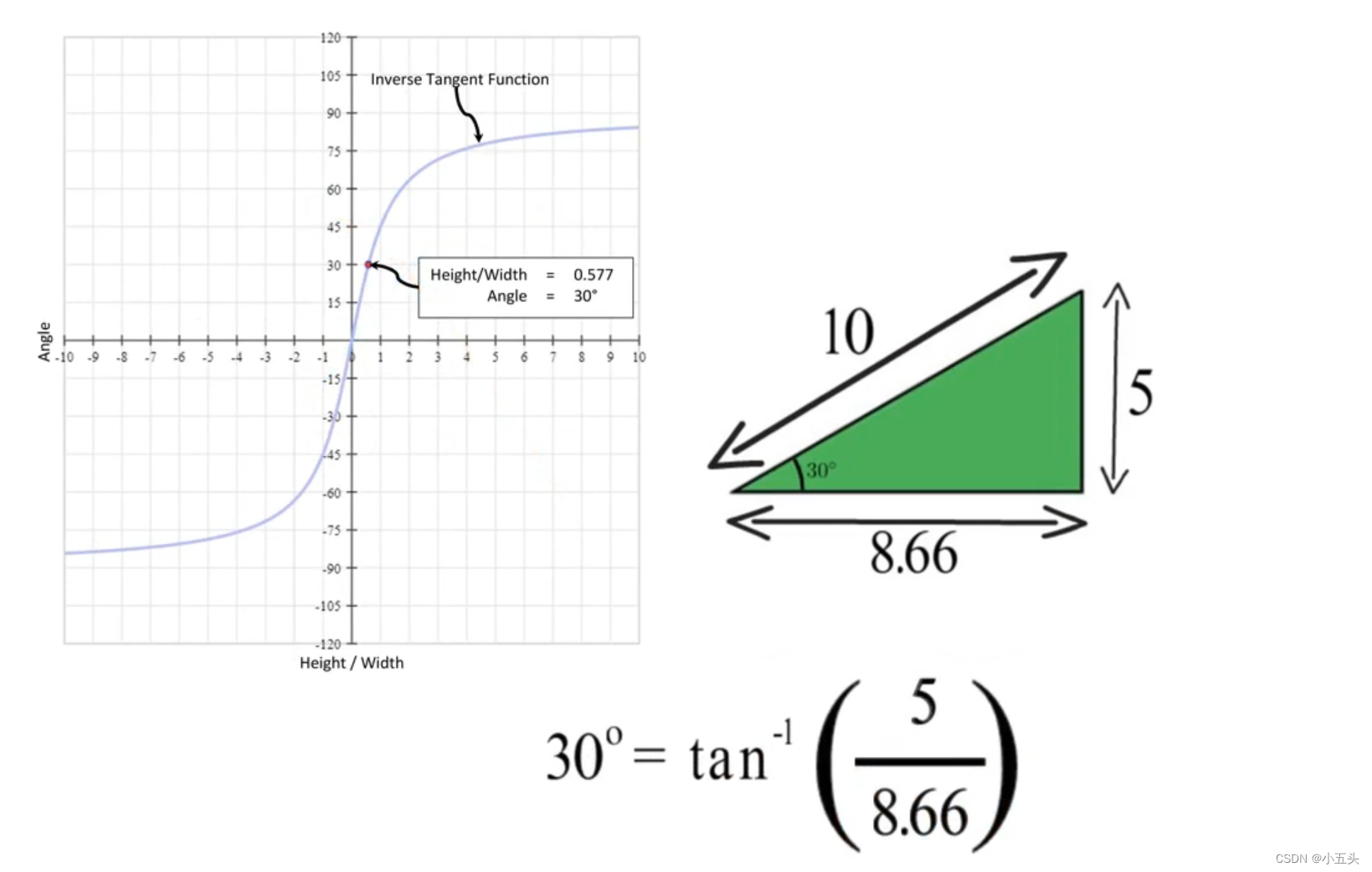
图3.2

        通过上述例子中，正弦波幅度为29余弦波幅度32，角度计算后得出结果42°。因此通过将频率相同但是幅度不同的正弦波和余弦波相加，可以改变合成波的相位。

        众所周知一个圆圈是360°，然而还有一种角度测量方法，使用弧度。一个弧度的定义是这三个长度都相等的角度如图3.3所示。因此如果圆的半径为1，那么角度在一弧度时，该弧度的长度也将为1。如果将角度增加到2弧度，那么求得弧长需要知道圆弧的长度总是等于半径乘以弧度角。所以在单位圆上，就是一个半径为1的圆，弧长为2就像弧度角一样。我们知道圆的周长等于π=3.1415926。如果弧度角等于圆弧的长度，那么在一个圆上一定有2π弧度。

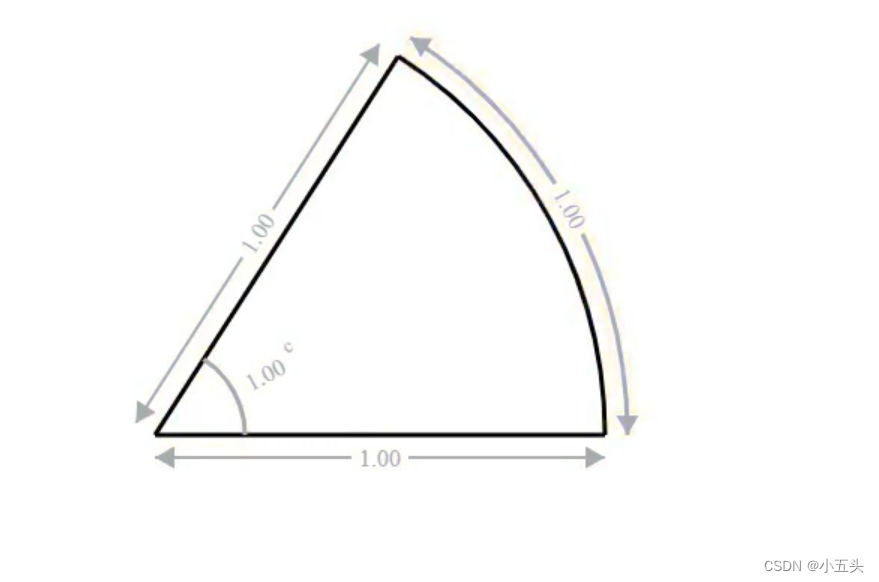
图3.3

 欧拉公式

        著名的美国物理学家理查德·费曼，研发出一项特别的公式，他称之为“我们的宝石”和“数学中最杰出的公式”。他所指就是如图3.4所示。是菜昂哈德·欧拉于1748年首次表达的欧拉身份。昂哈德·欧拉 于1707年4月15日出生瑞士巴塞尔。英国数学家，数学家、天文学家、物理学家、力学和天体力学的奠基人之一。欧拉对数学物理做出了许多重大的贡献，被公认为是十七世纪最伟大的数学家。欧拉在数学、几何学、代数学、力学和天文学等方面都有很深的造诣，为近代科学奠定了坚实的基础。他提出了“连续统假设”，证明了欧拉数，创立了“复变函数论”。欧拉对数学物理的贡献有许多是后人难以企及的，他被称为“数学王子”。

图3.4

        雅各布·佰努利发现，如果他在年初存入1美元，并在当年给自己共100%的利息，那么无论他全年分摊多少利息，他都无法超过总计到年底为2.72美元。确切的数字实际上是2.71828182......是欧拉以他自己命名了这个数字“e”，这个就是那个卡住无限数字的符号。

        普通的计算器只有4中运算：加减乘除。数字e实际上可以通过无限系列的加法、乘法和除法来计算如图3.5所示。约等于2.7182787698

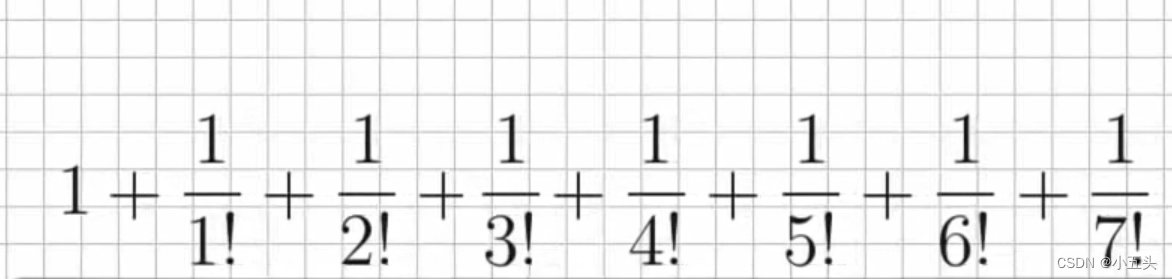
图3.5

        那么有乘法表示，就像把e写成1的幂。更一般化点就把e提到x的幂，那么无穷级数变成如图3.6所示。

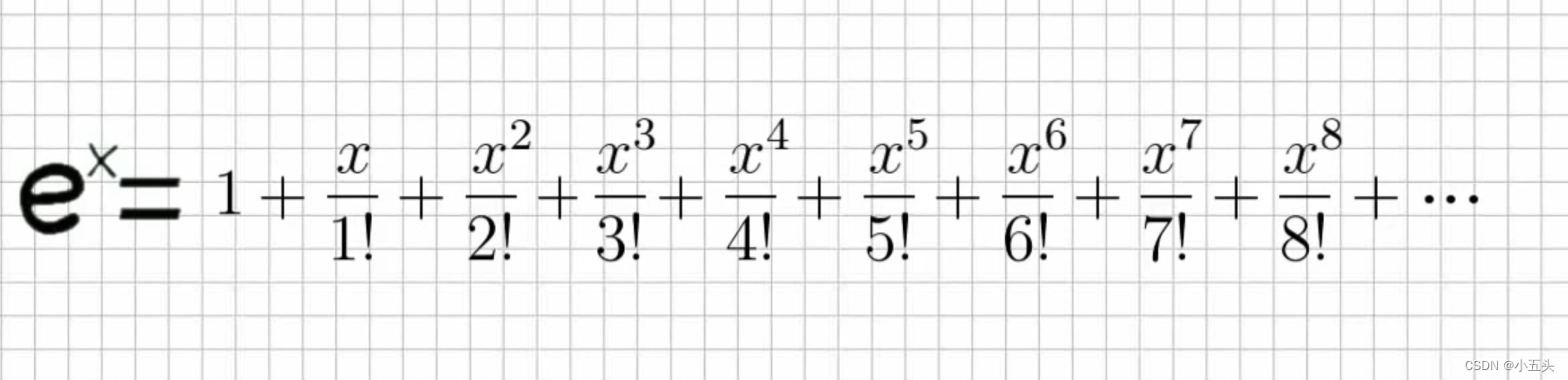
图3.6

        现在碰巧e到x并不是唯一可以通过这种无限级数计算的东西。三角函数正弦和余弦也可以用无穷级数来计算，x的正弦等于：x除以1阶乘 减去x平方3的阶乘加上x到5的阶乘减去x7的阶乘等等如图3.7所示。很容易预测这个系列的延续，当分母每次增加2时，我们增加的x的幂也的如此。每个项的正弦在加号和减号之间保持交替，x的余弦也会发生类似的事情。与正弦不同是，余弦是从2开始。正弦与余弦的无穷函数看起来与e非常相似。如果我们把余弦函数和正弦函数加在一起，也没有办法得到欧拉函数。因为在正弦和余弦中项直接的符号不断变化，而在计算欧拉数的系列中，不会出现这样的问题。所以为了使方程相等，我们需要乘以x平方的值必须等于负1。当x立方时也是如此，当x再次被提升到6和7的幂时，也是如此依此类推。当我们对一个数字进行平方时，结果总是正数，不是负数。所以这个时候出现了一个数学符号，虚数i就这样诞生了，i是唯一一个平方后得出负数结果得-1。

图3.7

        如果取欧拉数并将其增加，不是x的幂而是-1如图3.8所示。虚数乘以i的项用红色表示，实数项用蓝色表示，将它们从新排序后得到图3.9所示。其中所有虚数都乘以i因此可以将i进行分解。而实数项用来计算x的余弦值的项，虚数项用来计算正弦值的项并将其全部乘以i。因此欧拉数与余弦和正弦之间，只要将e增加到ix方并将正弦项相乘以i才能有效。所以这就是欧拉公式，也叫做最美公式如图4.0所示。欧拉的恒等式如图4.1所示。

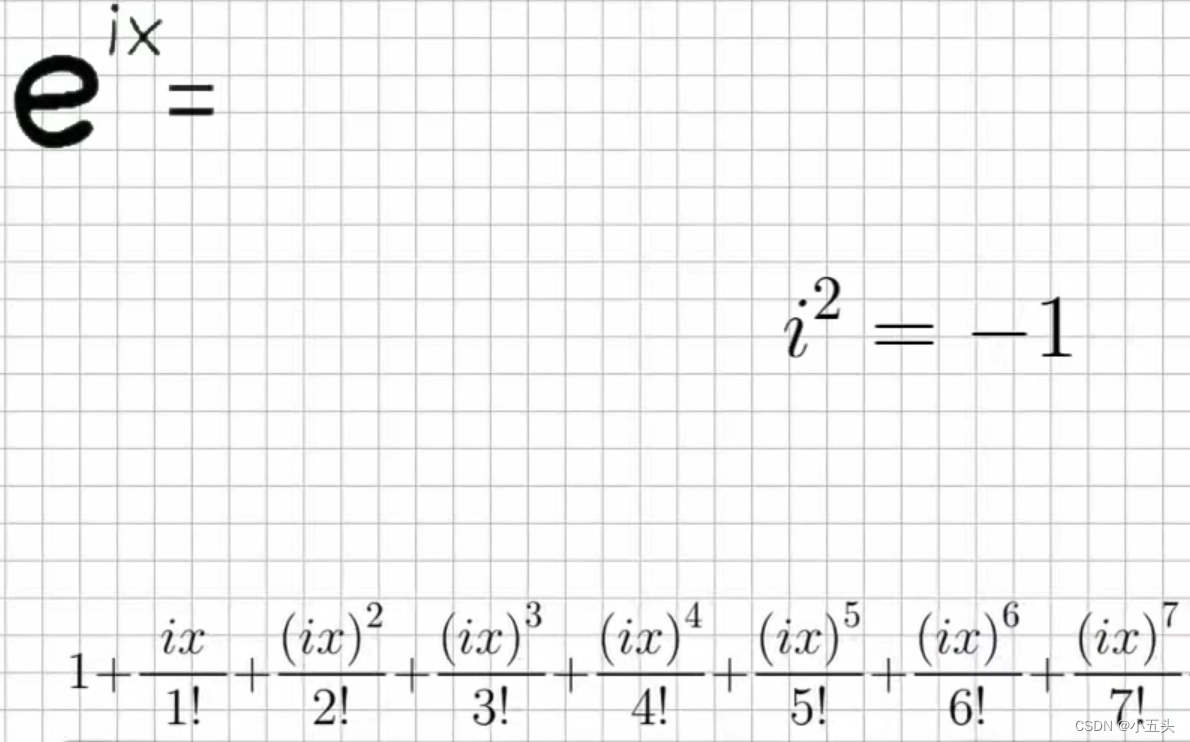
图3.8

图3.9

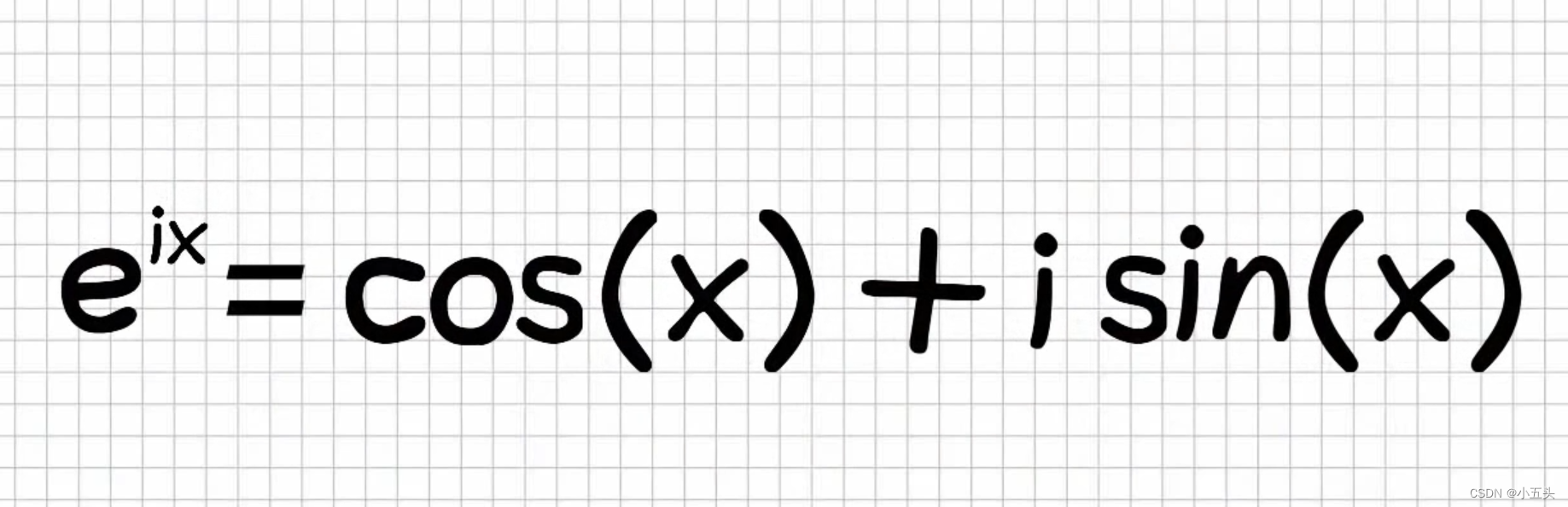
图4.0

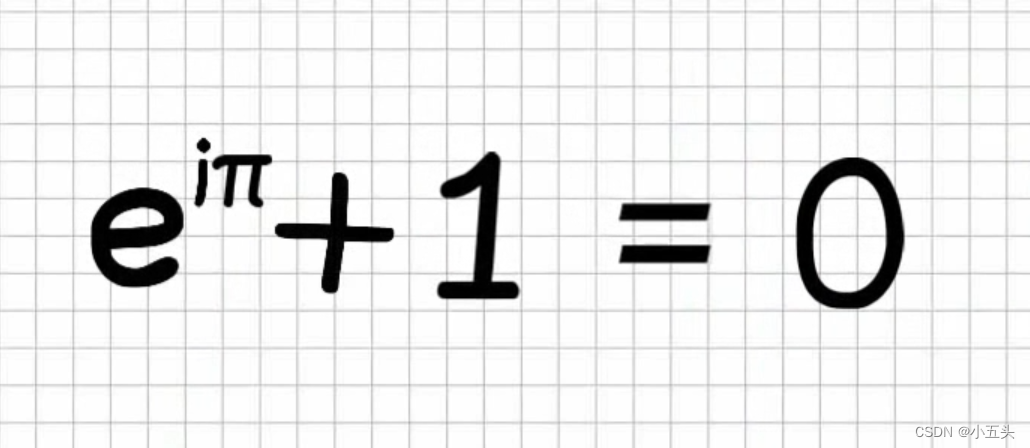
图4.1

 复数

        在傅里叶变化中，i起到了非常重要的作用。它将事物分开，将信号分解为其组成正弦波的算法。在此还需要用到关于相位，通过将频率相同但幅值不同的非相移余弦波和非相移的正弦波加在一起，制作任何相移的正弦波。用数学公式表达如图4.2所示，其中A是余弦波的幅度，B为正弦波的幅度。

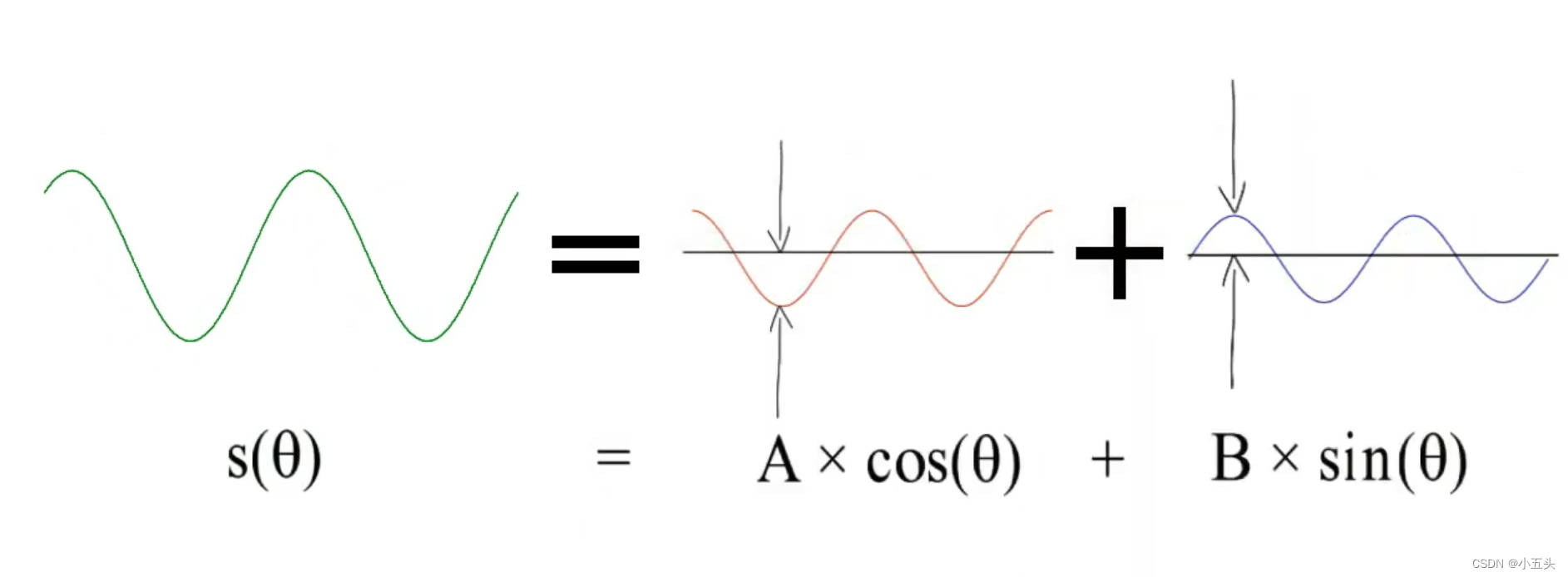
图4.2

        将图4.0用一种新型的表示法复数。复数是由实数和虚数构成的数。实数是我们日常生活中常见的数，例如1、2、3等等，而虚数是-1的平方根，通常用i表示。所以，虚数i的平方是-1，即i²=-1。 复数的一般形式可以写为a+bi，其中a和b都是实数，a称为实部，而b称为虚部。例如，3+2i就是一个复数，其中实部是3，虚部是2。同样地，我们也可以将实数看作是虚部为0的复数。例如，5可以写为5+0i。 复数的定义使我们能够更好地描述和操作一些实际问题。例如，在电路分析中，复数经常用于描述电阻、电感和电容等元件的阻抗。在量子力学中，复数被广泛应用于描述波函数和量子态。此外，在信号处理和图像处理领域，复数也被用来表示信号和图像的频谱。 复数之间可以进行加法、减法、乘法和除法运算，这些运算与实数的运算规则类似。例如，两个复数相加时，只需将它们的实部和虚部分别相加即可。而两个复数相乘时，则需要使用分配律和虚数i的平方等规则进行计算。 此外，复数还有一些其他的特性。例如，复数的共轭是指保持实部不变而将虚部取负的操作。如果一个复数的共轭与它本身相等，那么这个复数就是实数。我们也可以通过求模来计算复数的绝对值，即复数与原点的距离如图4.3所示。

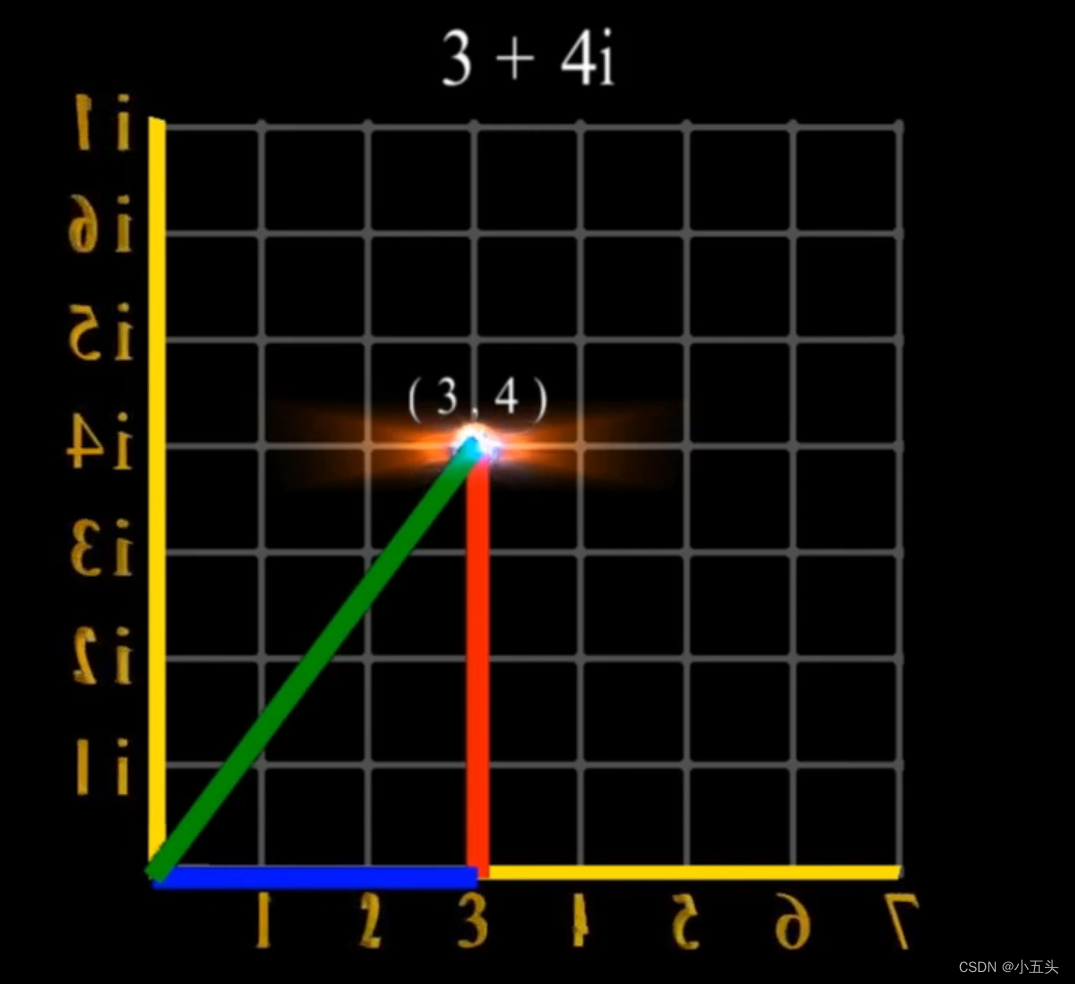
图4.3

       将三角形的底代表余弦波的振幅A。三角形的高度表示正弦波振幅B。这样会产生一个正弦波S振幅为5，由三角形的斜边表示，相移为53.1°，由三角形的角度表示如图4.4所示。 

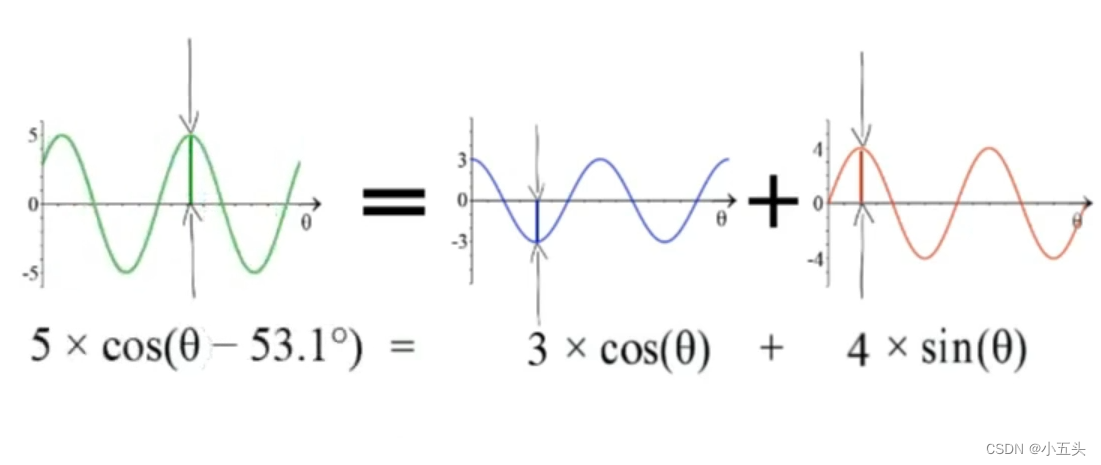图4.4

        还有另为一种计算三角形底边长的办法，是取角的余弦乘以斜边长度乘以53.1°的余弦等于3。而高度三角形的正弦值乘以斜边的长度5乘以53.1°的正弦等于4。所以可以这一种方式来描述复数点，用它的极坐标形式来写：5·cos（53.1°）+ 5i·sin（53.1°）。极坐标就是一个点，极点是指向该点的线。可以通过它的长度和角度来描述这条线。将复数的极坐标与欧拉公式联系起来，可以写成：5·e^(i·53.1°)。

        接下来，我们来看复数的四种基本运算：加法、减法、乘法和除法：

         1. 加法和减法: 加法和减法是最直接的，按照实部与实部、虚部与虚部分别进行加减即可。例如，(a+bi) + (c+di) = (a+c) + (b+d)i，(a+bi) - (c+di) = (a-c) + (b-d)i。

        2. 乘法: 复数的乘法稍微复杂些，需要按照乘法分配律进行计算。如，(a+bi) * (c+di) = ac + adi + bci - bd = (ac-bd) + (ad+bc)i。

        3. 除法: 复数的除法最为复杂，需要通过乘以共轭复数来进行。例如(a+bi) / (c+di) = (a+bi) * (c-di) / ((c+di) * (c-di)) = [(ac+bd) + (bc-ad)i] / (c^2+d^2)。

        指数乘积规定：对于任意实数a和b，指数乘积规定可以表示为： a^b = e^(b * ln(a)) 其中，a^b表示a的b次幂，e是自然对数的底数，ln(a)是a的自然对数。 性质 指数乘积规定具有多个重要的性质：

        1. 根据指数乘积规定，a^(b+c)等于a^b乘以a^c。这个规则对于简化复杂的指数计算非常有用。

         2. 指数乘积规定使得两个数的乘积可以转化为它们各自的指数函数之积。例如，a*b可以表示为e^(ln(a) + ln(b))。

        3. 指数乘积规定还可以转化为对数运算。具体来说，如果a^b=c，那么ln(a^b)等于b * ln(a)，即ln(c)。

        例如欧拉函数，可以以指数的形式将它写出，则完全相同的方法适用于a+bi·c+di。以3+4i·9+2i为例，为此可以使用勾股定理和反正切原则。对3+4i：3的平方加4的平方在开根号等于5。使用反正切acrtan（4/3）≈53.1°。对9+2i进行一样的操作如图4.5所示。

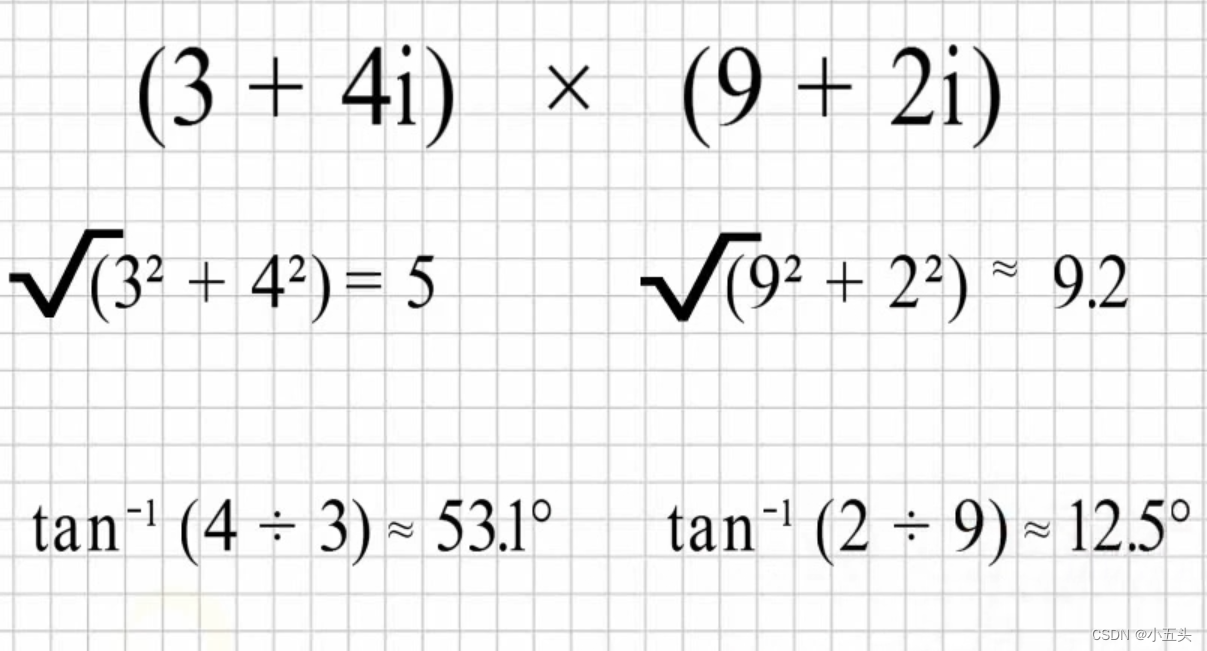
图4.5

        将乘法改写成5e^(53.1°·i)  · 9.2e^(12.5 °·i)得出结果：46e^(65.6°·i)。接下来可以使用Polar形式将其转换回笛卡尔形式，并表明这俩种方式给出的答案如图4.6所示。利用复数的乘法与除法即可算出结果0.41+0.35i。

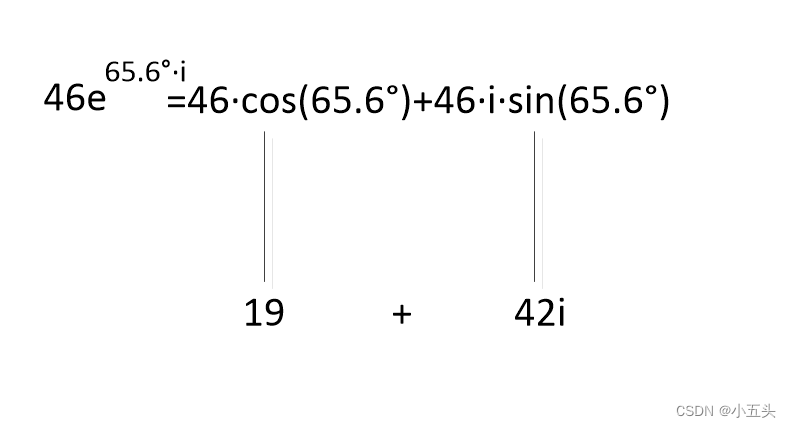
图4.6

 傅里叶级数

        变量的任何函数，无论是连续的还是不连续的，都可以在变量的倍数的一系列正弦中展开。傅里叶将任何信号视为许多正弦波，每个正弦波都有自己的频率相位和幅度，全部加在一起。这就是转换一种从更简单的构建中构建信号的方式。但傅里叶绝不是唯一一个发明变化的人。还有许多其他类型的转换，例如拉普拉斯变换就完美的克服了傅里叶的一大缺点。

       拉普拉斯变换的定义如下： 对于一个定义在非负实数集上的函数f(t)，其拉普拉斯变换F(s)定义为积分形式，即： F(s) = ∫[0,∞) e^(-st) f(t) dt 其中，s是复变量，可以是实部和虚部都大于零的复数。拉普拉斯变换的本质是将时域函数通过指数衰减的方式映射到复平面上的一条曲线，这样可以方便地进行频域分析和求解微分方程。 拉普拉斯变换的一个重要特性是线性性质。即，对于任意两个函数f(t)和g(t)，以及对应的拉普拉斯变换F(s)和G(s)，有以下等式成立： a*f(t) + b*g(t) ↔ a*F(s) + b*G(s) 其中，a和b是任意实数。这个特性使得拉普拉斯变换在信号处理和系统分析中非常有用，可以方便地进行信号加权、线性组合和系统响应的求解。 另一个重要的特性是微分和积分的关系。对于一个函数f(t)的导数f'(t)和拉普拉斯变换F(s)，有以下等式成立： f'(t) ↔ s*F(s) - f(0) 其中f(0)是函数f(t)在t=0时刻的初值。这个特性在求解微分方程和系统响应时非常有用，可以将微分方程转化为代数方程，从而简化求解过程。

        小波变换的定义如下：首先，它能够提供信号在时间和频率上的局部信息，使我们能够更准确地分析信号的瞬时特征。与传统的傅里叶变换相比，小波变换能够在时间和频率之间建立更好的平衡，从而在处理非平稳信号时更为有效。 其次，小波变换具有多分辨率分析的能力。它能够将信号分解成不同尺度的子信号，使我们能够在不同频率范围内捕捉到信号的细节和特征如图4.7所示。

图4.7

  卷积

        信号是指随时间变化的物理量，例如声音、图像、电压等。在数字信号处理中，信号通常以离散的形式表示，即在一系列离散时间点上取样得到的数值序列。 卷积是一种数学运算，用于描述两个函数之间的关系。在信号处理中，我们通常将信号表示为离散时间上的函数，因此，信号卷积可以看作是两个离散函数之间的运算。 信号卷积的定义如下：给定两个离散函数f(n)和g(n)，它们的卷积记作f(n)*g(n)，定义为： f(n)*g(n) = ∑[f(k)g(n-k)] 其中，k为求和变量，取值范围为整个定义域。换言之，卷积是将两个函数按照一定规则进行加权求和得到一个新的函数。

        卷积的工作原理：我们可以想象一下，当窗口滑动到某个位置时，它会与该位置及周围的数据进行相乘，并将相乘结果相加，得到一个新的数值。这个新的数值就是卷积运算的输出值，它可以被用于后续的处理或分析。 卷积的工作原理看似简单，但却非常灵活。它可以通过调整窗口的大小、形状和滑动的步长来实现不同的效果。

        为了找到具有我们在信号中寻找的频率的正弦波的相位，我们可以做完全相同的事。在信号上滑动或卷积相同频率的余弦波。如图4.8所示，称红色的余弦波为测试波。之所以不使用正弦波是因为使用傅里叶公式，先计算余弦后计算正弦如图4.9所示。

图4.8

图4.9

        所以测试波为一个余弦波，通过增加它的相位慢慢的将它划过原始信号。当测试波与原始信号汇聚时，就已知在原始信号中找到了正弦波的相位。但是电脑无法识别则操作，所以需要生成一个数字，一个表示两个信号匹配程度的分数。当它们完全不匹配时，则分数很低。当它们完全匹配时，分数很高。

        现在将测试波上面的每个点与原始信号进行相乘，并将相乘后的信号绘制到新的二维图上。在0度的角，测试波值为1，正弦波值为0.17所以两个点相乘，得0.17,。以此类推如图5.0所示。

图5.0

        然后测量由“乘法图”包围的区域，会得到一个单一的值，这个是测试波和原始信号正弦波匹配程度的分数如图5.1所示。随着测试波的平移分数也会随之改变。随着测试波越来越接近原始波形相同时，乘法图所包围的区域会增加，也就意味着分数也随之增加。当两个波相同时，分数达到最高值180，随着测试波划出分数再次下降。当两个波最异相时，分数达到最低值-180。

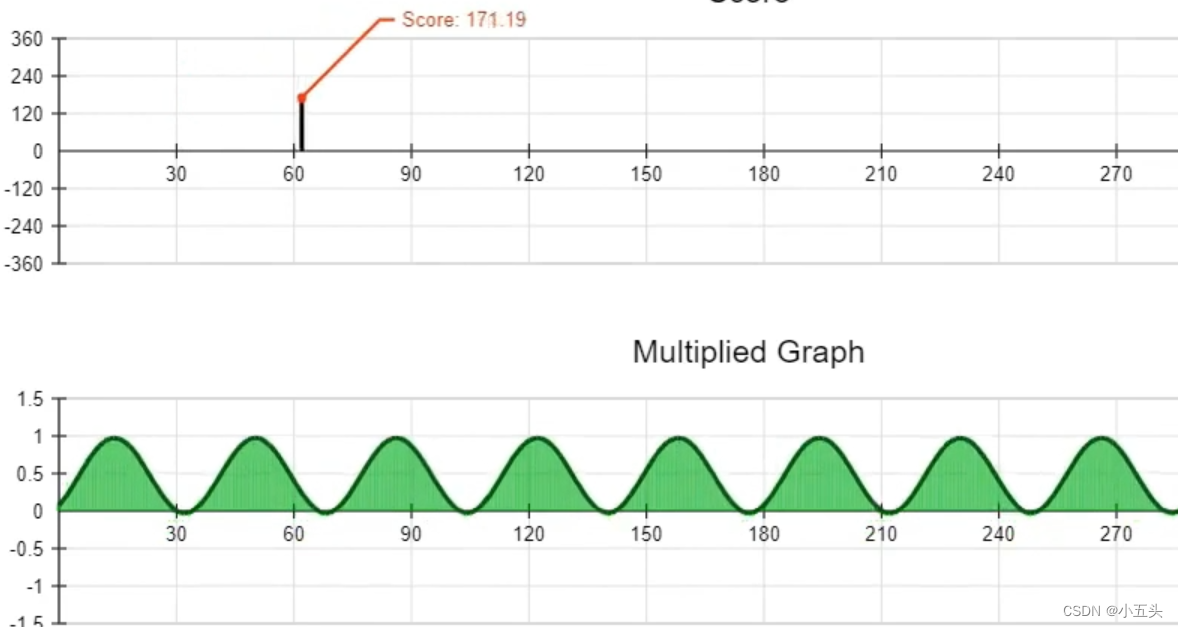
图5.1

        因此得出结论，当测试波达到180°相位时，两个信号完美匹配得分数处于最高值。可以在信号中找到了正弦波的相位。

        接下来这是一个不规则的信号，让我们首先将频率为1、幅度为1、的测试波与原始信号进行卷积如图5.2所示。

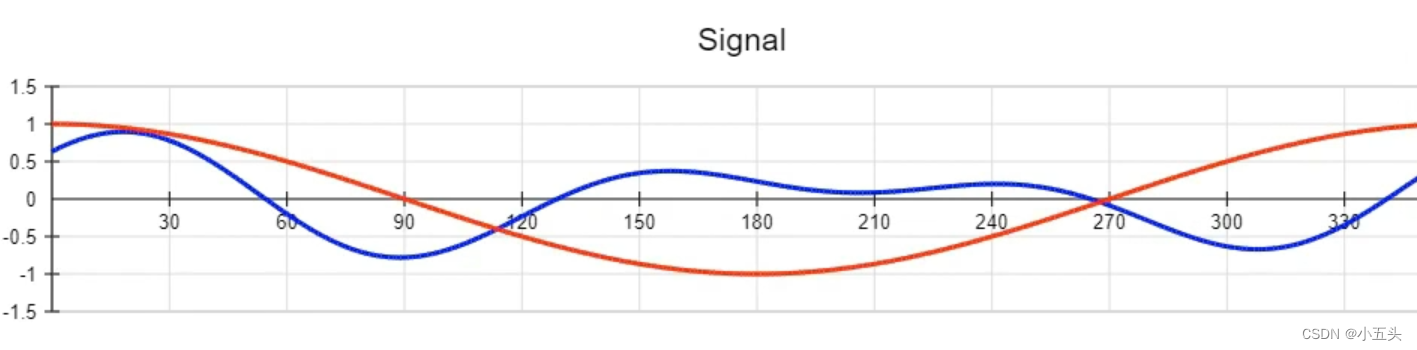
图5.2

        当我们将测试波上的所有点乘以信号上的所有点，并将其绘制在相乘图上，相位是什么并不重要，x轴上方的图所包围的面积总是与在它下面。这意味着当我们计算图形所包围的总面积时，得到的分数为0分如图5.3所示。这就表明我们的原始信号中不包含频率为1的正弦波。在此基础上逐步增加使用频率为2的正弦波对原始信号进行卷积。可以看到随着相位的增长，乘法图在上下移动，分数也在随之上下移动如图5.4所示。因此原始信号中确定包含频率为2的正弦波。找到分数的最高点分数90在相位30°的时候。再次进行卷积这次使用频率为3的正弦波对原始信号进行，乘法图上下移动，分数也在上下移动。说明在原始频率中包含频率为3的正弦波，分数在60°相位处达到最高值72，因此正弦波相位为60°。使用频率为4正弦波进行卷积，分数为0。得原始信号中不包含频率为4的正弦波。

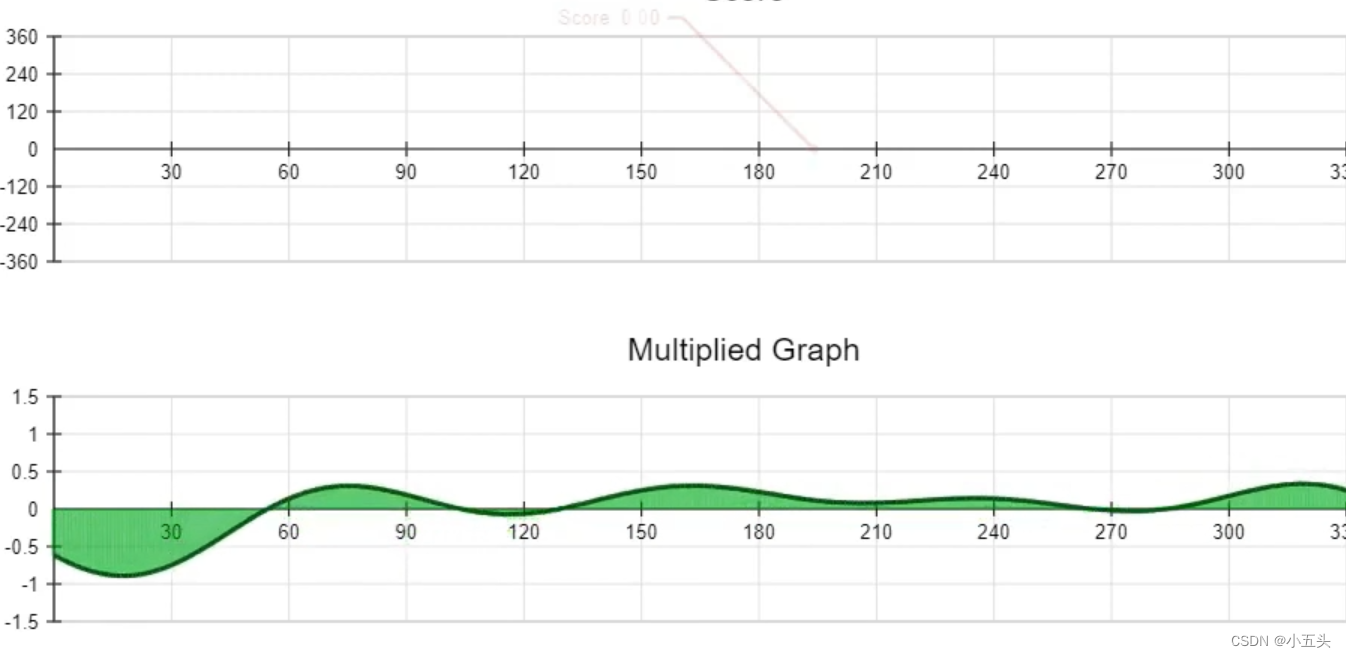图5.3

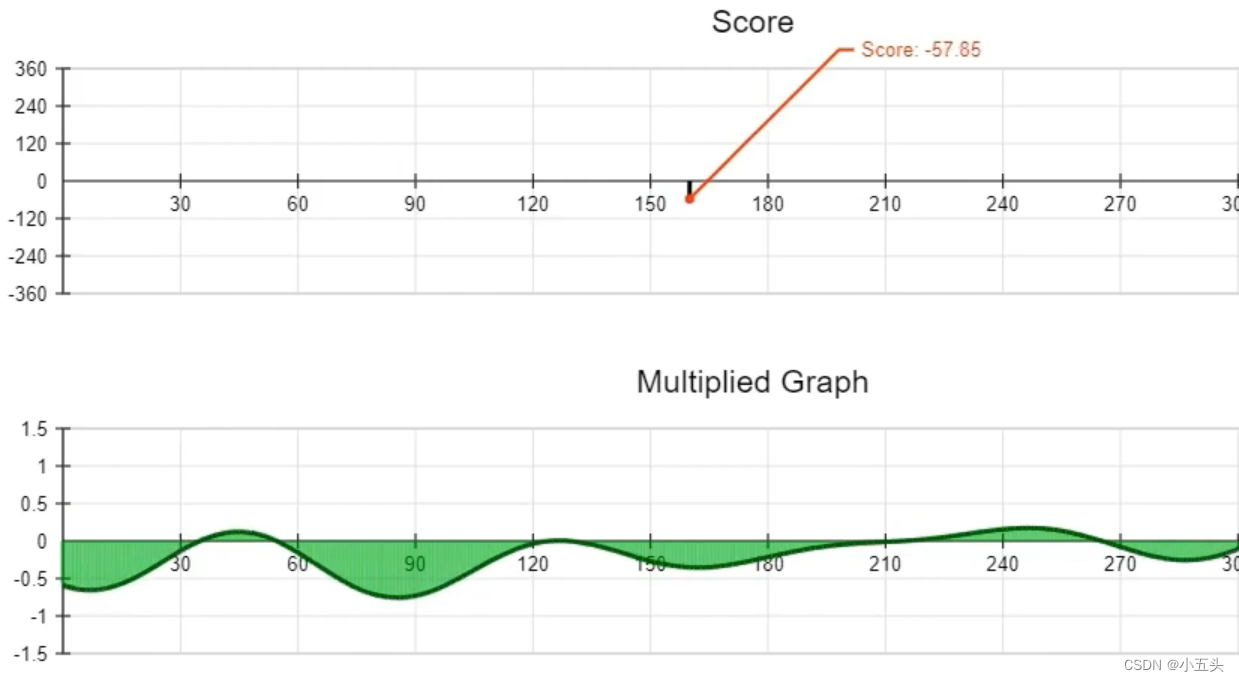
图5.4

        所以每当尝试信号中不存在的频率时，无论那个阶段，分数为0，当信号中确定存在频率时，会得到一个非零的分数值。当找到分数最大点时，就找到了正弦波的相位。为每个频率找到的最大分数正是正弦波的幅度成正比。

        通过将分数除以信号周期的一半，这个信号周期是360°，所一半为180°，对于这个测试波频率为3，最高分数为72。所以72/180=0.4这是实际信号中改频率的幅度。这个原始信号已经得出结论是由两个频率的正弦波组成的，第一个频率为2、相位为30°、相对振幅为90。第二个频率为3、相位60°、相对振幅为72如图5.5所示。当两个正弦波加在一起时，得到的结果看起来就想原始信号。因此使用卷积，已经成功的将原始信号分解为正弦波的组成，这就是傅里叶级数。 

图5.5

       任何相移的正弦波都可以，通过添加一个频率相同但幅度不同的非相移余弦波和一个非相移正弦波来描述。所以不必执行整个卷积操作，只需要先将我们的信号乘以余弦波，然后乘以正弦波使用Phythagoras和反正切，从两个分数计算幅度和相移每一波。

        上述出现的第一个频率是2，如果使用非相移余弦波作为测试波计算分数，得到78，则使用非相移正弦波测试波计算分数，得到45，使用勾股定理78平方根+45平方根等于90。在使用反正切最终得30°，与直接卷积算出来的答案一致。

  卷积二

        傅里叶变换将一个函数从时间域转换到频率域。在时间域中，我们可以看到函数随着时间变化的情况，而在频率域中，我们可以看到函数中包含的不同频率成分。 傅里叶变换的数学表达式是： F(ω) = ∫[f(t) * e^(-iωt)] dt 其中，F(ω)是函数在频率域的表示，f(t)是函数在时间域的表示，e^(-iωt)是一个复指数函数，ω是角频率。 傅里叶变换的工作原理可以通过以下步骤来理解：

         1. 首先，我们选择一个函数f(t)，它可能是一个信号或图像等。

         2. 然后，我们将这个函数表示为一系列复指数函数的和，每个复指数函数具有不同的频率和幅度。

         3. 这些复指数函数与函数f(t)进行内积运算，以获得在频率域中的表示。

         4. 最后，我们得到一个频谱，它显示了函数f(t)中包含的不同频率成分的强度和相位。

        提取了一段来自小提琴的声音信号与余弦波相乘时得到的结果如图5.6所示。现在需要找到乘法信号图下的区域，以获得表示该余弦波对整个信号的贡献幅度分数。想要计算一个矩形的面积，可以用矩形的高度乘以宽度。所以可以将信号做成很多矩形，划分成很多片，把每一片当作一个矩形，然后把所以矩形的面积加在一起如图5.7所示。 可以看到矩形块如何近似于相乘信号的形状。再次减少每个矩形直接的宽度，并增加矩形的数量，会得到一个更好的近似值。矩形越薄，数量越多，就越接近真实信号的面积值。

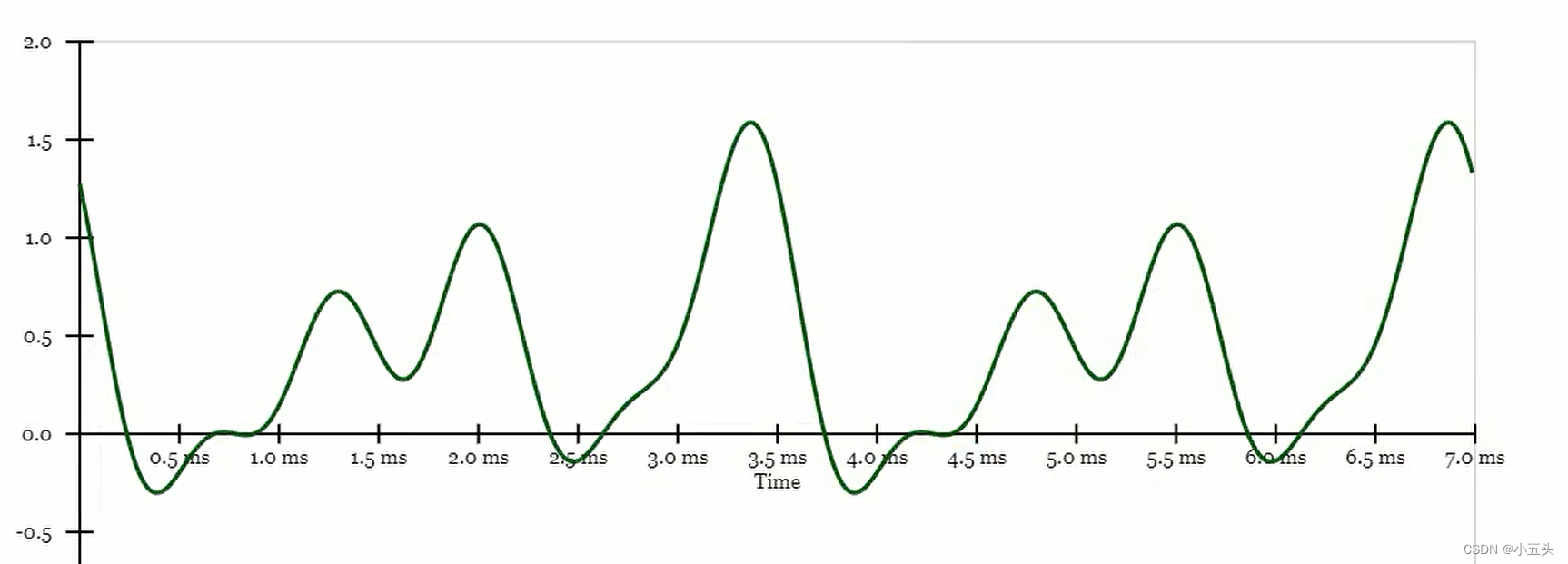
图5.6

图5.7

       如果每个矩形无限薄，并将矩形的数量增加到无穷大，可以精确计算面积。这称为积分，在数学上表示∫。因此为了找到乘积余弦图下的面积，取乘积信号x的t乘以cos2πft相对于t的积分，即每个切片的厚度为t秒，其中一个t和下一个t之间的差异无限小。在数学上将其写为：∫x(t)·cos(2πft)dt的积分，积分的上下限在信号的一个周期就足够了，因为此信号周期完成后，该信号只会重复自己。在原始信号中，没3.5毫米所有内容都会重复一次，因此信号周期为3.5毫秒。因此积分的时间等于0和3.5毫秒之间如图5.8所示。

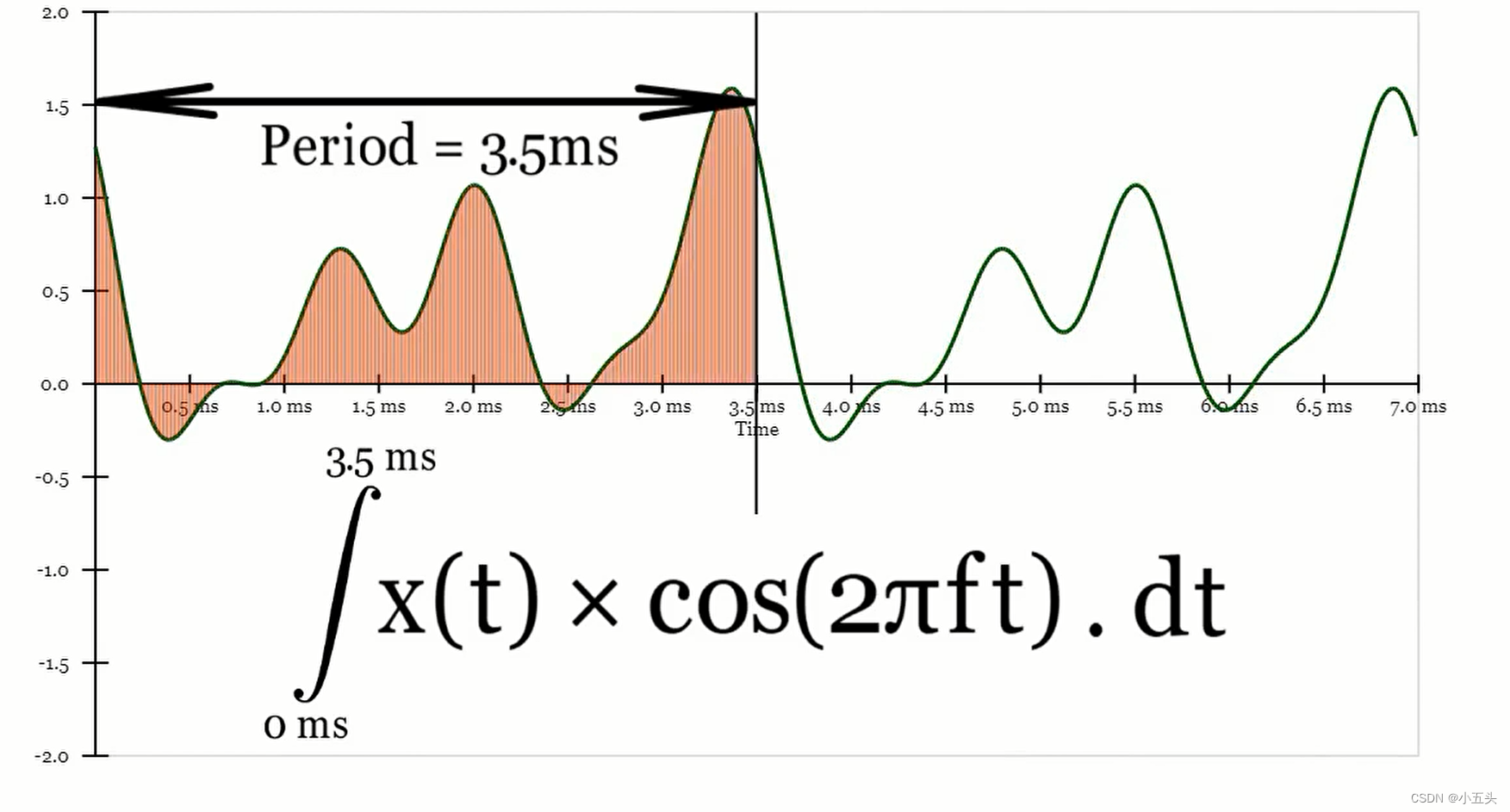
图5.8

        现在由于这是一个重复的信号，只要咋子恰好1个周期内进行积分，哪里设置限制实际上并不重要。假设这个信号一直持续下去。信号会一直一直重复下去。也可以在-1.75毫秒到1.75毫秒进行积分，最终结果依然是一样的，只要积分的时间保持好3.5毫秒。（只限于这个特殊的信号）

        可以通过上述公式计算出第一个频率的余弦波对原始信号的贡献程度分数。重复刚刚的所有步骤，只是现在使用相同频率的正弦波。将原始信号乘以正弦波，然后积分使用数学公式表达：∫x(t)·sin(2πft)dt得到的该正弦波对原始信号贡献幅度的分数。

        现在已经有两个独立的积分，称之为余弦积分和正弦积分如图5.9所示。如果想将两个公式合二为一，那么必须要用到函数i，如果将正弦积分乘以i就可以将两项积分进行相加处理，甚至将一个与另一个相减，也不会对结果产生任何影响，因为i将他们分开。

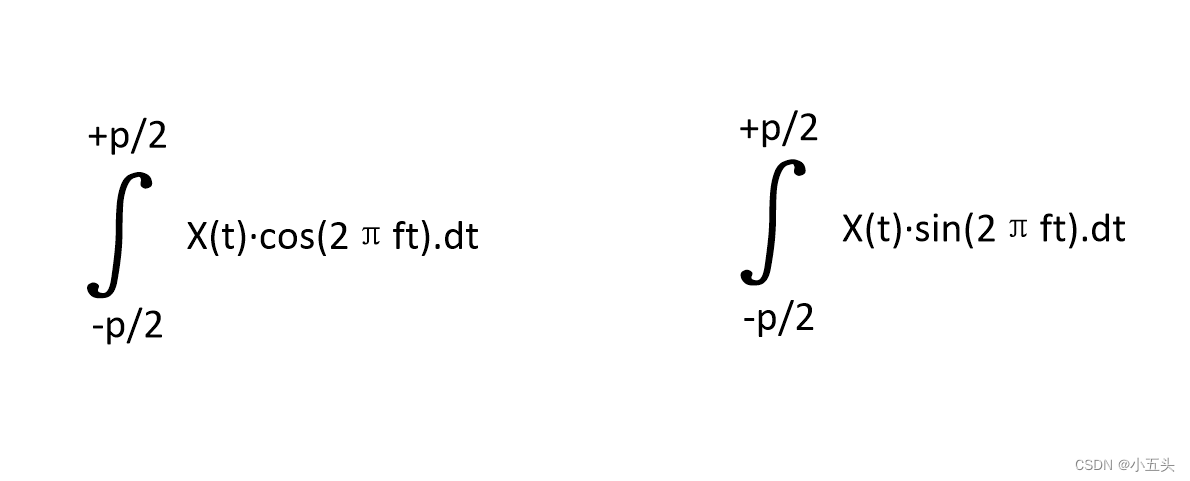
图5.9

        在进行组合之前，我们要知道傅里叶变化是一种将信号分解为其组成正弦波的方法。因此如果傅里叶知道如何分解信号，他也可以将这些正弦波重新组合在一起以恢复信号，并且确定可以使用傅里叶逆变换如图6.0所示。

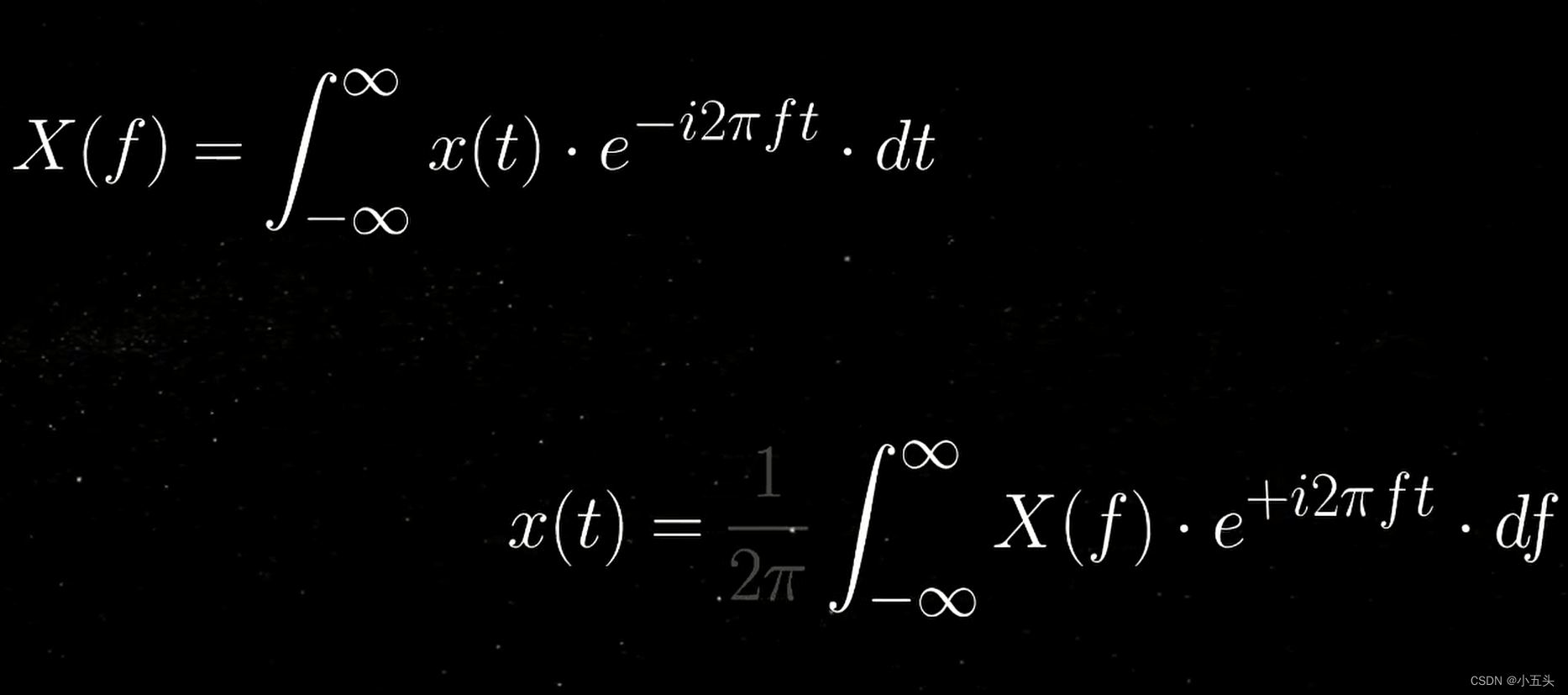
图6.0

        将两个信号的积分合并为一个，不会改变结算结果。 因为i将两项式子分开不会改变结果，t信号x乘以正弦项和余弦项，可以将其作为公因式提出,并将其它所有内容放在括号中。在通过欧拉公式将括号内的数据进行转换如图6.1所示。这项公式诠释了在我们第一个测试频率下计算余弦和正弦项的分数。现在需要对许多不同频率一次又一次的运行这个方程，可以通过不断改变“f”的值做到。

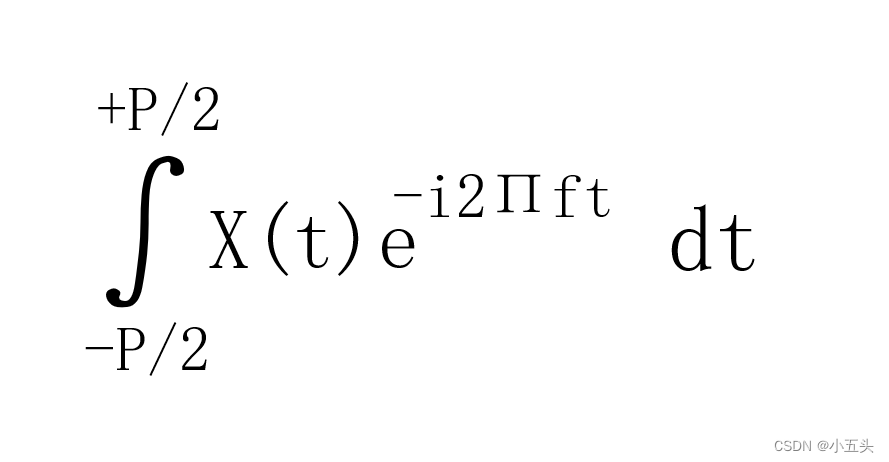
图6.1

        公式中n是一个索引如图6.2所示，当n等于1时，我们用第一个测试频率F(1)测试我们的信号，得到结果C(1)。其中C(1)是一个复数，实部值代表余弦波在频率1的分数，而虚部代表正弦波在频率1的分数。当n等于2时，用下一个频率F(2)测试原始信号，显然易见得到的结果也是C(2)以此类推。这是傅里叶级数原理。

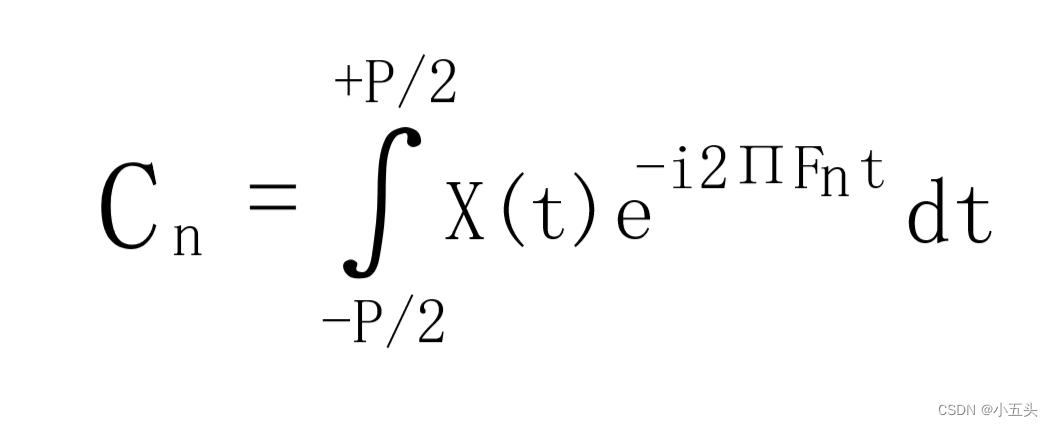
图6.2

 傅里叶变换

        傅里叶级数非常适合模拟重复信号，但重复信号不携带任何新信息。我们在日常生活中遇到的绝大多数信号都不会重复。因此对于那些，则需要用到傅里叶变换。

        下述方程如图6.3所示在表面上看确实相似，但是它们之间有两个重要的区别。首先是积分的限制不同，在傅里叶级数方程中，积分的范围从信号周期的负一半到信号周期的正一半，而在傅里叶变换方程中，它是从负无穷大到正无穷大。其次傅里叶级数中的频率项F有一个小下标n，这个下标n也会出现在方程的结果中。但是在傅里叶变换方程中，没有这样的下标n所以方程的结果大不相同。

图6.3

        积分是在图表下面积的地方，在傅里叶级数中使用该值作为分数来告诉我某个频率对整体信号的分数有多大。积分的极限表示正在查看多少图。在傅里叶级数中，只需要查看信号的一个周期，因为在该周期完成后，信号会重复。而在傅里叶变换中，需要查看整个信号，这样做的原因是想要对永不重复的信号进行建模，因此没有循环，所以需要从时间开始到时间结束。时间是无穷的所以需要查看从负无穷到正无穷的信号。

        指数信号，就像它的名字所暗示的那样，继续以指数增长，在负数部分可能很小，单从某一刻开始，当时间为零时它会随着时间迅速增大。所得傅里叶无法对此信号进行求解。傅里叶算法的初衷是用于查找信号中存在的正弦波，如果将信号诚意给定频率的余弦波，其次测量乘法余弦波信号图特定频率下的分数。在将原始信号与特定频率的正弦波进行相乘计算积分得出分数。以此类推直到找到信号中的所有频率。最终结果只会等于0；

  傅里叶的离散型

        在上述中描述到，项C(n)实际上是一个复数列表，每个复数代表一个具有不同频率幅度和相位的下标n是正弦波。当f下标改变时也会出现相同的频率如图6.4所示。以此类推如果想要取该列表中的每个正弦波并将它们加在一起得到结果的波，看起来就像我们的原始信号。傅里叶变换方程中的任何地方都没有这样的下标n，因为与傅里叶级数给出的正弦波列表不同，傅里叶变换为我们提供了一个连续的函数，通过测试连续的频率列表产生的sin(x)由字母F表示。

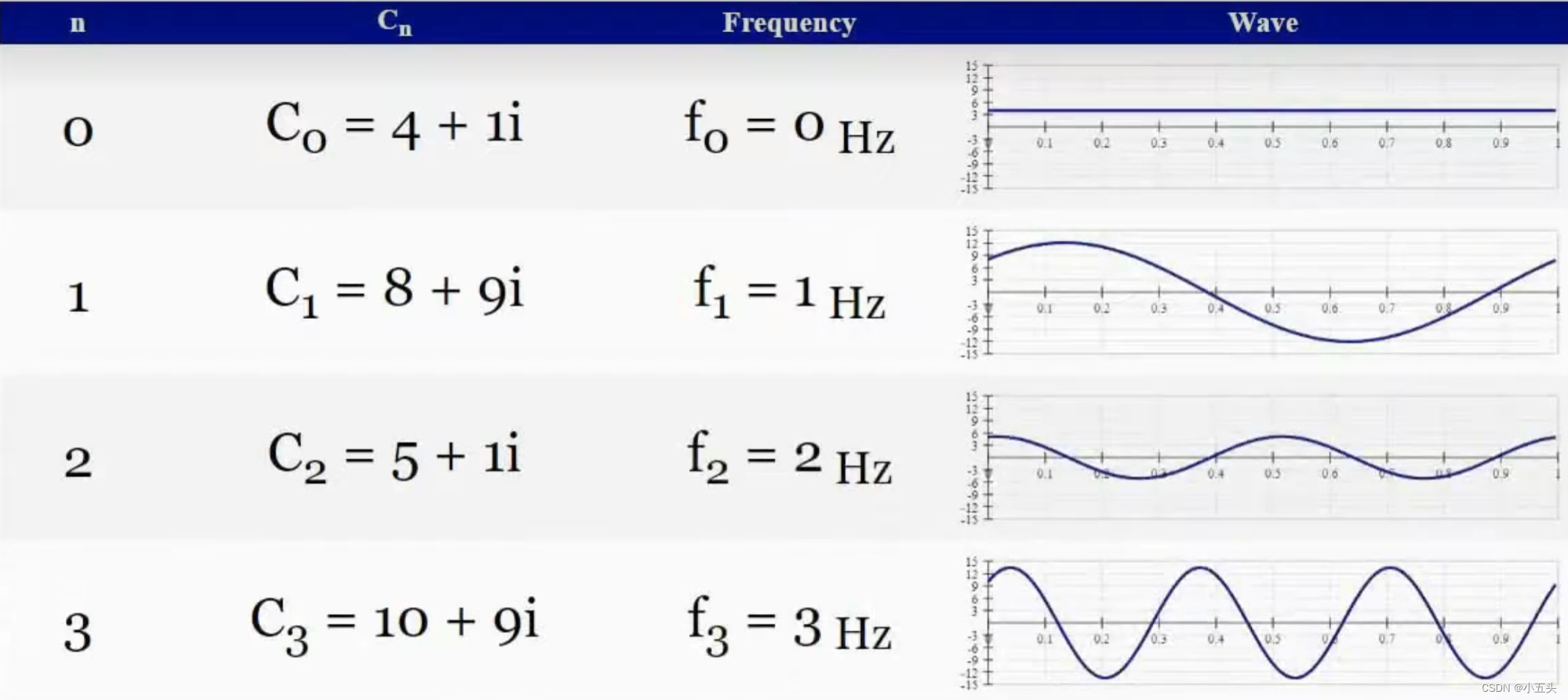
图6.4

        信号的带宽意味着从信号中的最小频率到最大频率，每个频率都在某种程度上存在，这就是为什么没有在傅里叶变换方程中任何地方都下标n，因为根本无法为傅里叶变换表示的信号中的每个频率单独编号，因为从最小频率到最大频率有无数个中频。

   傅里叶变化

        首先介绍一下卷积公式如图6.5所示。其中F(τ)是任意函数，函数就是信号的另一种叫法。τ信号如图6.6所示。g给定一个余弦信号（之所以选用余弦是应为，余弦波反转后还是余弦波，而正弦波反转后是-正弦波），将两个信号绘制在同一个二维坐标系中X轴作为时间系，随着时间的变化移动余弦信号，并将两个信号相乘将结果绘制一个新的二维坐标系中。随着t的变化两个信号的乘积在x轴上上下下移动如图6.7所示。

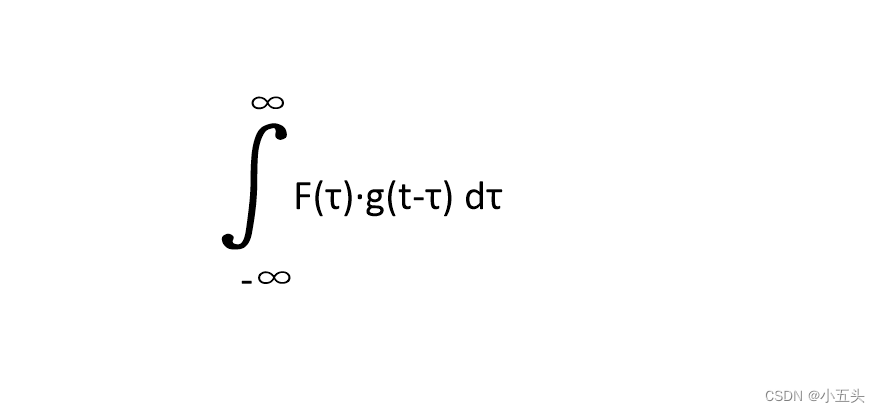
图6.5

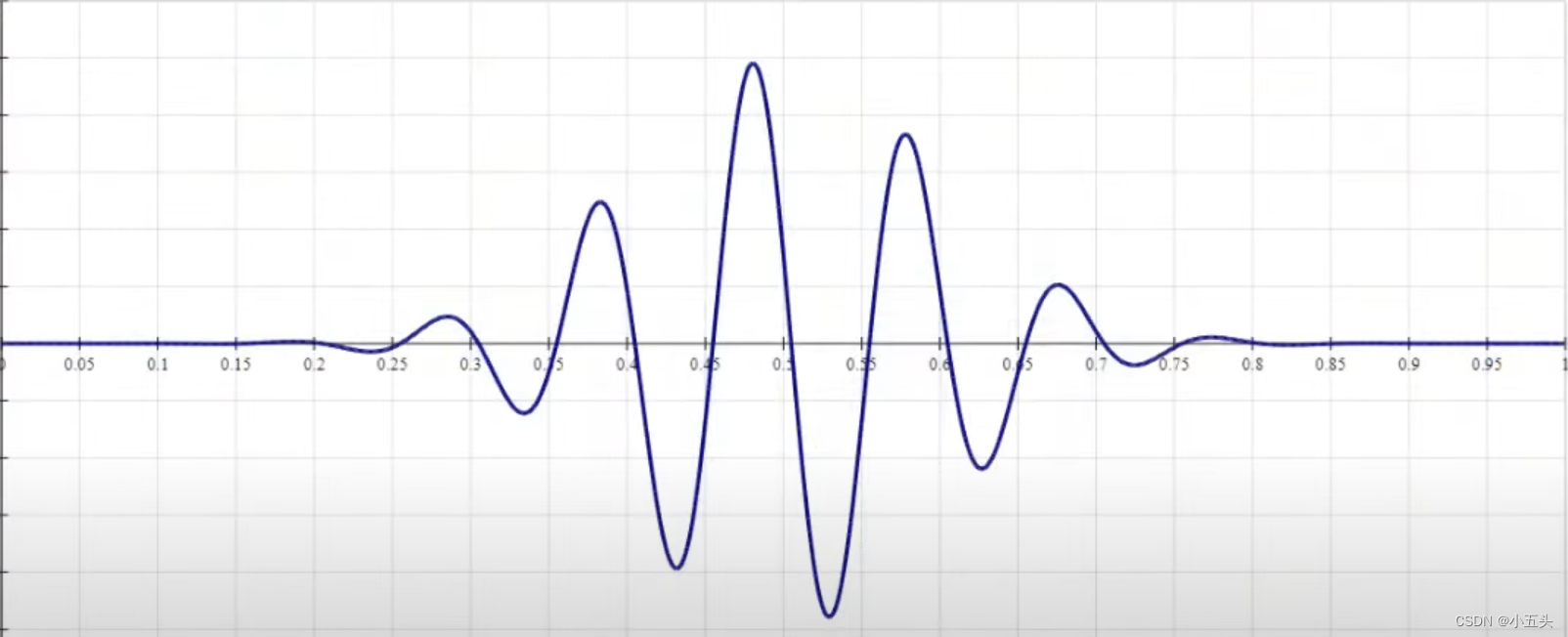
图6.6

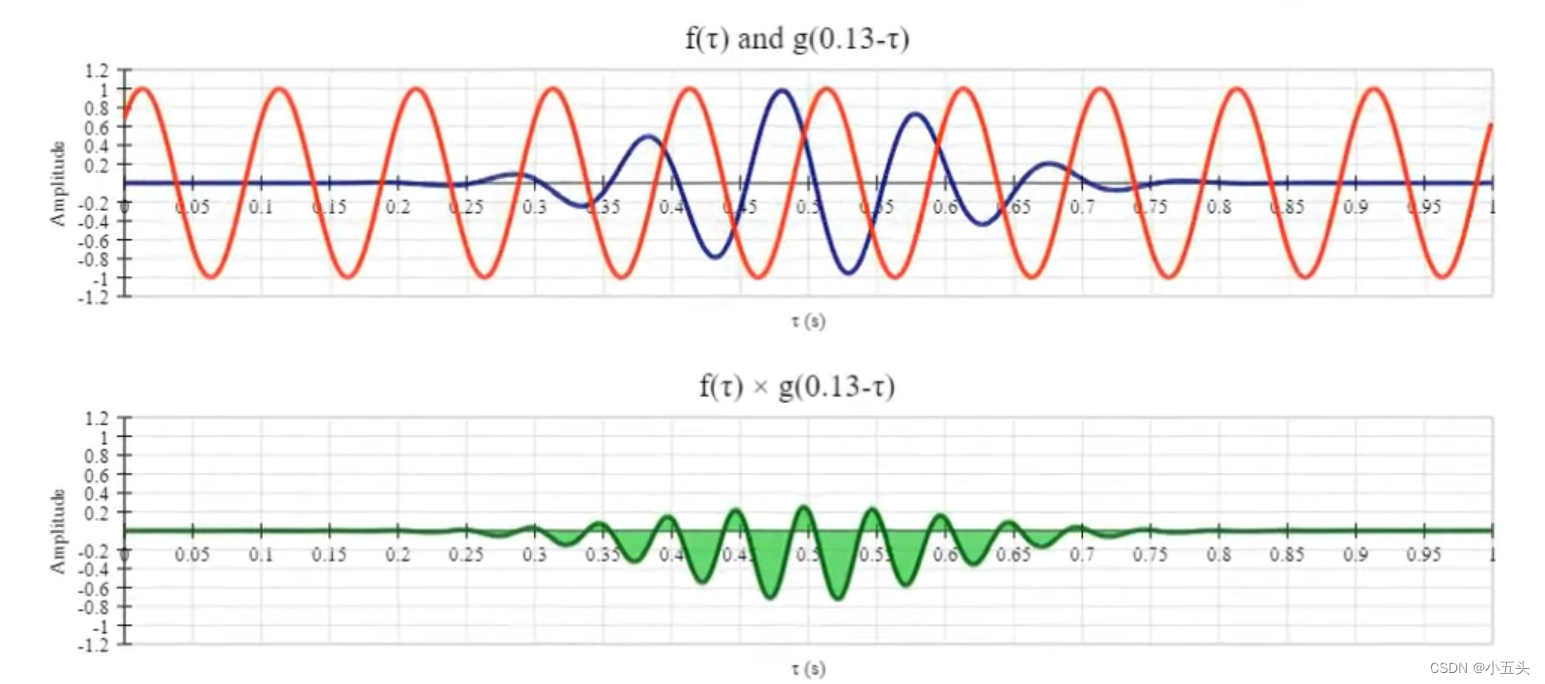
图6.7

        当乘积结果达到最大值时，此时的分数会告知匹配程度如何。这就是傅里叶卷积，傅里叶变化转换信号从时域进入频域，任何信号都可以构建不同频率的正弦波，而傅里叶变化告诉我们信号中存在那些频率。将结果得到的分数对应每个频率绘制图表，将频率防止X轴，Y轴防止对应频率的最高分数如图6.8，这就是傅里叶变化对此信号。

图6.8

        拿到余弦波与原始信号卷积后的的分数与正弦波与原始信号卷积后的的分数。如同一频率下余弦波为0.039正弦波为-0.119，使用勾股定理公式可以计算出：√0.039平方+-0.119平方=0.125（幅度）。而相位公式为：acrtan（-0.119/0.039）。

 快速傅里叶

        随机获取一段信号，将此信号进行傅里叶变换，变换后的结果如图6.9所示。每行在该列表中表示不同的正弦波。正弦波有三个属性：频率，幅度和相位。在傅里叶变换开始时，它并不知道原始信号是由那些正弦波构建的，所以从理论上讲，它需要测试无限数量的不同正弦波，覆盖所有不同的可能性，显然无法在计算机中做到这一点。因此必须更有选择性并且测试有限数量的正选曲线。

图6.9

        频率：所获取的N项结果全部在列表中，K为每的索引，N为列表中的项目总数，R为采样率。计算每项的频率公式：F=k/n·R。举个例子，假设我想找到此列表中第二项的频率，如上图所示它的索引K为1，以采样率对信号进行采样，R=50Khz，有1024个采样点，代入公式：F=1/1024·50 得48.83Hz。现在知道了每一项的频率如何求得，

        复数的实部表示余弦分量，虚部表示正弦分量。当然这些数字用三角形也可以表示。想象一下在一个圆圈内旋转的三角形，随着三角形角度的增加，它的高度增加，一担角度通过90°，高度再次开始降低，当角度超过180°时，高度开始增加但是方向相反，一担角度超过270°，高度就开始了再次减少，一切都重新开始。如果将其绘制在带有角度的二维坐标系中，X轴上是三角形的高度，在y轴上只需要看它描述了那个功能如图7.0所示。

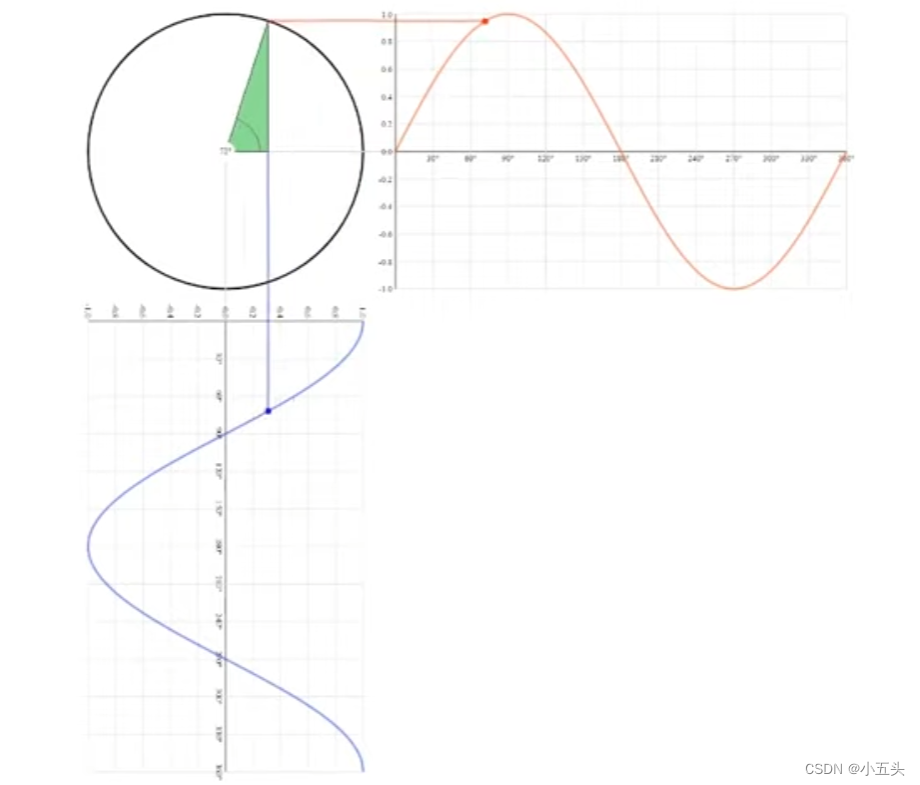
图7.0

        证明正弦波和余弦波与三角形相连，选择第3项用作计算它所代表的正弦曲线的幅度和相位。（复数描述的余弦波和正弦波的振幅），如果要求正弦曲线需要另做运算。

        实例，制作三角形的宽度等于复数的实部表示余弦波的振幅，三角形的高度等于复数的虚部表示正弦波的振幅。将正弦波与余弦波进行相加得到正弦曲线，通过勾股定理计算得出正弦曲线的幅度如图7.1所示。

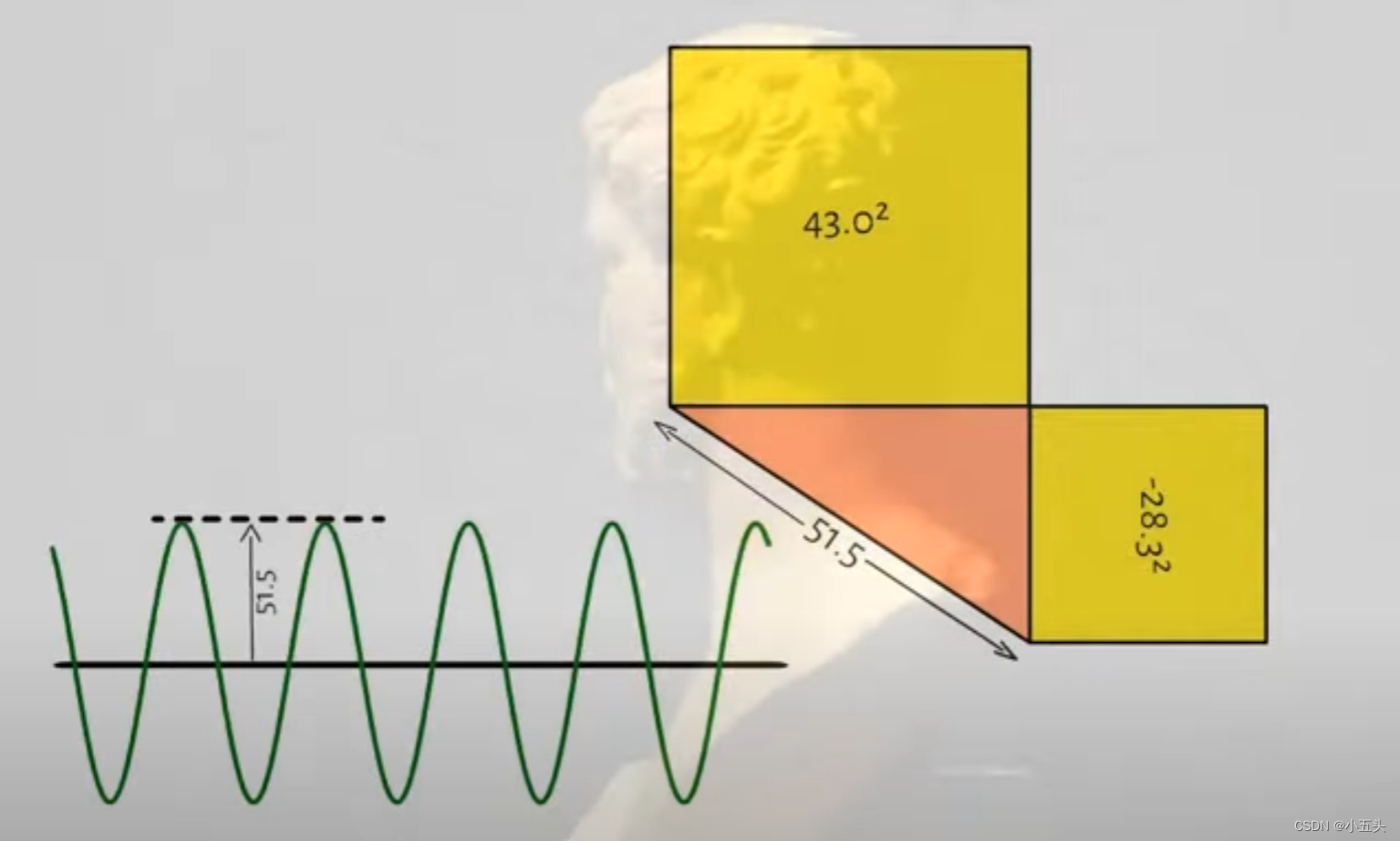
图7.1

        三角形的角度与其宽带及其高度，增加高度角度增加，反之亦然增加宽度角度较小，反之亦然。但是三角形的高度和宽度不是线性的，它描述的函数是逆函数切线函数。将三角形的高度除以宽度在进行反正切即可求得角度。

 对称性

        当运行完FFT计算后，会注意到关于中心频率的对称，因为信号现在是离散的。也就是说只知道信号在哪里位于某些离散时间点。意味着拥有的信号仅存在于某些离散时间点。

        实例，通过采用DFT进行实验简单的2hz余弦波，该信号以16hz采样信号中有16个样本，因此DFT将测试16种不同的正弦波间隔为1Hz。测试的第一个正弦波为0Hz，1Hz，第三个2Hz以此类推一直向上至15Hz，对于每个频率测试信号用余弦波和反正弦波，将相乘后的结果绘制在标图上，计算分数查询每个频率与原始频率的匹配程度。使用勾股定理将余弦波的分数与正弦波的分数进行计算，计算后的结果再次绘制在新的一张标图上，如图7.2所示。对于第一个频率0Hz，余弦与正弦得到的分数都为零，重复过程1Hz会产生另一个零结果，当测试2Hz频率时候，余弦分数不为零，意味着2Hz是存在的频率在原始信号中，但是正弦分数依然为零，代表余弦分数是为原始信号在2Hz频率上贡献所有能量。以此类推测试剩余其他频率.......。当用14H波测试信号时候，余弦分数给出完全相同的分数，就像在测试2Hz频率时一样。

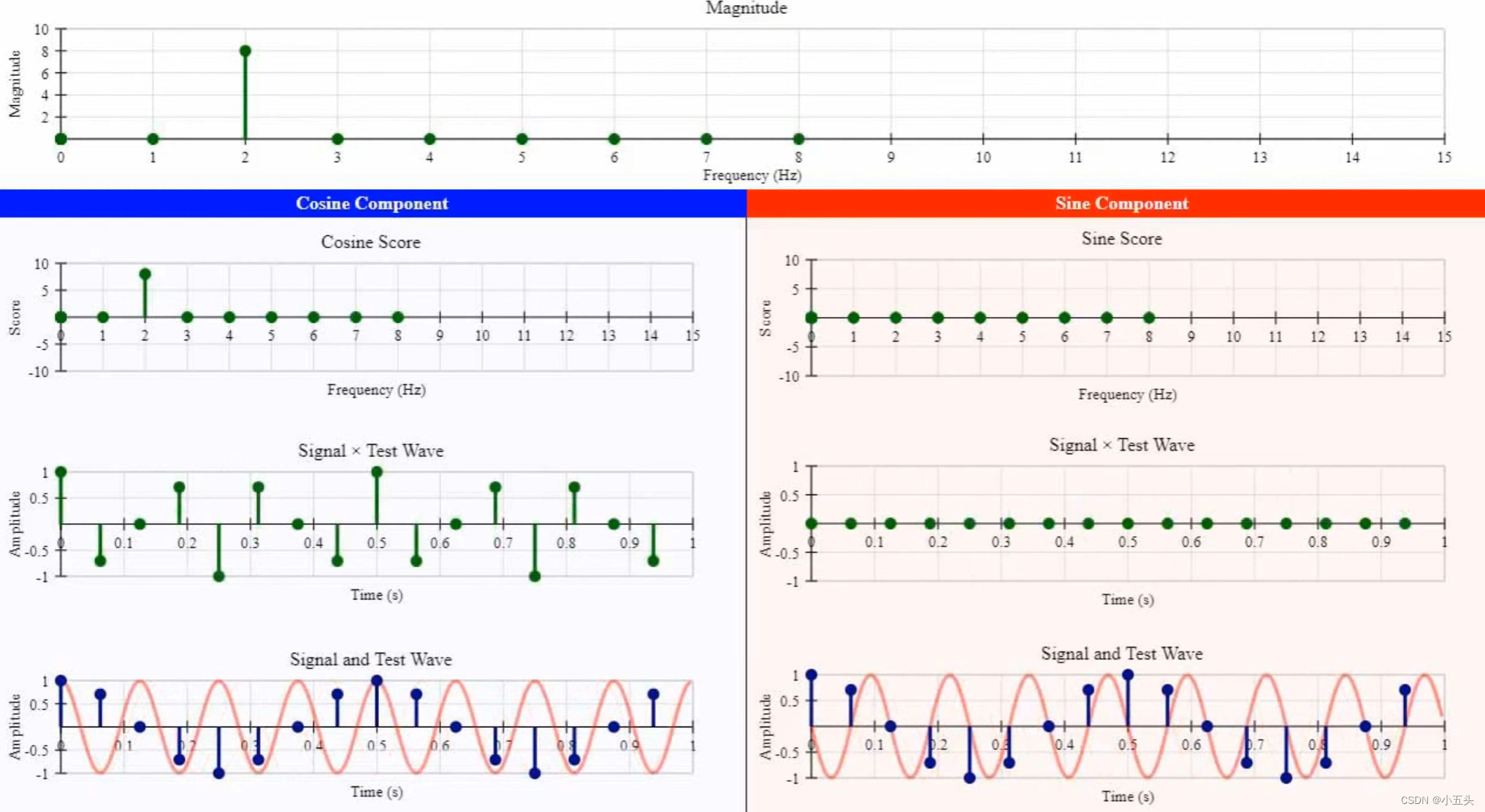
图7.2

        在14Hz时，测试波正好占据采样值与2hz测试波相同，关于两个波所能获取的信号就仅存在与采样点上，而巧合14Hz与2Hz的那些采样点重合。没对频率都会发生同样的事情中心频率约为8Hz，对于7Hz和9Hz频率也是如此等等......这就是为什么幅度输出的原因的FFT是对称的，中间的频率是一个非常特殊的频率称为奈奎斯特频率。

 DFT计算方法

        如图7.3所示。输入不同的K数据从0一直到N-1个，进行与测试波形进行乘积最后分别求和得出复数，输入不同的K得到不同的结果。为了让式子看起来更加简介对负指数项做个定义如图7.4所示。称为旋转因子：$W_N^k = e^{-j2\pi k/N}$，其中$N$为FFT长度，$k$为旋转因子的下标。旋转因子可以预先计算，并存储在一个数组中，以便在计算FFT时使用。在蝴蝶运算中，旋转因子的下标$k$与输入数据的下标$i$和$j$有关。将两者式子进行组合如图7.5所示。

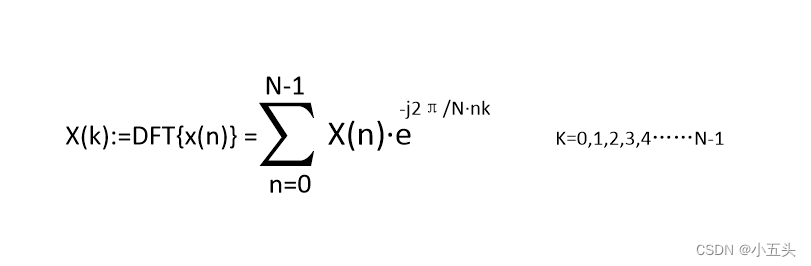
图7.3

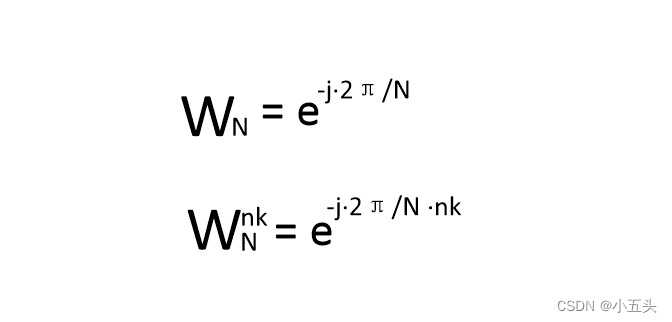图7.4

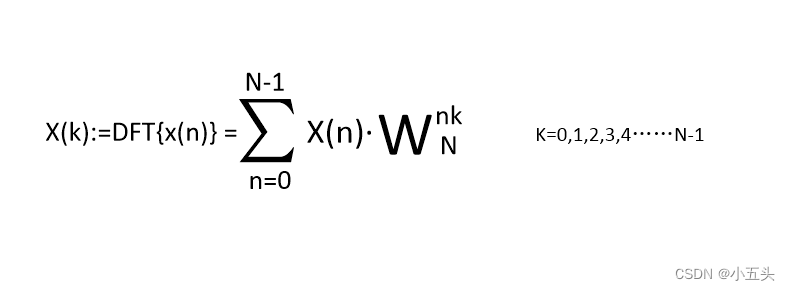
图7.5

        举例说明，取长度N=4的信号x(n),求得DFT结果，列式如图7.6所示。把K=0一直到K=3全部列出来如图7.7所示。将旋转因子提出来可以写成矩阵形式如图7.8所示，其中X为复数结果，x为输入的原始信号与旋转矩形相乘。

        1.原时间序列变为频率序列，每个点均对应一个频率分量；

        2.X(k)中每个点均为复数，X(k)与X(N-k)为共轭状态；

        3.摸值和相位代表当前点对应频率分量的幅度和相位（余弦函数形式）；

        4.有效频率分量为N/2个点，相邻点的频率间隔为F(s)/N。

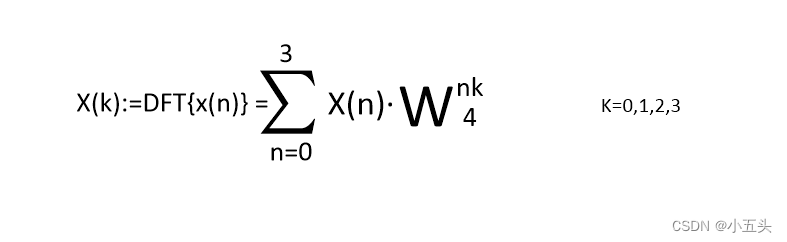
图7.6

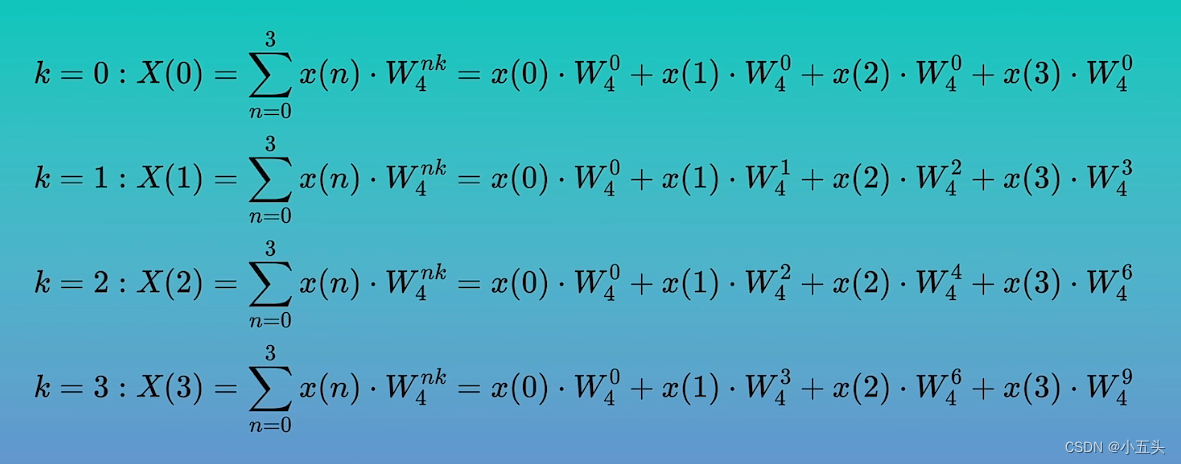
图7.7

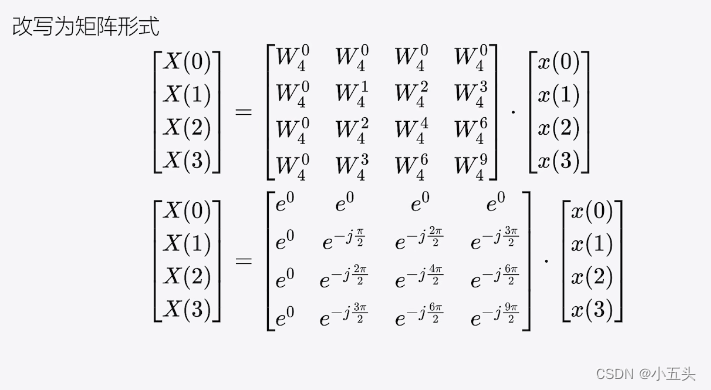
图7.8

        式列，信号为f(t)=cos(2π·3·t+π/3)，以16Hz频率采样，即3个信号周期采集16个点如图7.9所示。已知该信号频率3Hz，初始相位π/3，幅度为1。使用旋转因子矩阵乘以原始信号的点数等到复数结果如图8.0所示。因此采样了16个点所以N=16，则旋转因子为W下标16上标nk，则等于e^(-j2π/16)nk，图8.0则是将公共部分e^(-j2π/16)提出，在第一行K=0时，n从0-15变化取值相乘此行结果为直流信号（将所有的输入信号进行相加），以此类推最后一行k=15，n从0-15变化。计算结束后得到16个复数如图8.1所示。可以看到X(13)与X(3)是共轭的状态，则有效点数只有8个点。

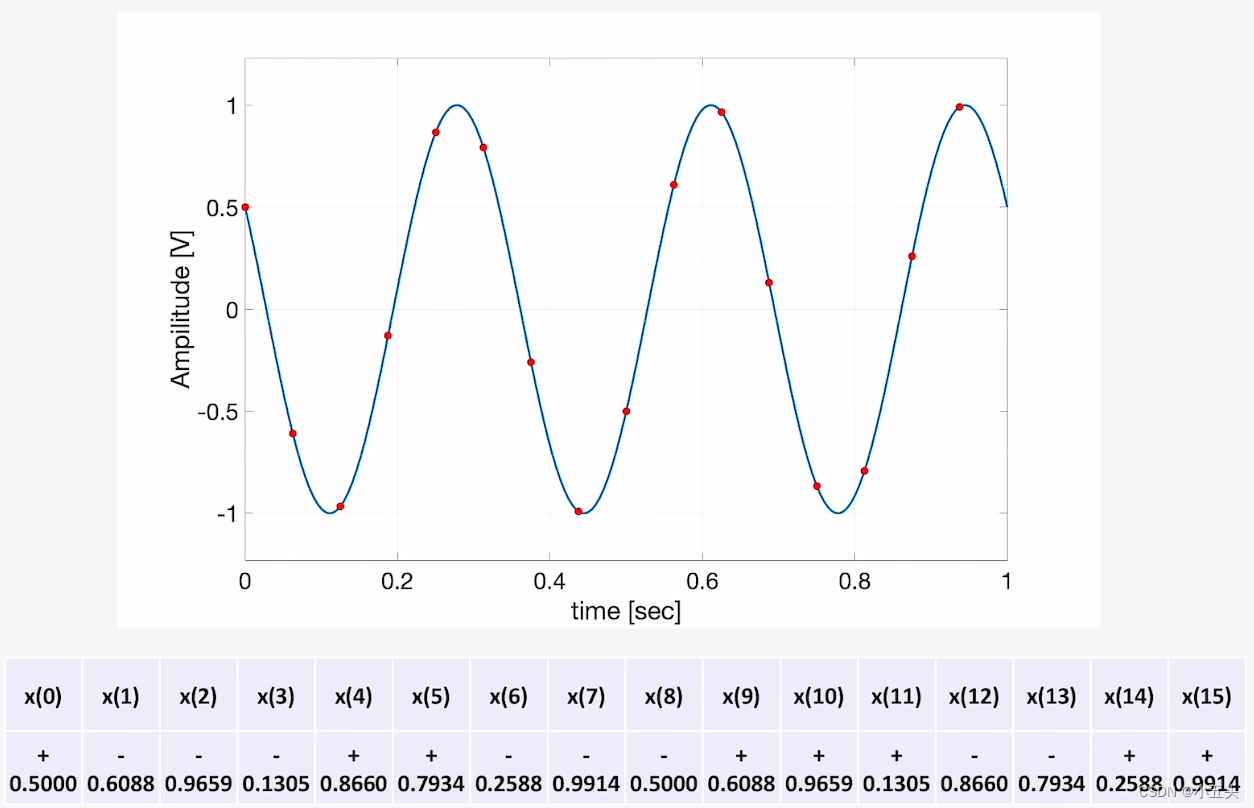
图7.9

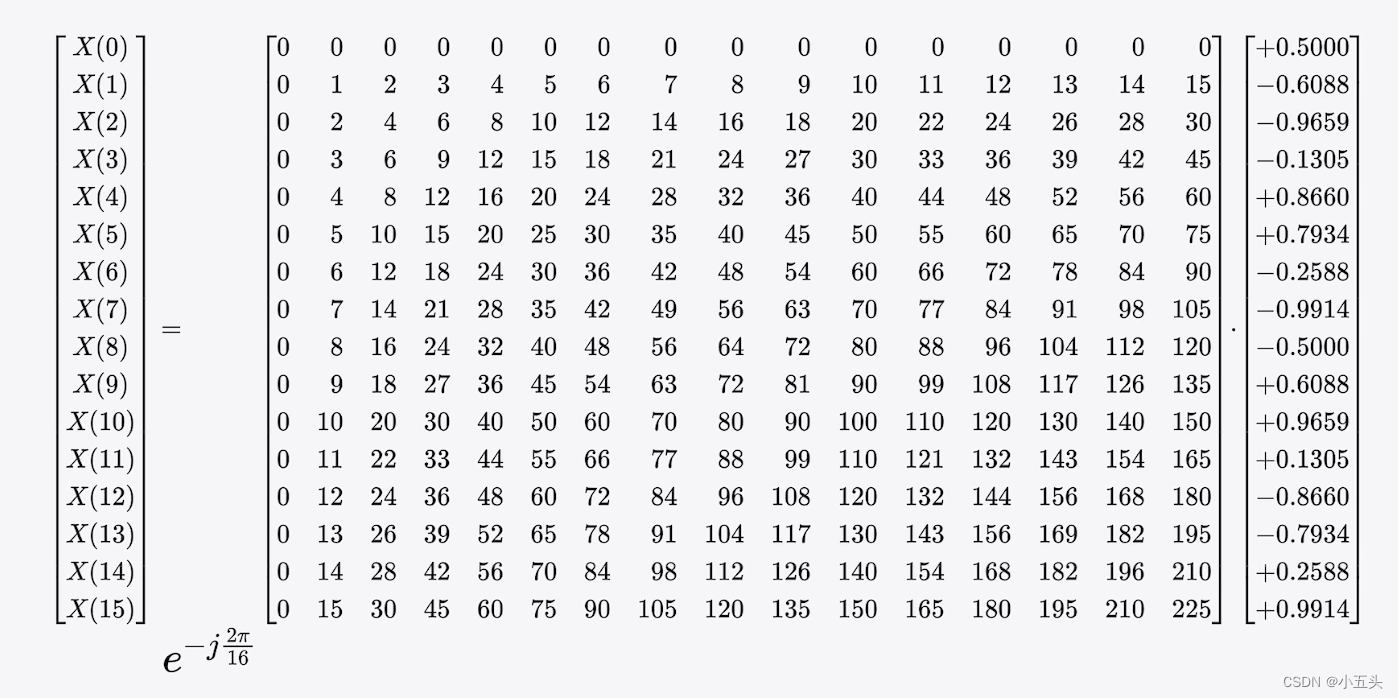
图8.0

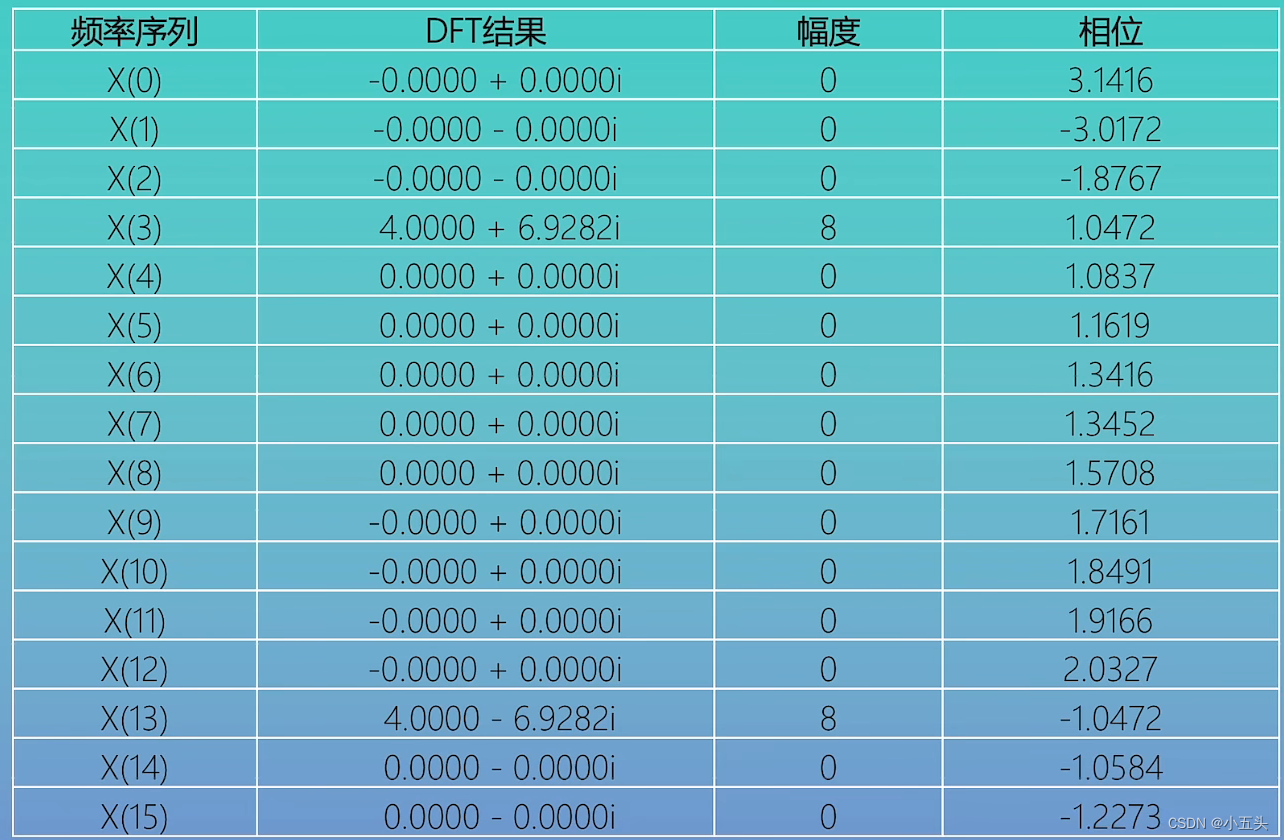
图8.1

  旋转因子

        以8个点单位圆为例如图8.2所示，一个复数的平面横坐标为实数轴，纵坐标为虚数轴，ω的取值位于圆上的这些点。将这些点中的数按照一定规格进行排布就变成了如图7.8那样的矩阵形式。用公式的方式表示如同图7.3其中∑e^(-i2Π/N·nk)可以用矩阵表达式，x[n]为原始信号，x[k]为每个相乘后得到的结果如图8.3。所描述的是一个基矩阵与一个原始向量相乘得到一个新向量。

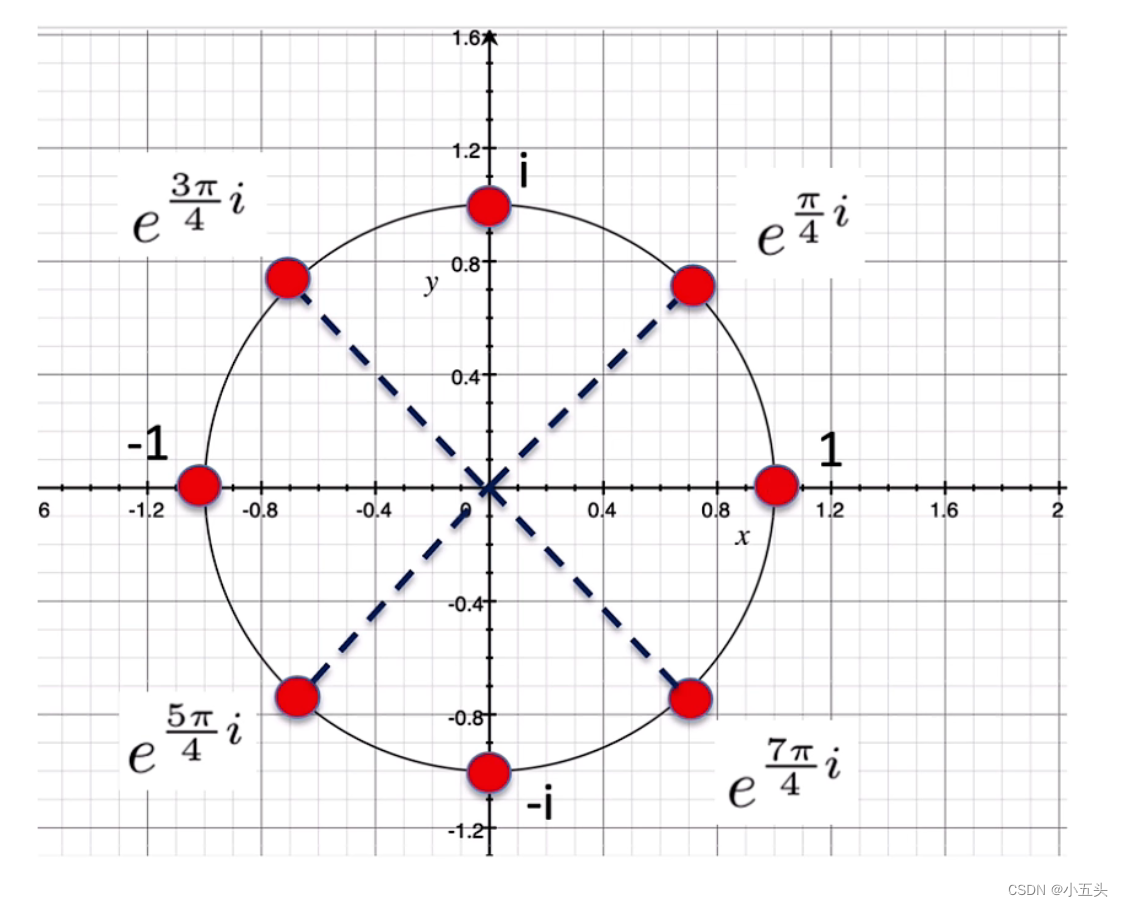
图8.2

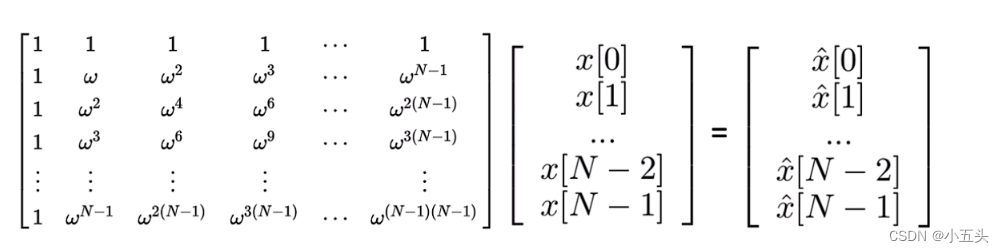
图8.3

  降低采样复杂度

        原始信号y=x^5+2x^4+x^3+x^2+x+0.2函数图像如图8.4所示，可以将多项式进行奇偶划分，但是会发现一个问题，多项式最高次的次数没有改变，导致划分后的多项式再次进行采点需要满足最高次的次数采点数还是一样多，所以需要对多项式进行将此操作，将X=X^2，那么整个式子的次数减半用同式表示如图8.5所示。

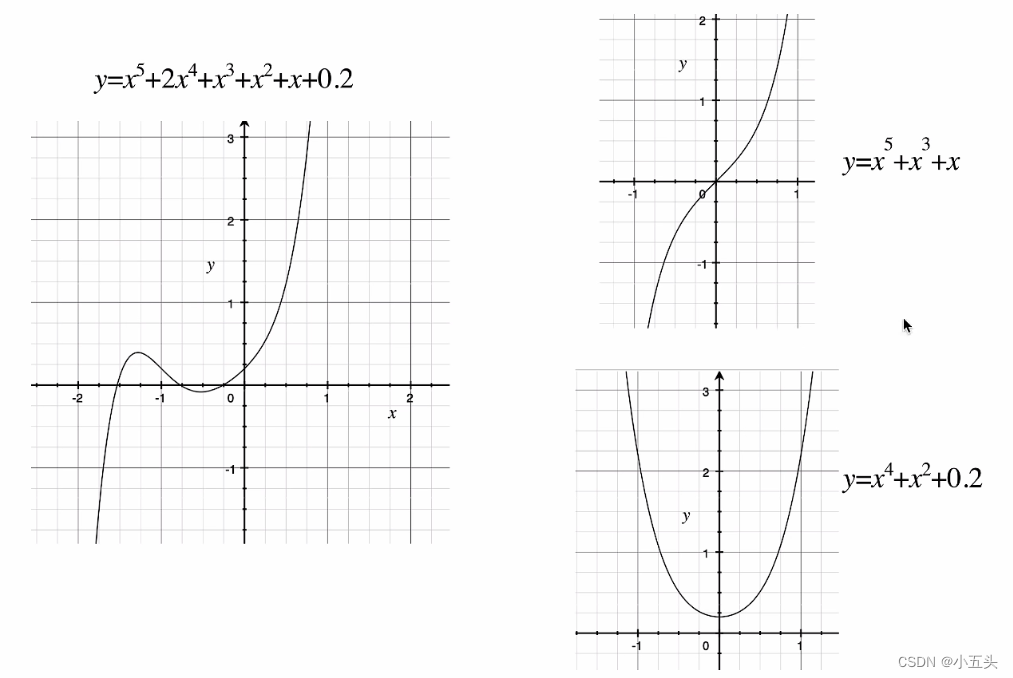
图8.4

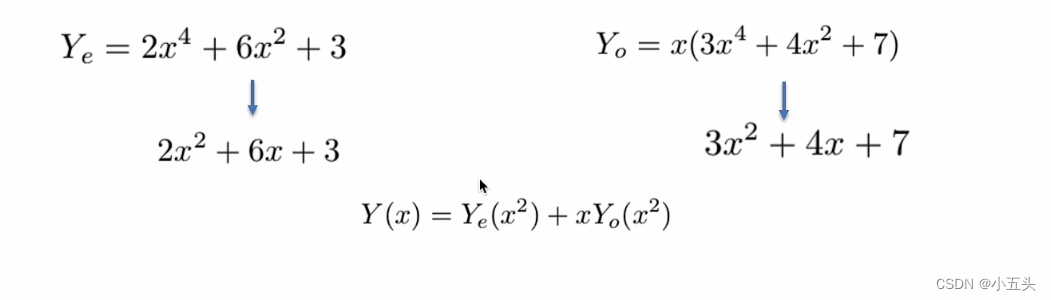
图8.5

   复共轭

        以一个简单的5Hz正弦曲线为例如图8.6所示，如果将它分解成它的余弦波和正弦波，它们都有5Hz的频率，但是它们的振幅不相同，当当它们加在一起时，它们会产生5Hz的正弦信号。如果对原始信号进行傅里叶变换将其转换为频域，余弦分量如图8.7所示，这是5Hz时的峰值在时域中余弦波振幅有0.8但是在频域中只有0.4，还有另一个-5Hz时相同振幅的峰值。频域状态下的正弦分量也是一样效果如图8.8所示。在5Hz频率幅度是一半但在-5Hz振幅为负时域振幅一半。在时域中余弦和正弦表示每个频率的分量，由一个复数余弦分量为实数部分，正弦分量为虚数部分。

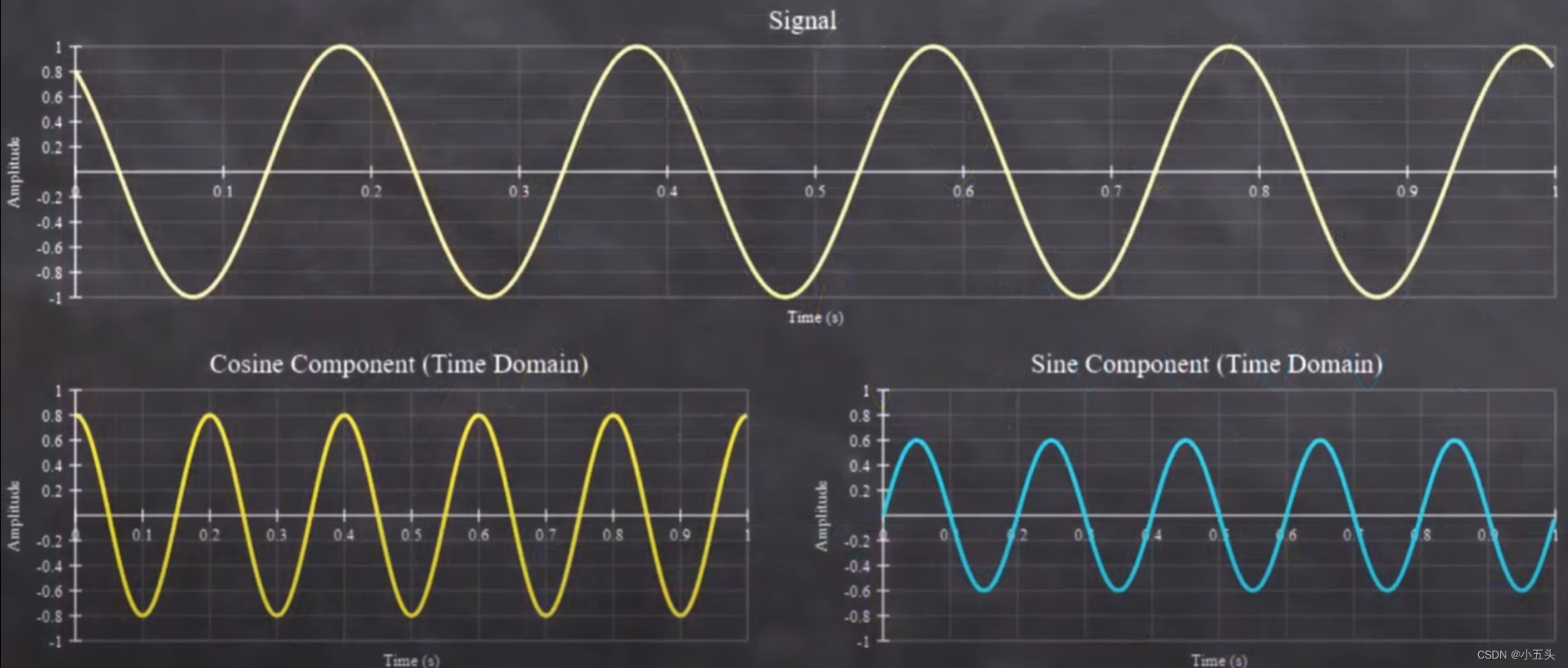
图8.6

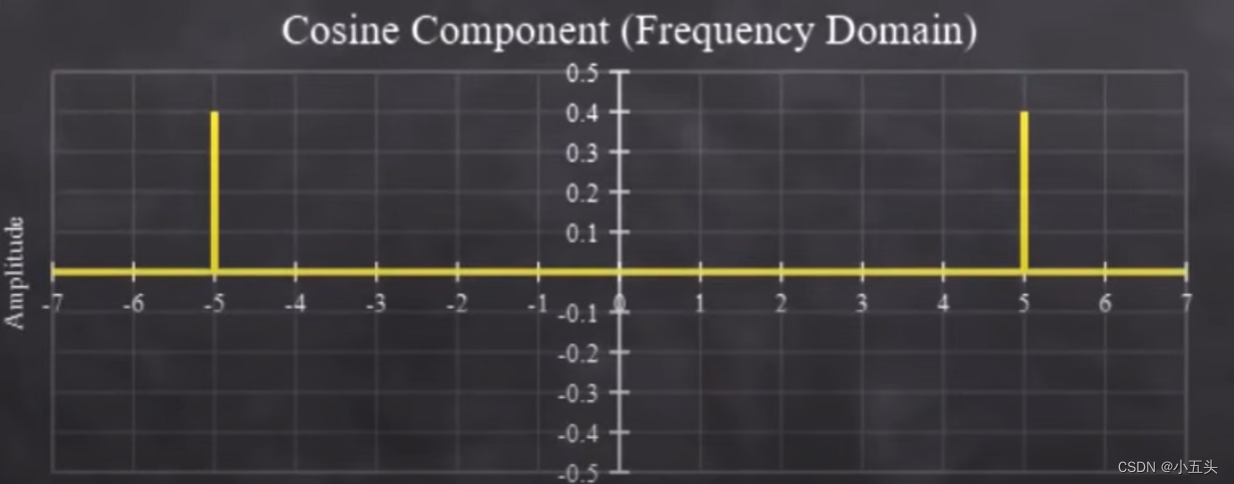
图8.7

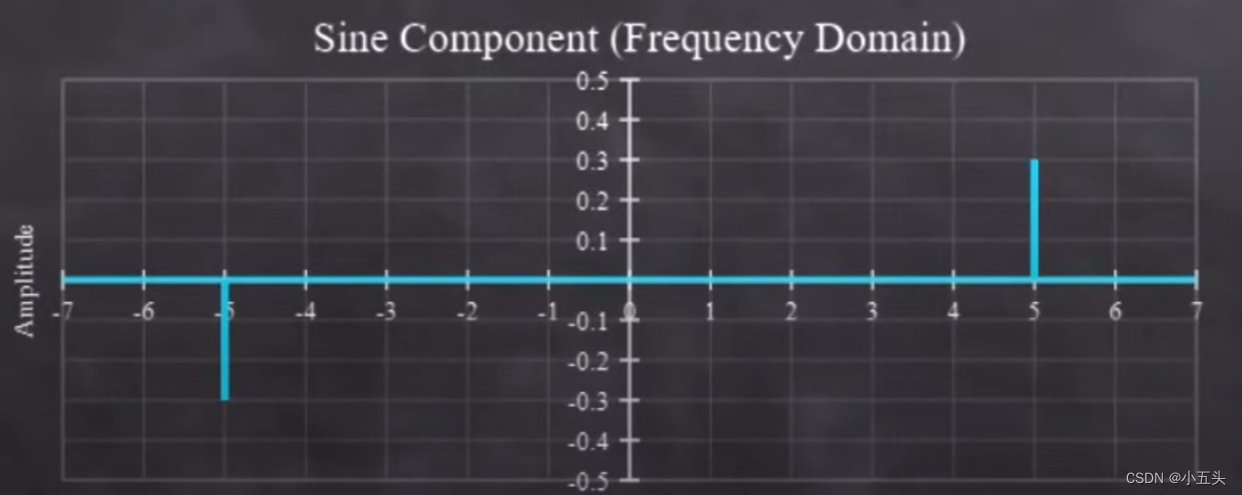
图8.8

        此信号中有两个非零频率，5Hz和-5Hz所以这个信号可以是由两个复数表示：其中5Hz表示为(0.4+0.3i)。其中-5Hz表示为(0.4-0.3i)，为了恢复信号从频域回到时域，则需要执行傅里叶逆运算，执行后会最终得到一个列表需要相加的复数，其中每个复数代表贡献信号的一个特定频率，这些数字中大多数将为零，保存正负5Hz频率因为它们是唯一的频率，存在与原始信号中如图8.9所示。把两个数字加在一起时，0.47i和-0.47i抵消了这意味着任何时刻的信号幅度，都可以用单个实数来描述。信号是真实的这就是为什么幅度谱任何真实信号的傅里叶变换总是沿着0Hz线反射以及为什么任何真实信号的相谱始终是，沿着0Hz反射并反转，因为如果不这样当加在一起时，虚构的部分不会抵消，并且时域信号不是真正的信号。

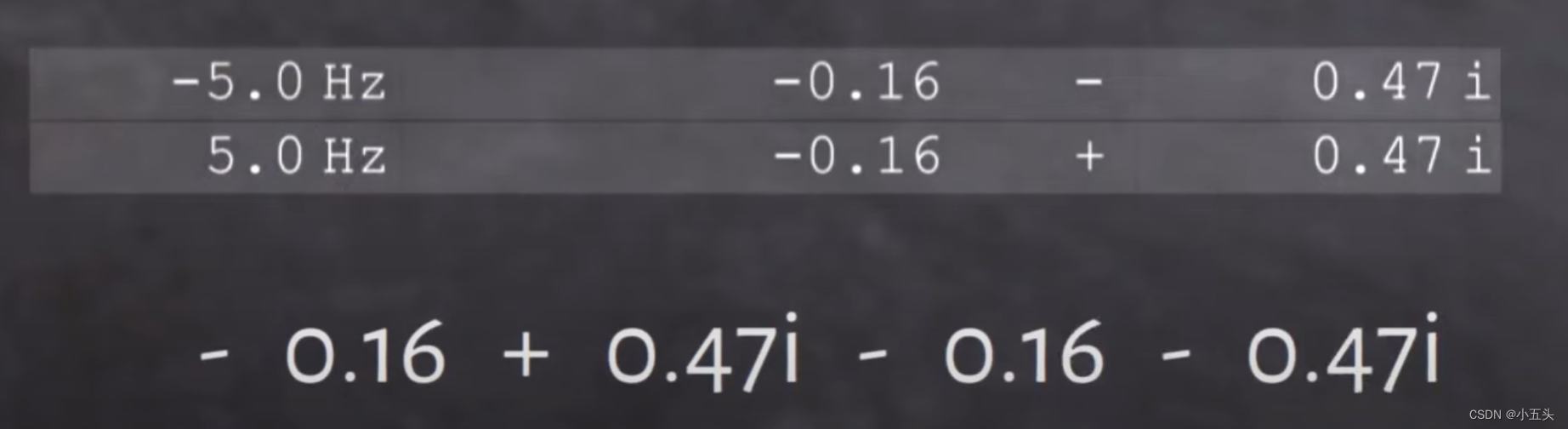
图8.9

  傅里叶逆变换

        Ω对我们考虑复平面时很有用，复平面组合余弦并将信号的正弦分量输入，一个二位坐标系X轴表示振幅任何时刻的余弦分量，Y轴表示振幅任何时刻的正弦分量。正弦波和余弦波的频率可以认为是旋转的速度，圆圈中间的一条线，这是这条线的角速度，如果使用Z轴绘制角度那么这条线然后圆就变成了一个螺旋如图9.0所示。生产线向上移动的速度Z轴是它的角速度，然而正如线条可以沿着Z轴向上移动一样，它也可以向相反的方向移动下。Z轴如果从两维角度看，这相当于以另一种方式旋转，当线沿Z轴向上移动是，其角度速度，或其频率为正，当线沿Z轴向下移动时，其角速度或其频率为负这就是负频率。

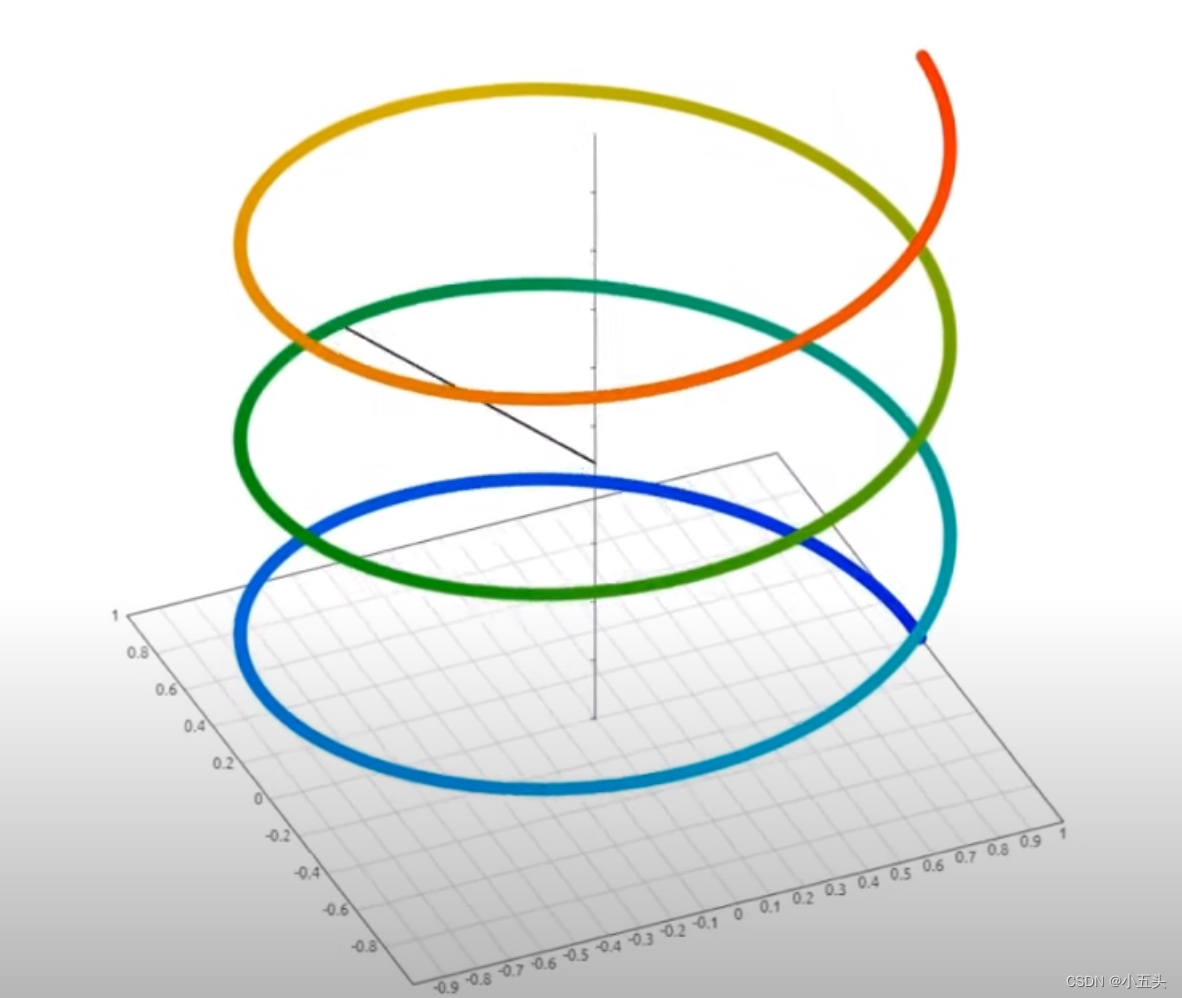
图9.0

        以图7.0举例，如果三角形以相反的方向旋转，那么余弦波看起来是一样的，单正弦图却是相反的，在正旋转期间现在为负，在负旋转期间反之亦然如图9.1所示。了解了其中的负频率就解释了为什么余弦的振幅在负5Hz的时候依然是正的。以及为什么正弦波的振幅在负5Hz的时候分量为负。

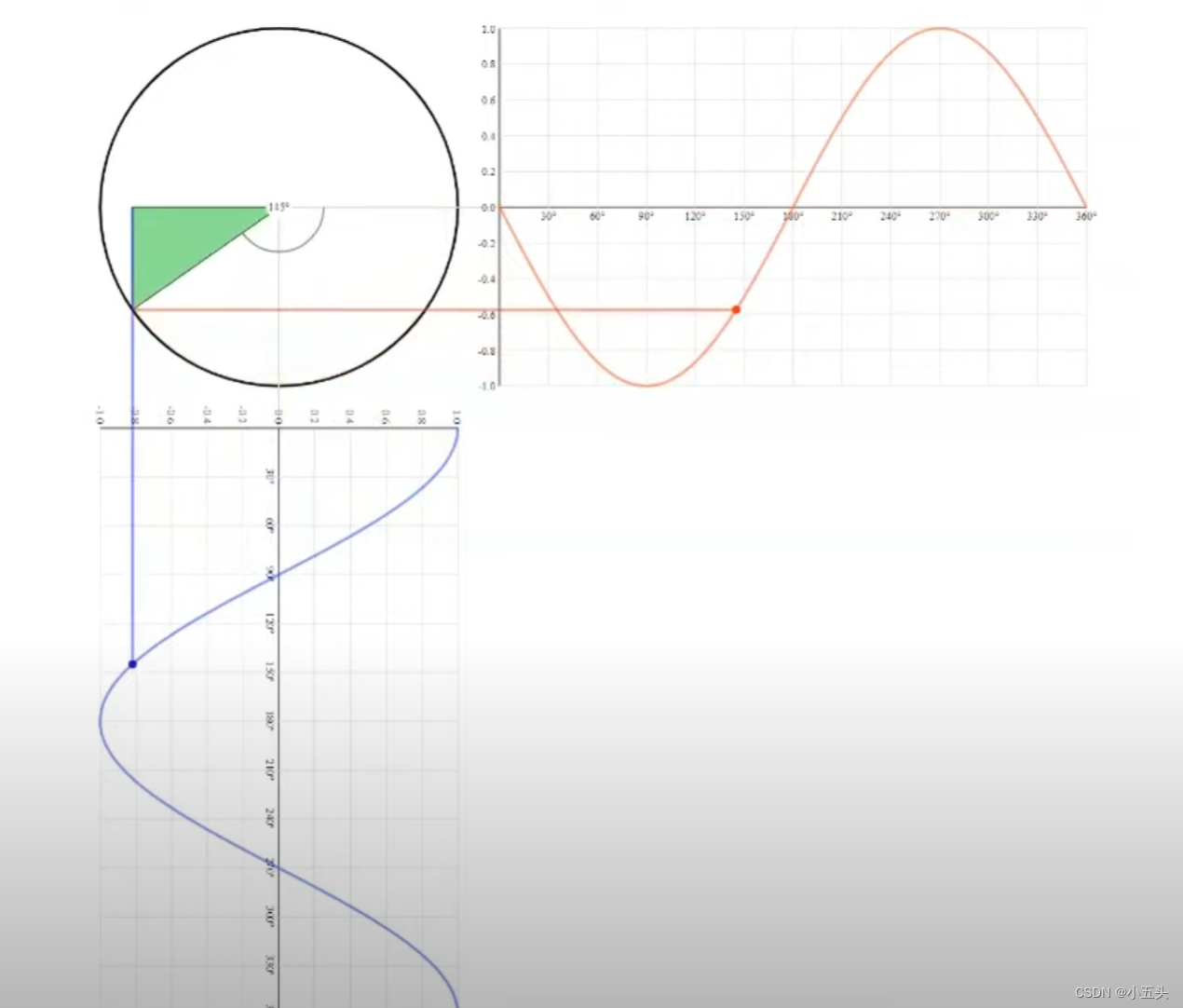
图9.1

        如果想恢复信号需要利用傅里叶立方体如图9.2所示，可以帮助我们快速理解傅里叶逆变换，我们的信号在傅里叶变换中信号向下进入其组成正弦波，而傅里叶逆变换恰恰相反，将所有正弦曲线重新组合在一起以恢复原始时域信号。在不同频率下相加恢复原始信号，首先需要从余弦分量和正弦分量中恢复成正弦波和余弦波，公式表达如图9.3所示。其中X(f)是复数的列表表示振幅各种余弦分量与正弦分量频率，每个复数乘以余弦波和正弦波在该频率下。但是两个复数相乘不足以恢复成我们需要正弦波和余弦波，因为乘法的结果依然包含一个虚部，非常复杂看起来像三维螺旋。

图9.2

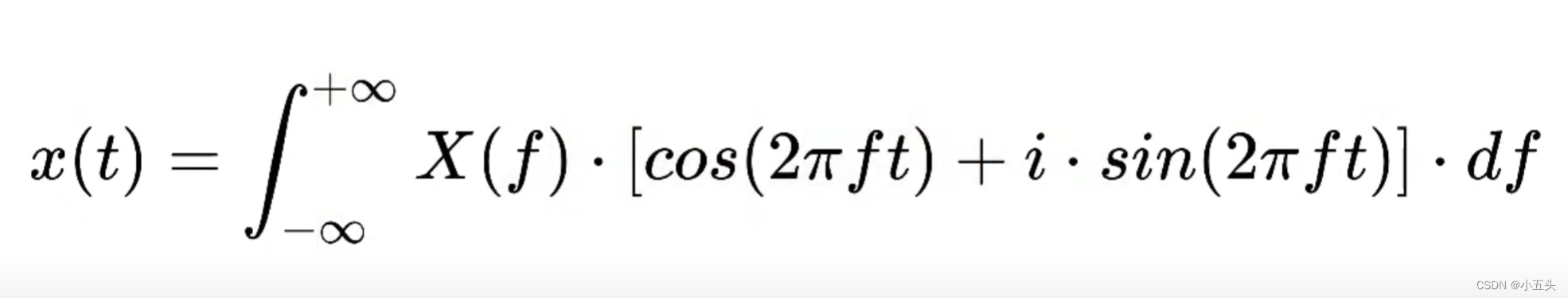
图9.3

        逆向的最后阶段傅里叶变换需要加法，将所有复杂的正弦曲线相加在一起，复数的正弦分量负频率与正弦分量完全相反对应的正频率，将它们相加在一起时虚轴的正弦分量相减低，只留下了一个真正的正弦波。所以这就是负频率为什么存在于我们的信号中，它的存在是为了确定虚部傅里叶变换后进行逆变换。

  FFT

        回顾离散傅里叶DFT公式如图9.4所示，从第一个式子可以看到在进行每一个点的DFT运算的时候，要将e和-j^(2π/N)nk进行相乘在相加才能得到X(k)的结果。每一点的X(k)的值需要进行N次相乘和N-1次的复数相加，这样才能得到1个点的X(k)的值。要完成全部DFT运算需要进行N^2次复数乘法和N(N-1)次复数加法。

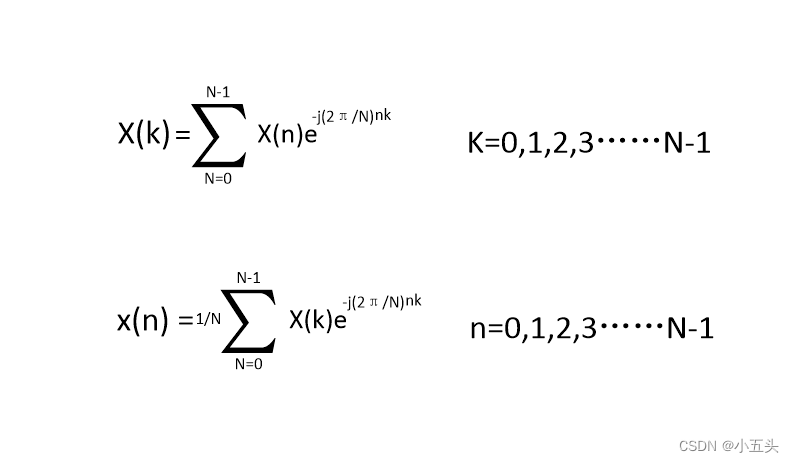
图9.4

        为了提高运算速度，先从公式进行改进，为了方便计算将-j^(2π/N)带指数的表达为W^nk,将X(K)和x(n)之间用矩阵的形式来表达如图9.5所示。为了更加简化运算前辈了研究出W^nk两大特点周期性和对称性。

        1.W^nk周期性：具体来说，周期性函数W^nk的周期为2π/n。也就是说，在每个2π/n的间隔内，函数W^nk会重复其值。这意味着，如果你将W^nk的自变量（通常是角度）增加2π/n，函数的值将再次与初始值相等。但是需要注意的是，周期性函数W^nk的周期与n的取值有关。不同的n将导致不同的周期长度。例如，当n=1时，W^nk的周期为2π；当n=2时，W^nk的周期为π；当n=3时，W^nk的周期为2π/3，依此类推。

        2.W^nk对称性：对于k = 0, 1, 2, …, n-1，W^nk中的每个元素都是复数单位模的n次根。因此，W^nk在固定的k值下具有周期性对称性，即当k增加n倍时，W^nk保持不变。当n为偶数时，W^nk中的元素具有共轭对称性。具体地说，当k取值为k1和k2时，W^nk1中的每个元素与W^nk2中对应位置的元素互为共轭。

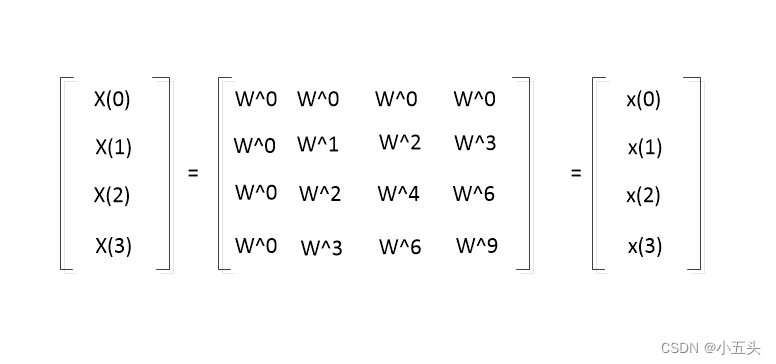
图9.5

        因为再W矩阵中存在这很多不必要的重复运算，所以这两大特点用在W的矩阵中。将N点DFT运算分解成两组N/2点的DFT运算，然后取和。假设N是2的整数次方，将公式分成两个部分一部分是偶数数列，一部分是奇数序列。用(2r)表示偶数数列(2r-1)表示奇数序列如图9.6所示。

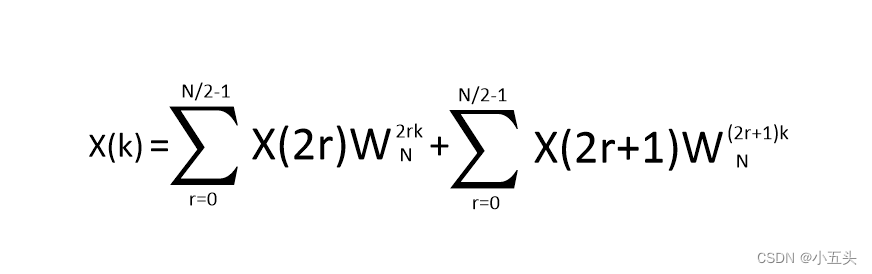
图9.6

        实列，以N=2^2=4为列的DFT的运算进行说明，公式如图9.7所示。根据此表达式可以列出每个K值时候的式子如图9.8所示。化作为矩阵形式如图图9.5所示，首先根据W的周期序列长度为N的W的0次幂等于1，序列长度为N的W的mN次幂等于1换算后如图9.9所示。在根据对称性序列长度为N的mN+N/2次幂等于-1简化后的矩阵如图10.1所示。再次根据对称性N的r+N/2等于-W的r次幂。

如图10.2所示。

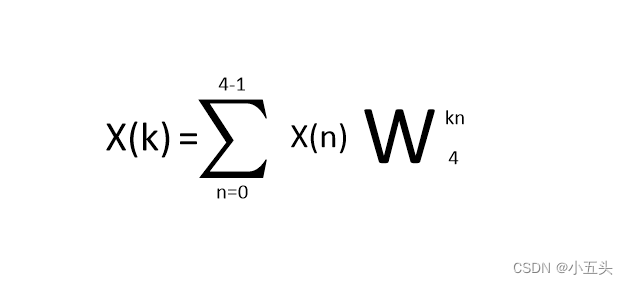
图9.7

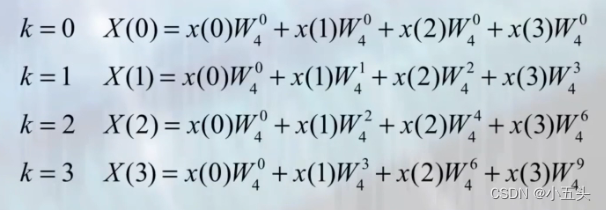
图9.8

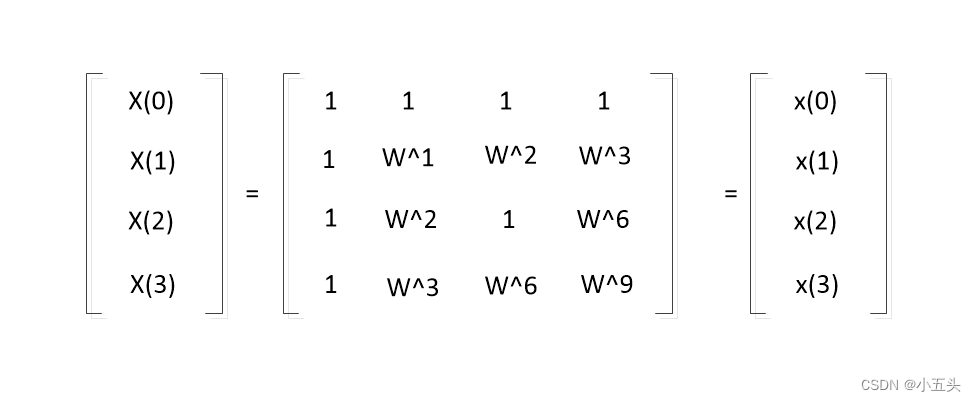
图9.9

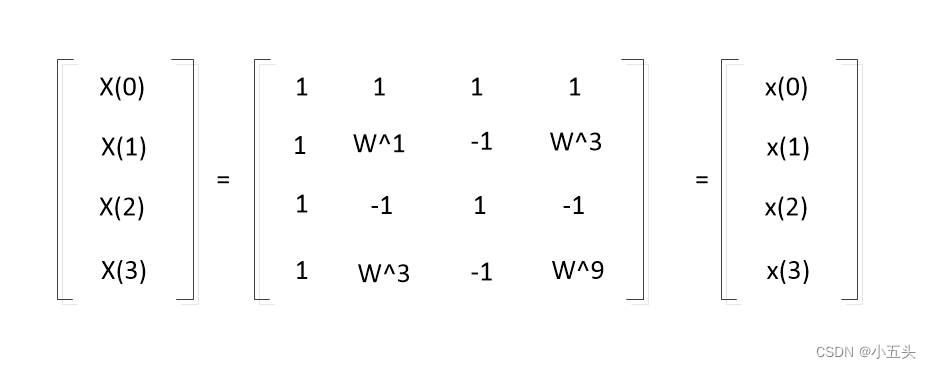
图10.1

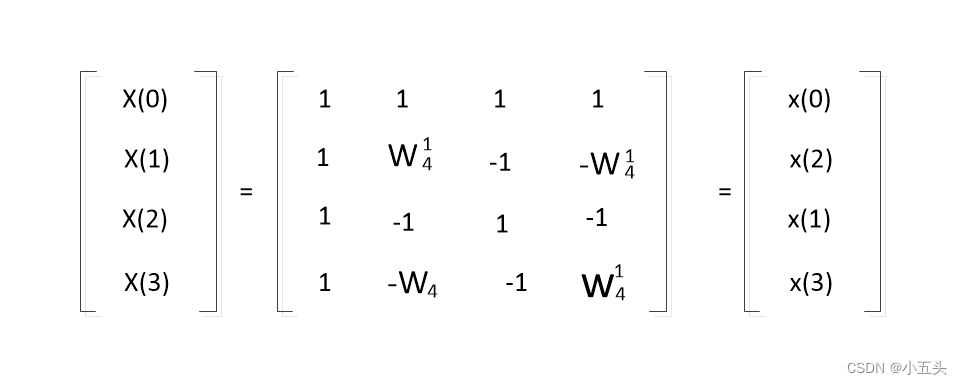
图10.2

        将矩阵式子的，第二行和第三行互换，第二列和第三列互换，x(1)和x(2)互换矩阵等式不变如图10.3所示。使用红色线将W矩阵分成4个小矩阵，左边上下完全相等的矩阵只和x(0)，x(2)有关，而右边的两列只和x(1)，x(3)有关并成相反的关系。与x(0)，x(1)，x(2)，x(3)对应相乘得出每一项的DFT结果如图10.4所示，列出后可以发现很多相同的项，比如X(0)和X(2)它们的前两项都是x(0)+x(2)此项可以定义为G(0)，它们的后两项都有一个共同的x(1)+x(3)可以定义为H(0)。再次观察在X(1)和X(3)时，将前两项相同值x(0)-x(2)定义为G(1),后两项相同的x(1)-x(3)定义为H(1)。定义后如图10.5所示。

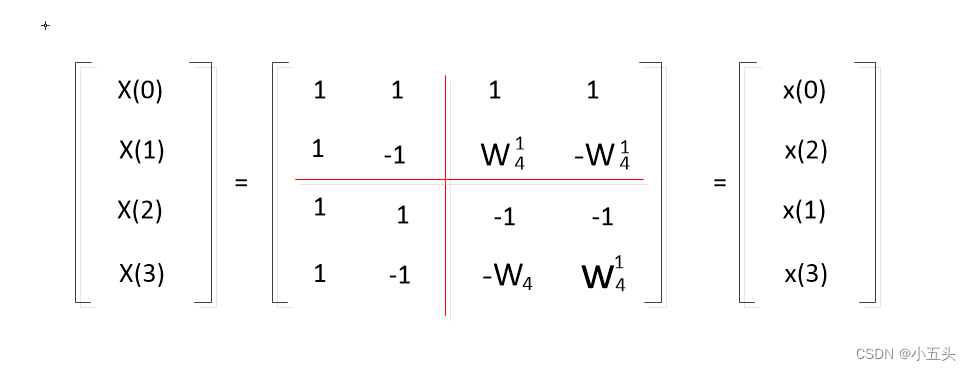
图10.3

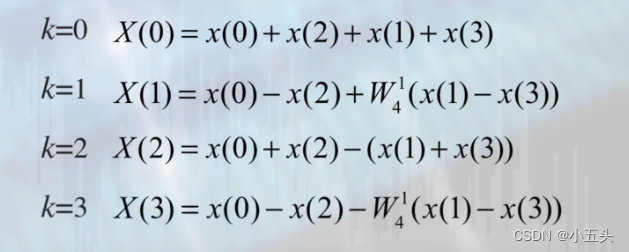
图10.4

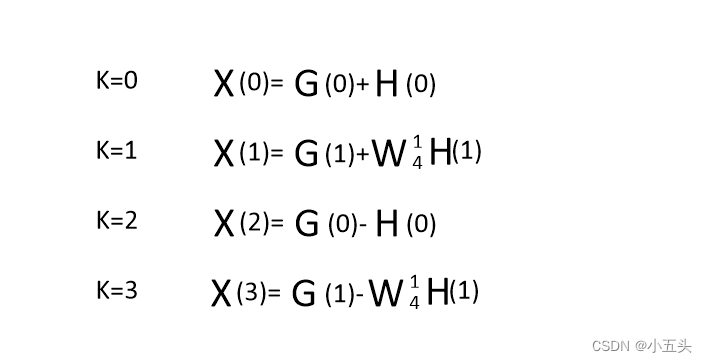
图10.5

        写成这种形式，计算量得到了大大的提升，因为其中G(0)，G(1),H(0),H(1)是通过四次加法得到的，X(0)，X(1)，X(2)，X(3)通过一次加法就得到了最终的结果。实际在进行这样的计算中加法通过8次，乘法通过4次就把结果得出。

        总结一下N点的快速计算方法，首先将N点的DFT运算分解成两组N/2点的DFT运算然后取和。通过图9.6可以继续延续分解，已分解成偶数n和奇数n相加。将N点写成N/2点如图10.6所示。将偶数部分定位G(k)，将奇数部分定义成H(k)则最后的公式简为如图10.7所示。其中G(k)相当于N/2点的DFT，H(k)相当于N/2点的DFT。

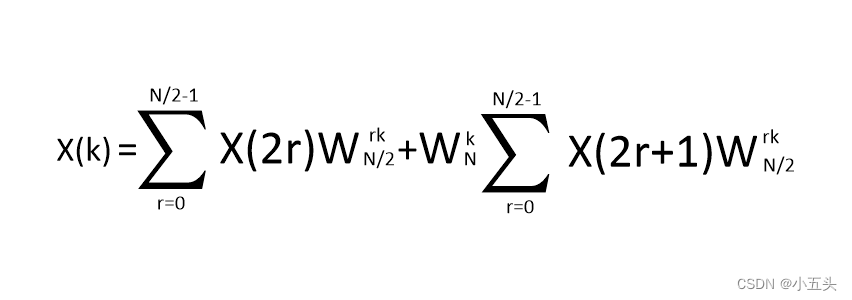
图10.6

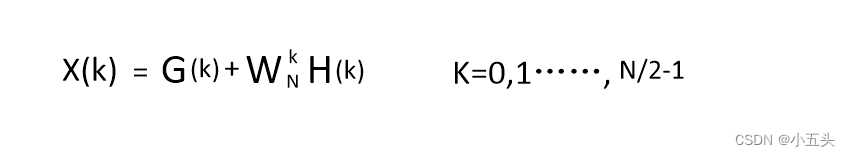
图10.7

        如果用G(k)和H(k)来表达全部的X(k)，那么应该并用G(k)和H(k)的两个重复的周期。由周期性可知G(k+N/2)=G(k),H(k+N/2)=H(k)，在利用加权系数Wn的特点，序列长度为N的k+N/2等于Wn的N/2乘Wn的k也就等于-Wn的k。将这些表达式代入前面的X(k)的计算中可以由G(k)和H(k)来决定X(k)的全部关系式。

        在图10.7中已得出公式，那么根据对称性X(k+N/2)等于G(k)-Wn的k乘以H(k)如图10.8所示，其中X(k+N/2)就是另外主值周期还有N/2点的X(k)。如果是4点的话那么只要k=2 X(2)=G(0)-H(0)和 k=3 X(3) = G(1) - W4的1乘以H(1)就可以计算出来了。

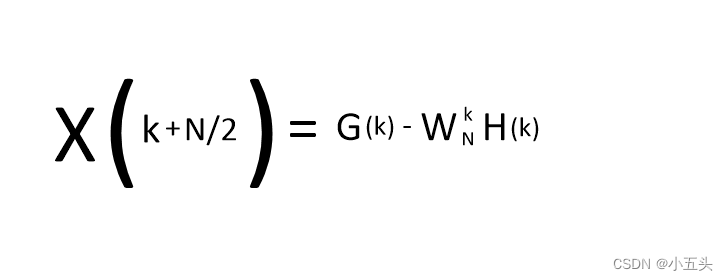
图10.8

  蝶形运算

        在N=4为例DFT分组的实际情况如图10.9所示，x(0)和x(2)分在偶数组，x(1)和x(3)分在奇数组，计算的结果又混在了一起了然后进行N点的DFT。

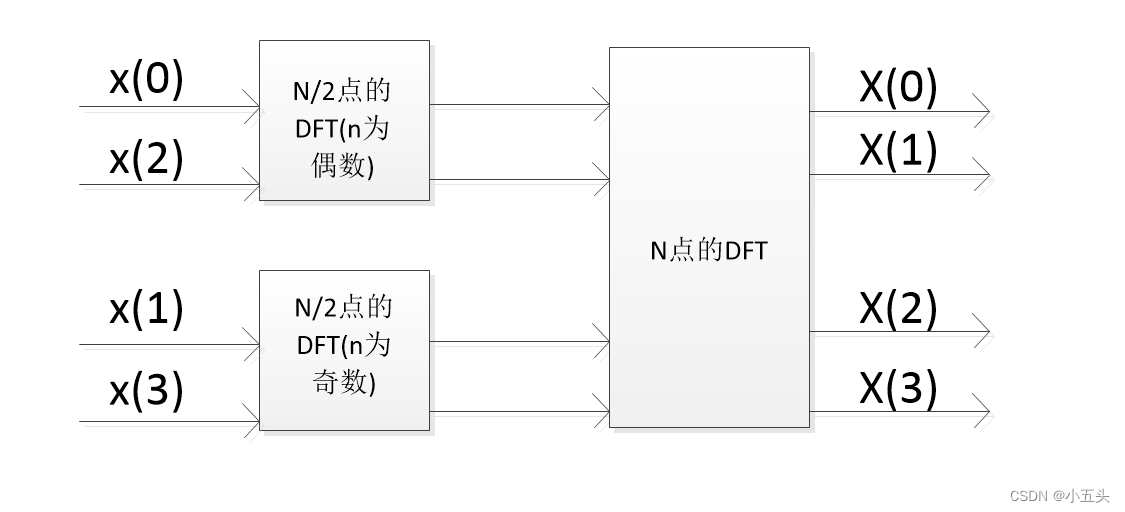
图10.9

        也可以使用蝴蝶图在描述计算过程，两条线的汇合点是表示两个数值的相加，线旁边标注的W是与复数做乘法的运算如图11.1所示。此蝴蝶运算图包括两次乘法和两次加法，以此类推将x(1)和x(3)全部描述出来。然而计算X(0)和X(2)也同样需要两次加法和两次乘法如图11.2所示。

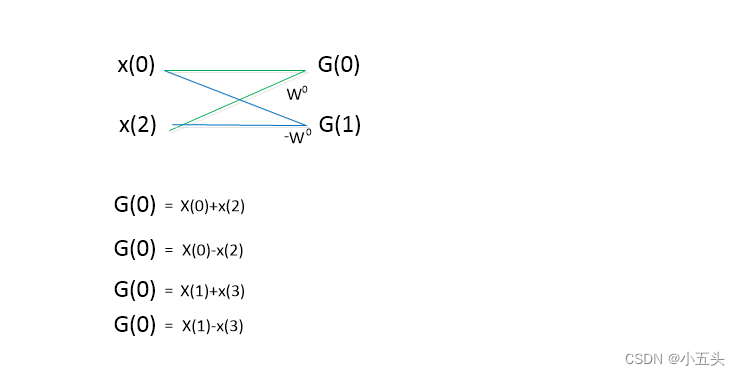
图11.1

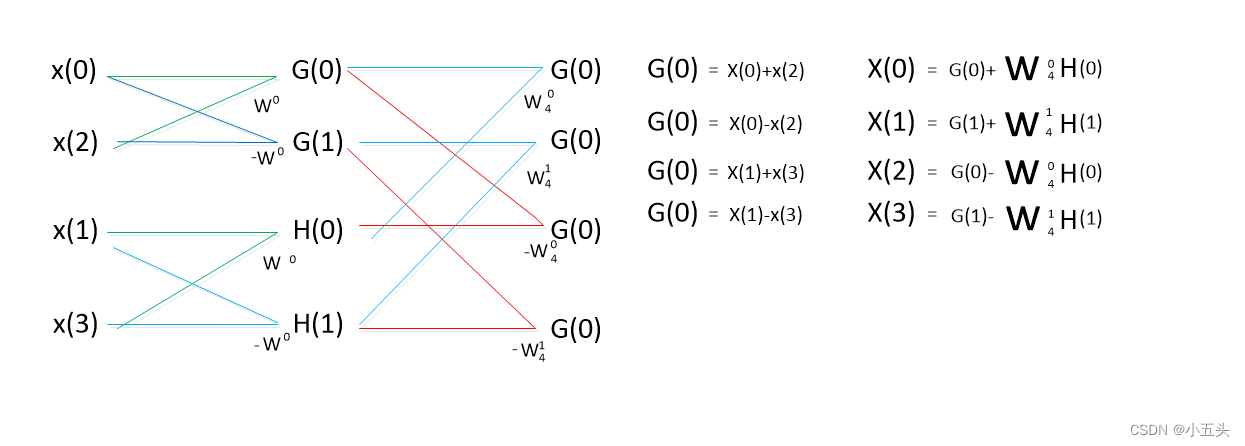
图11.2

        此蝶形运算中有些地方重发可以进行简化处理。H(0)乘以W4的0和-W4的0，可以改写成H(0)和W4的0相乘然后在分别相加分别相减，这样可以使运算量减少到只有一次复数乘法，和两次复数加法。那么就可以简化为如图11.3所示。因此就能得到这样的结论G(k)和H(k)获得的X(k)的过程中，可以看到的蝶形单元两个也就是N/8个运算单元，每个新单元进行一次复数乘法和两次复数加减法，因此也就是需要进行N/2的复数乘法和N此的复数加减法。

图11.3

        左半边是按N的奇偶分别组合了两个N/2点的DFT的运算，也是分成了两个蝶形单元，这个两个蝶形单元的运算量也还是N/2的复数乘法和N此的复数加法。对于4次的这种只在左半边进行了奇偶分解。比如但N=8的时候逐级分解为两个N/2点，四个N/2点的DFT运算如图11.4所示。

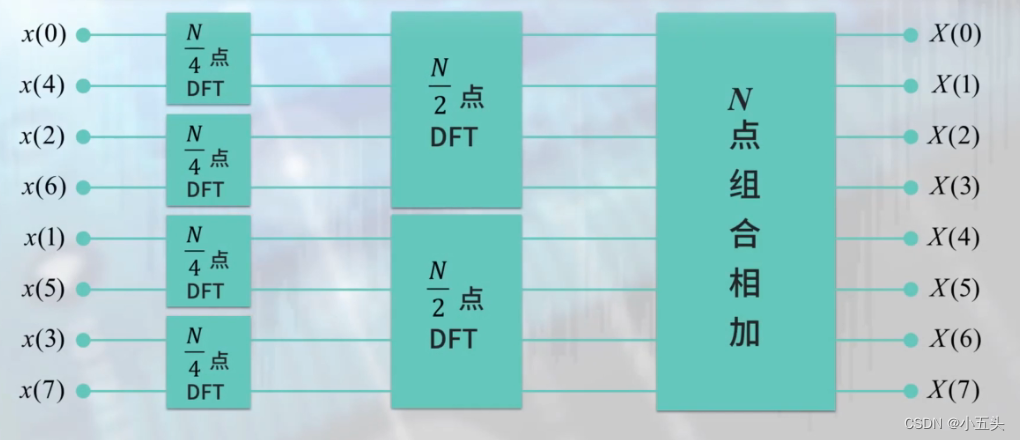
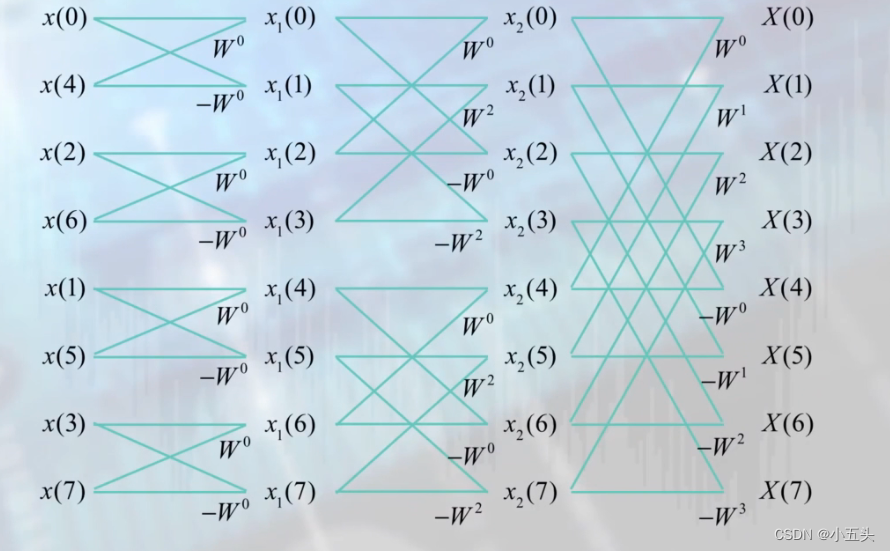
图11.4

        FFT算法特点，基本运算单元为一个蝶形，第M级的蝶形如图11.5所示，前一块的入端有上节点和下节点，那么出端同样也有上节点和下节点。入的上节点与下节点相加减，最后得到出端的上节点和下节点，这样就构成了基本的蝶形单元。

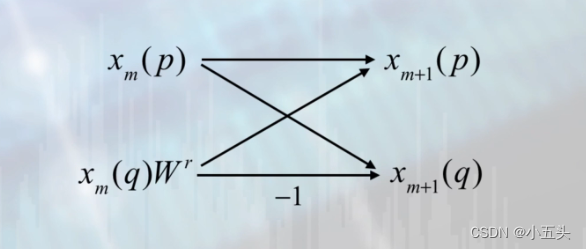
图11.5

        每一个蝶形单元都是独立的，而每一级有N/2个蝶形，在图11.4中在最左则和中则还有最右则中分别有四个蝶形。那么在N=2^n的任意情况有M级的蝶形，在每一级里可以分成N/2^i组。每个蝶形单元仅需一次复数乘法，两次复数加法就可以得到输出端如图11.6所示，这两点构成了一个蝶形单元，并且这俩点不再参与别的蝶形单元的运算。

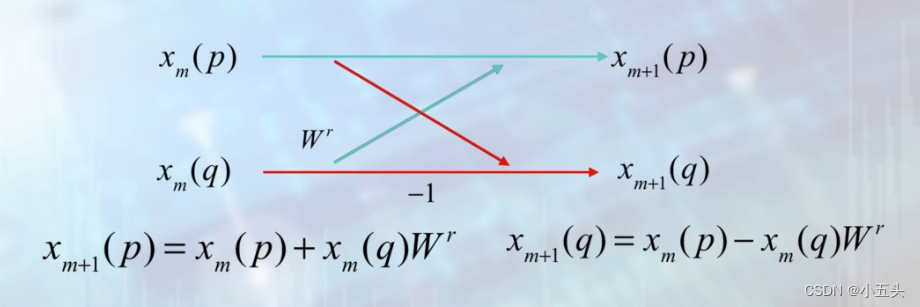
图11.6

        还有一个特点在进行快速傅里叶变换时，进行了一个码位的倒置，输入如果是岛序的话则输出是正序，因为在进行矩阵变换的时候在N=4点的运算过程中，将第二行和第三行进行了互换则相应的就把第二列和第三列也进行了互换。所最后得到的DFT的结果可以按二进制排序，输入二进制而输出则是二进制的码位倒置如图11.7所示。

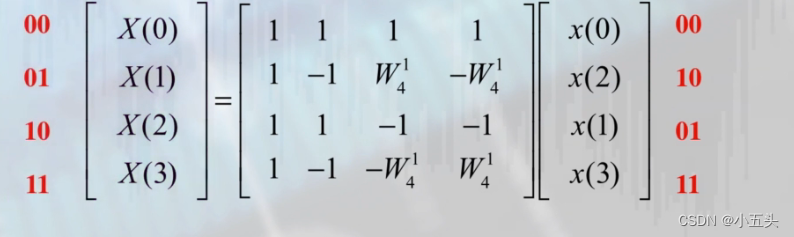
图11.7

        逆变换IFFT可以用同一个公式，只需某个形式参量代入不同的实际值如图11.8所示，它们的差别只在于W的-nk还有运算的结果要乘以1/N。在应用FFT中还需一些注意事项：

        1.信号离散时，采样率要攒足奈奎斯特频率。

        2.N一定是2的正数词幂，若不是，要补若干个零，凑成2的正数次幂。

        3.数据长度要取得足够长▲f=1/NT。其中▲f为频率分辨率。NT是数据的实际长度，N是序列的点数，Ts是采样周期。

 

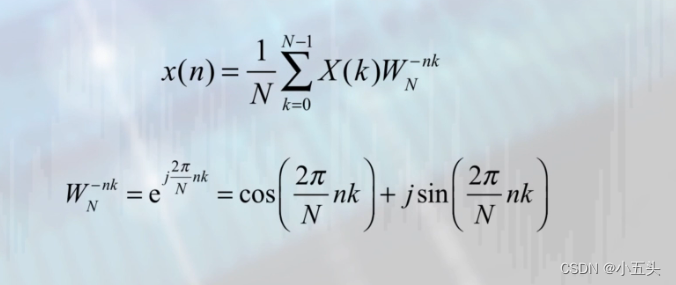
图11.8

 FPGA实现

  实验说明

        假设信号频率为F，采样频率为Fs，采样点数为N：那么FFT之后结果就是N个复数，每一个复数对应着一个频率点，频率间隔(分辨率)为Fs/N，第一个点表示直流分量(频率为0Hz)，第N个点的频率为Fn=(n-1)*Fs/N;

        各频率点下复数的模值，就是该频率下正弦信号的幅度特性，FFT结果具有对称性，通常我们只使用前半部的结果。设Xn=[4  3  2  6  7 8  9  0]；经过FFT后得：

        39.0000   -10.7782+6.2929i   0-5.0000i   4.7782-7.7071i   

        5.0000      4.7782+7.7071i   0+5.0000i   -10.7782-6.2929i

        假设采样频率为48KHz，那么两个频点之间的间隔48/8=6Khz。第一个为直流分量0Hz，第二个点为6Khz，第二个点频率为12KHz以此类推。对于中间点两边的值实部相等虚部相反称为共轭对称，但是它们的模值相等也就是幅度相等，反映在频谱上的效果就是会出现两个高度相同的脉冲并对称的。

  实验实现

        时序图如图11.9所示。当source_sop拉高表示一帧数据开始，source_eop表示一帧数据结束。sink_real 数据的实部，sink_imag数据的虚部。source_real和source_imag同样为输出后结果的实部和虚部数据，当source_valid拉高时候数据有效。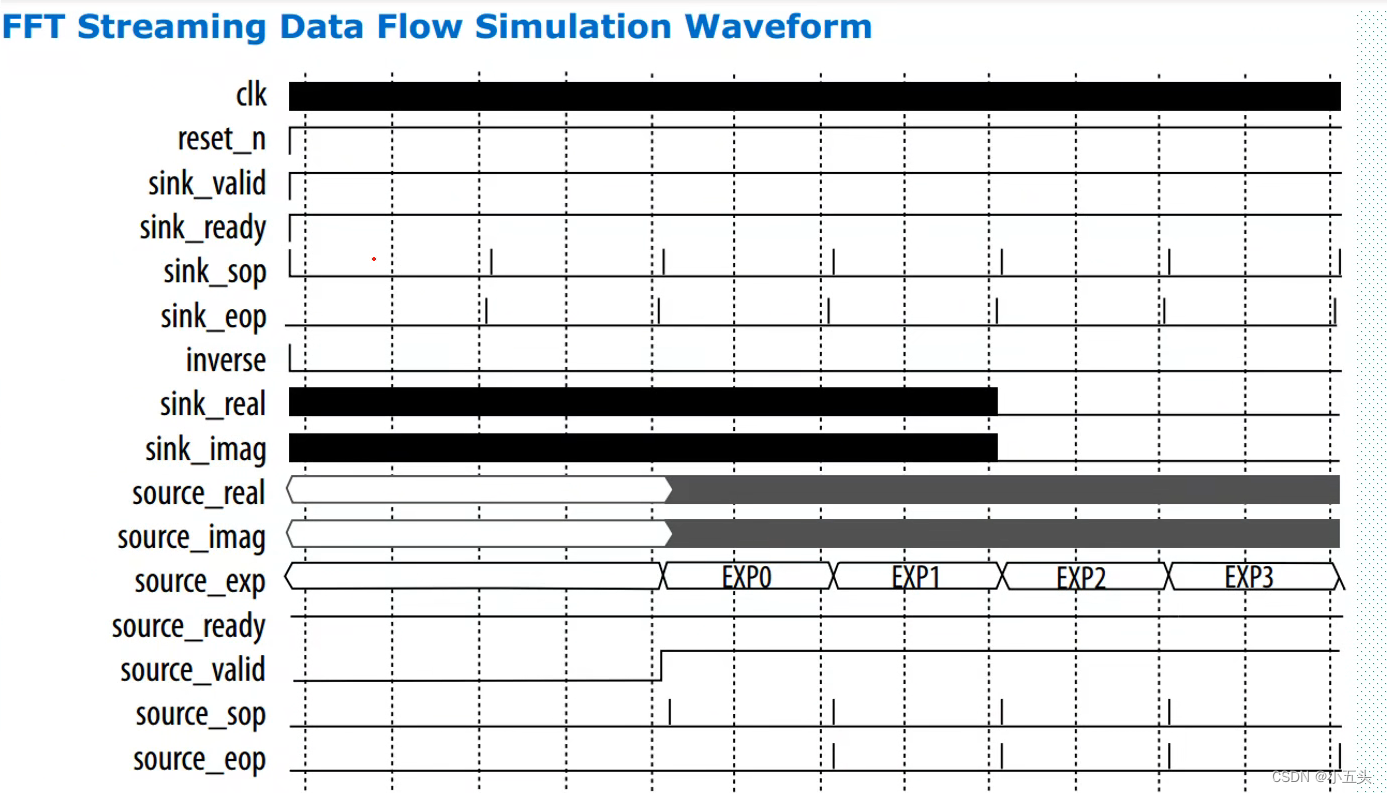

     图11.9

    IP核搭建

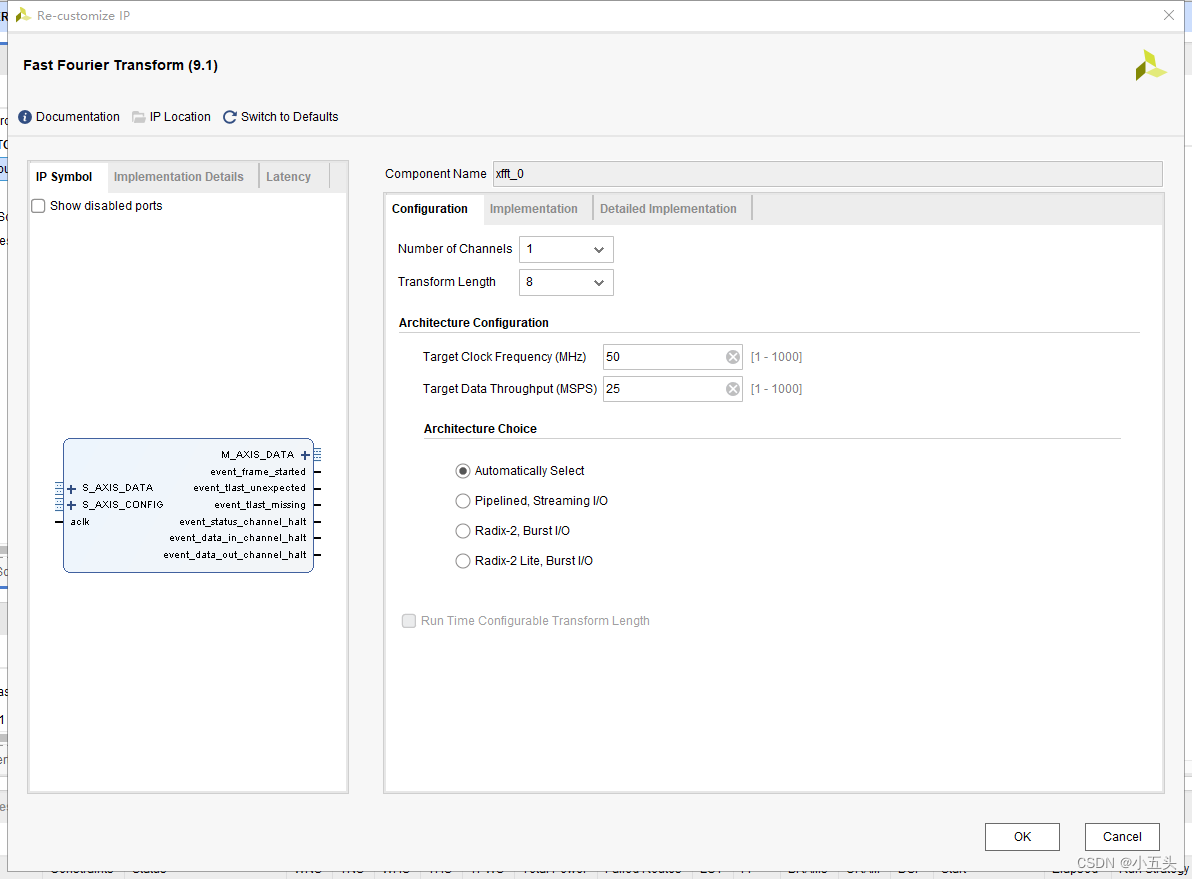
第一个选项是同时进行几路数据流并行。
第二个选项是变换的实际点数，如果设计可以在线更改变换点数的FFT，这里选择的点数是所需要的最大的FFT点数。
第三个工作时钟（Target Clock Frequency）。
第四个选择一种FFT结构，包括流水线Streaming、基4 Burst、基2 Burst和轻量级基2 Burst，计算速度和消耗的资源依次减少。
第五个需要实时更改FFT的点数，则需要更改Run Time Configurable Transform Length。

Implementation标签卡下
设置FFT的数据格式为定点Fixed Point或浮点Float Point；
设置输入数据的位宽和相位因子位宽（相当于旋转因子）。
ARESETn这个信号一般要选上
“Output Ordering”设置FFT计算结果以自然顺序（Nature Order）或位/数值反序（Bit/Digit Reversed Order）输出。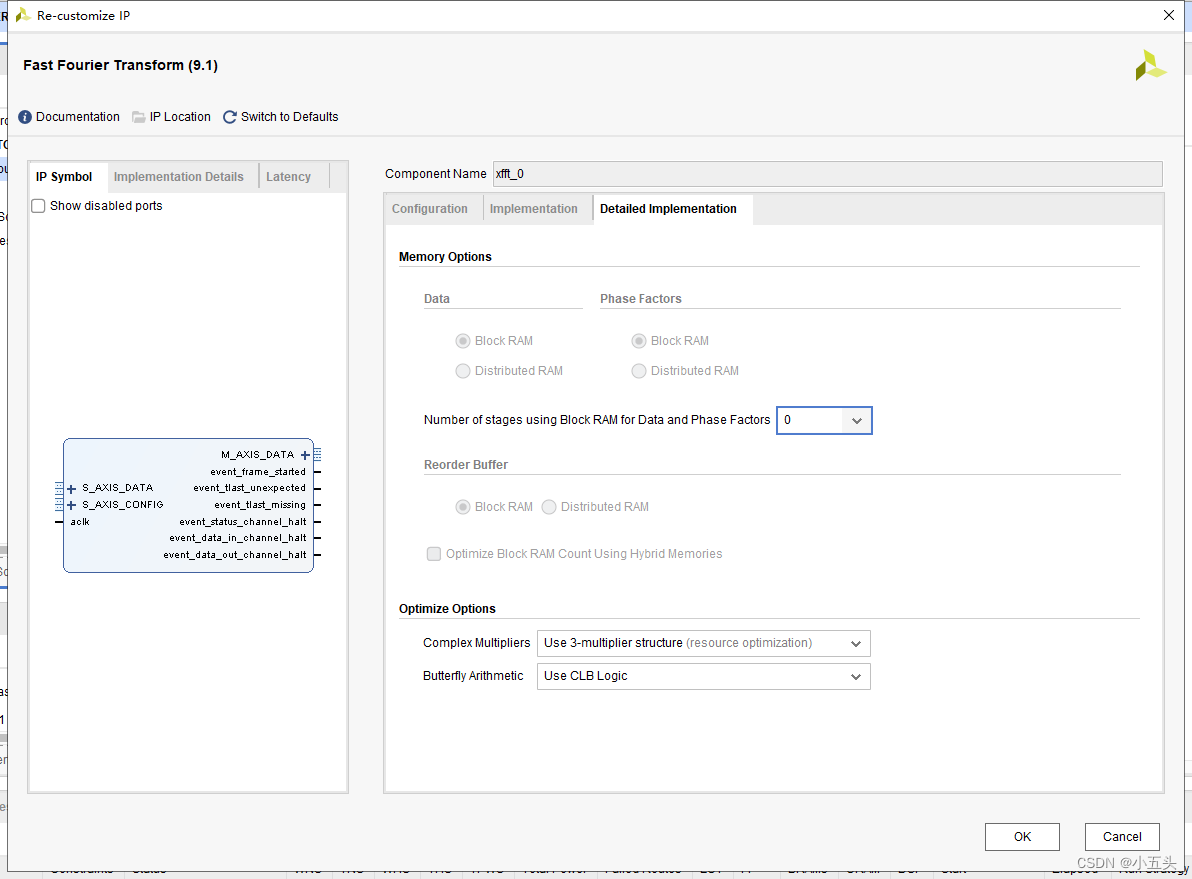

  代码编写

module FFT_TOP(
	input wire 	clk,
	input wire  rst
    );
    
  reg [3:0]     state;
  reg [10:0]    cnt;
  reg [15:0]    real_data;
  reg [15:0]    imag_data;
  reg           s_axis_data_tvalid;
  reg           s_axis_data_tlast;
  reg           s_axis_config_tvalid;
  reg           m_axis_data_tready;
  reg [7:0]     s_axis_config_tdata;

  wire s_axis_config_tready;
  wire [31:0] s_axis_data_tdata;
  wire s_axis_data_tready;
  wire [31 : 0] m_axis_data_tdata;
  wire m_axis_data_tvalid;
  wire m_axis_data_tlast;
  wire event_frame_started;
  wire event_tlast_unexpected;
  wire event_tlast_missing;
  wire event_status_channel_halt;
  wire event_data_in_channel_halt;
  wire event_data_out_channel_halt;
  wire [15:0] real_dataout;
  wire [15:0] imag_dataout;
    
  assign s_axis_data_tdata = {imag_data,real_data};
  assign real_dataout = m_axis_data_tdata[31:16];
  assign imag_dataout = m_axis_data_tdata[15:0];
    
    always @ (posedge clk ) begin 
        if (rst)
         begin 
            state       <=  4'd0;
            imag_data   <=  16'd0;
            real_data   <=  16'd0;
            s_axis_data_tvalid<=1'b0;
            cnt         <=  11'd0;
            s_axis_config_tvalid<=1'b0;
            m_axis_data_tready<=1'b0;
            s_axis_config_tdata<=8'd0;
         end 
        else 
            case (state)
                0:begin 
                        state       <=  state   +   1'b1;
                        imag_data   <=  16'd0;
                        real_data   <=  16'd0;
                        cnt         <=  11'd0;
                        s_axis_data_tvalid<=1'b0;
                        s_axis_config_tvalid<=1'b1;
                        m_axis_data_tready<=1'b1;
                        s_axis_config_tdata<=8'd1;
                end 
                1:begin 
                    if (cnt ==  1000-1)
                     begin 
                        cnt         <=  11'd0;
                        state       <=  state   +   1'b1;
                     end 
                    else 
                     begin 
                        cnt         <=  cnt +   1'b1;
                        state       <=  state;
                     end 
                end 
                2:begin real_data <= 16'h4; s_axis_data_tvalid  <=  1'b1; state <= state + 1'b1; end 
                3:begin real_data <= 16'h3; s_axis_data_tvalid  <=  1'b1; state <= state + 1'b1; end 
                4:begin real_data <= 16'h2; s_axis_data_tvalid  <=  1'b1; state <= state + 1'b1; end 
                5:begin real_data <= 16'h6; s_axis_data_tvalid  <=  1'b1; state <= state + 1'b1; end 
                6:begin real_data <= 16'h7; s_axis_data_tvalid  <=  1'b1; state <= state + 1'b1; end 
                7:begin real_data <= 16'h8; s_axis_data_tvalid  <=  1'b1; state <= state + 1'b1; end 
                8:begin real_data <= 16'h9; s_axis_data_tvalid  <=  1'b1; state <= state + 1'b1; end 
                9:begin real_data <= 16'h0; s_axis_data_tvalid  <=  1'b1; state <= state + 1'b1; end 
                10:begin 
                s_axis_data_tvalid<=1'b0;
                real_data<=16'd0;
                state<=state;
                end 
                default : ;
               endcase 
    end 
    always @ (posedge clk ) begin 
        if (rst)
            s_axis_data_tlast   <=  1'b0;
        else if (state  == 9)
            s_axis_data_tlast   <=  1'b1;
        else 
            s_axis_data_tlast   <=  1'b0;
       end 
    
    
xfft_0 your_instance_name (
  .aclk						(clk),                                                // input wire aclk
  //低位配置工作模式，可同时配置多通道，1为FFT，0为IFFT[7 : 0]
  .s_axis_config_tdata(s_axis_config_tdata),         
  //配置信息有效信号，无特殊要求置1即可。
  .s_axis_config_tvalid(s_axis_config_tvalid),        
  //准备接收配置信息
  .s_axis_config_tready(s_axis_config_tready),               
  // [31 : 0]输入数据（高n位为虚部信号，低n位为实部信号）
  .s_axis_data_tdata(s_axis_data_tdata),            
  //输入有效信号
  .s_axis_data_tvalid(s_axis_data_tvalid),                   
  //输出信号，代表该ip核可以进行下一次运算
  .s_axis_data_tready(s_axis_data_tready),                    
  //输入最后一个数据时拉高信号，只是为了区分数据来源，属于可选配置。
  .s_axis_data_tlast(s_axis_data_tlast),                      
  //携带BLK_EXP以及OVFLO信息，两个信息不能同时通过该输出口显示[31 : 0]
  .m_axis_data_tdata(m_axis_data_tdata),                    
  //状态信息有效信号
  .m_axis_data_tvalid(m_axis_data_tvalid),                    // output wire m_axis_data_tvalid
  //非必选，外部系统准备好接收状态信号的时候输入高电平。仅用于非实时状态。
  .m_axis_data_tready(m_axis_data_tready),                    // input wire m_axis_data_tready
  //输出数据的最后一位。
  .m_axis_data_tlast(m_axis_data_tlast),                      // output wire m_axis_data_tlast
  //拉高一个时钟周期，指示开启新的处理过程，一般用于更新配置信息。
  .event_frame_started(event_frame_started),                  // output wire event_frame_started
  //当ip核没有采集到足够点数就出现了
  .event_tlast_unexpected(event_tlast_unexpected),            // output wire event_tlast_unexpected
  //当采集的数据足够但s_axis_data_tlast未拉高时，会产生提示。
  .event_tlast_missing(event_tlast_missing),                  // output wire event_tlast_missing
  //当内核准备好输出状态数据但是无法输出。仅在非实时模式。
  .event_status_channel_halt(event_status_channel_halt),      // output wire event_status_channel_halt
  //当内核准备好接收数据但无有效数据输入时产生提示。
  .event_data_in_channel_halt(event_data_in_channel_halt),    // output wire event_data_in_channel_halt
  //当内核准备好输出数据但是无法输出。仅在非实时模式。
  .event_data_out_channel_halt(event_data_out_channel_halt)  // output wire event_data_out_channel_halt
);

endmodule

  仿真验证

        与上述实验结果相同，但是顺序不同。（问题博主查询找.............）

致谢/参考文献

1. Bracewell, R. N. (2000). The Fourier transform and its applications (3rd ed.). New York: McGraw-Hill.
2. Oppenheim, A. V., & Schafer, R. W. (2010). Discrete-time signal processing (3rd ed.). Upper Saddle River, NJ: Prentice Hall.
3. Strang, G. (1993). Introduction to Applied Mathematics. Wellesley, MA: Wellesley-Cambridge Press.
4. Proakis, J. G., & Manolakis, D. G. (2006). Digital signal processing: Principles, algorithms, and applications (4th ed.). Upper Saddle River, NJ: Prentice Hall.
5. Papoulis, A. (1977). Signal analysis. New York: McGraw-Hill
6. Fourier, J. B. J. (1822). Théorie analytique de la chaleur.
7. Shannon, C. E. (1949). Communication in the presence of noise.
8. Cooley, J., & Tukey, J. (1965). An algorithm for the machine calculation of complex Fourier series.
9. Oppenheim, A. V., & Schafer, R.W. (1968). Digital signal analysis.
10. Mallat, S. G. (1989). A theory for multiresolution signal decomposition: The wavelet representation.

11. https://blog.csdn.net/weixin_41920053/article/details/104618551

    https://www.cnblogs.com/limanjihe/p/9999526.html

    https://blog.csdn.net/CLL_caicai/article/details/107022319

    https://blog.csdn.net/weixin_42837669/article/details/118496144

    https://blog.csdn.net/weixin_40640020/article/details/85006846

    https://zhuanlan.zhihu.com/p/134150702

    https://blog.csdn.net/beauytlife_1985/article/details/82115522

    https://blog.csdn.net/a18271623106/article/details/115752709

12. 一小时学会快速傅里叶变换_哔哩哔哩_bilibili

13. Mark Newman - YouTube